IZLASH ALGORITMLARI. KNUT VA MORE ALGORITMLARI







![Izlash algoritmlari
Satrlardan qismiy satrni qidirish algoritmi – bu matnda (text) qismiy satr
(pattern) topishga imkon beradigan satrlar ustidagi algoritmlar sinfi. U matn
muharrirlari, MBBT, qidiruv tizimlari, dasturlash tillari va boshqalarda o'rnatilgan
funksiya sifatida ishlatiladi.
Qidiruv vazifalarida qidiruv satrni “igna” (inglizchadan - "needle") va
qidiruv o'tkaziladigan satrni “g’aram” (ingliz tilidan - "haystack") deb belgilash
odat tusiga kirgan. Shuningdek, biz qidirish olib boriladigan alifboni Σ bilan
belgilaymiz.
Primitiv algoritmning muvaffaqiyatsizligi. Agar satrlar birdan boshlab
raqamlangan deb hisoblasak, eng oddiy “qo'pol kuch” (Brute force) algoritmi
(sodda algoritm) quyidagicha bo’ladi:
for i=0...|haystack|-|needle|
for j=0...|needle|
if haystack[i+j + 1]<>needle[j]
then goto 1
output("Topildi: ", i+1)
1:
Eng oddiy qidirish algoritmi, eng yaxshisi, |haystack| - |needle| +1
taqqoslash; agar bir-biriga o'xshashliklar ko'p bo'lsa, tezlik O(|haystack|·|needle|)
ga tushadi.
Primitiv algoritm o'rtacha 2 soatlik taqqoslashda ishlayotgani isbotlangan.
Bugungi kunda qismiy satrlarni qidirish algoritmlarining xilma-xilligi
mavjud. Dasturchi bunday omillarga qarab, mosini tanlashi kerak.
1. Optimallashtirish kerakmi yoki primitiv algoritm yetarlimi? Jimlik
bo’yicha, bu dasturlash tillarining standart kutubxonalari amalga oshiradi.
2. Foydalanuvchining "dushmanligi". Boshqacha aytganda:
foydalanuvchi ataylab algoritm sekin bajariladigan ma'lumotlarni
aniqlaydimi? Eng oddiy holatda O (| haystack | · | needle|) ball qo'yadigan
juda oddiy algoritmlar mavjud, lekin "muntazam" ma'lumotlarda
solishtirishlar soni | haystack | dan ancha kam. Faqat 1990-yillarda O (|
haystack |) ning murakkabligini, eng yomon holatda va | haystack |
o'rtacha.
3. Tilning grammatikasi qidiruvni "o'rtacha" tezlashtiradigan ba'zi
evristikalarga dushman bo'lishi mumkin.
4. Protsessor arxitekturasi. Ba'zi protsessorlarda avtomatik kattalashtirish
yoki SIMD amallari mavjud bo'lib, ular sizga ikkita operativ xotirani tez
taqqoslashga imkon beradi (masalan, x86-da rep cmpsd). Bunday
protsessorlarda “needle”ni “haystack” bilan taqqoslaydigan algoritmni
qo'llash juda qiziq - albatta, hamma pozitsiyalarda emas.
5. Alifbo o'lchami. Ko'p algoritmlar (ayniqsa, oxirigacha taqqoslashga
asoslangan), mos kelmaydigan belgi bilan bog'liq evristikaga ega. Katta
8](/data/documents/beb0c01f-05eb-447e-8ed8-556f2190f887/page_8.png)


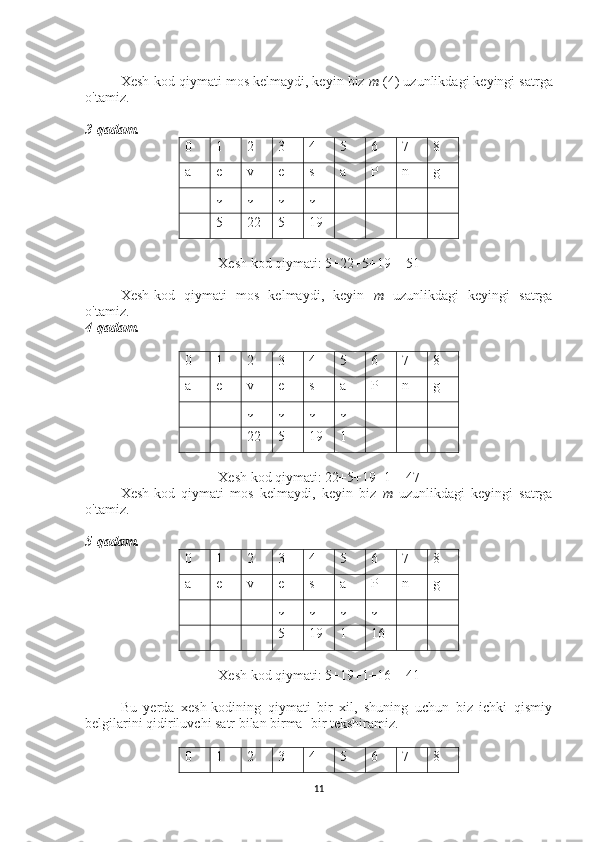

![void rabin_karp ( string &text,string &pattern, int q )
{
/*qismiy satr uzunligi*/
int m = pattern.length () ;
/*Berilgan satr uzunligi*/
int n = text.length () ;
int p=0,t=0,h=1,d=26; // bu yerda p - matn uchun xesh qiymati, t – qismiy
satrning xesh qiymati;
/*h=pow(d,M-1) bu yerda d - 26, agar matnda faqat katta harflar bo'lsa.*/
for ( int i=0;i < m-1;i++ )
{
h= ( h*d ) %q;
}
/* matn va m uzunligining birinchi ichki satri uchun xesh qiymatini
hisoblash */
for ( int i=0;i < m;i++ )
{
p= ( d*p+pattern [ i ]) %q;;
t= ( d*t+text [ i ]) %q;
}
/* m uzunlikdagi qolgan satr uchun */
for ( int i=0;i < =n-m;i++ )
{
/* agar xesh qiymatlari bir xil bo'lsa, xeshni ichki satr va qismiy satridagi
belgilar bo'yicha tekshirish */
if ( p==t )
{
int flag=0;
for ( int j=0;j < m;j++ )
{
if ( text [ i+j ] !=pattern [ j ])
{
flag=1;
break;
}
}
/* agar barcha belgilar mos keladigan bo'lsa, ichki satrning boshlang'ich
indeksini chop etish.*/
if ( flag==0 )
{
cout << " Indeksda berilgan satr osti topildi:" << i+1 << endl;
}
}
13](/data/documents/beb0c01f-05eb-447e-8ed8-556f2190f887/page_13.png)
![/*oldingi ichki satrdan birinchi belgini olib tashlash orqali keyingi ichki
satrning xesh qiymatini toping va keyingi satrni oldingi satr oxiriga
qo'shing*/
/*xesh qiymatlarini topish uchun O (1) vaqt kerak bo'ladi*/
if ( i < n-m )
{
t= ( d* ( t-text [ i ] *h ) +text [ i+m ]) %q;
if ( t < 0 )
{
t= ( t+q ) ;
}
}
}
}
int main ()
{
/*o’zgaruvchilarni kiritish*/
string text;
cin >> text;
string pattern;
cin >> pattern;
rabin_karp ( text,pattern,97 ) ;
return 0;
}
Boyer-Mur algoritmi. 1977-yilda Robert Boyer va Jey Mur tomonidan
ishlab chiqilgan, matnda oldindan ishlov berish imkoniyati bo'lmagan taqdirda,
satrda qismiy satrni topish algoritmlari orasida eng tezkori hisoblanadi .
Algoritm g'oyasi quyidagicha:
- Chapdan o'ngga skanerlash, o'ngdan chapga taqqoslash.
- To'xtash belgisini topish
o agar taqqoslanadigan birinchi harf mos kelmasa, shablon eng yaqiniga
o'tkaziladi
o to'xtash belgisi bo'lmasa, shablon uning orqasiga siljiydi
- Mos keladigan qo'shimchani topish
o agar 1 yoki undan ortiq belgi mos kelsa, shablon bu qo'shimchaning
birinchi mos kelishiga qadar o'ngga siljiydi
1. q w t e e q e w q r w q w r q r
q w r q r
14](/data/documents/beb0c01f-05eb-447e-8ed8-556f2190f887/page_14.png)

![1991-yilda Koul shuni ko'rsatdiki, davriy bo'lmagan sxemalar bo'yicha,
algoritm satr bo'ylab to'liq o'tishda 3·|haystack| tadan ko'p bo'lmagan taqqoslashni
amalga oshiradi.
Boyer-Mura algoritmi (C++)
#include <bits/stdc++.h>
using namespace std;
# define NO_OF_CHARS 256
void badCharHeuristic( string str, int size, int badchar[NO_OF_CHARS])
{
int i;
for (i = 0; i < NO_OF_CHARS; i++)
badchar[i] = -1;
for (i = 0; i < size; i++)
badchar[(int) str[i]] = i;
}
void search( string txt, string pat)
{
int m = pat.size();
int n = txt.size();
int badchar[NO_OF_CHARS];
badCharHeuristic(pat, m, badchar);
int s = 0;
while(s <= (n - m))
{
int j = m - 1;
while(j >= 0 && pat[j] == txt[s + j])
j--;
if (j < 0)
{
cout << s << endl;
s += (s + m < n)? m-badchar[txt[s + m]] : 1;
}
else
s += max(1, j - badchar[txt[s + j]]);
}
16](/data/documents/beb0c01f-05eb-447e-8ed8-556f2190f887/page_16.png)
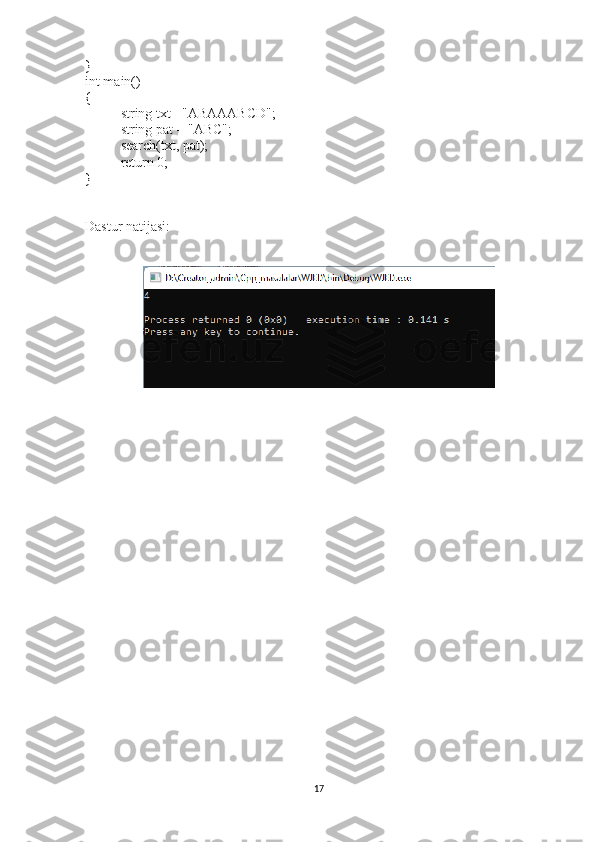

![// satrdagi naqsh boshi indeksini qaytaradi, topilmasa -1
int find (char * namuna, char * string1)
{
// i- biz qidirayotgan qatorning qayerida
// j-namunaning qaysi joyidan izlayapmiz
for (int i=0; string1 [i];++i) {
for (int j=0;;++j) {
if (!namuna [j]) return i;
if(string1[i+j]!=namuna [j]) break;
}
// hali topilmadi, tashqi sikl bilan davom eting
}
// namuna yo'q
return -1;
}
Funktsiya ishlaydi va agar namunalar va satr "yaxshi" bo'lsa, juda tez ishlaydi.
Yaxshi bo'lganlar, ichki pastadir tezda uzilib qolganda (1-3 qadamda, aytaylik,
oddiy holatda bo'lgani kabi). Ammo agar naqsh va satr tez-tez takrorlanadigan
ichki qismlarni o'z ichiga olsa (yuqoridagi murakkab holatda bo'lgani kabi), u
holda ichki halqa naqsh oxiriga kelib uziladi va qidiruv vaqti O (<naqsh uzunligi>
* <string uzunligi) sifatida baholanadi. >). Agar ipning uzunligi 100 ming, namuna
uzunligi 100 bo'lsa, biz O (10 million) ni olamiz. Albatta, aslida siz 100
uzunlikdagi naqshni kamdan-kam uchratasiz, ammo olimpiada muammolarida
"qidirish uchun" bu odatiy holdir, shuning uchun oddiy qidiruv ko'pincha mos
kelmaydi. , va siz yozayotganda tezda. so'z (brauzerlar buni qanchalik tez
bajarayotganini payqadingizmi)? KMP algoritmi satrda naqshning barcha paydo
bo'lishini va uning tezligini O (<naqsh uzunligi> + <string uzunligi>) topadi,
shuning uchun katta matnlarda / namunalarda yoki zaif protsessorlarda (past
budjetli uyali telefonlar kabi) bu raqobatdan tashqari.Endi sarlavhaga qaraylik?
Nima uchun "kichik"? Chunki KMP ning diqqatga sazovor joyi prefiks
19](/data/documents/beb0c01f-05eb-447e-8ed8-556f2190f887/page_19.png)
![funktsiyasidir va u haqiqatan ham kichikdir. Nega "mo''jiza"? Chunki u butunlay
boshqa masalani yechayotgandek tuyuladi va bu yechim qandaydir ajoyib hiyladan
so‘ng satrda naqshning barcha ko‘rinishlarini topish masalasining yechimiga
aylanadi.Prefiks funksiyasi nima va qanday ishlashini tushunish uchun ko‘rib
chiqamiz. murakkab qatorda
a a b a a b a a a a b a a b а a a b
1 2 3 4 5 6 7 8 9 1
0 1
1 1
2 1
3 1
4 1
5 1
6 1
7 1
8
0 1 0 1 2 3 4 5 2 2 3 4 5 6 7 8 9 3
Uning ostidagi chiziq satrdagi belgining raqami (pozitsiyasi) (algoritmni tavsiflash
qulayligi uchun biz raqamni 1 dan hisoblaymiz), pastki qator esa M prefiks
uzunliklari massivi bo'lib, uni tushunish kalitidir. prefiks funktsiyasi. 7 raqamiga
ega bo'lgan belgini oling (bu a) va 1 dan 6 gacha bo'lgan K uchun prefiks satrlarni
(satrning birinchi indeksidan boshlanadigan pastki qator) va qo'shimchalarni
(pastki satr, oxirgi belgisini ko'rib chiqing). 7-pozitsiyadagi satr (bu "bizning" a
belgisi) uzunligi K.
Endi yana bir holat - P8 kengaytirilmadi, ya'ni. S [9] = a belgisi M [8] + 1 = 6 b
pozitsiyasidagi S qatorning belgisiga mos kelmadi. Qo'shimcha osongina
kengayadi (chunki yangi belgi oxiriga qo'shiladi), lekin muammoli prefiks bilan,
chunki qo'shimchasiga qo'shilgan belgi keyingi prefiks belgisiga mos kelmasligi
mumkin. Agar P (k) prefiksi mos kelmasa, siz bir xil qo'shimchaga ega bo'lgan
qisqaroq boshqa prefiksni topishingiz va uni kengaytirishga harakat qilishingiz
kerak. Ammo prefiks qisqaroq va xuddi shu qo'shimcha bilan u S [M [M [k]],
chunki M massivni to'ldirishda har bir element bir xil qo'shimchali eng uzun
20](/data/documents/beb0c01f-05eb-447e-8ed8-556f2190f887/page_20.png)
![prefiksning uzunligini o'z ichiga oladi. Shuning uchun, agar S (M [k]) ni
kengaytirishning iloji bo'lmasa, S (M [M [k]]) va boshqalarni mos kelguncha yoki
biz nolga teng bo'lgunga qadar kengaytirishga harakat qiling (keyin keyingi belgi S
shunchaki. S satrning 1-belgisi bilan solishtirish kerak). Tegishli prefikslarni
qidirish tsikli juda tez tugaydi, chunki buning uchun zarur bo'lgan barcha
ma'lumotlar allaqachon M massivida. Bizning P (8) qatorimiz P (7) ning bir belgi
bilan kengaytmasi bo'lib, 1 ta taqqoslash kerak bo'ldi. Biroq, P (8) ni P (9) ga
kengaytirib bo'lmadi, chunki S [9] = a va S [M [8] + 1 = 6] = b. M [8] = 5
uzunlikdagi P8 prefiksi mos kelmaganligi sababli, M [5] = 2 uzunlikdagi prefiksni
sinab ko'ring. U ham mos kelmaydi: S [2 + 1] = b. Biz M [2] = 1 uzunlikdagi
prefiksni sinab ko'ramiz va uni uzaytirish mumkin, chunki S [1 + 1] = a. Shuning
uchun, M [9] = 2, kengaytirilgan prefiksning uzunligidan biriga ko'proq. M [10] ni
to'ldirish uchun sizga 2 ta taqqoslash kerak (tekshirishingiz mumkin). Ammo 11
dan 17 gacha bo'lgan elementlarni to'ldirish uchun sizga bitta taqqoslash kerak.
Natijada, massiv qiymatlarini hisoblash O tartibidagi vaqtni oladi (satr uzunligi)
Shunday qilib, to'ldirish algoritmi ko'proq yoki kamroq aniq.
Keling, hiyla-nayrangga o'tamiz.
aabaabaaaabaabaaab qatorida aabaa naqshini topish uchun naqshni shunday
chiziqqa yopishtiring aabaa @ aabaabaaaaaaabaaab va massivni to'ldirish uchun
prefiks funksiyasini chaqiring.
21](/data/documents/beb0c01f-05eb-447e-8ed8-556f2190f887/page_21.png)
 mutable
{
i++;
if (i <= n)
{
sample.push_back(item);
}
else if (std::rand() % i < n)
{
sample[std::rand() % n] = item;
}
22](/data/documents/beb0c01f-05eb-447e-8ed8-556f2190f887/page_22.png)
![return sample;
};
}
int main() {
std::srand(std::time(NULL));
int bin[10] = {0};
for (int trial = 0; trial < 100000; trial++)
{
auto s_of_n = s_of_n_creator<int>(3);
std::vector<int> sample;
for (int i = 0; i < 10; i++)
sample = s_of_n(i);
for (int s : sample)
bin[s]++;
}
for (int x : bin)
std::cout << x << std::endl;
return 0;
}
23](/data/documents/beb0c01f-05eb-447e-8ed8-556f2190f887/page_23.png)



“IZLASH ALGORITMLARI. KNUT VA MORE ALGORITMLARI” Reja: Kirish Asosiy qism: 1. Algoritm tushuchasi 2. Izlash algoritmlari 3. Knut va More algoritmlari Xulosa Foydalanilgan adabiyotlar Foydalanilgan internet saytlar
KIRISH Avvalo algoritm tushunchasi IX asrlarda yashab ijod etgan buyuk bobokalonimiz Muhammad al-Xorazmiy nomi bilan uzviy bog’liqligini tushuntirish lozim. Algoritm so’zi al-Xorazmiyning arifmetikaga bag’ishlangan asarining dastlabki betidagi “Dixit Algoritmi” (“dediki al-Xorazmiy” ning lotincha ifodasi) degan jumlalardan kelib chiqqan. Shundan so’ng al-Xorazmiyning sanoq sistemasini takomillashtirishga qo’shgan hissasi, uning asarlari algoritm tushunchasining kiritilishiga sabab bo’lganligi ta’kidlab o’tiladi. Algoritm nima degan savolga, u asosiy tushuncha sifatida qabul qilinganligidan, uning faqat tavsifi beriladi, ya’ni biror maqsadga erishishga yoki qandaydir masalani yechishga qaratilgan ko’rsatmalarning (buyruqlarning) aniq, tushunarli, chekli hamda to’liq tizimi tushuniladi. Algoritm tushunchasi aniq shaklda XX-asr boshlarida D. Gilbert, K. Gyodel, S. Klin, A. Chyorch, E. Post, A. Tyuring, N. Viner, A. A. Markov singari olimlarning asarlari tufayli shakllandi. Eng qadimiy raqamli algoritmlardan biri Yevklid algoritmi (miloddan avvalgi III asr) deb hisoblanadi - ikki sonning eng katta umumiy bo'luvchisini topish. Algoritmlarning zamonaviy nazariyasi nemis matematikasi Kurt Gyodel (1931) asarlari bilan boshlandi, ular o'zlarining rasmiy, izchil aksiomalar tizimi doirasida yechib bo'lmaydigan muammolar mavjudligini ko'rsatdi. 2
Algoritm tushunchasi Algoritm – berilgan natijaga erishish uchun qilinishi kerak bo lgan aniqʻ ko rsatmalar ketma-ketligi. ʻ Algoritm keng ma noda faqat kompyuterga oid atama ʼ bo lmay, balki unda berilgan ko rsatmalarni bajara oluvchi har qanday narsaga ʻ ʻ oiddir. Algoritm — ma lum bir turga oid masalalarni yechishda ishlatiladigan ʼ amallarning muayyan tartibda bajarilishi haqidagi aniq qoida (dastur). Kibernetika va matematikaning asosiy tushunchalaridan biri. Algoritm so’zi Al – Xorazmiy nomining lotincha talaffuzidan kelib chiqqan bo’lib. Muxammad Muso Al-Xorazmiyning X asrda yaratilgan qo’llanmasida keltirilgan o’nlik sanoq sistemasida arifmetik amallarni bajarish qoidalari soddaligi tufayli yevropada ham o’nlik sanoq sistemasi qo’llanishiga turtki bo’ldi. Bu qoidalar tarjimasida xar bir qoida “ Al-Xorazmiy aytadiki ” deb boshlangan va bora-bora talaffuz tufayli algoritm tarzida ifodalanib kelgan. Hozirgi paytda algoritm sifatida biror masalani ishlash yoki biror ishni bajarish uchun qilinishi kerak bo’lgan tartiblangan chekli sondagi aniq bir qiymatli ko’rsatmalar ketma-ketligi tushiniladi. Algoritm tushunchasi keng ma’noda tahlil qilish mumkin. Masalan, biror manzildan boshqa manzilga borish uchun shahar transportidan foydalanib qanday borish mumkin, degan savolga biz ma’lum algoritm tavsiya qilishimiz mumkin. Pazandalik kitobida, masalan, palovni pishirish qoidasi keltiriladi. Bu ham o’ziga xos algoritm hisoblashlar ishlanadigan masala algoritmini biz hisoblash algoritmi deymiz. Biz asosan hisoblash algoritmlari haqida so’z yuritamiz. Algoritmlarga xos bo’lgan belgi va talablarni sanab o’tamiz. Har qanday algoritm quyidagi asosiy xususiyatlarga ega bo’lishi kerak: 3
Determinantlik sifati Berilgan boshlangich qiymatlarda bir qiymatli javob olinishi; Ommaviylik sifati Ma’lum turdagi masalalar uchun turli boshlangich qiymatlarda yechim olish mumkin bo’lishi; Diskretlilik sifati Algoritmni EHM(Elektron Hisoblash Mashinalari) yoki inson tomonidan bajarilishi mumkinligi shubxasiz bo’lgan ayrim-ayrim sodda bosqichlarga bo’lish mumkinligi. Natijaviylik sifati Har qanday boshlangich qiymatlarda ham javobning mavjudligi, bunda «bu holda yechim yo’q» singari axborot ham algoritmning ishlash natijasi deb qabul qilinadi; Keltirilgan sifatlardan kelib chiqqan xolda algoritmni ifodalash va bajarish qoidalari xaqida so’z yuritish mumkin. Amaliyotda algoritmni ifodalashning uchta asosiy usullari fodalaniladi. Bular matnli ko’rinishi, sxematik(grafik) ko’rinishi, biror algoritmik tildagi (dasturiy) ifodasi. Algoritm so’zlar, matematik formulalar, algoritmik tillar, geometrik tarhlar (sxemalar), dasturlash tillari va boshqalar yordamida tavsiflanadi. Algoritmning so’zlar yordamida berilishiga, tavsiflanishiga misol tariqasida liftda kerakli qavatga ko’tarilish algoritmini keltirish mumkin. Bu quyidagicha ketma- ketlikda bajariladi: 1. Liftga kiring. 2. Kerakli-qavat tartib soniga mos tugmachani bosing. 3. Liftni harakatga keltiring. 4. Lift to’xtashini kuting. 5. Lift eshigi ochilgandan keyin undan chiqing. Algoritm matematik formulalar yordamida tavsiflanganda har bir qadam aniq formulalar yordamida yoziladi. Misol tariqasida 4
kvadrat tenglama yechimlari bo’lmish x1 x2 ni aniqlash algoritmini ko’rib chiqaylik. 1. a, b, с koeffitsiyentlar qiymatlari berilsin. 2. D = b2—4ac diskriminant hisoblansin. 3. D < 0 bo’lsa, tenglamaning haqiqiy yechimlari yo’q. Faqat haqiqiy ildizlar izlanayotgan bo’lsa, masala hal bo’ldi. 4. D = 0 bo’lsa, tenglama ikkita bir-biriga teng, ya’ni karrali yechimga ega bo’ladi va ular formulalar bilan hi-soblanadi. Masala hal bo’ldi. 5. D > 0 bo’lsa, tenglama ikkita haqiqiy yechimga ega, ular formulalar bilan hisoblanadi. Ya’ni masala hal bo’ldi. Shunday qilib, kvadrat tenglamaning haqiqiy yechim-larini aniqlashda: 1. «Tenglamaning haqiqiy yechimlari yo’q» matm 2. «Tenglama karrali yechimga ega, x=x2 matni va x1, x2 ning qiymatlari; 3. «Tenglama ikkita yechimga ega» matni, xx va x2 ning qiymatlari natijalar bo’ladi. Algoritmik tillar — algoritmni bir ma’noli tavsiflash imkonini beradigan belgilar va qoidalar majmuidir. Har qanday tillardagidek ular ham o’z alifbosi, sintaksisi va semantikasi bilan aniqlanadi. Bizga o’rta maktabdan ma’lum bo’lgan ( akademik A. P. Yershov rahbarligida yaratilgan ) EHMsiz algoritmlashga mo’ljallangan algoritmik tizim algoritmik tilning namunasidir. Algoritmik tilga misol sifatida yana algoritmlarni belgili operatorlar tizimi shaklida tavsiflashni ham ko’rsatish mumkin. Bu tillar odatdagi tilga o’xshash bo’lib, EHMda bevosita bajarishga mo’ljallanmagan. Ulardan maqsad algoritmni bir xil shaklda va tushunarli qilib, tahlil qilishga oson qilib yozishdir. Algoritmlarni geometrik tarhlar yordamida tavsiflash ko’rgazmali va, shu sababli tushunarliroq bo’lgani uchun ko’p qo’llaniladi. Bunda har bir o’ziga xos operatsiya alohida geometrik shakl (blok) bilan tavsiflanadi va ularning bajarilish tartibi, ular orasidagi ma’lumotlar uzatilishi va yo’nalishi bloklarni bir-biri bilan ko’rsatkichli to’g’ri chiziqlar yordamida tutashtirib ko’rsatiladi. Algoritmning geometrik tarhiga uning bloktarhi (blok-sxemasi) deyiladi. Bloklarga mos geometrik shakllar, ularning o’lchamlari va ular yordamida bloktarhlarni chizish qoidalari davlat standartlarida berilgan. 1-jadvalda eng ko’p ishlatiladigan bloklar shakli va ularning ma’nosi keltirilgan. Bu davlat standartlariga ko’ra bloklarni tutashtiruvchi to’g’ri chiziq yozuv tekisligiga vertikal yoki gorizontal holatda bo’lishi kerak, ya’ni ularni og’ma chiziqlar bilan tutashtirish taqiqlanadi. Bloklarni bajarish tabiiy yozish tartibida bo’lsa, ya’ni yuqoridan pastga yoki chapdan o’ngga bo’lsa, tutashtiruvchi chiziq ko’rsatkichsiz bo’lishi mumkin. 5
