logo
  1. Главная страница
  2. Дипломные работы
  3. Общий
  4. Shell saralash algortmi

Shell saralash algortmi

Загружено в:

23.11.2024

Скачано:

0

Размер:

173.0302734375 KB
Скачать
Mavzu : Shell saralash al gortmi Reja : I.Kirish II.Asosiy qism 1.Shell saralash algortmi. 2. Algoritmning tahlili. 3. Tez saralash algoritmining tahlili. III Xulosa IV Foydalanilgan adabiyotlar KIRISH Saralash tushunchasi Saralash - tartiblash (Sorting algorithms) deb, berilgan obyektlar ketma-ketligini malum mantiqiy tartibda qayta joylashtirish jarayoniga aytiladi. Saralash bir nechta ko'rsatkichlarga bog'liq bo'lishi mumkin. Misol uvhun maktab jurnalida o'quvchilar familiyasi alifbo tartibiga ko'ra saralangan bo'ladi. Masalan bizga sonlar qatori berilgan: 8,23,0,-50,100 bu qatorni kichigidan kattasiga qarab yoki kattasidan kichigiga qarab saralashishimiz mumkin. Bu saralashni amalga oshirish jarayoni Saralash algoritmi deyiladi Saralash algoritmlari ko'p va xilma-xil. Saralash algoritmlari ikki tipga bo'linadi. - O() vatda saralovchi algoritmlar. Yani kvadratik amallar talab qiladigan algoritmlar - O(n*log(N)) vaqtda saralovchi algoritmlar. Logarifmik amallar soni talab qiladigan algoritmlar Saralash algoritmi va turlari - Bubble sort (Pufakchali saralash) - Selection sort (Tanlab saralash) - Insertion sort (Joylashtirib saralash) - Quick sort (Tezkor saralash) - Merge sort (Qo'shib saralash) Bubble sort Bu eng sodda, ketma-ketlikdagi har bir sonni boshqa sonlar bilan solishtirishga asoslangan algoritm hisoblanadi. Unda yonma-yon turgan elementlardan chapdagisi o‘ngdagidan kattaligi aniqlansa, bu ikkala son o rni almashtiriladi. Bu ʻ jarayon almashtirish kerak bo lmay qolguncha davom etadi, ya ni barcha ʻ ʼ elementlar o‘sish tartibida bo‘lib qolguncha. Algoritmi va dasturi public class BubbleSort { public static void main(String[] args) { int[] massiv = { 4, 2, 9, 6, 23, 12, 34, 0, 1 }; int n = massiv.length; int k; for (int m = n; m &gt;= 0; m--) { for (int i = 0; i &lt; n - 1; i++) { k = i + 1; if (massiv[i] &gt; massiv[k]) { int temp; temp = massiv[i]; massiv[i] = massiv[k]; massiv[k] = temp; } } for (int i = 0; i &lt; massiv.length; i++) { System.out.print(massiv[i] + ", "); } System.out.println(„\n“); } } } Chiqariluvchi natijamiz esa: 2, 4, 6, 9, 12, 23, 0, 1, 34, // 1-qadam. 2, 4, 6, 9, 12, 0, 1, 23, 34, //2-qadam. 2, 4, 6, 9, 0, 1, 12, 23, 34,//3-qadam. 2, 4, 6, 0, 1, 9, 12, 23, 34,//4-qadam. 2, 4, 0, 1, 6, 9, 12, 23, 34,//5-qadam. 2, 0, 1, 4, 6, 9, 12, 23, 34,//6-qadam. 0, 1, 2, 4, 6, 9, 12, 23, 34, //7-qadam. 0, 1, 2, 4, 6, 9, 12, 23, 34, //8-qadam. 0, 1, 2, 4, 6, 9, 12, 23, 34,//9-qadam. 0, 1, 2, 4, 6, 9, 12, 23, 34, // saralangan holdagi massiv. Selection sort Tanlab saralash bu — oddiy tartiblash algoritmidir. Ushbu tartiblash algoritmi o z ʻ joyida taqqoslashga asoslangan algoritm bo lib, unda ro yxat ikki qismga ʻ ʻ bo linadi, tartiblangan qism chap tomonda va tartiblanmagan qism o ng tomonda. ʻ ʻ Dastlab, tartiblangan qism bo sh, tartiblanmagan qismi esa butun ro yxatdir. ʻ ʻ Eng kichik element tartiblanmagan massivdan tanlanadi va eng chap element bilan almashtiriladi va bu element tartiblangan massivning bir qismiga aylanadi. Bu jarayon tartiblanmagan massiv chegarasini bitta element bilan o ngga siljitishda ʻ davom etadi. Ushbu algoritm katta ma lumotlar to plamlari uchun mos emas, chunki uning ʼ ʻ o rtacha va eng yomon holatlari murakkabligi n (n), bu yerda n ʻ — elementlar soni. Ishlash printsipi. Misol tariqasida quyidagi massivni ko rib chiqamiz: arr[] = {64, 25, 12, 22, 11} ʻ Birinchi o tish: ʻ Saralangan massivdagi birinchi o rin uchun butun massiv 0 dan 4 gacha bo lgan ʻ ʻ indeksdan ketma-ket o tkaziladi. Hozirgi vaqtda 64 saqlanadigan birinchi ʻ pozitsiya, butun massivni aylanib o tgandan so ng, 11 eng past qiymat ekanligi ʻ ʻ ayon bo ladi. ʻ Shunday qilib, 64 ni 11 bilan almashtiring. Bir iteratsiyadan so ng massivdagi eng ʻ kam qiymat bo lgan 11 , tartiblangan ro yxatning birinchi pozitsiyasida paydo ʻ ʻ bo ladi. ʻ Ikkinchi o tish: ʻ 25 mavjud bo lgan ikkinchi pozitsiya uchun massivning qolgan qismini yana ʻ ketma-ketlikda aylantiring. Ketishdan so ng biz 12 massivdagi ikkinchi eng past qiymat ekanligini va u ʻ massivda ikkinchi o rinda paydo bo lishi kerakligini aniqladik, shuning uchun bu ʻ ʻ qiymatlarni almashtiring. Uchinchi o tish: ʻ Endi, uchinchi o rin uchun, 25 mavjud bo lgan joyda yana massivning qolgan ʻ ʻ qismini aylanib o ting va massivdagi uchinchi eng kam qiymatni toping. ʻ Ketish paytida 22 uchinchi eng kam qiymat bo lib chiqdi va u massivda uchinchi ʻ o rinda paydo bo lishi kerak, shuning uchun 22 ni uchinchi o rindagi element bilan ʻ ʻ ʻ almashtiring. To rtinchi o tish: ʻ ʻ Xuddi shunday, to rtinchi pozitsiya uchun massivning qolgan qismini kesib o ting ʻ ʻ va massivdagi to rtinchi eng kichik elementni toping. ʻ 25 4-eng past qiymat bo lgani uchun u to rtinchi o rinni egallaydi. ʻ ʻ ʻ Beshinchi o tish: ʻ Nihoyat, massivda mavjud bo lgan eng katta qiymat avtomatik ravishda ʻ massivning oxirgi pozitsiyasiga joylashtiriladi Olingan massiv tartiblangan massivdir. Insertion sort (Joylab saralash) ham tartibsiz massiv elementlarini saralash uchun mo ljallangan. Uning ishlash algoritmi xuddi qo ldagi kartani saralashga o xshab ʻ ʻ ʻ ketadi. Tartibsiz turgan kartalar ichidan birini olasiz va uni o zi turishi kerak ʻ bo lgan joyga joylashtirib qo yasiz. ʻ ʻ Insertion sort ham shu ko rinishda ishlaydi. Algoritm oldin massiv boshidagi ikkita ʻ elementni saralab olib, massivning qolgan elementlarini shunga qarab o z o rniga ʻ ʻ joylashtirib chiqadi. Joylab saralash algoritmining ishlashi Misolni ko rib chiqing: arr[]: {12, 11, 13, 5, 6} ʻ Birinchi o tish ʻ Dastlab, massivning dastlabki ikkita elementi joylash tartibida taqqoslanadi. Bu erda 12 11 dan katta, ular o sish tartibida emas va 12 o zining to g ri joyida ʻ ʻ ʻ ʻ emas. Shunday qilib, 11 va 12 ning o rnini almashtiring. ʻ Shunday qilib, hozircha 11 tartiblangan pastki qatorda saqlanadi. Ikkinchi o tish ʻ Endi keyingi ikkita elementga o ting va ularni solishtiring ʻ Bu erda 13 12 dan katta, shuning uchun ikkala element ham o sish tartibida turibdi, ʻ almashtirish sodir bo lmaydi. 12, shuningdek, 11 bilan birga tartiblangan pastki ʻ qatorda saqlanadi Uchinchi o tish ʻ Endi tartiblangan kichik massivda ikkita element mavjud, ular 11 va 12 Keyingi ikkita elementga o tish: 13 va 5 ʻ 5 va 13 ikkalasi ham o z joyida emas, shuning uchun ularni almashtiring ʻ Almashtirilgandan so ng, 12 va 5 elementlar tartiblanmadi, shuning uchun yana ʻ almashtiriladi Bu erda yana 11 va 5 tartiblanmadi, shuning uchun yana almashtiring bu erda u o zining to g ri holatida ʻ ʻ ʻ To rtinchi o tish ʻ ʻ Endi tartiblangan kichik massivda mavjud bo lgan elementlar 5, 11 va 12 ʻ Keyingi ikkita elementga o tish: 13 va 6 ʻ Shubhasiz, ular tartiblanmagan, shuning uchun ikkalasini almashtirishni amalga oshiring Endi 6 12 dan kichik, shuning uchun yana almashtiring Almashtirish 11 va 6 ni tartiblamaydi, shuning uchun yana almashtiring Nihoyat, massiv to liq tartiblangan. ʻ Quicksort algoritmi Tez saralash - Charlz Xoar tomonidan yaratilgan mashxur saralash algoritmidir . Ushbu algoritm n ta elementdan iborat massivni eng uzog i bilan O( ʻ n 2 ) vaqtda saralaydi. Biroq algoritm bajarilish tezligining matematik kutilmasi O( n log n ) ga teng va u boshqa shunday tezlikda bajariluvchi algoritmlardan tezroq ishlaydi. Ishlash printsipi 1.Massivda ixtiyoriy tayanch element tanlaymiz. 2.Keyin undan kichik yoki teng elementlarni uning chap tomoniga, katta elementlarni o ng tomoniga o tkazamiz. ʻ ʻ 3.1-2-chi qadamlarni tayanch elementning o ng va chap tomonlaridagi elementlar ʻ uchun qo llaymiz. ʻ Algorimning 2 qadami turlicha bo lib uning bir nechta realizatsiyalari mavjud. ʻ Ayni shu 2 qadamda elementlarni joylashtirish algoritmi tufayli algoritm saralash algoritmlari ichida eng tez ishlaydiganlaridan biridir. QuickSort pythondagi dasturi def tez_saralash(a): if len(a) <= 1: return a else: b= a[0] kichiklar = [i for i in a[1:] if i <= b] katta = [i for i in a[1:] if i> b] return tez_saralash(kichiklar) + [b] + tez_saralash(katta) # Misol qo llanishi: ʻ a = [5, 2, 9, 1, 7, 6, 3] z = tez_saralash(a) print(z) Merge sort Birlashtirib saralash algoritmi asosiy beshta saralash algoritmlari ( Bubble sort , Quick sort va boshqalar) dan biri bo lib, chiziqli saralash algoritmlaridan ʻ farqli ravishda „bo lib tashla va hukmronlik qil“ tipidagi algoritm hisoblanadi. Bu ʻ turdagi algoritmlar katta hajmdagi masalalarni nisbatan kichik bo lgan va oson ʻ yechiladigan qismlarga ajratgan holda bajaradi. Bunday algoritmlar masalalarni yechishda vaqtdan yutish imkonini beradi [1] . Merge sort algoritmi 1.Merge Sort funksiyasiga massiv va uning boshlang ich (eng chapdagi element) ʻ va oxirgi nuqtalari (eng o ngdagi element) beriladi. ʻ 2.Massivning o rtasi hisoblanadi: o rtasi = (chap + o ng)/2. Bu narsa uni teng ʻ ʻ ʻ ikkiga bo lish uchun kerak bo ladi. ʻ ʻ 3.Merge sortni rekursiv holda birinchi va ikkinchi qismlar uchun chaqiriladi. 4.2- va 3-qismlarda hosil bo lgan massivlar birlashtirib chiqiladi.ʻ Algoritm ishlash tezligi O(n*log(n)) bo lib tezligi O(n ʻ 2 ) bo lgan oddiy ʻ Bubble sort , Insertion sort , Selection sortlardan ancha tez ishlaydi. Taqqoslash asosida ishlaydigan algortmlarning eng tez ishlash holati O(n*log(n)) bo lishi ʻ isbotlangan [2] . 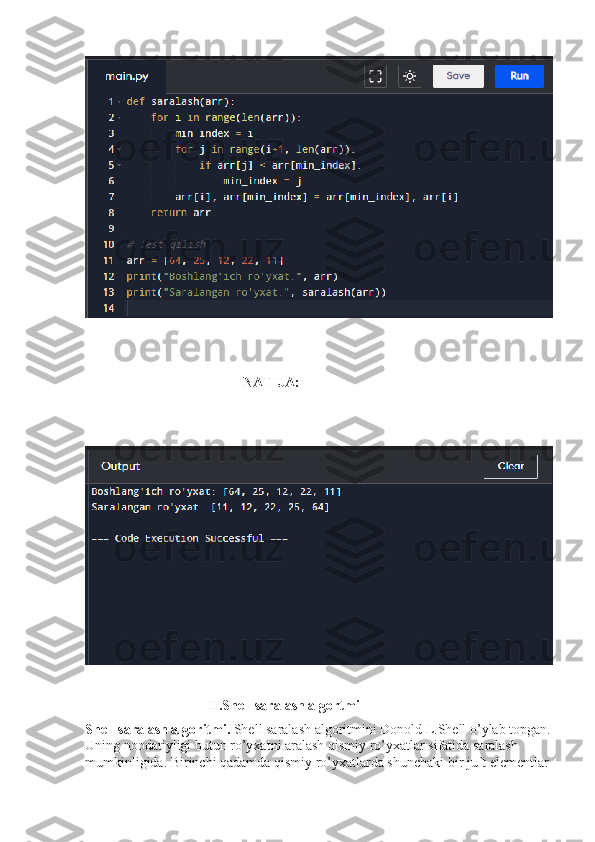Merge sort algorithm diagram Dastur: def saralash(arr): for i in range(len(arr)): min_index = i for j in range(i+1, len(arr)): if arr[j] < arr[min_index]: min_index = j arr[i], arr[min_index] = arr[min_index], arr[i] return arr # Test qilish arr = [64, 25, 12, 22, 11] print("Boshlang'ich ro'yxat:", arr) print("Saralangan ro'yxat:", saralash(arr)) NATIJA: II.Shell saralash algortmi Shell saralash algoritmi. Shell saralash algoritmini Donold L.Shell o’ylab topgan. Uning noodatiyligi butun ro’yxatni aralash qismiy ro’yxatlar sifatida saralash mumkinligida. Birinchi qadamda qismiy ro’yxatlarda shunchaki bir juft elementlar o’zaro o’rin almashadilar. Ikkinchi bosqichda har bir guruhdan to’rtta element o’rin almashadi.Ushbu jarayonni takrorlashda har bir qismiy ro’yxatlarda elementlar soni oshib, qismiy ro’yxatlar soni esa, mos holda kamayadi. 6.4-rasmda tarkibi 16 ta elementdan iborat ro’yxatni saralashda foydalanish mumkin bo’lgan qismiy ro’yxatlar tasvirlangan. 6.4-rasm. Shell saralash algoritmiga misol 6.4a-rasmda 8 ta qismiy ro’yxatlarni ajratib olish tasvirlangan bo’lib, har bir qismiy ro’yxatda 2 tadan element mavjud. 1–qismiy ro’yxat birinchi va to’qqizinchi elementlardan, 2–qismiy ro’yxat ikkinchi va o’ninchi elementlardan va h.k. tashkil topgan. 6.4b-rasmda har biri 4 ta elementdan iborat topgan to’rtta qismiy ro’yxat tashkil etilganligini ko’rishimiz mumkin. Bu yerda 1–qismiy ro’yxat birinchi, beshinchi, to’qqizinchi va o’n uchinchi elementlardan tashkil topgan. 2–qismiy ro’yxat esa ikkinchi, oltinchi, o’ninchi va o’n to’rtinchi elementlardan tashkil topgan. 6.4c-rasmda ikkita qismiy ro’yxat keltirilgan bo’lib, ular mos ravishda juft va toq o’rinlarda joylashgan elementlardan tashkil topgan. 6.4d-rasmda yana boshlang’ich holatdagidek bitta ro’yxatga kelamiz. Qismiy ro’yxatlarni saralash oldingi bo’limda o’rganilgan qo’yishlar orqali saralash algoritmini bir marta qo’llash yo’li bilan bajariladi. Natijada quyidagi algoritmga ega bo’lamiz: ShellSort(list,N) list -saralanadigan ro’yxat nomi N -ro’yxatdagi elementlar soni passes=[log_2N] while (passes>=1) do increment=2^passes-1 for start=1 to increment do InsertionSort(list,N,start,increment) end for passes=passes-1 end while increment o’zgaruvchisi qismiy ro’yxat elementlari o’rtasidagi qadam kattaligidan tashkil topadi (6.4-rasmdagi misolda qadam 8, 4, 2 va 1 qiymatlaridan tashkil topgan). Algoritmning birinchi qadamini, ro’yxat uzunligidan kichik bo’lgan 2 ning eng katta darajasidan bir birlikka kam bo’lgan qiymat bilan boshlaymiz. Bundan kelib chiqadiki, 1000 ta elementdan tashkil topgan ro’yxat uchun qadamning dastlabki qiymati 511 bo’ladi. Bundan tashqari qadam qiymati qismiy ro’yxatlar soniga teng bo’ladi. Birinchi qismiy ro’yxatning elementlari 1 va 1+increment o’rinlarda joylashgan bo’ladi, oxirgi qismiy ro’yxatning dastlabki elementi increment o’rinda turgan element bo’ladi. While siklining oxirgi qadamida passes o’zgaruvchisining qiymati 1 ga teng bo’ladi, shuning uchun IncrementSort funktsiyasining so’ngi chaqirilishida increment o’zgaruvchisining qiymati birga teng bo’ladi. Bu algoritm tahlili IncrementSort algoritmining ichki tahliliga asoslanadi. ShellSort algoritmini tahlil qilishdan oldin N ta elementdan tashkil topgan ro’yxatni qo’yishlar orqali saralashda eng yomon holat uchun ( N²–N )/2 amal bajarilishi, o’rtacha holatda esa bu algoritm N² /4 amal bajarilishini esga olishimiz zarur bo’ladi. Algoritm tahlili. Tahlilni IncrementSort funktsiyasiga murojaatlarni va har bir murojaatdagi ro’yxat elementlari sonini hisoblashdan boshlaymiz. Ro’yxat uzunligi 15 ga teng bo’lgan xususiy holatni qaraymiz. 1-qadamda increment o’zgaruvchisining qiymati 7 ga teng bo’ladi, shuning uchun uzunligi 2 ga teng bo’lgan ro’yxatlar uchun 7 marta IncrementSort funktsiyasiga murojaat bajariladi. 2-qadamda increment o’zgaruvchisining qiymati 3 ga teng bo’ladi, shuning uchun uzunligi 5 ga teng bo’lgan ro’yxatlar uchun 3 marta murojaat bajariladi. Oldingi natijalardan bilamizki, ikki elementli ro’yxatda algoritm eng yomon holda bitta taqqoslash bajaradi. Demak, 5 ta elementli ro’yxatda IncrementSort eng yomon holatda taqqoslashlar soni 10 ga teng bo’ladi. 15 ta elementli ro’yxatda esa eng yomon holatda taqqoslashlar soni 105 ga teng bo’ladi. Bu sonlarni qo’shib jami 142 ta (7*1+3*10+1*105) taqqoslashlarni hosil qilamiz. Qo’yishlar orqali saralashda eng yomon holat bo’lganida har bir yangi element ro’yxatning boshiga joylashtiriladi. Saralash algoritmlarini tahlil qilishda ro’yxatdagi inversiya lar sonini hisobga olamiz. Inversiya – ro’yxatning noto’g’ri tartibda keladigan bir juft elementlari. Masalan, [3,2,4,1] ro’yxatda 4 ta inversiya mavjud, bular (3,2), (3,1), (2,1) va (4,1). Bu yerda ko’rinib turibdiki, barcha inversiyalarda elementlar teskari tartibda joylashgan, shuning uchun taqqoslashlar soni eng ko’p bo’lib, ( N²–N )/2 ga teng bo’ladi. Tez saralash algoritmi . Bu saralash algoritmi saralashning yana bir rekuursiv algoritmi hisoblanadi. Tez saralash usulida ham berilgan ro’yxat tanlab olingan qiymat yordamida ikkiga ajratib olinadi. Bu algoritmning g’oyasi: to’g’ridan-to’g’ri almashtirish usulidagi saralash algoritmiga mos keladi, ya’ni tanlab olingan elementga nisbatan kichik yoki teng, katta yoki teng elementlar ikki tomonga ajratib olinadi (6.5-rasm). 6.5-rasm. Tezkor saralash algoritmi uchun misol 6.5-rasmda x=6 qiymatdan chap tomonda kichik, o’ng tomonda esa katta bo’lgan elementlar joylashishi uchun almashtirishga misol keltirilgan. Tezkor saralash da o’q element deb ataluvchi qiymat tanlab olinadi (6.5- rasmda bu qiymat 6 ga teng), so’ngra ro’yxat ushbu qiymatga nisbatan qayta tartiblanadi. O’q elementdan kichik qiymatlarning barchasi undan oldinga (chap tomonga), katta barcha elementlar undan keyinga (o’ng tomonga) joylashtiriladi. Ro’yxatning har bir qismi alohida tartiblanmaydi. Agar i o’q elementning oxirgi holati bo’lsa, u holda birinchi elementdan i– 1 gacha bo’lgan barcha elementlar o’q elementdan kichik, i + 1 dan N gacha bo’lgan elementlar o’q elementdan katta ekanligi ma’lum bo’ladi. Tez saralash algoritmi ro’yxatning har bir qismi uchun alohida rekursiv ravishda qo’llanilib, ro’yxat saralanadi. Tez saralash algoritmining asosiy vazifasi o’q elementni tanlab olish va elementlarni o’q elementga nisbatan o’rin almashtirishdan iborat. Tezkor saralash algoritmi quyidagicha tavsiflanadi: QuickSort (list, first, last) list – tartiblanadigan elementlar ro’yxati first –ro’yxatning tartiblanadigan qismining birinchi elementi last – ro’yxatning tartiblanadigan qismining oxirgi elementi if first < last then pivot=PivotList(list, first, last) QuickSort(list, first, pivot-1) QuickSort(list, first, pivot-1) QuickSort(list, pivot+1, last) end if Bu algoritm tarkibidagi PivotList funktsiyasining ikki xil varianti mavjud bo’lib, birinchi varianti tushunish va dasturlash oson bo’lib, ushbu bo’limda tavsiflanadi. Ikkinchi varianti tushunish qiyinroq bo’lgan, ammo tez ishlaydi. Bu variant mashqlarda tavsiflab o’tiladi. PivotList funktsiyasi o’q element sifatida ro’yxatning birinchi elementini oladi va pivot ko’rsatkichini ro’yxat boshiga o’rnatadi. So’ngra o’q elementni ro’yxatning boshqa elementlari bilan ketma-ket taqqoslab, undan kichik elementlar topilsa, PivotPoint ning qiymatini bir birlikka oshiradi va topilgan element o’rnini almashtiradi. Ro’yxatning birinchi qismi o’q element bilan taqqoslangach, u to’rtta qismga ajralib qoladi. Birinchi qism birinchi o’q elementdan tashkil topadi. Ikkinchi qism first+ 1 holatdan boshlanib, PivotPoint holat bilan tugaydi va o’q elementdan kichik bo’lgan barcha elementlardan tashkil topadi. Uchinchi qism PivotPoint +1 holatdan boshlanib, sikl ko’rsatkichi index bilan tugaydi. Ro’yxatning qolgan qism hali qarab chiqilmagan elementlardan iborat bo’ladi. Ro’yxatni bunday qismlarga bo’lish 6.6-rasmda tasvirlangan. 6.6-rasm. PivotList algoritmidagi ko’rsatkichlar qiymati PivotList algoritmi quyidagicha tavsiflanadi: PivotList (list, first, last) list – qayta ishlanadigan ro’yxat first – birinchi element nomeri last – oxirgi element nomeri PivotValue =list[first] PivotPoint =first for index=first+1 to last do if list[index] PivotValue then PivotPoint=PivotPoint+1 Swap (list[PivotPoint], list[index]) end if end for //o’q elementni kerakli o’ringa o’tkazish Swap (list[first], list[PivotPoint]) return PivotPoint Tez saralash algoritmining tahlili. Eng yomon holat. Elementlar soni N ta bo’lgan ro’yxatda bo’lganda PivotList protsedurasini chaqirish natijasida N- 1 ta taqqoslash bajariladi, chunki PivotValue ro’yxatning barcha elementlari bilan taqqoslanadi. Yuqorida ta’kidlanganidek, tez saralash “ bo’lib tashla va hukmronlik qil ” tamoyili asosida ishlaydi. Shuning uchun eng yaxshi holatda PivotList bir xil uzunlikdagi ikkita ro’yxat hosil qiladi deb fafraz qilish mumkin. Eng yomon holatda esa ro’yxatlar uzunliklari teng bo’lmasligi kerak. Qismiy ro’yxatlar uzunliklarining eng katta farqi, bu ajratib olingan o’q element ro’yxatning qolgan barcha elementlaridan eng kichik yoki eng katta bo’lgan holatda hosil bo’ladi. Bunday holda qismiy ro’yxatlardan birida birorta ham element bo’lmaydi, ikkinchisida esa N- 1 ta element bo’ladi. Agar har bir rekursiv chaqirish natijasida bunday qismiy ro’yxatlar hosil qilinsa, har bir chaqiruvda ro’yxatdan bitta elementni (PivotValue) o’chirish kerak bo’ladi. Bu esa taqqoslashlar sonini quyidagi formula yordamida aniqlash mumkinligini bildiradi: Agar algoritmning har bir o’tishida birinchi element tanlansa, u holda bu element eng kichik (eng katta) bo’lishi kerak. Oldindan tartiblangan ro’yxatda tez saralash algoritmini qo’llash eng yomon holatga misol bo’ladi. Algoritmning o’rtacha holat uchun tahlili. Eslatma: Shell saralash algoritmida har bir taqqoslash natijasida bitta inversiya o’chiriladi. “Pufakcha” va qo’yishlar orqali saralash algoritmlarining o’rtacha holatda tahlilida ham bitta taqqolash natijasida bitta inversiya o’chirilishini ko’rib o’tdik. Tez saralashda inversiyalar qanday o’chiriladi? Bu savolga javobni N ta elementdan iborat ro’yxat uchun PivotList algoritmini qo’llash orqali olamiz. Buning uchun PivotValue ning qiymati ro’yxatning barcha elementlaridan katta deb faraz qilamiz. Bu faraz protsedura bajarilishi natijasida PivotValue ning qiymati N ga teng bo’lishini bildiradi. Shuning uchun PivotValue o’zgaruvchisi ro’yxatning birinchi elementini emas, balki oxirgi elementini ko’rsatadi. Ro’yxatning oxirgi elementi esa shu ro’yxatning eng kichik elementi bo’lishi mumkin. Shuning uchun bu elementlar o’rnini almashtirish ro’yxatning eng katta elementini birinchi o’rindan oxiriga, eng kichigini oxiridan boshiga o’tkazish orqali bajariladi. Agar eng katta element birinchi o’rinda, eng kichik element oxirgi o’rinda turgan bo’lsa, ularning har biri alohida ro’yxatning boshqa elementlari bilan N- 1 ta inversiyani hosil qiladi. Shunday qilib, ikkita chetki elementlarning o’rnini almashtirish 2 N –2 inversiyani yo’q qiladi. Shu sababli, tez saralash algoritmi o’rtacha holati eng yomon holatdan sezilarli darajada farq qiladi. Tez saralash algoritmida PivotList algoritmi asosiy vazifani bajaradi. Shuning uchun ham ushbu algoritmni o’rtacha holat uchun tahlil qilamiz. Eng yomon holat tahlilida PivotList algoritmi N ta elementdan iborat ro’yxatni ikkiga bo’lib, N-1 ta taqqoslash bajarilishini ta’kidlab o’tgan edik. bu ro’yxatlarni birlashtirish hech qanday ish talab qilmaydi. Nihoyat yana ta’kidlash muhimki, PivotList algoritmi P qiymat qaytarganda, ikkita P–1 va N–P uzunlikdagi ro’yxatlar uchun QuickSort protsedurasini rekursiv chaqirishga to’g’ri keladi. Natijada quyidagi rekurent munosabatga ega bo’lamiz, A>2, A(1)=A(0)=0 uchun: Agar yig’indiga diqqat bilan e’tibor berilsa, birinchi qo’shiluvchining argumenti 0 dan N-1 gacha, ikkinchi qo’shiluvchining argumenti esa aynan shu qiymatlar, lekin kamayish tartibida o’zgaradi. Bundan kelib chiqadiki, A(i) qo’shiluvchi yig’indida ikki marta qatnashgan va yuqoridagi formulani quyidagicha soddalashtirish mumkin, N>=2, A(1)=A(2)=0 uchun: Munosabatning bu ko’rinishi juda murakkab, chunki, А(N) faqat kichik argumentlar bilan emas, balki birdaniga barcha argumentlar orqali ifodalangan. Bu murakkablikdan qutulish uchun maxrajni yo’qotamiz va A(N), A(N-1) holatlar uchun quyidagilarga ega bo’lamiz: Natijada, ikkinchi tenglikdan birinchi tenglikni ayirib, quyidagicha soddalashtirishga ega bo’lamiz: Hosil qilingan tenglikning ikkala tomoniga ham A(N-1)*(N-1) ni qo’shib quyidagiga ega bo’lamiz: Bundan esa quyidagi rekurent munosabatni keltirib chiqarish mumkin: Bu munosabatning yechimini olish qiyin emas, ammo tenglikning o’ng tomonida barcha mumkin bo’lgan qo’shiluvchilarni hisoblashda ehtiyotkorlik talab etiladi. Ushbu munosabatdan kelib chiqqan holda ekanligini aniqlash mumkin. Shunday qilib, tez saralash algoritmining samaradorligini deb olish mumkin ekan. XULOSA Saralash algoritmlaridan biri bo ʼ lgan Shell saralash algoritmidan shuni xulosa qilib aytish mumkinki , Shell saralash algoritmi bir biridan uzoqda joylashgan elementlarni almashish imkonini beruvchi qo ʼ shish saralash algoritmiga asoslangan samarali saralsh usulidir . Shell tartiblash algoritmidagi optimallashtirishlar o ʼ sish ketma - ketligini tanlash , o ʼ tishlarni qisqartirish va yaxshi ishlash uchun samarali ketma - ketligini o ʼ z ichiga oladi . Ushbu optimallashtirishlarni amalga oshirish orqali Shell saralsh algoritmi tezroq saralash algoritmi vaqtlariga erishadi va turli ma ʼ lumotlar to ʼ plamlariga yaxshiroq moslashadi , bu uni ko ʼ p qirrali saralash usuliga aylantiradi . Shell sortining asosiy xususiyatlaridan biri shundaki u taqqoslanadigan elementlar orasidagi bo ʼ shliqni asta sekin qisqartiradi , bu esa oddiy kiritish algoritmilari bilan solishtirganda yaxshilangan ishlashga olib keladi . Samaradorligiga qaramay Shell sortining murakkablik tahlili tanlangan bo ʼ shliqlar ketma - ketligi tufayli qiyin bo ʼ lishi mumkin . Saralangan yoki deyarli tartiblangan ma ʼ lumotlarga qo ʼ llanilganda , Shell saralash uning tezligini sezilarli darajada oshirish va kerakli taqqoslashlar sonini kamaytirishi mumkin . Biroq yuqori darajada tasodifiylashtirilgan ma ʼ lumotlar to ʼ plamlarida Shell saralshning ishlashi qisman saralangan ma ʼ lumotlardagi kabi samarali bo ʼ lmasligi mumkin . Shell saralsh algoritmini amalga oshirishda keng tarqalgan xatolardan biri bo ʼ shliq o ʼ lchamlarini noto ʼ g ʼ ri hisoblashdir . Bo ʼ shliq qiymatlarini aniq aniqlash uchun matematik naqshini tushunish juda muhim . Bundan tashqari taqqoslash va almashtirish bosqichlarining bajarilishini e ʼ tiborsiz qoldirish saralash jarayonida xatolarga olib kelish mumkin . Ko ʼ pincha qilingan yana bir xato bu - oxirgi iteratsiyani noto ʼ g ʼ ri ishlatish . Barcha elementlarning to ʼ g ʼ ri tartiblanganligiga ishonch hosil qilsih kerak , shu jumladan oldingi bo ʼ shliqlarni hisoblashda o ʼ tkazib yuborishi mumkin bo ʼ lgan elementlar . Shell saralash algoritmi turli xil ma ʼ lumotlar to ʼ plamlari bo ʼ yicha o ʼ zining samaradorligi bilan mashhur bo ʼ lib , har xil turdagi ma ʼ lumotlarda ta ʼ sirchan ishlashni ko ʼ rsatadi . Xulosa qilib aytganda ,Shell saralsh algoritmi ma lumotlarni saralash uchunʼ kuchli vositadir. Algoritmning turli xil ma lumotlar turlariga moslashishi va unumdorlikni ʼ optimallashtirishdagi samaradorligini aniqlashning asosiy jihatlari.Umuman olganda ,Shell tartiblash algoritmini amalga oshirish turli ilovalarda saralash operatsiyalaring tezligi va samaradorligini sezilarli darajada oshirishi mumkin FOYDALANILGAN ADABIYOTLAR 1.Algoritm va Dasturlash asoslari . A.R.Azamatov . Toshkent-2013 2.Algortmlar . M.O’.Ashurov , SH.A.Sattorova,SH.U.Usmonqulov.Toshkent-2016 Internet manbalari 1. https://uz.wikipedia.org/wiki/Saralash_algoritmi 2. https://www.texnoman.uz/post/2-saralash-algoritmlari.html 3. https://javarush.com/uz/groups/posts/uz.1997.nazariy-va-amaliyotda- saralash-algoritmlari

Mavzu : Shell saralash al gortmi Reja : I.Kirish II.Asosiy qism 1.Shell saralash algortmi. 2. Algoritmning tahlili. 3. Tez saralash algoritmining tahlili. III Xulosa IV Foydalanilgan adabiyotlar

KIRISH Saralash tushunchasi Saralash - tartiblash (Sorting algorithms) deb, berilgan obyektlar ketma-ketligini malum mantiqiy tartibda qayta joylashtirish jarayoniga aytiladi. Saralash bir nechta ko'rsatkichlarga bog'liq bo'lishi mumkin. Misol uvhun maktab jurnalida o'quvchilar familiyasi alifbo tartibiga ko'ra saralangan bo'ladi. Masalan bizga sonlar qatori berilgan: 8,23,0,-50,100 bu qatorni kichigidan kattasiga qarab yoki kattasidan kichigiga qarab saralashishimiz mumkin. Bu saralashni amalga oshirish jarayoni Saralash algoritmi deyiladi Saralash algoritmlari ko'p va xilma-xil. Saralash algoritmlari ikki tipga bo'linadi. - O() vatda saralovchi algoritmlar. Yani kvadratik amallar talab qiladigan algoritmlar - O(n*log(N)) vaqtda saralovchi algoritmlar. Logarifmik amallar soni talab qiladigan algoritmlar Saralash algoritmi va turlari - Bubble sort (Pufakchali saralash) - Selection sort (Tanlab saralash) - Insertion sort (Joylashtirib saralash) - Quick sort (Tezkor saralash) - Merge sort (Qo'shib saralash) Bubble sort Bu eng sodda, ketma-ketlikdagi har bir sonni boshqa sonlar bilan solishtirishga asoslangan algoritm hisoblanadi. Unda yonma-yon turgan elementlardan chapdagisi o‘ngdagidan kattaligi aniqlansa, bu ikkala son o rni almashtiriladi. Bu ʻ jarayon almashtirish kerak bo lmay qolguncha davom etadi, ya ni barcha ʻ ʼ elementlar o‘sish tartibida bo‘lib qolguncha. Algoritmi va dasturi public class BubbleSort { public static void main(String[] args) { int[] massiv = { 4, 2, 9, 6, 23, 12, 34, 0, 1 };

int n = massiv.length; int k; for (int m = n; m &gt;= 0; m--) { for (int i = 0; i &lt; n - 1; i++) { k = i + 1; if (massiv[i] &gt; massiv[k]) { int temp; temp = massiv[i]; massiv[i] = massiv[k]; massiv[k] = temp; } } for (int i = 0; i &lt; massiv.length; i++) { System.out.print(massiv[i] + ", "); } System.out.println(„\n“); } } } Chiqariluvchi natijamiz esa: 2, 4, 6, 9, 12, 23, 0, 1, 34, // 1-qadam. 2, 4, 6, 9, 12, 0, 1, 23, 34, //2-qadam. 2, 4, 6, 9, 0, 1, 12, 23, 34,//3-qadam. 2, 4, 6, 0, 1, 9, 12, 23, 34,//4-qadam. 2, 4, 0, 1, 6, 9, 12, 23, 34,//5-qadam.

2, 0, 1, 4, 6, 9, 12, 23, 34,//6-qadam. 0, 1, 2, 4, 6, 9, 12, 23, 34, //7-qadam. 0, 1, 2, 4, 6, 9, 12, 23, 34, //8-qadam. 0, 1, 2, 4, 6, 9, 12, 23, 34,//9-qadam. 0, 1, 2, 4, 6, 9, 12, 23, 34, // saralangan holdagi massiv. Selection sort Tanlab saralash bu — oddiy tartiblash algoritmidir. Ushbu tartiblash algoritmi o z ʻ joyida taqqoslashga asoslangan algoritm bo lib, unda ro yxat ikki qismga ʻ ʻ bo linadi, tartiblangan qism chap tomonda va tartiblanmagan qism o ng tomonda. ʻ ʻ Dastlab, tartiblangan qism bo sh, tartiblanmagan qismi esa butun ro yxatdir. ʻ ʻ Eng kichik element tartiblanmagan massivdan tanlanadi va eng chap element bilan almashtiriladi va bu element tartiblangan massivning bir qismiga aylanadi. Bu jarayon tartiblanmagan massiv chegarasini bitta element bilan o ngga siljitishda ʻ davom etadi. Ushbu algoritm katta ma lumotlar to plamlari uchun mos emas, chunki uning ʼ ʻ o rtacha va eng yomon holatlari murakkabligi n (n), bu yerda n ʻ — elementlar soni. Ishlash printsipi. Misol tariqasida quyidagi massivni ko rib chiqamiz: arr[] = {64, 25, 12, 22, 11} ʻ Birinchi o tish: ʻ Saralangan massivdagi birinchi o rin uchun butun massiv 0 dan 4 gacha bo lgan ʻ ʻ indeksdan ketma-ket o tkaziladi. Hozirgi vaqtda 64 saqlanadigan birinchi ʻ pozitsiya, butun massivni aylanib o tgandan so ng, 11 eng past qiymat ekanligi ʻ ʻ ayon bo ladi. ʻ

Shunday qilib, 64 ni 11 bilan almashtiring. Bir iteratsiyadan so ng massivdagi eng ʻ kam qiymat bo lgan 11 , tartiblangan ro yxatning birinchi pozitsiyasida paydo ʻ ʻ bo ladi. ʻ Ikkinchi o tish: ʻ 25 mavjud bo lgan ikkinchi pozitsiya uchun massivning qolgan qismini yana ʻ ketma-ketlikda aylantiring. Ketishdan so ng biz 12 massivdagi ikkinchi eng past qiymat ekanligini va u ʻ massivda ikkinchi o rinda paydo bo lishi kerakligini aniqladik, shuning uchun bu ʻ ʻ qiymatlarni almashtiring. Uchinchi o tish: ʻ Endi, uchinchi o rin uchun, 25 mavjud bo lgan joyda yana massivning qolgan ʻ ʻ qismini aylanib o ting va massivdagi uchinchi eng kam qiymatni toping. ʻ Ketish paytida 22 uchinchi eng kam qiymat bo lib chiqdi va u massivda uchinchi ʻ o rinda paydo bo lishi kerak, shuning uchun 22 ni uchinchi o rindagi element bilan ʻ ʻ ʻ almashtiring. To rtinchi o tish: ʻ ʻ Xuddi shunday, to rtinchi pozitsiya uchun massivning qolgan qismini kesib o ting ʻ ʻ va massivdagi to rtinchi eng kichik elementni toping. ʻ 25 4-eng past qiymat bo lgani uchun u to rtinchi o rinni egallaydi. ʻ ʻ ʻ Beshinchi o tish: ʻ Nihoyat, massivda mavjud bo lgan eng katta qiymat avtomatik ravishda ʻ massivning oxirgi pozitsiyasiga joylashtiriladi Olingan massiv tartiblangan massivdir. Insertion sort (Joylab saralash) ham tartibsiz massiv elementlarini saralash uchun mo ljallangan. Uning ishlash algoritmi xuddi qo ldagi kartani saralashga o xshab ʻ ʻ ʻ

Похожие

MA’LUMOTLARNI SARALASH. SARALASHNING SHELL ALGORITIMI
Farak-Kolton va Bender algortmi
Saralash algoritmlari
Ma’lumotlarni saralash usullari
Timsort saralash algoritmi