Ikkinchi tartibli egri chiziqlar • Ikkinchi tartibli egri chiziqning umumiy tenglamasi • Ellips • Giperbola • Parabola

Ikkinchi tartibli egri chiziqning umumiy tenglamasi Ikkinchi tartibli egri chiziqlarga quyidagilar kiradi: ellips , uning alohida holati aylana , giperbola va parabola . x va y uchun ikkinchi darajali tenglama bilan berilgan :0 2 2 2 2 2       F Ey Dx Cy Bxy Ax Ikkinchi tartibli egri chiziqning umumiy tenglamasi Ayrim maxsus holatlarda bu tenglama ikkita chiziq, nuqta yoki xayoliy joyni ham belgilashi mumkin.

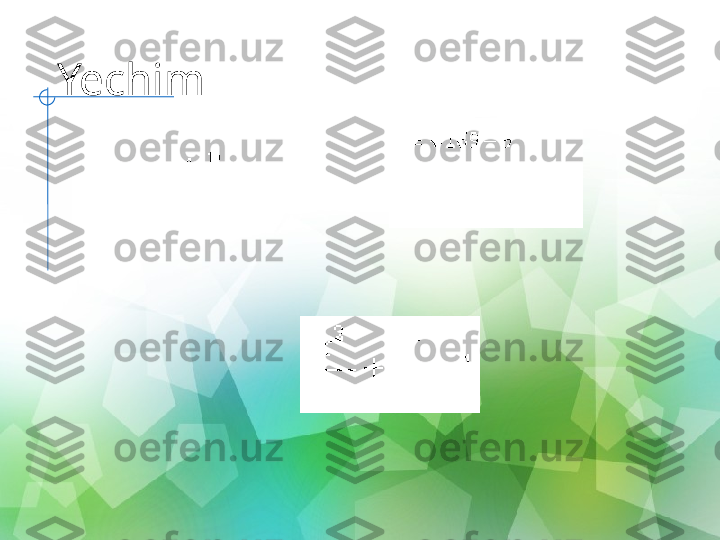
Ellips Ellips nuqtalarning joylashuvi, ularning har biridan bir tekislikning ikkita nuqtasiga bo'lgan masofalar yig'indisi F 1 va F 2 , fokuslar deb ataladi , 2a ga teng doimiy qiymat va F 1 F segmentining o'rtasi. 2 - ellipsning y 0 XF1 _ F 2 _-c cM(x; y) r1 _ r2 _a r r 2 2 1  Biz koordinatalar tizimini o'rnatamiz va segmentning o'rtasida koordinatalarning kelib chiqishini tanlaymiz [ F 1 F 2 ] ) 0 ; ( ); 0 ; ( 2 1 c F c F    2 2 1 1 y c x M F r       2 2 2 2 y c x M F r    

Ellips 1 2 2 2 2   b y a x Ellipsning kanonik tenglamasi

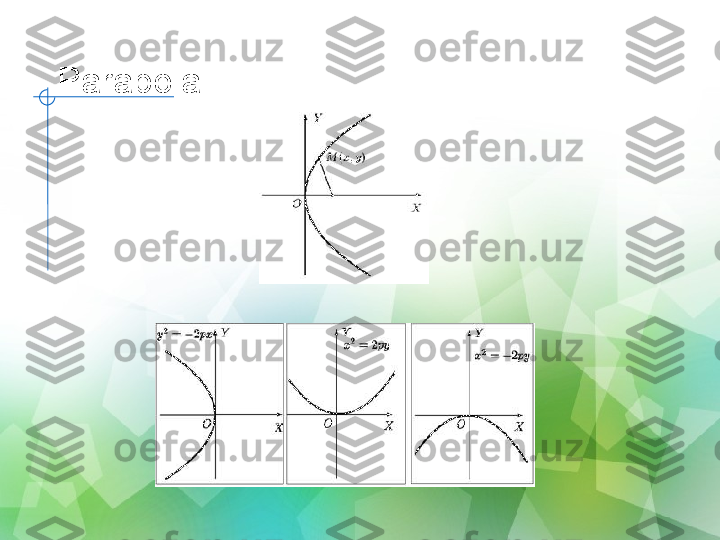
Ellips bu yerda a > 0, b > 0, a > b > 0 ellipsning katta va kichik yarim o‘qlari bo‘lsa, u holda ellips fokuslari x o‘qida simmetrik joylashgan va koordinatalariga (−c, 0) va (c, 0), qayerda e = c/a qiymati ellipsning ekssentrisiteti deb ataladi