Uch perpendikulyar haqida teorema

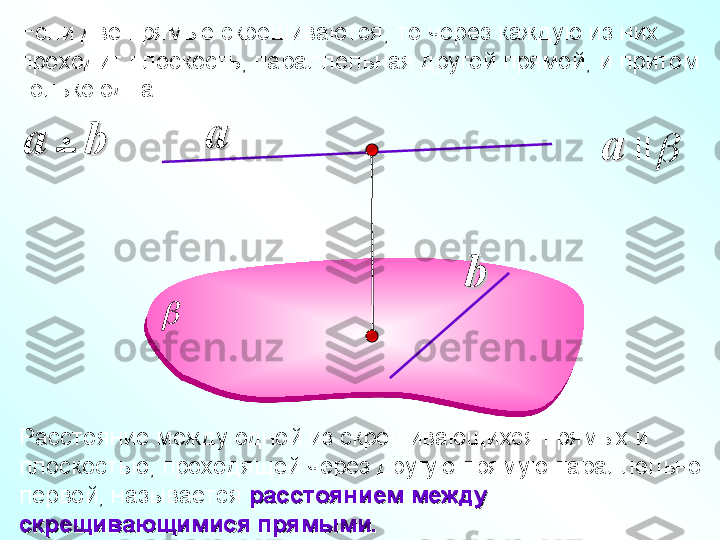

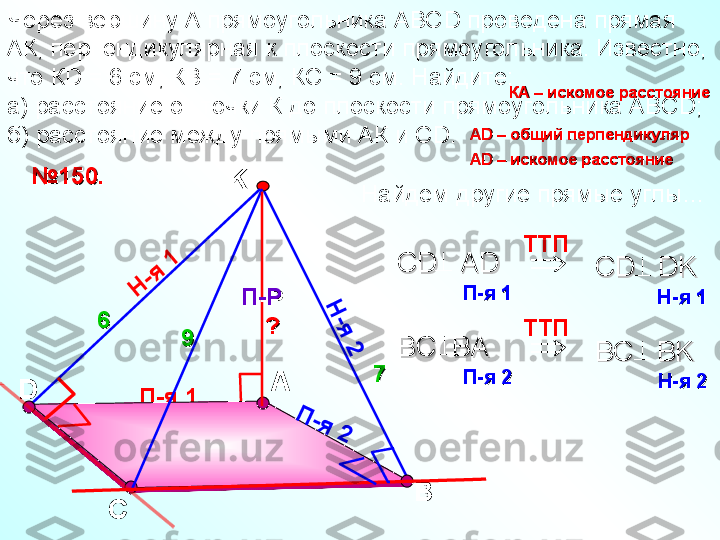
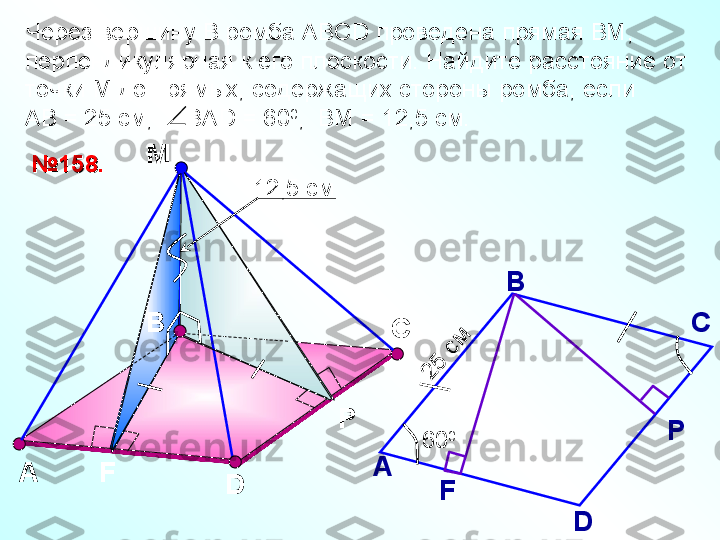


aa IIЕсли две прямые скрещиваются, то через каждую из них проходит плоскость, параллельная другой прямой, и притом только одна. aa Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между расстоянием между скрещивающимися прямыми.скрещивающимися прямыми. bbaa bb
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между расстоянием между скрещивающимися прямыми.скрещивающимися прямыми. Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к этим прямым, называется их общим перпендикуляром. На рисунке АВ – общий перпендикуляробщий перпендикуляр . ААВВ
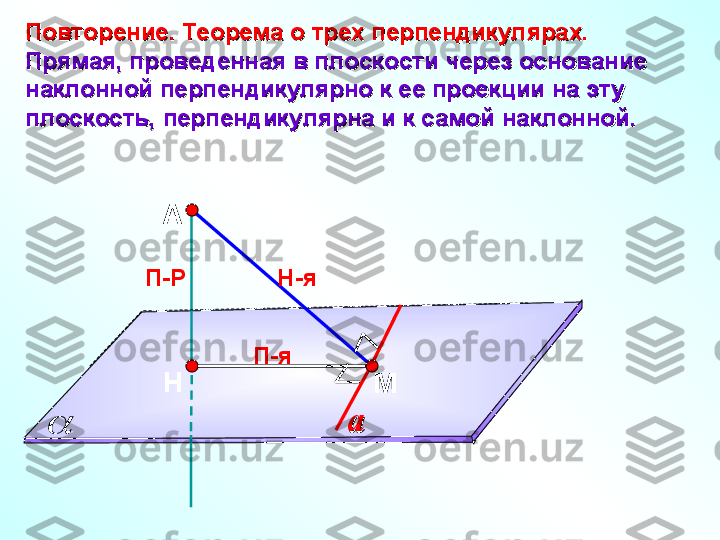
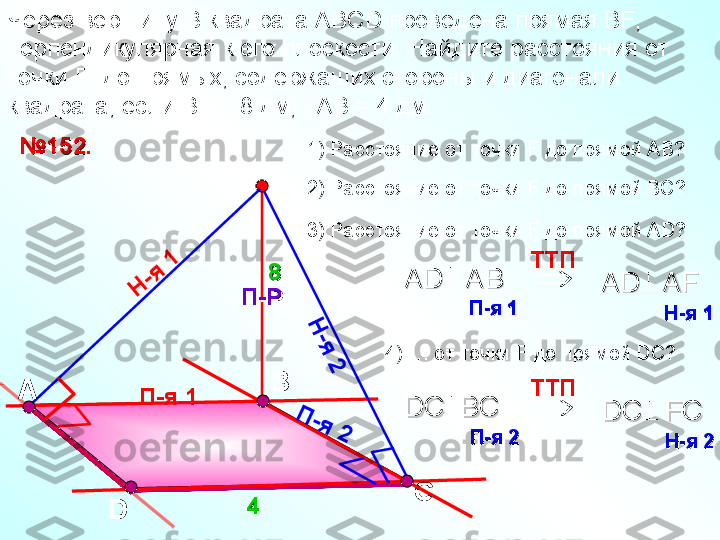
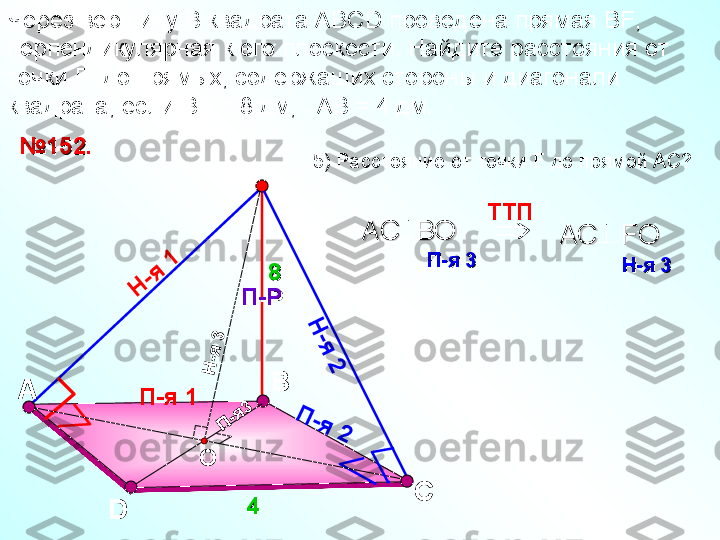
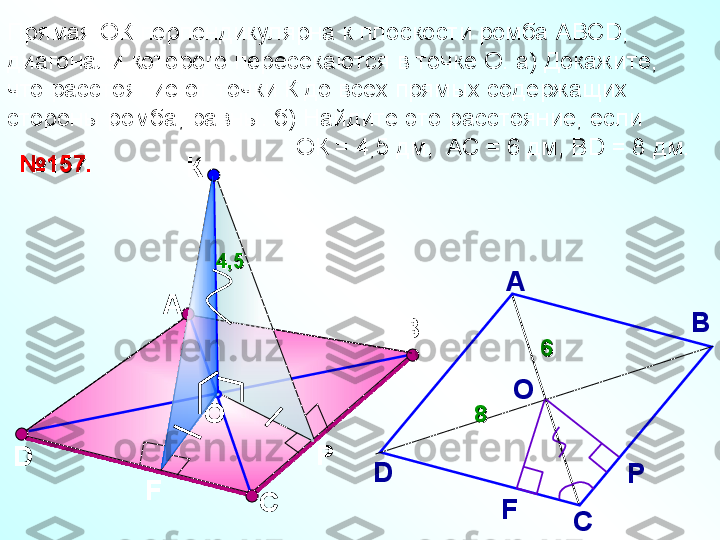
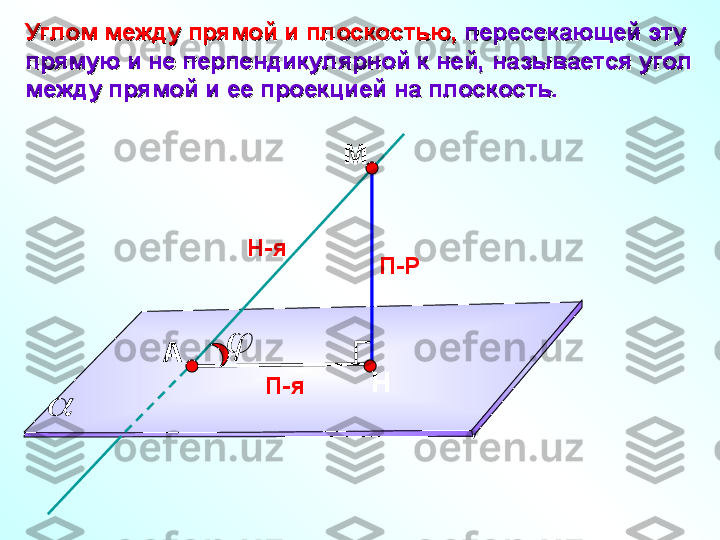
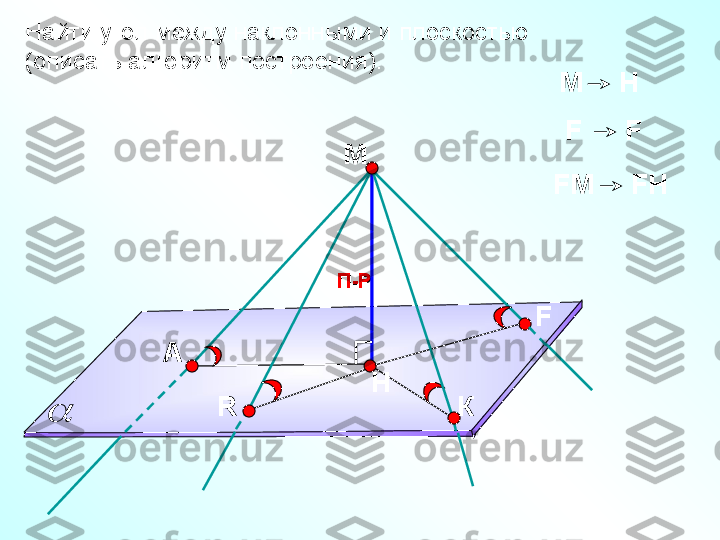
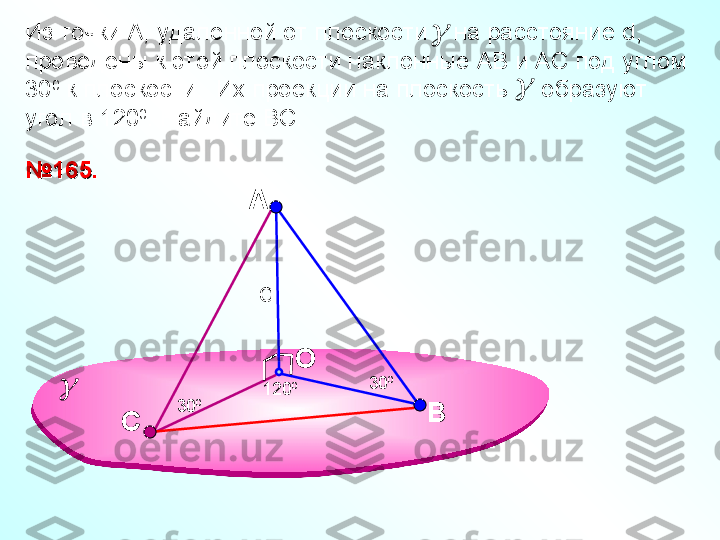
А НП-Р МПовторение. Теорема о трех перпендикулярах.Повторение. Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.плоскость, перпендикулярна и к самой наклонной. Н-я П-я aa
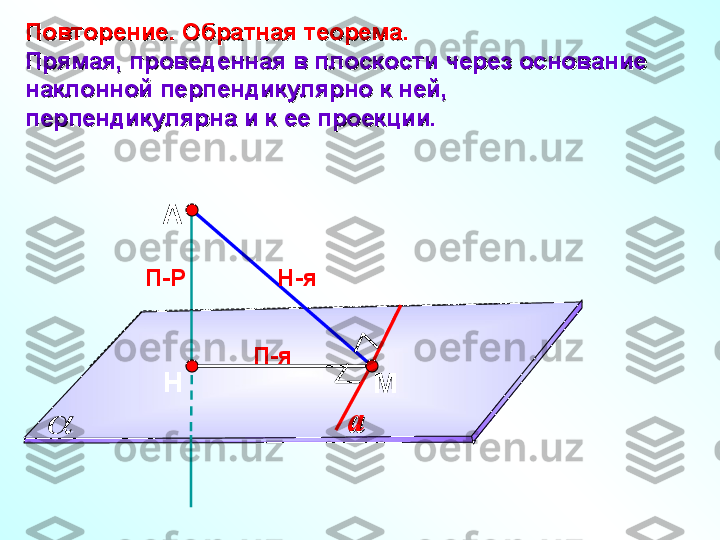
А НП-Р МПовторение. Обратная теорема.Повторение. Обратная теорема. Прямая, проведенная в плоскости через основание Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.перпендикулярна и к ее проекции. Н-я П-я aa
