ALGORITMLAR VA MA’LUMOTLAR








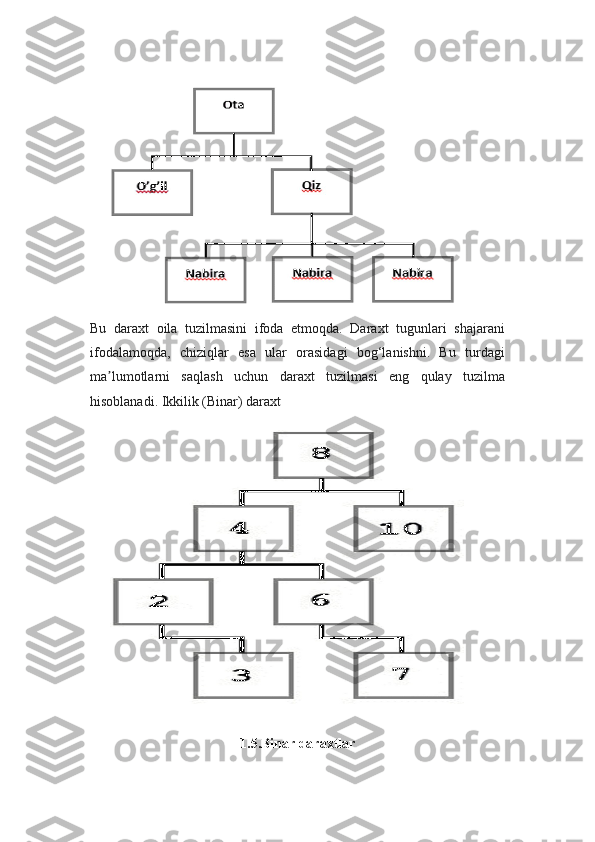


![To'liq ikkilik daraxt balandligi 3 10 Tugunli to'liq ikkilik daraxt va
balandligi.
Massivning atributlari
Ikki atributga ega bo'lgan ikkilik daraxtni taqdim etuvchi A
massivi:
uzunlik[A]: massivdagi elementlar soni.
massiv-o'lchami[A]: massiv bilan saqlanadigan elementlar soni
massiv A.
uzunlik[A] ≥ massiv o'lchami[A]
Asosiy protseduralar1/2
Agar n ta tugunli to liq binar daraxt ko rsatilgan bo lsaʻ ʻ ʻ
ketma-ket, keyin i, 1 ≤ i ≤ n indeksli har qanday tugun uchun
mavjud
A[1] - daraxtning ildizi
PARENT(i) ⌊ i/2 ⌋ , agar i ≠ 1 bo lsa
ʻ
chap uch LEFT(i) 2i da
o'ng uch O'NG(i) 2i 1 da](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_13.png)
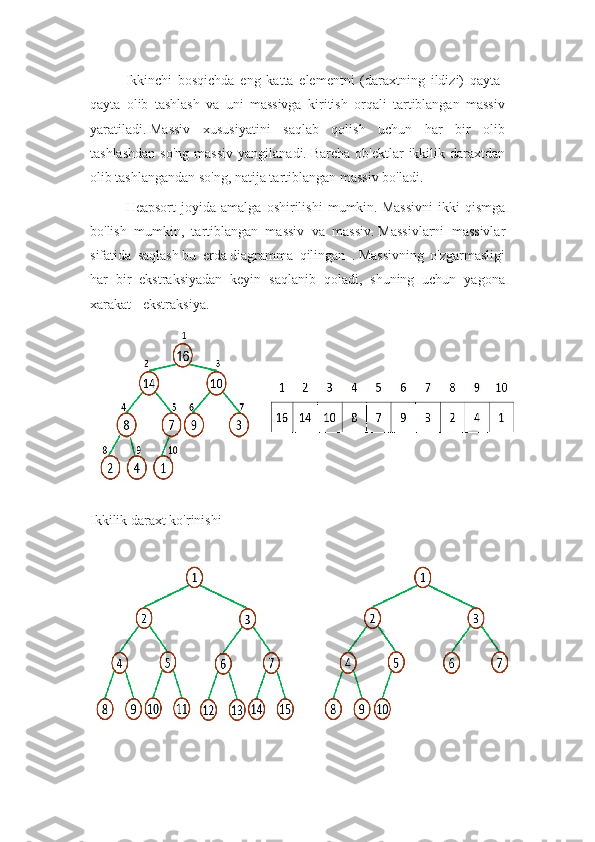
![Asosiy protseduralar2/2
LEFT protsedurasi bitta ko'rsatmada 2i ni oddiygina
hisoblashi mumkin i ning ikkilik ko'rinishini o'zgartirish bir
bir pozitsiyasini qoldirdi.
Xuddi shunday, RIGHT protsedurasi 2i 1 ni tezda hisoblashi
mumkin
i ning ikkilik tasvirini siljitish bir bir pozitsiyani qoldirdi va
past tartibli bir sifatida 1 ni qo'shish.
-PARENT protsedurasi i ni o'ngga siljitish orqali ⌊ i/2 ⌋ ni
hisoblashi mumkin bir holati
Massiv xususiyatlari
Ikki xil ikkilik massivlar mavjud: max-heaps va min-heaps.
Max-heapda max-heap xossasi har bir i tugun uchun
ildizdan tashqari,
A[PARENT(i) ] ≥ A[i] .
max-massividagi eng katta element ildizda saqlanadi
tugunga ildiz o’tgan pastki daraxt bundan katta bo'lmagan
qiymatlarni o'z ichiga oladi tugunning o'zida joylashgan
min-heapda min-heap xossasi har bir tugun uchun i
ildizdan tashqari,
A[PARENT(I)] ≤ A[I].
min-uyidagi eng kichik element ildizda joylashgan](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_14.png)
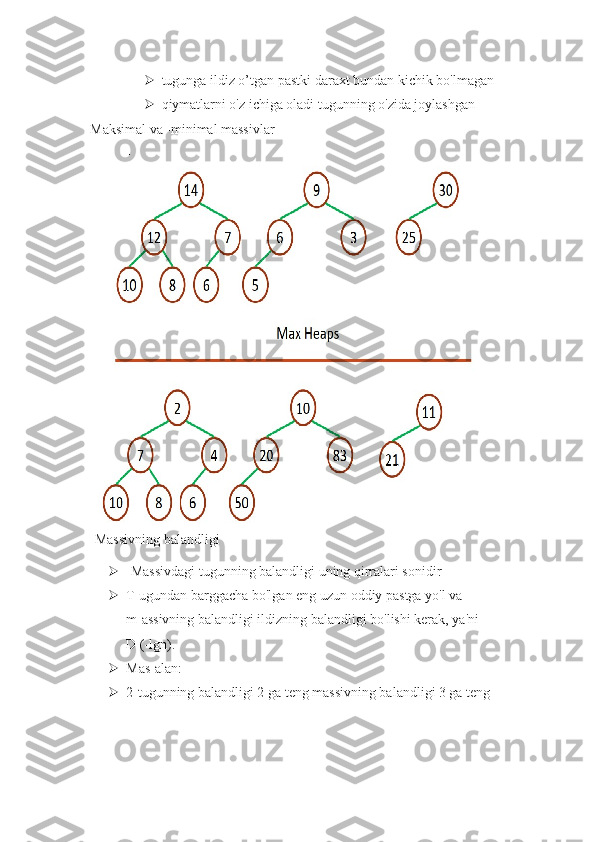
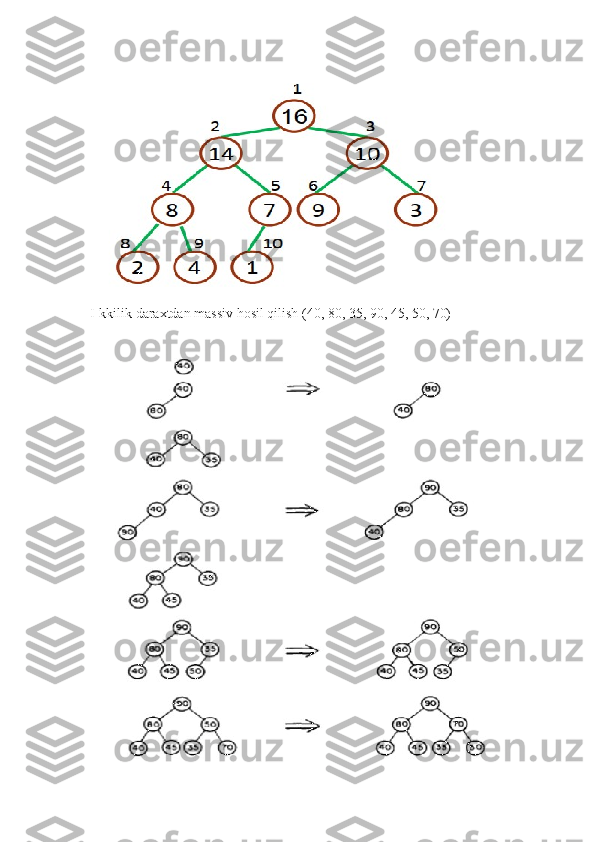
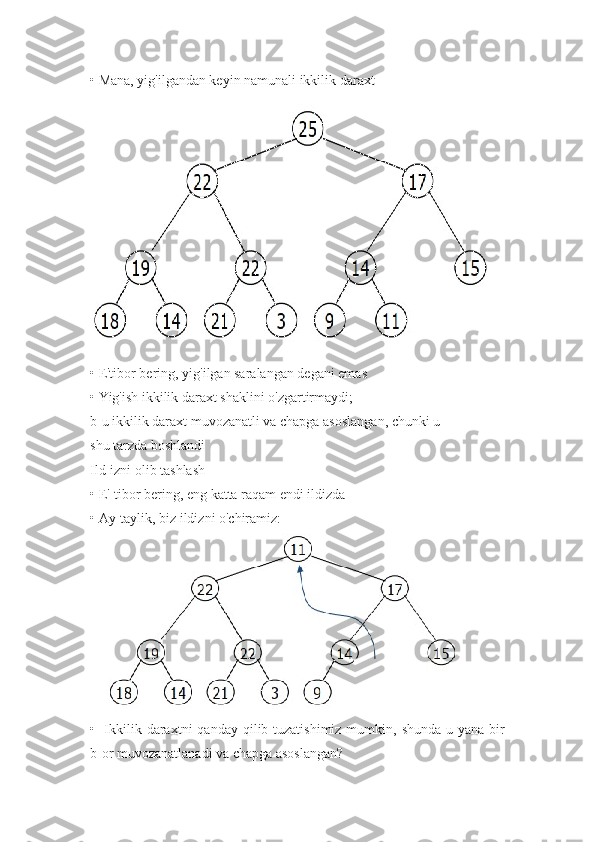
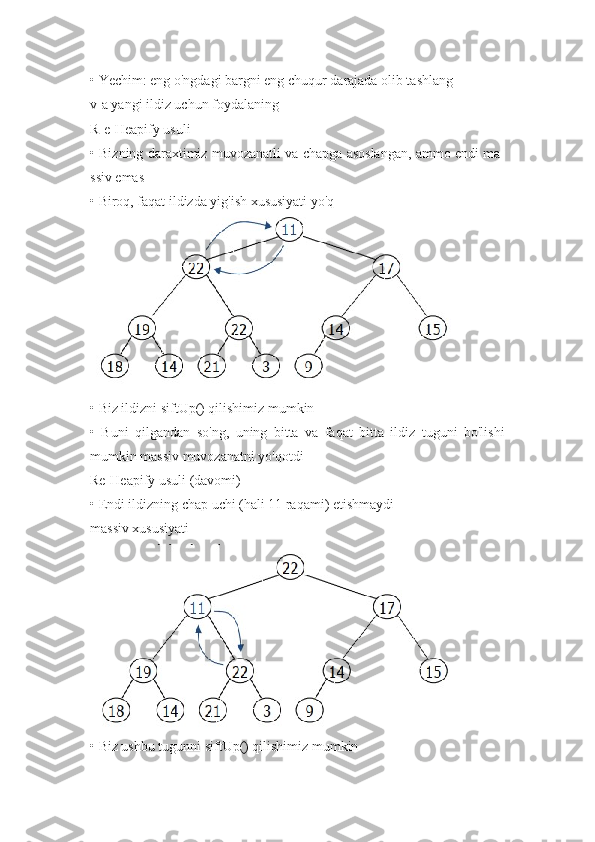


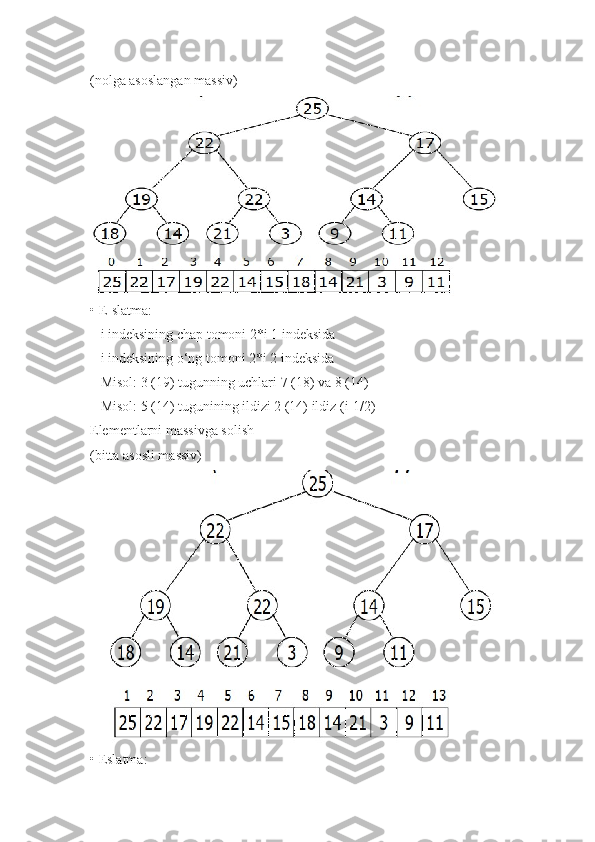


![ Natija: i indeksida ildiz o’tgan pastki daraxt maksimal uchga
aylanadi
Faraz qilaylik: LEFT(i) va RIGHT(i) ga ildiz o’tgan ikkilik
daraxtlar
max-massivlar, lekin A[i] uning uchlaridan kichikroq bo'lishi
mumkin
Usul: A[i] dagi qiymat max-ikkilik daraxtda "pastga tushib ketsin"
MAX-HEAPIFY protsedurasi2/2
MAX HEAPIFY(A, ‐ i )
1. l ←LEFT( i )
2. r ← RIGHT( i )
3. if l ≤ heap size
‐ [A] and A[ l ] > A[ i ]
4. then largest ← l
5. else largest ← i
6. if r ≤ heap size
‐ [A] and a[ r ] > A[ largest ]
7. then largest ← r
8. if largest ≠ i
9. then exchange A[ i ] A[ largest ]
10. MAX HEAPIFY (A,
‐ largest )
MAX-HEAPIFY protsedurasiga misol](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_24.png)
![Vaqtning murakkabligi
O'zaro munosabatlarni o'rnatish uchun D(1) vaqt kerak bo'ladi
A[i], A[LEFT(i)] va A[RIGHT(i)] elementlari.
Shuningdek, biz MAX-HEAPIFY ni biriga ildiz o’tgan pastki
daraxtda ishga tushirishimiz kerak i tugunining uchlari.
Uchlar pastki daraxtlarining har biri ko'pi bilan 2n/3 o'lchamga ega
Eng yomon holat daraxtning oxirgi qatori to'liq yarmiga to'lganida
sodir bo'ladi
MAX-HEAPIFY ish vaqti
T ( n ) = T (2 n /3) + Θ (1) = O (lg n)
Uni bosh teoremaning 2-holatiga ko'ra yeching
Shu bilan bir qatorda biz MAX-ning ishlash vaqtini tavsiflashimiz
mumkin.
O(h) kabi h balandlikdagi tugunga HEAPIFY.](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_25.png)
![ Massivni aylantirish uchun MAX-HEAPIFY protsedurasidan
foydalanishimiz mumkin A=[1..n] ni pastdan yuqoriga qarab maks.
A[( ⌊ n/2 ⌋ 1)…n ] pastki massivdagi elementlarning barchasi
quyidagi barglardir. daraxt, shuning uchun har biri 1 elementli
massivdir.
BUILD-MAX-HEAP protsedurasi qolgan qismidan o'tadi
daraxt tugunlari va har birida MAX-HEAPIFY ishlaydi
BUILD MAX HEAP(A)‐ ‐
1. heap size
‐ [A] ← length [A]
2. for i ← ⌊ length[A] /2 ⌋ downto 1
3. do MAX HEAPIFY(A,
‐ i )
Misol](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_26.png)
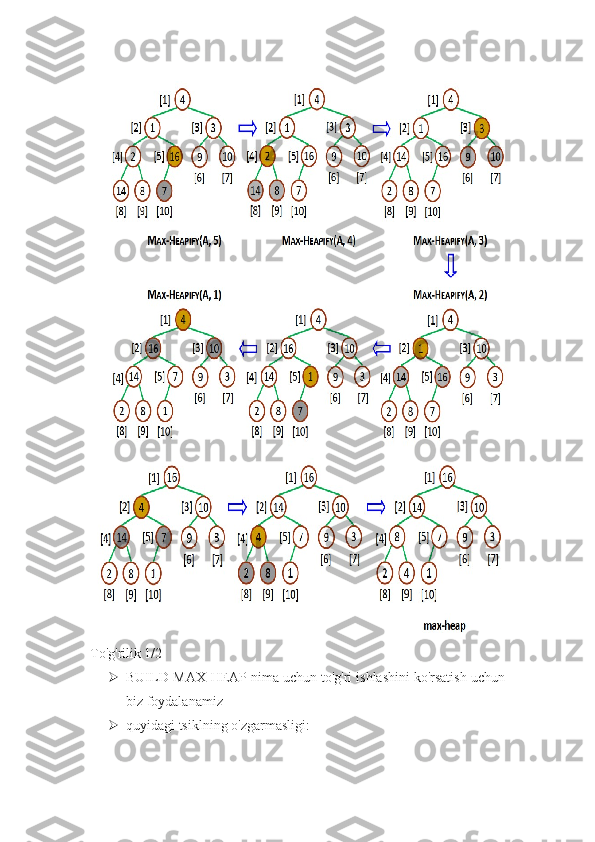
![ 2-3-qatorlardan iborat for tsiklining har bir iteratsiyasi boshida, har
biri i 1, i 2, …, n tugun max-daraxtning ildizidir
BUILD MAX HEAP(A)‐ ‐
1. heap size
‐ [A] ← length [A]
2. for i ← ⌊ length[A] /2 ⌋ downto 1
3. do MAX
Biz buni ko'rsatishimiz kerak
bu invariant birinchi sikl iteratsiyasidan oldin rost
siklning har bir iteratsiyasi o'zgarmaslikni saqlaydi
o'zgarmas to'g'rilikni ko'rsatish uchun foydali xususiyatni beradi
sikl tugagach
To'g'rilik 2/2
Initializatsiya: siklning birinchi iteratsiyasidan oldin, i = ⌊ n/2 ⌋ .
⌊ n/2 ⌋ 1, …n barg va shuning uchun a ning ildizi hisoblanadi
arzimas maksimal massiv.
Ta'minot: Loop o'zgarmasligiga ko'ra, i tugunining uchlari
maksimal massivlarning ikkala ildizi. Bu aniq
MAX-HEAPIFY (A, i) chaqiruvi uchun zarur shart
i tugunini max-heap ildiziga aylantirish. Bundan tashqari,
MAX-HEAPIFY chaqiruvi ushbu xususiyatni saqlaydi
tugunlar i 1, i 2, . . . , n - max-massivlarning barcha ildizlari.
Tugatish: Tugatishda i=0. Loop invariant bo'yicha, har bir tugun
1, 2, …, n max-daraxtning ildizidir.
Xususan, 1-tugun.
Vaqt murakkabligi1/2
1-tahlil:
MAX-HEAPIFY ga har bir murojaat O(lgn) turadi va
bunday O(n) mavjud](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_28.png)

![Massivni tanlash algoritmi
Massivning maksimal elementi ildizda saqlanganligi sababli,
A[1] biz uni A[n] bilan almashtira olamiz.
Agar biz hozir A[n] ni “tashlab qo'ysak”, A[1...(n−1)] osonlik bilan
bo'lishi mumkinligini ko'ramiz. maksimal massivga aylantiriladi.
A[1] ildizining uchlari max-massivlar bo'lib qoladi, lekin yangi
root A[1] elementi max-heap xususiyatini buzishi mumkin,
shuning uchun biz maksimal ikkilik daraxtni qayta sozlash kerak.
Bu MAX-HEAPIFY (A, 1) ni chaqirishdir.
HEAPSORT( A )
1. BUILD MAX HEAP(‐ ‐ A )
2. for i ← length [ A ] downto 2
3. do exchange A[1] A[ i ]
4. heap size
‐ [A] ← heap size ‐ [A] -1
5. MAX HEAP
‐](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_30.png)
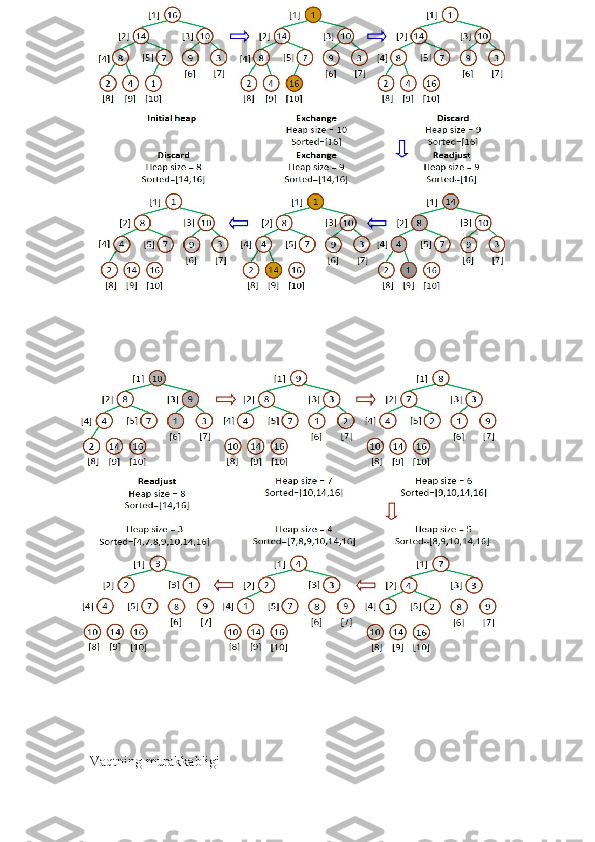
![ HEAPSORT protsedurasi O(nlgn) vaqt oladi
BUILD-MAX-HEAP-ga murojaat O(n) vaqt oladi
MAX-HEAPIFY ga har bir n−1 chaqiruv O(lgn) vaqtni oladi
Ustuvor navbatlarni massivlash
Massivlar ustuvor navbatlarni samarali amalga oshiradi.
Ikki xil ustuvor navbatlar mavjud: maksimal ustuvor navbatlar
va minimal ustuvor navbatlar.
Biz bu yerda maksimal ustuvor navbatlarni qanday amalga
oshirishga e'tibor qaratamiz, ular o'z navbatida max-massivlarga
asoslangan.
Ustuvor navbat - bu S ikkilik daraxtini saqlash uchun ma'lumotlar
tuzilmasi
elementlarning har biri kalit deb ataladigan tegishli qiymatga ega.
Ustuvor navbatlar
Maksimal ustuvorlik navbati quyidagi amallarni qo'llab-
quvvatlaydi.
INSERT(S, x): S to plamga x elementini kiritadi.ʻ
MAXIMUM(S): eng katta kalitli S elementini qaytaradi.
EXTRACT-MAX(S): S elementini olib tashlaydi va qaytaradi
eng katta kalit.
ORTISH-KEY (S, x, k): x element kalitining qiymatini
yangi qiymat k. k ≥ x ning joriy kalitini qabul qiling
qiymat
Maksimal elementni topish
MAXIMUM(S): eng katta kalitli S elementini qaytaradi.
Maksimal elementni olish oson: bu ildiz.
HEAP MAXIMUM(A)
‐
1. return A[1]
HEAP-MAXIMUM ning ishlash vaqti T(1)](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_32.png)
![Maksimal element chiqarilmoqda
EXTRACT-MAX(S): S elementini olib tashlaydi va qaytaradi
eng katta kalit.
HEAP EXTRACT MAX(A)‐ ‐
1. if heap size
‐ [A] < 1
2. then error “heap underflow”
3. max ← A[1]
4. A[1] ← A[ heap size
‐ [A]]
5. heap size
‐ [A] ← heap size ‐ [A]-1
6. MAX HEAPIFY(A, 1)
‐
7. return max
Tahlil: MAX-HEAPIFY uchun doimiy vaqtni belgilash vaqti.
HEAP-EXTRACT-MAX ning ishlash vaqti O(lgn).
Kalit qiymatini oshirish
ORTISH-KEY (S, x, k): x element kalitining qiymatini k ga
oshiradi.
k ≥ x ning joriy kalit qiymatini qabul qiling.
HEAP INCREASE KEY (A,
‐ ‐ i , key )
1. if key < A[ i ]
2. then error “new key is smaller thean current key”
3. A[ i ] ← key
4. While i > 1 and A[PARENT( i )] < A[ i ]
5. do exchange A[ i ] A[PARENT( i )]
6. i ← PARENT( i )
Tahlil: tugundan ildizgacha yangilangan yo l
ʻ
uzunligi O(lgn)ga ega.](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_33.png)
![Ikkilik daraxtga kiritish
INSERT(S, x): S to plamga x elementini kiritadi.ʻ
MAX HEAP INSERT(A)
‐ ‐
1. heap size
‐ [A]← heap size ‐ [A]+1
2. A[ heap size
‐ [A]←
3. HEAP INCREASE KEY(A,
‐ ‐ heap size ‐ [A], key )
Tahlil: HEAP-INCREASE-KEY uchun doimiy vaqtni belgilash
vaqti.
Ishlash vaqti O(lgn).
2.3 Heap-Sort algoritmini afzalliklari](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_34.png)


![hajmiga bog'liq va boshqa omillar biz saralashdan foydalanmoqchi
bo'lgan algoritmga ta'sir qiladi.
2.5 Heap-Sort algoritmini C++ dasturlash tilida ifodalanishi
C++ da Heap Sort tartiblash algoritmi
MAX-MASSIVLASH(A,i)
1- i<-chap[i]
2- r<-right[i]
3- if lA[i]
4- keyin eng katta<-1
5- boshqa eng katta<-i
6- if rA[eng katta]
7- keyin eng katta<-r
8- eng katta bo'lsa!=i
9- keyin A[i]<->A[eng katta] almashtiring
10- MAX-HEAPIFY[A,eng katta]
HOP-SART(A)
1- MAKS-MASSIV QURISH(A)
2- i<-uzunligi[A] uchun 2 gacha
3- A[1]<-> massiv o'lchami[A]-1 almashtiring
4- massiv o'lchami[A]<-massiv o'lchami[A]-1
5- MAKS-YUMLASH(A,1)
MAKS-MASSIV (A) QURISH
1- to p o lchami[A]<-uzunlik[A]ʻ ʻ
2- i<-(uzunlik[A]/2) uchun 1 tagacha
3- MAX-MASSIVLASH(A,i)](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_37.png)
![#include <iostream>
using namespace std;
void heapify(int arr[], int n, int i)
{
int largest = i;
int l = 2*i + 1;
int r = 2*i + 2;
//Agar chap uch ildizdan katta bo'lsa
if (l < n && arr[l] > arr[largest])
largest = l;
//Agar o'ng uch eng katta bo'lsa
if (r < n && arr[r] > arr[largest])
largest = r;
// Agar ildiz eng katta bo'lmasa
if (largest != i)
{
swap(arr[i], arr[largest]);
//Subdaraxtni rekursiv yig'ish
heapify(arr, n, largest);
}
}
void heapSort(int arr[], int n)
{
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
//Massivdan elementni birma-bir ajratib oling
for (int i=n-1; i>=0; i--)
{
//Joriy ildizni oxirigacha ko'chirish](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_38.png)
![swap(arr[0], arr[i]);
//Kamaytirilgan ikkilik daraxtda max heapify chaqirilmoqda
heapify(arr, i, 0);
}
}
//Masivni chop etish funksiyasi
void display(int arr[], int n)
{
for (int i = 0; i < n; i++)
{
cout << arr[i] << "\t";
}
cout << "\n";
}
int main()
{
int arr[] = {1, 14, 3, 7, 0};
int n = sizeof(arr)/sizeof(arr[0]);
cout << "Saralanmagan massiv \n";
display(arr, n);
heapSort(arr, n);
cout << "Saralangan massiv \n";
display(arr, n);
}
Chiqarish:
Saralanmagan massiv
1 14 3 7 0
Saralangan massiv](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_39.png)
![0 1 3 7 14
Vaqtning murakkabligi
C++ da massiv tartiblash uchun
Eng yaxshi
O(nlog n)
O'rtacha
O(nlog n)
Eng yomoni
O(nlog n).
2.6 Heap-Sort algoritmini Python dasturlash tilida ifodalanishi
Massiv tartiblash uchun Python dasturi
• Qiyinchilik darajasi : O'rta
Heapsort - bu ikkilik massiv ma'lumotlar tuzilishiga asoslangan
taqqoslashga asoslangan saralash usuli. Bu birinchi navbatda maksimal
elementni topib, maksimal elementni oxiriga qo'yadigan tanlash tartibiga
o'xshaydi. Qolgan element uchun xuddi shu jarayonni takrorlaymiz.
# Saralash ikkilik daraxtini amalga oshirish uchun Python dasturi
# i indeksida joylashgan pastki daraxtni yig'ish uchun.
# n - massiv hajmi
def heapify(arr, n, i):
largest = i # Eng kattani ildiz sifatida ishga tushirish
l = 2 * i + 1 # chap = 2 * i + 1
r = 2 * i + 2 # o'ng = 2 * i + 2
# Ildizning chap ildiz tuguni mavjudligini va mavjudligini tekshiring
# ildizdan katta
if l < n and arr[i] < arr[l]:
largest = l
# Ildizning to'g'ri ildiz tuguni mavjudligini va mavjudligini tekshiring
# ildizdan katta](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_40.png)
![if r < n and arr[largest] < arr[r]:
largest = r
# Agar kerak bo'lsa, ildizni o'zgartiring
if largest != i:
arr[i],arr[largest] = arr[largest],arr[i] # almashtirish
# Ildizni massivlang.
heapify(arr, n, largest)
# Berilgan o lchamdagi massivni saralash uchun asosiy funksiyaʻ
def heapSort(arr):
n = len (arr)
# Maxheap quring.
# Oxirgi ildiz-ona ((n//2)-1) bo'lgani uchun biz o'sha joydan
boshlashimiz mumkin.
for i in range(n // 2 - 1, -1, -1):
heapify (arr, n, i)
# Elementlarni birma-bir ajratib oling
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # ta almashtirish
heapify (arr, i, 0)
# Yuqoridagi sinov uchun haydovchi kodi
arr = [ 12, 11, 19, 5, 6, 7]
heapSort(arr)
n = len (arr)
print("Tartiblangan massiv")
for i in range(n):
print("%d" %arr[i]),
# Ushbu kod Mohit Kumra tomonidan kiritilgan
Chiqish:
Tartiblangan massiv 5 6 7 11 12 1](/data/documents/ed0326d4-d29a-4aa1-bfca-f4dd45051685/page_41.png)



Mundarija Kirish: ...................................................................................................................................................... 2 Raqamli texnologiyalarning zamonaviy dunyosida dasturlash turli xil kompyuterlar, gadjetlar va boshqa elektron qurilmalarning ishlashi uchun asos bo'lib xizmat qiladi. Va algoritmning blok diagrammasini tez va to'g'ri tarzda tuzish qobiliyati bu fanning asosidir. Bunday sxema asboblar tomonidan bajarilishi kerak bo'lgan jarayonlarning grafik modeli. Turli funktsiyalarni bajaradigan alohida funktsiya bloklaridan iborat. Algoritm – maʼlum bir turga oid masalalarni yechishda ishlatiladigan amallarning muayyan tartibda bajarilishi haqidagi aniq qoida (dastur). Kibernetika va matematikaning asosiy tushunchalaridan biri. Oʻrta asrlarda oʻnli sanoq tizimi boʻyicha toʻrt arifmetik amal bajariladigan qoidani Algaritm deb atashgan. "Bu qoidalarni matematikaga 9- asrda al-Xorazmiy tomonidan kiritilgan. Yevropada bunday qoidalar uning tug'ilgan yurtiga nisbatan lotinchalashtirilgan (Algoritmus yoki Algorithmus shaklida "algorizm" deyilgan), keyinchalik "algoritm"ga aylangan" (akademik A. N. Kolmogorov). Fanga "Yevklid algoritmi", "Gʻiyosiddin Koshiy algoritmi", "Laure algoritmi", "Markov algoritmi" deb ataluvchi algoritmlar maʼlum. Algoritm tushunchasi tobora kengayib borib, kibernetikaning nazariy va mantiqiy asosi hisoblangan algoritmlar nazariyasi paydo boʻldi. Oʻzbekiston Respublikasida bir necha ilmiy tadqiqot muassasalari va hisoblash markazlarida Algoritmdan foydalanish sohasida samarali ishlar olib borilmoqda. Masalan Oʻzbekiston Fanlar akademiyasi "Kibernetika" ilmiy ishlab chiqarish birlashmasida, Oʻzbekistondagi barcha universitetlarda, Toshkent davlat texnika universitetida, Oʻzbekiston Respublikasi Makroiqtisod va statistika vazirligi qoshidagi Hisoblash markazi va boshqa muassasalarda olib borilayo’tgan ishlar bunga misol boʻla oladi. ......................................................... 2 I-BOB. Algoritmlar, Graflar va Daraxtlar tushunchasi ............................................................................ 4 1.1 Algoritmni tasvirlash usullari. .......................................................................................................... 4 1.2.Algoritmning asosiy xossalari. .......................................................................................................... 5 1.3 Graflar nazariyasi va uning paydo bo’lishi ....................................................................................... 6 1.4 Daraxtlar haqida tushuncha ............................................................................................................. 8 1.5.Binar daraxtlar .................................................................................................................................. 9 II-BOB. Heap-Sort Algoritmi ................................................................................................................. 10 2.1.Heap-Sort algoritmining yaratilish tarixi ........................................................................................ 10 2.2.Heap-Sort algoritmini tuzilishi ....................................................................................................... 11 2.3 Heap-Sort algoritmini afzalliklari ................................................................................................... 34 2.4 Heap-Sort algoritmini kamchiliklari ............................................................................................... 36 2.5 Heap-Sort algoritmini C++ dasturlash tilida ifodalanishi ............................................................... 37 2.6 Heap-Sort algoritmini Python dasturlash tilida ifodalanishi .......................................................... 40 Xulosa ................................................................................................................................................... 42 Ushbu kurs ishida asosiy mavzu sifatida Heap Sort algoritmi yoritilgan. Dastavval algoritm tushunchasi uning paydo bo’lishi haqida malumot berilgan va yana graflar ikkilik daraxtlar haqida ham malumotlar keltirilgan. Keyin esa asosiy mavzu sifatida Heap Sort algoritmi haqida to’liq malumotlar keltirilgan qachon paydo bo’lgan , kim tomonidan kashf etilgan , algoritmning afzalliklari , kamchiliklari va yana algoritmning dasturlash tillarida qanday tuzilishi ko’rsatib natijalari bilan berilgan. ...................................................................................................................................... 42 Ushbu kurs ishi 48 listdan iborat bo’lib uch bobga bo’lib yoritilgan (Algoritmlar, Graflar va darahtlar, Heap Sort algoritmi) bo’lib unda xulosa va foydalanilgan adabiyotlar qismi mavjud. ........................ 42 Foydalanilgan adabiyotlar .................................................................................................................... 44 Foydalanilgan Internet saytlar ............................................................................................................. 44
Kirish : Raqamli texnologiyalarning zamonaviy dunyosida dasturlash turli xil kompyuterlar, gadjetlar va boshqa elektron qurilmalarning ishlashi uchun asos bo'lib xizmat qiladi. Va algoritmning blok diagrammasini tez va to'g'ri tarzda tuzish qobiliyati bu fanning asosidir. Bunday sxema asboblar tomonidan bajarilishi kerak bo'lgan jarayonlarning grafik modeli. Turli funktsiyalarni bajaradigan alohida funktsiya bloklaridan iborat. Algoritm – ma lum bir turga oid masalalarni yechishdaʼ ishlatiladigan amallarning muayyan tartibda bajarilishi haqidagi aniq qoida (dastur). Kibernetika va matematikaning asosiy tushunchalaridan biri. O rta asrlarda o nli sanoq tizimi bo yicha to rt arifmetik amal ʻ ʻ ʻ ʻ bajariladigan qoidani Algaritm deb atashgan. "Bu qoidalarni matematikaga 9-asrda al-Xorazmiy tomonidan kiritilgan. Yevropada bunday qoidalar uning tug'ilgan yurtiga nisbatan lotinchalashtirilgan (Algoritmus yoki Algorithmus shaklida "algorizm" deyilgan), keyinchalik "algoritm"ga aylangan" (akademik A. N. Kolmogorov). Fanga "Yevklid algoritmi", "G iyosiddin Koshiy algoritmi", "Laure algoritmi", "Markov ʻ algoritmi" deb ataluvchi algoritmlar ma lum. Algoritm tushunchasi ʼ tobora kengayib borib, kibernetikaning nazariy va mantiqiy asosi hisoblangan algoritmlar nazariyasi paydo bo ldi. O zbekiston ʻ ʻ Respublikasida bir necha ilmiy tadqiqot muassasalari va hisoblash markazlarida Algoritmdan foydalanish sohasida samarali ishlar olib borilmoqda. Masalan O zbekiston Fanlar akademiyasi "Kibernetika" ʻ ilmiy ishlab chiqarish birlashmasida, O zbekistondagi barcha ʻ universitetlarda, Toshkent davlat texnika universitetida, O zbekiston ʻ Respublikasi Makroiqtisod va statistika vazirligi qoshidagi Hisoblash markazi va boshqa muassasalarda olib borilayo’tgan ishlar bunga misol bo la oladi. ʻ
I-BOB. Algoritmlar, Graflar va Daraxtlar tushunchasi 1.1 Algoritmni tasvirlash usullari. Biror masalani kompyuterda yechish uchun, avval uning matematik modelini, keyin esa yechish algoritmi va dasturini tuzish kerak bo‘ladi. Ushbu uchlikda algoritm bloki muhim ahamiyatga ega. Endi algoritm tushunchasining ta’rifi va xossalarini bayon qilamiz. Masala yechimini cheklangan qadamlar natijasida hosil qiladigan, oldindan tayinlangan va aniq belgilangan qoidalar yoki buyruqlar ketma-ketligi algoritm deyiladi. Soddaroq qilib aytganda, algoritm bu - oldimizga qo‘yilgan masalani yechish uchun zarur bo‘lgan amallar ketma-ketligidir. Algoritm tuzish - bu dasturlashdir, algoritmni tuzuvchilar esa dasturchilardir. Algoritmlarning eng ko‘p uchraydigan turlari bilan tanishamiz. Algoritmning so‘zlar orqali ifodalanishi. Bu usulda ijrochi uchun beriladigan har bir ko‘rsatma jumlalar, so‘zlar orqali buyruq shaklida beriladi. Algoritmning formulalar bilan ifodalanish usulidan matematika, fizika, kimyo kabi aniq fanlardagi formulalarni o‘rganishda foydalaniladi. Bu usul ba’zan analitik ifodalash deyiladi. Algoritmlarning maxsus geometrik shakllar yordamida ifodalanishida masala yechish jarayoni aniq va ravon tasvirlanadi va bu ko‘rinish blok-sxema deyiladi. Algoritmning jadval ko‘rinishda berilishi . Algoritmning bunday ifodasidan ham ko‘p foydalanamiz. Masalan, maktabda qo‘llanib kelinayo’tgan to‘rt xonali matematik jadvallar yoki turli xil lotereyalar jadvali. Funksiyalarning grafiklarini chizishda ham algoritmlarning qiymatlari jadvali ko‘rinishlaridan foydalanamiz. Bu kabi jadvallardan foydalanish algoritmlari sodda bo‘lgani tufayli ularni o‘zlashtirib olish oson. Yuqorida ko‘rilgan algoritmlarni tasvirlash usullarining asosiy maqsadi, qo‘yilgan masalani yechish uchun zarur bo‘lgan amallar ketma-
ketligining eng qulay holatini aniqlash va shu bilan inson tomonidan dastur yozishni yanada osonlashtirishdan iborat. Aslida, dastur ham algoritmning boshqa bir ko‘rinishi bo‘lib, u insonning kompyuter bilan muloqotini qulayroq amalga oshirish uchun mo‘ljallangan. 1.2.Algoritmning asosiy xossalari. Algoritmning 5 ta asosiy xossasi bor. 1. Diskretlilik (Cheklilik). Bu xossaning mazmuni algoritmlarni doimo chekli qadamlardan iborat qilib bo‘laklash imkoniyati mavjudligida. Ya’ni uni chekli sondagi oddiy ko‘rsatmalar ketma-ketligi shaklida ifodalash mumkin. Agar kuzatilayo’tgan jarayonni chekli qadamlardan iborat qilib qo‘llay olmasak, uni algoritm deb bo‘lmaydi. 2.Tushunarlilik. Biz kundalik hayotimizda berilgan algoritmlar bilan ishlayo’tgan elektron soatlar , mashinalar, dastgohlar, kompyuterlar, turli avtomatik va mexanik qurilmalarni kuzatamiz. Ijrochiga tavsiya etilayo’tgan ko‘rsatmalar uning uchun tushinarli mazmunda bo‘lishi shart, aks holda, ijrochi oddiygina amalni ham bajara olmaydi. Bundan tashqari, ijrochi har qanday amalni bajara olmasligi ham mumkin.Har bir ijrochining bajarishi mumkin bo‘lgan ko‘rsatmalar yoki buyruqlar majmuasi mavjud, u ijrochining ko‘rsatmalar tizimi (sistemasi) deyiladi. Demak, ijrochi uchun berilayo’tgan har bir ko‘rsatma ijrochining ko‘rsatmalar tizimiga mansub bo‘lishi lozim. Ko‘rsatmalarni ijrochining ko‘rsatmalar tizimiga tegishli bo‘ladigan qilib ifodalay olishimiz muhim ahamiyatga ega. Masalan, quyi sinfning a’lochi o‘quvchisi "son kvadratga oshirilsin" degan ko‘rsatmani tushunmasligi natijasida bajara olmaydi, lekin "son o‘zini o‘ziga ko‘paytirilsin" shaklidagi ko‘rsatmani bemalol bajaradi , chunki u ko‘rsatma mazmunidan ko‘paytirish amalini bajarish kerakligini anglaydi. 3. Aniqlik . Ijrochiga berilayo’tgan ko‘rsatmalar aniq va mazmunli bo‘lishi zarur. Chunki ko‘rsatmadagi noaniqliklar mo‘ljaldagi
