IKKI CHIZIQNI KESISHISH UCHUN TEKSHIRISH ALGORITMLARI





![17. int x = x0, y = y0;
18. agar (belgisi == -1)
19. {
20. qil (
21. f + = A * belgisi;
22. agar (f> 0)
23. {
24. f - = B * belgisi;
25. y + = belgisi;
26. }
27. x - = belgisi;
28. z [y] [x] = "*";
29. }
30. boshqa
31. {
32. qil (
33. f + = B * belgisi;
34. agar (f> 0) (
35. f - = A * belgisi;
36. x - = belgisi;
37. }
38. y + = belgisi;
39. z [y] [x] = "*";
40. ) esa (x! = x1 || y! = y1);
41. }
42. }
43. int main ()
44. {
45. const int SIZE = 25; // maydon hajmi
46. int x1, x2, y1, y2;
47. char ** z;
48. z = yangi belgi *;
49. uchun (int i = 0; i< SIZE; i++)
50. {
51. z [i] = yangi belgi;
52. uchun (int j = 0; j< SIZE; j++)
53. z [i] [j] = "-";
54. }
55. kut<< "x1 = " ; cin >> x1;
56. kut<< "y1 = " ; cin >> y1;
57. kut<< "x2 = " ; cin >> x2;
58. kut<< "y2 = " ; cin >> y2;](/data/documents/153f21f9-9de4-48d8-b98a-25b3aece1ffa/page_6.png)
![59. Brezenhem (z, x1, y1, x2, y2);
60. uchun (int i = 0; i< SIZE; i++)
61. {
62. uchun (int j = 0; j< SIZE; j++)
63. kut<< z[i][j];
64. kut<< endl;
65. }
66. cin.get (); cin.get ();
67. qaytarish 0;
68. }
Bresenxem algoritmi nazorat vazifalarida ham ishlatilishi mumkin, masalan,
quvvatni yoki aylanish tezligini tartibga solish uchun. Bunday holda, gorizontal o'q
vaqt o'qi bo'lib, ko'rsatilgan qiymat to'g'ri chiziqning burchagi koeffitsientini
o'rnatadi.
Agar kosmik diskret bo'lmasa, nega Axilles toshbaqani quvib o'tadi? Agar kosmik
diskret bo'lsa, unda zarrachalar Bresenhem algoritmini qanday amalga oshiradi?
Men uzoq vaqt davomida umuman olam nimani anglatishi va uning qonunlari
haqida o'ylardim. Ba'zida o'sha Vikipediyadagi ba'zi fizik hodisalarning tavsiflari,
bu sohadan unchalik uzoq bo'lmagan odam uchun ham tushunarsiz bo'lib qolishi
uchun chalkashtirib yuboradi. Bundan tashqari, menga o'xshaganlar - hech
bo'lmaganda, bu hududdan juda uzoqda bo'lganlar uchun omadim kelmadi. Ammo,
men dasturchi sifatida deyarli har kuni biroz boshqacha tekislikka duch kelaman -
algoritmlar. Va bir marta, konsolda 2 -darajali fizikaning bir xil ko'rinishini amalga
oshirish jarayonida, men o'yladim: "Ammo koinot, aslida, noma'lum o'lchovli
konsoldir. Bu konsol ekranida chiziqli harakatlanish uchun zarrachalar Bresenxem
algoritmini bajarmasligi kerak deb o'ylashga asos bormi? " Va hech qanday sabab
yo'qdek tuyuladi.
Bresenhamning algoritmi umuman nimaga bog'liqligi, uning fizikaga qanday
aloqasi borligi va bu uning talqiniga qanday ta'sir qilishi mumkinligi bilan qiziqqan
har bir kishini mushuk ostida xush kelibsiz. Ehtimol, siz u erda parallel
olamlarning mavjudligini bilvosita tasdiqini topasiz. Yoki hatto ichki uyalar ham
bor.
Bresenhem algoritmi qo’llanilishi.
Oddiy qilib aytganda , daftar qog ' oziga bir hujayrali qalinlikdagi chiziq chizish
uchun ketma - ket ketma - ket hujayralarni bo ' yash kerak bo ' ladi . Daftar varag ' i
tekisligi hujayralarda diskret , deylik , siz qo ' shni katakchalarning ikkita qo ' shni
yarmini bo ' yab bo ' lolmaysiz va 0,5 ofsetli hujayraning ustidan bo ' yalgan deb ayta
olmaysiz , chunki diskretlik bunday harakatning yo ' l qo ' yilmasligidan iborat . .](/data/documents/153f21f9-9de4-48d8-b98a-25b3aece1ffa/page_7.png)









![D uchun< 0 расстояние от окружности до диагонального пикселя больше, чем
до горизонтального . Aksincha, agar d > 0, gorizontal pikselgacha bo'lgan masofa
katta. Shunday qilib,
d da<= 0 выбираем m H в (x i , + 1, у i - 1)
d> 0 uchun biz m D ni tanlaymiz (x i, + 1, y i - 1)
E = 0 bo'lsa, aylanadan ikkala pikselgacha bo'lgan masofa bir xil bo'lsa, gorizontal
qadamni tanlang.
E qiymatini baholash uchun zarur bo'lgan hisob -kitoblar sonini kamaytirish
mumkin, agar 1 -holatda
(x i + 1) 2 + (y i) 2 -R 2> = 0, (x i + 1) 2 + (y i -1) 2 -R 2< 0
diagonal piksel bo'lgani uchun (x i, + 1, da i - 1) har doim aylana ichida yotadi va
gorizontal (x i, + 1, da i) - undan tashqarida. Shunday qilib, e ni formula bo'yicha
hisoblash mumkin
d = (x i + 1) 2 + (y i) 2 -R 2 + (x i + 1) 2 + (y i -1) 2 -R 2
(Y i) 2 atamaning kvadratini to'ldirish va ayirish - 2y i + 1 beradi
d = 2 [(x i + 1) 2 + (y i -1) 2 -R 2] + 2y i - 1
Kvadrat qavs ichida e i ta'rifi va uning o'rnini bosadi
d = 2 (e i + y i) - 1
ifodasini ancha soddalashtiradi.
2 -rasmni ko'rib chiqing. 11 va gorizontal piksel (x i, + 1, y i) bu erda tanlanishi
kerakligini unutmang, chunki y - monoton kamayuvchi funktsiya. E
komponentlarini tekshirish shuni ko'rsatadiki
(x i + 1) 2 + (y i) 2 -R 2< 0, (x i + 1) 2 + (y i -1) 2 -R 2< 0
chunki 2 -holatda gorizontal (x i, + 1, y i) va diagonal (x i, + 1, y i -1) piksellar
aylana ichida yotadi. Shuning uchun, d< 0, и при использовании того же самого
критерия, что и в случае 1, выбирается пиксел (x i , + 1, у i).
Agar e i> 0 bo'lsa, u holda diagonal nuqta (x i, + 1, y i -1) aylanadan tashqarida,
ya'ni bu 3 -va 4 -holatlar. 11. Bunday vaziyatda (x i, + 1, y i -1), yoki (x i, y i -1)
pikselni tanlash kerakligi aniq. . Oldingi holatni tahlil qilish singari, tanlov
mezonini 3 -holatni ko'rib chiqish va aylanadan diagonal m D va vertikal m V
pikselgacha bo'lgan masofalar kvadratidagi farqni tekshirish orqali olish mumkin.](/data/documents/153f21f9-9de4-48d8-b98a-25b3aece1ffa/page_19.png)
![ya'ni d " = | (x i + 1) 2 + (y i -1) 2 -R 2 | -| (x i) 2 + (y i -1) 2 -R 2 |
D uchun " < 0 aylanadan vertikal pikselgacha bo'lgan masofa (x i, y i -1) katta va
siz pikselga diagonal qadam tanlashingiz kerak (x i, + 1, y i -1). Aksincha, d " > 0
aylanadan diagonal pikselgacha bo'lgan masofa katta va siz pikselga vertikal
harakatni tanlashingiz kerak (x i, y i -1). Shunday qilib,
d da " <= 0 m D ni tanlang (x i +1, y i -1)
d da " > 0 m V ni tanlang (x i, y i -1)
Bu erda, d holatida " = 0, ya'ni masofalar teng bo'lganda, diagonal qadam
tanlanadi.
E komponentini tekshirish " buni ko'rsatadi
(x i) 2 + (y i -1) 2 -R 2> = 0, (x i + 1) 2 + (y i -1) 2 -R 2< 0
chunki 3 -holat uchun diagonal piksel (x i +1, y i -1) aylanadan tashqarida, vertikal
piksel (x i, y i -1) uning ichida joylashgan. Bu bizga e yozishga imkon
beradi " sifatida
d " = (x i +1) 2 + (y i -1) 2 -R 2 + (x i) 2 + (y i -1) 2 -R 2
(X i) 2 kvadratini 2x i + 1 qo'shish va ayirish orqali to'ldirish beradi
d " = 2 [(x i +1) 2 + (y i -1) 2 -R 2] - 2x i - 1
D i ta'rifidan foydalanib, ifoda shaklga keltiriladi
d " = 2 (e - x i )- 1
Endi, 4 -holatni ko'rib chiqib, yana bir bor ta'kidlaymizki, vertikal piksel (x i, y i -
1) tanlanishi kerak, chunki y -monoton kamayuvchi funktsiya. NS.
D komponentlarini tekshirish " 4 -holat shuni ko'rsatadiki
(x i +1) 2 + (y i -1) 2 -R 2> 0, (x i) 2 + (y i -1) 2 -R 2> 0
chunki ikkala piksel ham doiradan tashqarida. Shuning uchun, e " > 0 va 3 -holat
uchun ishlab chiqilgan mezondan foydalanganda m V ni to'g'ri tanlash .
Rasmdagi 5 -holatni tekshirish kifoya. 11, bu diagonal piksel (x i, y i -1) aylanada
yotganda sodir bo'ladi, ya'ni d i = 0. E komponentalarini tekshirish shuni
ko'rsatadiki,
(x i +1) 2 + (y i) 2 -R 2> 0](/data/documents/153f21f9-9de4-48d8-b98a-25b3aece1ffa/page_20.png)

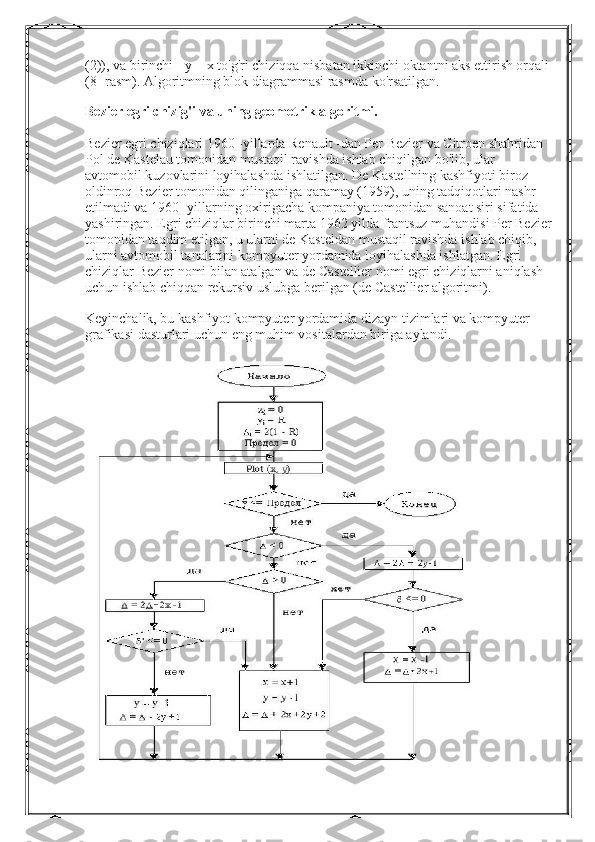





MAVZU: IKKI CHIZIQNI KESISHISH UCHUN TEKSHIRISH ALGORITMLARI. MUNDARIJA Kirish. ........................................................................................................................................................... 2 Bresenhem algoritmi ................................................................................................................................... 3 Bresenhem algoritmi qo’llanilishi. ............................................................................................................... 7 Bresenhem algoritmining asosiy g'oyasi. ................................................................................................... 11 Bresenxem algoritmidagi xato grafigi. ....................................................................................................... 12 Birinchi oktant uchun segmentni rastrlash uchun Bresenhem algoritmi ................................................... 13 Bresenhem algoritmining blok diagrammasi. ............................................................................................ 14 General Bresenhem algoritmi. ................................................................................................................... 15 Umumlashtirilgan Bresenhem algoritmi uchun misollar tahlili. ................................................................. 16 Doira hosil qilish uchun Bresenhem algoritmi. .......................................................................................... 17 Birinchi oktantdagi yoydan to`liq aylana hosil bo`lishi. .............................................................................. 17 ................................................................................................................................................................... 18 Birinchi chorakda aylana hosil qilish uchun Bresenhemning bosqichma-bosqich algoritmi ...................... 21 Bezier egri chizig'i va uning geometrik algoritmi. ...................................................................................... 22 Bezier egri chiziqlarining turlari ................................................................................................................. 23 Kompyuter grafikasida dastur .................................................................................................................... 24 Xulosa. ...................................................................................................................................................... 24 Foydalanilgan adabiyotlar. ......................................................................................................................... 26
Kirish . Algoritm so`zi barchamizga ma`lum bo`lganidek, vatandoshimiz Muhammad ibn Muso al-Xorazmiyning ismini yevropacha talaffuzidan kelib chiqqan. Demak, hozirda keng foydalanilayotgan algoritmlashning asosi bizning Vatanimizdan boshlangan. Maktab informatika kursidan ma`lumki, algoritm bu – ma`lum masalani hal qilish uchun bajarish kerak bo`lgan amallar ketma-ketligi. O`sha mashhur choy damlash algoritmidan chekingan holda hayotiy misol keltiramiz. Hayotda eng ko`p bo`ladigan holatimiz bu uyqu. Ko`pchilik rejim bilan uxlaydi , ya`ni uxlashga ma`lum bir vaqtni belgilagan. Misol uchun siz uxlashga yotish uchun 22:00ni tanladingiz. Har safar soatga qaraganingizda uxlash vaqti bo`lgan yoki bo`lmaganini tekshirasiz. Miyangizda esa quyidagi jarayon bo`ladi: Bu oddiy uyquga yotish algoritmi edi. Hayotda o`zimiz bilmagan holatda algoritmlardan foydalanamiz. Miyamiz juda tez ishlagani sabab qadamlar ketma- ketligi haqida o`ylab ko`rmaymiz. Endi maqolamizning asosiy qismi, dasturlashda algoritmlashga o`tamiz. Dasturlashda algoritm bu – masalani yechish uchun bajarilishi kerak bo`lgan amallar ketma-ketligini kodga o`girilgan varianti. Bunda masalani yechish uchun miyamizda kechayotgan jarayonni kompyuter tushunadigan qilib yozish talab etiladi. Algoritmlashning asosi matematika hisoblanadi. Bunda fikrlash muhim rol o`ynaydi. So`zimni quyidagicha isbot qilaman. Dasturlash sanoatida gigant korporatsiya hisoblangan Microsoftning asoschisi Bill Geytsning shunday so`zlari dasturchilar orasidda mashhur:"Qo`shish va ayirishni biladigan har qanday inson dasturchi bo`la oladi". Bu so`zlarni mag`zini chaqish uchun sizlarni boshlang`ich sinflarga qaytishga taklif etaman. Har birimiz boshlang`ich sinflarda qo`shish va ayirish amallarini o`rgangan edik. Ko`pchilik buni barmoqlari orqali bajargan. Chunki barmoqlar 10ta va raqamlarni qo`shish va ayirishda qo`l keladi. Keyinchalik matematik evolutsiyamiz sonlar bilan qo`shish va ayirish amallarini bajarish bosqichiga yetib keladi. Bu rivojlanish jarayoni yangi amallar bilan boyidi va endi bir xil raqamlarni bir necha marta qo`shishni osonlashtirish uchun ko`paytirish jadvalini o`rgandik. E`tibor bering, ko`paytirish algoritmi qo`shish algoritmining asosiga qurilgan. Rivojlanishimiz davom etib, endilikda qoldiqli bo`lish va shu kabi murakkabroq amallarga o`tamiz. Maktabni bitirish vaqtida esa juda murakkab amallarni ham bajara oladigan darajada bo`lamiz. Ana ko`rdingizmi, hamma murakkab amallarning asosi qo`shish va ayirishdan boshlanadi. U yog`i esa fikrlash doirangiz kengligiga bog`liq. Demak, dasturlashdagi asosiy masalalar matematik fikrlashga bog`liq.
Algoritmlashning asosiy shartlaridan biri bu – dasturning ishlash tezligi. Kod qanchalik optimal bo`lsa, dastur shuncha tez ishlaydi. Dastur tezligini pasaytiruvchi omillar bu – loop, ya`ni takrorlanishlar. Sikl ichida sikl ochish yoki sikl ichida shart tekshirish dastur tezligini ma`lum darajada pasaytiradi. Hayotiy misol keltiraman: 7ta 45ni bir biriga qo`shing. Har birini alohida qo`shib chiqish uchun vaqt talab etiladi. Ya`ni 7 marta bir xil amalni bajarish kerak. Xuddi shuni ko`paytirish amali orqali kamroq vaqt sarflab amalga oshirish mumkin. Har birimiz arifmetik progressiya haqida tushunchaga egamiz. Hadlari bir biridan ma`lum d songa farq qiladigan sonli ketma-ketlik. Shuni nta hadi yig`indisini toppish uchun n marta har safar yangi hadni topish va uni oldingi sonlar yig`indisiga qo`shish talab etiladi. Bu esa juda ko`p vaqt talab qiladi. Aynan shu muammo matematikada oddiy formula orqali hal etilgan. Bu muammoni hal etish formulasi esa albatta tafakkur mahsuli hisoblanadi. Siz ham yuqori darajali masalalarni yechishda ana shunday ixtirolar qilasiz yoki boshqa ixtirolardan foydalanasiz. Dasturlashda algoritmlashning asosan 4 turi mavjud: 1.Saralash 2.Qidirish 3.Grafiklar 4.Stringlar Ularning har biriga keyingi maqolalarimizda alohida to`xtalib o`tishga harakat qilamiz. Hozir esa oddiy algoritmlaning kodga o`girilish jarayonini ko`rib chiqamiz. Bresenhem algoritmi Ikki chiziqni kesishish uchun tekshirish algoritmlaridan biri haqida aytsak bu- Bresenhem algoritmidir.Bresenxem algoritmi Jek E. Bresenxem tomonidan 1962 yilda taklif qilingan va u tekislikda nuqtalari bo'lgan raqamlarni chizish uchun mo'ljallangan. Bu algoritm ekranda chiziqlar chizish uchun kompyuter grafikasida keng qo'llaniladi. Algoritm ikki o'lchovli rastrning qaysi nuqtalarini bo'yash kerakligini aniqlaydi. C = y1 ∙ x2-y2 ∙ x1 Koordinatali har qanday raster nuqtasi uchun ( xi;yi) qiymat funktsiyasi Bresenhem algoritmining grafik talqini rasmda ko'rsatilgan .
Bresenhem algoritmi yordamida tekislikda to'g'ri chiziq segmentlarini chizish uchun biz to'g'ri chiziq tenglamasini umumiy shaklda yozamiz. f (x, y) = Ax + By + C = 0 bu erda koeffitsientlar A va B koeffitsientlar bilan ifodalanadi k va b to'g'ri chiziq tenglamalari. Agar to'g'ri chiziq koordinatali ikkita nuqta orqali o'tsa ( x1;y1) va ( x2;y2), keyin to'g'ri chiziq tenglamasining koeffitsientlari formulalar bilan aniqlanadi A = y2-y1, B = x1-x2 f (xi, yi)= 0, agar nuqta to'g'ri chiziqda bo'lsa f (xi, yi)> 0, agar nuqta to'g'ri chiziq ostida bo'lsa f (xi, yi) qayerda i- ko'rsatiladigan nuqta raqami. Shunday qilib, qaysi nuqtalarni hal qilish usullaridan biri P. yoki Q(rasmga qarang) keyingi bosqichda ko'rsatiladi, bu segmentning o'rtasini solishtirish | P-Q | funktsiya qiymati bilan f (x, y)... Agar qiymat bo'lsa f (x, y) chiziq segmentining o'rta nuqtasidan pastda joylashgan | P-Q |, keyin keyingi ko'rsatiladigan nuqta nuqta bo'ladi P., aks holda - nuqta Q .
Funktsiyaning ortishini yozamiz ∆f = A∆x + B∆y Nuqtani koordinatalar bilan ko'rsatgandan so'ng (xi, yi) ko'rsatiladigan keyingi nuqta aniqlanadi. Buning uchun o'sish ko'rsatkichlari taqqoslanadi Δ x va Yy, mos keladigan koordinata bo'ylab harakatning mavjudligi yoki yo'qligini tavsiflaydi. Bu o'sish 0 yoki 1 bo'lishi mumkin. Shuning uchun biz nuqtadan o'ngga harakat qilsak, biz nuqtadan o'ngga va pastga siljiganimizda ∆f = A + B, biz bir nuqtadan pastga siljiganimizda, demak Biz segment boshining koordinatalarini bilamiz, ya'ni aniq to'g'ri chiziqda yotadigan nuqta. Biz birinchi nuqtani qo'yamiz va qabul qilamiz f= 0. Siz joriy nuqtadan ikki qadam - vertikal (gorizontal) yoki diagonal bo'yicha bitta pikselga o'tishingiz mumkin. Vertikal yoki gorizontal harakatlanish yo'nalishi qiyalik nisbati bilan belgilanadi. Nishab burchagi 45º dan past bo'lsa va | A |<|B| har bir qadamda harakat gorizontal yoki diagonalda amalga oshiriladi. Nishab burchagi 45º dan yuqori bo'lsa, har bir qadamda harakat vertikal yoki diagonalda amalga oshiriladi. Shunday qilib, egilgan segmentni chizish algoritmi quyidagicha: C ++ ilovasi : 1. #qo'shing 2. std nomlar maydonidan foydalanish; 3. bo'sh Brezenhem (char ** z, int x0, int y0, int x1, int y1) 4. { 5. int A, B, belgisi; 6. A = y1 - y0; 7. B = x0 - x1; 8. agar (abs (A)> abs (B)) belgisi = 1; 9. else belgisi = -1; 10. int signa, belgi; 11. agar (A.< 0) signa = -1; 12. else signa = 1; 13. agar (B.< 0) signb = -1; 14. else signb = 1; 15. int f = 0; 16. z = "*";
