logo
  1. Bosh sahifa
  2. Diplom ishlar
  3. Umumiy
  4. Иссиқлиқ ўтказувчанлик ва конвекция ҳисобидан иссиқлик кўчиши жараёнининг баьзи математик моделларини тадқиқ этиш

Иссиқлиқ ўтказувчанлик ва конвекция ҳисобидан иссиқлик кўчиши жараёнининг баьзи математик моделларини тадқиқ этиш

Yuklangan vaqt:

13.08.2023

Ko'chirishlar soni:

0

Hajmi:

15162.5 KB
Ko'chirib olish
Иссиқ ли қ ў тказувчанлик ва конвекция ҳ исобидан исси қ лик к ў чиши жараёнининг баьзи математик моделларини тад қ и қ этиш МУНДАРИЖА Кириш………………………………….………………………………………..3 I БОБ. Чекли элементлар усули ва унинг баьзи бир чегаравий масалаларга тадбиқи….........................…………….………………… ………………….. ....7 II БОБ. Иссиқлик ўтказувчанлик назариясининг асосий тушунчалари ………………………….……………………… ………… …….… ………. …..22 III БОБ. Иссиклик утказувчанлик ва конвекция хисобидан иссиклик кучиши жараёнининг баьзи математик моделларини тадкик этиш ………………………………………………………………..…...…… ..53 ХУЛОСА………..……………………………………… . ………………..…...78 АДАБИЁТЛАР……………………………………………… . ……………......79 ИЛОВАЛАР.......................................................................................................83 1 2 КИРИШ Чекли элементлар усули физика ва техникада учрайдиган дифференциал тенгламаларни сонли ечиш усули ҳисобланади. Бу усулнинг пайдо бўлиши космик тадқиқотларни ҳал қилиш муаммолари билан боғлиқ (1950). Бу иш биринчи марта Тёрнер, Клуж, Мартин ва Топп томонидан нашр э тилган [4]. Бу бошқа ишлар нинг пайдо бўлиши га туртки бўлди ; чекл и э лемент лар усули ни қурилиш механикаси ва туташ муҳитлар механикасига татбиқ қилинган бир қатор мақолалар чоп э тил ди. Усулни назарий асослаш учун 1963 йил Мелош [2] муҳим ҳисса қушди. У чекли элементлар усулини Рэлей-Ритц усулининг вариантларидан бири эканлигини кўрсатди. Қурилиш механикасида чекли элементлар усули потециал энергияни минималлаштириш орқали масалани мувозанатнинг чизиқли тенгламалар системасига келтириш имконини беради. Чекли элементлар усулининг минималлаштиришга боғлиқлиги унинг техниканинг бошқа соҳаларидаги муаммоларини ҳал қилишда фойдаланишга олиб келди. Усул Лаплас ёки Пуассон тенгламалари билан тавсифланган муаммоларга нисбатан ҳам қўлланилди. Бу тенгламаларни ечиш ҳам бирор функционални минималлаштириш билан боғлиқ. Дастлабки нашрларда [6, 7] чекли элементлар усули ёрдамида иссиқлик тарқалиш масалалари ечилди. Сўнгра бу усул гидромеханика муаммоларига, хусусан, ғовакли муҳитда суюқлик оқими муаммосига нисбатан қўлланилди. Қурилиш механикаси, иссиқлик тарқалиши, гидромеханика масалаларида элементларни аниқловчи тенгламалар вазнли тафовутлар усулининг вариантларидан бири бўлган Галёркин ёки энг кичик квадратлар усули ёрдамида осонгина ҳосил қилиш мумкинлиги исботлангандан [3, 8] сўнг чеклиэлементлар усулининг қўлланиш соҳаси сезиларли даражада кенгайди. Бу фактнинг ўрнатилиши чекли элементлар 3 усулини назарий асослаш учун муҳим рол ўйнади натижада, бу усулни ихтиёрий дифференциал тенгламани ечишга қўллаш имконини берди. Шундай қилиб чекли элементлар усули қурилиш механикаси муаммоларини сонли ечиш усулидан дифференциал тенгламаларни ёки дифференциал тенгламалар системасини сонли ечишнинг умумий усулига айланди. Бу ривожланишга тезкор сонли ҳисоблаш машиналарининг мукамаллашуви ҳисобига 15 йил давомида эришилди. Тадқиқоднинг мақсади. Ушбу диссертациянинг мақсади чекли элементлар усулининг бир ўлчовли, икки ва уч ўлчовли иссиқлик ўтказувчанлик масалалари билан боғлиқ бўлган қирраларини мухокама қилишдан иборат. Чекли элементлар усулининг асослари билан бирга ушбу методнинг ЭҲМда бажариш масалалари ҳам қаралади. Тадқиқод масаласи. Диссертация ишида иссиқлик ўтказувчанлик масалаларига доир мақсад ва вазифалардан келиб чиқиб mathcad математик пакетидан фойдаланиб қуйидаги масалалар тадқиқ қилинади : 1. Бирор жисмга киритилаётган ёки ундан чиқаётган иссиқлик миқдорини температура тақсимоти берилганда ҳисоблаш. 2. Температура майдони кучланиш тақсимотига таьсир қилади. Температура градиенти мавжуд ва барча йўналишлар бўйича эркин тарқала олмайдиган ҳар бир жисмда температура кучланиши вужудга келади. Бу кучланишни айланувчи механизмлар (м.н реактив двигателлар ёки буғ генераторлари)ни лойихалаштириш пайтида албатта ҳисобга олиш зарур. 3. Температура кучланишини ҳисобга олиш учун энг аввало жисмдаги температура тақсимотини аниқлаш керак. Тадқиқоднинг обьекти ва предмети. Иссиқлик инсон ҳаётида, жумладан унинг организмининг фаол ишлашида муҳим рол ўйнайди. Озиқ-овқат таркибида бўлган кимёвий энергиянинг бир қисми иссиқликка 4 айланади ва бунинг натижасида инсон жисмсининг температураи 37 атрофида сақлаб турилади. Инсон жисмидаги температура баланси атроф муҳитга ҳам боғлиқ ва инсонлар қишда ишлаб чиқариш ва яшаш хоналарини иситиш учун ва ёзда совутиш учун кўп энергия сарфлашга мажбур бўлишади. Бу энергиянинг кўп қисмини иссиқлик машиналари, масалан қозон қурилмалари ва ёқилғи қазилмалари (кўмир, нефт)да ишлайдиган ва электр энергияси ишлаб чиқарадиган электростанцияларнинг буғ трубиналари етказиб беради. Иссиқлик алмашинуви ёки иссиқлик узатиш – бу жисм ичидаги ёки температуралар фарқига эга бўлган бир жисмдан иккинчи жисмга иссиқликни узатиш жараёнидир. Иссиқликни узатиш моддаларнинг хусусиятларига, температуралар фарқига ва табиатнинг экспериментал ўрнатилган қонунларига бўйсунади. Самарали ишлайдиган иссиқлик ёки совутиш тизимларини, ҳар хил двегателларни энергия қурилмаларини иссиқлик изоляция тизимларини яратиш учун иссиқлик узатишнинг талабларини билиш керак. Баьзи холларда иссиқлик алмашинувига эҳтиёж кам (космик кемаларда), баьзи холларда эса эҳтиёж кўп сезилади(буғ қозонлари, ошхона идишлари). Тадқиқод усуллари. Чекли элементлар усулининг минималлаштириш процедураси билан боғлиқлиги уни техниканинг бошқа соҳалардаги масалаларни ечишда ҳам кенг қўлланилишига олиб келди. Бу Лаплас усули ёки Пуассон тенгламалари билан тавсифланган масалаларга ҳам қўлланилади. Шу билан бирга бу тенгламаларни ечиш бирор функционални минималлаштириш билан боғлиқдир. Дастлабки нашрларда [6,7] чекли элементлар усули ёрдамида иссиқлик тарқалиш масалаларига тадбиқ қилинди. Сўнгра бу усул гидромеханика масалаларига, хусусан ғовак жисмларда суюқликни оқиш масалаларига қўлланила бошланди. 5 Тадқиқод натижаларининг илмий ва амалий аҳамияти. Тадқиқод назарий жиҳатдан ҳисоблаш усулларининг бир соҳасидир. Бу натижалардан физикада, гидромеханикада иссиқлик узатиш масалаларида фойдаланиш мумкин. Кўрилган мисоллардан амалиёт ва лаборатория машғулотларида ҳам фойдаланиш мумкин. Диссертациянинг таркиби ва ҳажми. Диссертация иши кириш қисми, учта боб, хулоса ва фойдаланилган адабиётлардан иборат. Ишнинг умумий ҳажми 77 бет. Адабиётлар рўйхатида _____ номдаги адабиётлар келтирилган. Биринчи бобда чекли элементлар усулининг асосий жиҳатлари ва унинг баьзи бир чегаравий масалаларга тадбиқлари қаралган: 1. Соҳани дискретлаштириш ; элементлар ва тугун нуқталарини аниқлаш . 2. Алоҳида элемент учун элемент (шакл) функцияларини аниқлаш . 3. Э лемент функцияларидан бутун соҳада аниқланган бўлакли-узлуксиз функцияни ҳосил қилиш. Иккинчи бобда иссиқлик ўтказувчанлик назариясининг асосий тушунчалари ва масалалари келтирилган. Учинчи бобда иссиклик ўтказувчанлик ва конвекция ҳисобидан иссиклик кўчиши жараёнининг баьзи математик моделларини тадкик этиш. Иловада диссертация ишида қаралган масалаларни ечишда қўлланилган ҳисоблаш дастурлари келтирилган. Бу ҳисоблаш дастурлари ўқув мақсадлари учун яратилган ва мураккаб масалаларни ечиш учун етарли эмас. 6 I БОБ. ЧЕКЛИ ЭЛЕМЕНТЛАР УСУЛИ ВА УНИНГ БАЬЗИ БИР ЧЕГАРАВИЙ МАСАЛАЛАРГА ТАДБИҚИ Чекл и элемент лар усули физика ва техникада учрайдиган дифферен ц иал тенгламалар ни сон л и ечиш усули ҳисобланади . Бу усулнинг пайдо бўлиши космик тадқиқотлар ни ҳал қилиш муаммо лари билан боғлиқ (1950). Бу иш биринчи марта Тёрнер, Клуж, Мартин ва Топп томонидан нашр э тилган [4]. Бу иш лар бошқа ишлар нинг пайдо бўлиши га туртки бўлди ; чекл и э лемент лар усули ни қурилиш механикаси ва туташ муҳитлар механикасига татбиқ қилинган бир қатор мақолалар чоп э тил ди. Усулни назарий асослаш учун 1963 йил Мелош [2] муҳим ҳисса қушди. У чеклиэлементлар усулиниРэлей-Ритц усулининг вариантларидан бири эканлигини кўрсатди. Қурилиш механикасида чекли элементлар усули потециал энергияни минималлаштириш орқали масалани мувозанатнинг чизиқли тенгламалар системасига келтириш имконини беради. Чекли элементлар усулининг минималлаштиришга боғлиқлиги унинг техниканинг бошқа соҳаларидаги муаммоларини ҳал қилишда фойдаланишга олиб келди. Усул Лаплас ёки Пуассон тенгламалари билан тавсифланган муаммоларга нисбатан ҳам қўлланилди. Бу тенгламаларни ечиш ҳам бирор функционални минималлаштириш билан боғлиқ. Дастлабки нашрларда [6, 7] чекли элементлар усули ёрдамида иссиқлик тарқалиш масалалари ечилди. Сўнгра усул гидромеханика муаммоларига, хусусан, ғовакли муҳитда суюқлик оқими муаммосига нисбатан қўлланилди. Қурилиш механикаси, иссиқлик тарқалиши, гидромеханика масалаларида элементларни аниқловчи тенгламалар вазнли тафовутлар усулининг вариантларидан бири бўлган Галёркин ёки энг кичик квадратлар усули ёрдамида осонгина ҳосил қилиш мумкинлиги исботлангандан [3, 8] сўнг чекли элементлар усулининг қўлланиш соҳаси 7 сезиларли даражада кенгайди. Бу фактнинг ўрнатилиши чекли элементлар усулини назарий асослаш учун муҳим рол ўйнади натижада, бу усулни ихтиёрий дифференциал тенгламани ечишга қўллаш имконини берди. Шундай қилиб чекли элементлар усули қурилиш механикаси муаммоларини сонли ечиш усулидан дифференциал тенгламаларни ёки дифференциал тенгламалар системасини сонли ечишнинг умумий усулига айланди. Бу ривожланишга тезкор сонли ҳисоблаш машиналарининг мукамаллашуви ҳисобига 15 йил давомида эришилди. 1.1. Чекл и э лемент лар усулининг асосий концепцияси. Чекли элементлар усулининг асосий ғояси шундан иборатки, исталган узлуксиз миқдорни, масалан: температура, босим ва кўчишни бўлакли - узлуксиз функциялар тўпламида аниқланган дискрет модел билан аппроксимация қилиш мумкин деб ҳисобланади. Бўлакли- узлуксиз функциялар узлуксиз миқдорнинг қаралаётган соҳанинг чекли сондаги нуқталари ёрдамида аниқланади. Умумий ҳолда, узлуксиз миқдорнинг қиймати олдиндан маълум эмас ва бу миқдорни соҳанинг баьзи бир ички қийматларида аниқлаш зарур. Агарда бу миқдорнинг сонли қийматлари соҳанинг ҳар бир ички нуқтасида маьлум деб қабул қилсак, дискрет моделни жуда осон қуриш мумкин. Шундан сўнг биз умумий ҳолатга ўтамиз. Шундай қилиб узлуксиз миқдорнинг дискрет моделини қуриш учун қўйидаги ишларни бажарамиз: 1. Қаралаётган соҳада чекл и сон даги нуқталар белгиланади. Бу нуқталар тугун нуқталар ёки шунчаки тугунлар дейилади . 2. Узлуксиз миқдорнинг ҳ ар бир тугун нуқтада ги қиймат и ўзгарувч и деб ҳисобланади ва аниқланиши зарур . 3. Узлуксиз миқдорни нг аниқлаш соҳаси э лементлар деб аталувчи чекли сондаги қисм соҳаларга бўлинади. Бу э лементлар умумий тугун нуқталарга эга ва биргаликда соҳанинг шаклини аппроксимациялайди . 8 4. Узлуксиз миқдор ҳ ар бир элемент да бу миқдорнинг тугун нуқталардаги қиймати орқали аниқланган кўпҳад орқали аппроксимацияланади. Ҳар бир элемент учун ўзининг кўпҳади аниқланади, лекин бу кўпҳадлар шундай танланадики узлуксиз миқдорни элементнинг чегараси бўйлаб қийматлари узлуксизлигини сақлаши зарур. Чекли элементлар усулининг асосий концепциясини бир ўлчовли ҳолда стерженда берилган температуранинг тақсимланиши 1.1 расмда кўрсатилган. Т ( х ) узлуксиз миқдорни қараймиз , унинг аниқланиш соҳаси - х ўқи бўйлаб йуналган ОL кесмадан иборат .   Х   ўқида бешта нуқта белгиланган ва рақамланган (1.2-расм, а ). Бу тугун нуқталар бир-биридан бир хил масофада бўлиши шарт эмас . 1.1 расм . Бир ўлчовли стерженда температурани тақсимла ни ш и 1.2 расм . Тугун нуқталар ва Т(х) нинг тахминий қийматлари 9 Т ( х ) нинг қийматлари б у ҳолдаҳар бир тугун нуқтада маълум. Бу белгиланган қийматлар 1,2 . б расмда кўрсатилган ва Т 1 ,   Т 2 , ...,   Т 5 . билан белгиланган . Соҳани элементларга ажратиш икки хил йўл билан амалга оширилиши мумкин. Масалан, ҳар бир элементни иккита қўшни нуқта ёрдамида чеклаш ёрдамида тўртта элементни шакллантириш мумкин (шакл 1.3 а) ёки соҳани ҳар бири учтадан тугунни сақлайдиган иккита элементга ажратиш мумкин (1.3.б шакл.). Элементга мос келувчи кўпҳад Т ( х ) тугун нуқталардаги қийматлари орқали аниқланади. INCLUDEPICTURE "../../../../AppData/Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/ FineReader11/media/image5.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/media/ image5.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/media/ image5.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/media/ image5.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/media/ image5.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/ media/image5.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/ media/image5.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../AppData/Администратор/Model/AppData/Roaming/Microsoft/Word/AppData/Local/ Temp/FineReader11/media/image5.png" \* MERGEFORMAT 10 1.5 ш акл. Учбурчак ли ва тўртбурчак ли элементлардан фойдаланиб, икки ўлчовли скаляр функцияни моделлаштириш. INCLUDEPICTURE "../../../../AppData/Model/AppData/Roaming/Microsoft/Word/AppData/ Local/Temp/FineReader11/media/image6.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/ media/image6.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/ media/image6.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/ media/image6.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/ media/image6.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/ media/image6.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../../../Model/AppData/Roaming/Microsoft/Word/AppData/Local/Temp/FineReader11/ media/image6.png" \* MERGEFORMAT INCLUDEPICTURE "../../../../AppData/Администратор/Model/AppData/Roaming/Microsoft/Word/AppData/ Local/Temp/FineReader11/media/image6.png" \* MERGEFORMAT Шакл 1.6. Икки ўлчовли скал я р функцияни квадратик учбурчак ли элемент ёрдамида моделлаштириш. Икки ёки уч ўлчамли соҳада аниқланган узлуксиз миқдорнинг дискрет моделини қуриш учун чекли элементлар усулининг асосий концепцияси худди шундай ишлатилади. Икки ўлчовли ҳолда, элемент функциялари х в а у   ларнинг функцияси орқали ифодаланади ва бунда элементлар кўпроқ учбурчак ёки тўртбурчак шаклида қаралади. Элемент функциялари энди текис (шакл 1.5) ёки эгри чизиқли (шакл 1.6) сиртлар билан тасвирланади. 11 Элемент функцияси эса, агар минимал сондаги тугун нуқталар олинган бўлса, (учбурчак элемент учун учта, туртбурчак элемент учун тўртта ) текисликдан иборат бўлади. Агар ишлатилаётган тугунлар сони минималдан каттароқ бўлса, у ҳолда элемент функциясига эгри чизиқли сирт мос келади. Бундан ташқари, ортиқча тугунлар эгри чизиқли чегарали элементларни қараш имконини беради. Икки ўлчовли узлуксиз φ ( х , у )  м и қ д о р н и н г я к у н и й а п п р о к с и м а ц и я с и ҳар бири φ ( х , у ) нинг мос тугунларидаги қийматлари орқали аниқланган бўлакли - узлуксиз сиртларнинг бирлашмасидан иборат бўлади. Чекли элементлар усулининг муҳим жиҳати элемент функциясини аниқлаш учун элементлар мажмуидан типик элементни ажратиб олиш имконининг мавжудлиги ҳисобланади. Бу элемент функциясини элементнинг соҳада жойлашиш ҳолатига ва бошқа элемент функцияларига боғлиқсиз аниқлаш имконини беради. 1.2. Чекли элементлар усулининг афзалликлари ва камчиликлари Ҳозирги пайтда, чекли элементлар усулининг қўлланиш соҳаси дифференциал тенгламалар билан тавсифланадиган барча физик масалаларни қамраб олган.Чекли элементлар усулининг муҳим афзалликлари қуйидагилардир: 1. Қўшни элементларнинг моддий хусусиятлари албатта бир хил бўлиши шарт эмас. Бу шарт усулни жисм ҳар хил материаллардан ташкил топганда ҳам қўллаш имконини беради. 2. Эгри чизиқли соҳа тўғри чизиқли элементлар ёрдамида аппроксимация қилиниши мумкин ёки уни эгри чизиқли элементлар ёрдамида аниқ қоплаш мумкин бўлади. Шундай қилиб, усулдан 12 чегаралари “яхши” шаклда бўлмаган соҳалар учун ҳам фойдаланиш мумкин 3. Элементларнинг ўлчамлари ўзгарувчан бўлиши мумкин. Бу, агар зарурат бўлса, соҳани ташкил қилган элементларини катталаштириш ёки кичиклаштириш имконини беради. 4.Чекли элементлар усулидан фойдаланиб, сирт юкламаси узилишга эга бўлган чегаравий шартларни шунингдек, аралаш чегаравий шартларни қараш қийин эмас. 5. Юқорида келтирилган чекли элементлар усулининг афзалликларидан маьлум синфдаги хусусий масалаларни ечиш учун етарли даражада умумий дастурларни тайёрлашда фойдаланиш мумкин. Масалан, иссиқлик тарқалишнинг ўққа нисбатан симметрик масаласи учун тузилган дастур ёрдамида шу типдаги исталган хусусий масалани ечиш мумкин. Чекли элементлар усулининг асосий камчилиги ҳисоблаш дастурларини тузиш ва ҳисоблаш техникаларидан фойдаланишнинг зарурлигидир. Мураккаб масалаларни ечиш учун катта хотирага эга бўлган тезкор ЭҲМ лардан фойдаланиш зарур. Ҳозирги вақтда етарли қувватли ЭҲМ ларни яратиш имкониятлари мавжуд. Баъзи тижорат ва бошқарув ташкилотлари кенг кўламли ҳисоблаш дастурларига эга. Ҳисоблаш дастурларини мукаммаллаштириш ва юқори қувватли ЭҲМ ларни яратиш орқали чекли элементлар усулининг асосий камчилигини юмшатиш мумкин. 1.3 Баъзи бир чегаравий масалаларни чекли элементлар усули ёрдамида ечиш. Олдинги иккита мавзуда алоҳида элементда узлуксиз функцияни қандай аппроксимация қилиш кераклиги масаласи кўриб чиқилган. Бундан ташқари, алоҳида элемент учун олинган натижалардан узлуксиз 13 функцияни бутун соҳада аппроксимация қилиш учун зарур бўлган бўлакли-узлуксиз функциялар тўпламини қандай қуриш мумкинлиги кўрсатилди. Бу бўлакли-узлуксиз функциялар тўплами тугунларда аниқланган миқдорларнинг сонли қийматлари орқали топилади. Бизнинг охирги мақсадимиз – тугунларда аниқланган миқдорларнинг шундай сонли қийматларини топишдирки, бу қийматларда элементлар учун ёзилган муносабатлар бирор муҳим физик параметрни жуда аниқ аппроксимацияласин. Чекли элементлар усулининг ривожланишининг дастлабки босқичларида тугун қийматлар физик жараён билан боғлиқ бўлган интеграл миқдорни минималлаштириш орқали аниқланди. Деформацияланувчан қаттиқ жисмлар механикаси масалаларида, масалан, системанинг потенциаль энергияси минималлаштирилади. Натижада, элементни аниқловчи тенгламалар мувозанатнинг алгебраик тенгламалар системасига келтирилади ва бу система тугундаги кўчишларга нисбатан ечилади. Майдон назарияси масалаларида (иссиқлик узатиш, грунт сувлари оқими, магнит майдонларни ҳисоблаш ва бошқ), бирор функционал минималлаштирилади. Бу функционал шундай хоссаларга эга бўладики, уни минималлаштирувчи ихтиёрий функция дастлабки дифференциал тенгламаларни ҳамда чегаравий шартларни қаноатлантириши зарур. Кейинчалик, тугун қийматларини аниқловчи тенгламалар системасини ҳосил қилиш учун вазнли тафовутлар усулларидан фойдаланила бошланди (Масалан, Галёркин усулидан). Ушбу мавзуда чекли элементлар усулининг тенгламаларини ҳосил қилиш бирор интеграл миқдорни минималлаштиришга асосланган ҳолда берилади. Шунинг учун ҳам биз вариацион ҳисобнинг баъзи тушунчалари ҳамда матрицавий муносабатларни дифференциаллаш масалаларига дуч келамиз ва аввало шу масалаларни кўриб чиқамиз. Майдон назарияси масалаларида изланаётган миқдорнинг тугун қийматлари учун тенгламаларни ҳосил қилишни намойиш қиладиган содда мисолни кўриб 14 чиқишдан бошлаймиз. Сўнгра, мана шу мисол учун кўрсатамизки, минималлаштириш жараёни элементлар бўйича интегралларни ҳисоблашгача тугалланиши мумкин. Бу мисол қаралгандан кейин чекли элементлар усулининг тенгламаларини умумий ҳолда келтириб чиқариш, майдон назариясининг уч ўлчовли масалалари учун берилади. Кейинги бўлимда чекли элементлар усулининг тенгламаларини умумий ҳолда келтириб чиқаришни эластиклик назарияси масалаларида қаралади. Майдон назарияси масалалари учун ҳам, эластиклик назарияси масалалари учун ҳам охирги натижалар сирт ва ҳажм интеграллари кўринишда берилади ва бу интеграллар аниқ қўлланиш соҳаси қаралганда ҳисобланади. 1.4 Майдон назаряси масалаларида чекли элементлар усулининг тенгламалари. Олдинги бўлимларда муҳокама қилинган бир ўлчовли иссиқлик тарқалиш масаласи, хусусий ҳосилали дифференциал тенгламалар ёрдамида ифодалаш мумкин бўлган бир неча муҳим физик масалалардан биридир. Бу физик жараёнларнинг ҳар бири учун дифференциал тенглама қўйидаги умумий квазигармоник дифференциал тенгламанинг таркибида жойлашган: ( 1.1 ) бунда ч е гара вий шартлар чегарада ( 1.2 ) ва (ёки) чегарада . (1.3) ва нинг бирлашмаситўлиқ чегарани ҳосил қилади.   ,   ва коэффициентлар, шунингдек миқдор x, y   ва z   нинг 15 функциялари бўлиши мумкин,   лекин дан боғлиқсиз деб фараз қилинади. (1.3) формуладаги   ,     ва   миқдорларсиртга нормал векторнинг йўналтирувчи косинусларидир. (1.1) тенгламани ҳам изотроп ҳам анизотроп жисмларга қўллаш мумкин. Бироқ анизотроп соҳаларда координата ўқлари инерциянинг асосий ўқларига параллел бўлиши керак. Бу (1.1) тенглама чегаравий шартлар билан биргаликда уч ўлчовли соҳада иссиқлик тарқалишини ифодалайди [4]. Бу ҳолда , ва лар иссиқлик ўтказувчанлик коэффициентларига мос келади, Q - ички иссиқлик манбаи, q - сиртнинг бир қисмидаги иссиқлик оқими ва h  - иссиқлик алмашинув коэффициентига мос келади. φ майдон функцияси жисмнинг температурасини белгилайди. Бир ўлчовли ва икки ўлчовли иссиқлик тарқалиш тенгламалари (1.1) формуладан ва (ёки) деб ҳисоблаб, ҳосил қилиниши мумкин. Агарда чегаранинг қисмида φ аниқланмаган бўлса q ва h миқдорларнинг иккаласи ҳам нолга тенг бўлади ва (1.3) шарт қуйидаги шартга келтирилади: ( 1.4 ) Бу шарт иссиқлик ўтказиш йўқлигини ( иссиқлик изоляция ланган чегара) акс эттиради . Икки ўлчовли ҳолда бутун чегара бўйлаб ва бўлган холни кўриб чиқайлик. Бу ҳолда (1.1) тенглама (1.5) тенгламага келтирилади. Бу тенглама кундаланг кесими доира бўлмаган эластик стерженни бураш масалаларида учрайди [5]. майдон функцияси бу ҳолда кучланиш функцияси, –материалнинг эластиклик хусусияти, 16 θ – стержен кесимининг бўралиш бурчаги вазифасини бажаради. Ташқи куч остида пайдо бўладиган силжишнинг кучланиши ни х ва у лар бўйича дифференциаллашдан ҳосил бўлади. Яна бир муҳим икки ўлчовли масала суюқликнинг ўрамасиз оқиши масаласидир, Ушбу мисолда ва (1.1) тенглама (1.6) ва чегаравий шартлар ва (ёки) бўлади. ва лар тупроқнинг ўтказувчанлигини, Q –сув манбаини, майдон функцияси эса пьезометрик напорни билдиради. q  миқдорга чегаранинг сувли қатламли қисми бўйлаб сувнинг сизиб ўтиши мос келади. (1.1) тенглама билан ифодаланадиган бошқа муҳим физик масалалар электростатик ва магнитостатик майдонлар, ҳамда суюқ мойловчи плёнкалар билан боғлиқ. Сўнги масала [3] ишда батафсил ўрганилган. Вариацион нуқтаи назардан (1.2) ва (1.3) чегаравий шартларни қаноатлантирувчи (1.1) тенгламани ечиш (1.7) функционални минимумини топишга эквивалентдир. (1.7) функционални минималлаштириш { Ф } тугун қийматлари тўпламида бажарилиши керак. Шу мақсадда, олдинги бўлимда қаралган процедурвлврдан фойдаланамиз, яъни (1.7) функционални интегралларни ҳисоблашдан олдин минималлаштирамиз. Бу ёндашув, ҳар бир аниқ масала учун элементларнингэнг маъқул характеристикаларини танлаш имконини беради. 17 Минималлаштириш жараёнини (1.7) функционални алмаштиришдан бошлаймиз. Ушбу қадам кейинги операцияларни бироз соддалаштиради. Биз иккита матрицани киритамиз: (1.8) Ва (1.9) у ҳолда (5.32) муносабатни энди қуйидагича ёзиш мумкин: (1.10) функцияни бутунсоҳа бўйлаб узлуксиз эмаслигини эсга олиб, унинг ўрнига ҳар бир алоҳида элементда аниқланган функцияни қараймиз. (5.35) даги интеграллар алоҳида элементлар бўйича олинган интегралларга ажратиш қуйидагини беради: ( 1.11 ) бу ерда Е - элементларнинг умумий сони охирги муносабатни символик равишда ( 1.12 ) кўринишда ёзиш мумкин, бу ерда - алоҳида элементнинг га қўшган ҳиссаси. ни минималлаштириш (1.13) 18 Муносабатнибажарилишини талаб қилади.(1.14) даги хусусий ҳосилаларни (1.12) даги интегралларни тугун қийматлар орқали ифодаланмагунча аниқлаш мумкин эмас.(4.1) муносабатлар (*) (1.11) ни ҳисобга олган ҳолда (5.33) миқдорини ҳисоблаш мумкин ва уни (4.1) билан биргаликда (5.36) га кўйиш мумкин. нинг ифодасини ёзамиз: (1.14) ёки (1.15) бу ерда [ В ] шакл функциясининг ҳосилалари билан боғлиқ маълумотларни сақлайди.Бу миқдорлар ҳозирча номаълум, чунки шакл функциялари ҳали аниқланмаган. (1.1) ва (1.15) формулалардан фойдаланиш, элементлар бўйича олинган (1.12) интегралларни (1.16) шаклда ёзиш имконини беради. Бунда ва миқдорлар маълум коэффициентлардир. Бу миқдорлар интеграл белгиси остида келтирилган, чунки улар элемент ичида ўзгариши мумкин. Агарда 5.2 бўлимдаги дифференциаллаш қоидаларидан фойдаланилса, (1.16) миқдорларни { Ф } бўйича дифференциаллаш мутлоқо оддий амалдир. (1.16) формулани қараймиз: 19 (1.17 ) умумий йиғиндига алоҳида элементнинг ҳиссаси қўйидагига тенг: (1.18) Ушбу интеграллар тўплами ихчам шаклда ёзилиши мумкин: ( 1.19 ) Бу ерда ( 1.20 ) ва ( 1.21 ) 20 Якуний тенгламалар системас и (1.19) ни (1.13) га қўйишдан ҳосил бўлади: ( 1.22 ) ёки ( 1.23 ) бу ерда ( 1.24 ) ва ( 1.25 ) (1.20) даги интеграллар элементнинг иссиқлик ўтказувчанлик матрицасини аниқлайди, (1.21)даги интеграллар эса элементнинг юклама векторини аниқлайди. Бу интеграллар ушбу бўлимдаги тадқиқотларимизнинг асосий натижаларидир. Бу интегралларни ҳисоблаш махсус соҳаларга тадбиқ қилишда муҳокама қилинади. 21 II БОБ . ИССИҚЛИК ЎТКАЗУВЧАНЛИК НАЗАРИЯСИНИНГ АСОСИЙ ТУШУНЧАЛАРИ Кириш Иссиқлик – модданинг ички энергиясининг кинетик қисми бўлиб, бу моддани ташкил этувчи молекулалар ва атомларнинг шиддатли хаотик харакати билан аниқланади. Температура – молекулалар ва атомлар ҳаракати интенсивлигининг ўлчовидир. Маьлум бир температурада иссиқлик миқдори унинг массасига боғлиқ; масалан, бир хил температурада катта стакан сувда кичигидан кўра кўпроқ иссиқлик бор. Иссиқлик инсон ҳаётида, жумладан унинг организмининг фаол ишлашида муҳим рол ўйнайди. Озиқ-овқат таркибида бўлган кимёвий энергиянинг бир қисми иссиқликка айланади ва бунинг натижасида инсон жисмсининг температураи 37 атрофида сақлаб турилади. Инсон жисмидаги температура баланси атроф муҳитга ҳам боғлиқ ва инсонлар қишда ишлаб чиқариш ва яшаш хоналарини иситиш учун ва ёзда совутиш учун кўп энергия сарфлашга мажбур бўлишади. Бу энергиянинг кўп қисмини иссиқлик машиналари, масалан қозон қурилмалари ва ёқилғи қазилмалари (кўмир, нефт)да ишлайдиган ва электр энергияси ишлаб чиқарадиган электростанцияларнинг буғ трубиналари етказиб беради. XXVIII аср охиригача иссиқлик моддий модда ҳисобланиб, жисмнинг температураcи унинг таркибидаги “калорияли суюқлик” ёки “иссиқ жинсли” модда миқдори билан белгиланган. Кейинчалик Б.Рамфорд, Ж.Жоул ва ўша даврнинг бошқа физиклари тажрибалар орқали “калория” назариясини рад этиб, иссиқликнинг вазнсиз эканлигини ва уни шунчаки механик ҳаракат туфайли ҳар қандай миқдорда олиш 22 мумкинлигини исботладилар. Иссиқликнинг ўзи модда ҳисобланмайди – бу фақатгина атом ва молекулалар ҳаракатининг энергиясидир. Замонавий физикада иссиқлик тушунчаси айнан шундай тушунилади. Иссиқлик алмашинуви ёки иссиқлик узатиш – бу жисм ичидаги ёки температуралар фарқига эга бўлган бир жисмдан иккинчи жисмга иссиқликни узатиш жараёнидир. Иссиқликни узатиш моддаларнинг хусусиятларига, температулар фарқига ва табиатнинг экспериментал ўрнатилган қонунларига бўйсунади. Самарали ишлайдиган иссиқлик ёки совутиш тизимларини, ҳар хил двегателларни энергия қурилмаларини иссиқлик изоляция тизимларини яратиш учун иссиқлик узатишнинг талабларини билиш керак. Баьзи холларда иссиқлик алмашинувига эҳтиёж кам (космик кемаларда), баьзи холларда эса эҳтиёж кўп сезилади(Буғ қозонлари, ошхона идишлари). 2.1 Иссиқлик узатишнинг асосий турлари Иссиқлик алмашинувининг учта асосий тури мавжуд: ўтказувчанлик, конвекция ва радиацион иссиқлик узатиш ёки термал нурланиш. Иссиқлик ўтказувчанлик. Агар жисмнинг ичида температура фарқи бўлса, унда иссиқлик энергияси унинг совуқ қисмига қараганда иссиқ қисмидан кўпроқ ўтади. Иссиқлик узатишнинг бундай тури иссиқлик ҳаракати ва молекулалар тўқнашуви туфайли иссиқлик ўтказувчанлиги деб аталади; қаттиқ жисмларда етарлича юқори температурада уни визуал кузатиш мумкин. Шундай қилиб, стерженнинг бир учи газ горелкасида қиздирилганда, иссиқлик энергияси стержен орқали ўтказилади ва қиздирилган учидан маьлум масофада чақнаш тарқалади (ва бу чақнаш қиздириш жойидан узоқлашган сари кам интенсивлик билан амалга ошади). Иссиқлик ўтказувчанлиги туфайли иссиқлик узатишнинг интенсивлиги температура градиентига боғлиқ яьни стержен учларидаги температура фарқининг улар орасидаги масофага нисбати га 23 боғлиқ. Бу нисбат шунингдек, стержен кесимининг юзасига, ва материалнинг иссиқлик ўтказувчанлик коэффицентига боғлиқ, Вт/(м*К). Бу миқдорлар орасидаги муносабат француз математиги Ж.Фурье томонидан киритилган ва қуйидаги кўринишда бўлади Бу ерда Q, q– иссиқлик оқими ва иссиқлик оқимининг зичлиги, Втва –иссиқлик ўтказувчанлик коэффиценти, Вт/(м*К), F– кўндаланг кесим юзаси Бу муносабат Фурьенинг иссиқлик ўтказувчанлик қонуни деб номланади; ”минус” белгиси иссиқликтемпература градиентига қарама- қарши йўналишда узатилишини кўрсатади. Фурье қонунидан келиб чиқадики, иссиқлик оқимини иссиқлик ўтказувчанлик коэффиценти, кесим юзаси ёки температура градиентининг қийматларидан бирини камайтириш орқали пасайтириш мумкин. Қиш шароитида бинолар учун юқоридаги қийматлар амалда ўзгармасдир ва шунинг учун хонада исталган температурани сақлаб туриш учун деворларнинг иссиқлик ўтказувчанлигини пасайтириш, яьни уларнинг иссиқлик изоляциясини яхшилаш керак. Металларнинг иссиқлик ўтказувчанлиги кристалл панжараларнинг тебраниши ва кўп сонли эркин электронларнинг ҳаракати билан боғлиқ. Электронларнинг ҳаракати металларнинг электр ўтказувчанлиги учун ҳам таьсир қилади ва шунинг учун яхши иссиқлик ўтказгичлар (масалан кумуш ёки мис)яхши электр ўтказгичлар ҳам бўлади. 24 Кўпгина моддаларнинг иссиқлик ва электр қаршилиги суюқ гелийнинг температураси (1.8 К )дан паст бўлганда бирданига камайиб кетади. Ўта ўтказувчанлик деб аталувчи бу ҳодисадан микроэлектроника асбобларидан тортиб, электр узатиш ва катта электромагнит линияларигача кўплаб асбобларнинг ишлаш самарадорлигини ошириш учун фойдаланилади. Конвекция. Суюқлик ёки газга иссиқлик юборилганда молекулалар ҳаракатининг интенсивлиги ошади ва натижада босим кўтарилади. Агарда суюқлик ёки газнинг ҳажми чегараланмаган бўлса, улар кенгаяди; суюқликнинг (газнинг) локал зичлиги камаяди ва итарувчи (Архимед ) кучларга асосан муҳитнинг иситилган қисми юқорига ҳаракатланади(айнан шунинг учун ҳам хонадаги иссиқ ҳаво батареядан шифтга қараб кўтарилади). Мана шу ходиса – конвекция деб аталади. Бошқача айтганда иссиқликни маьлум температурага эга бўлган бир соҳадан бошқа температурага эга бўлган соҳага кўчиришдан иборат. Ундаги миқдорлар орасидаги боғланиш Нютон қонунига бўйсунади. Бу ерда Q – иссиқлик оқими, Ватт, – иссиқлик манбаининг сирт юзаси, , – манба ва унинг атрофининг температуралари, К. Конвектив иссиқлик узатишнинг коэффициенти (иссиқлик бериш коэффициенти) муҳитнинг хусусиятларига, унинг молекулаларининг бошланғич тезлигига ҳамда, иссиқлик манбаининг шаклига боғлиқ, . 2.1.1. Иссиқликнинг ўрни ва ундан фойдаланиш 25 Иссиқлик деярли, барча ишлаб чиқариш жараёнларида қатнашади. Улардан энг муҳимлари металларни эритиш ва қайта ишлаш, двигателларнинг ишлаши, озиқ-овқат маҳсулотларини ишлаб чиқариш, кимёвий синтез, нефтни қайта ишлаш, барча турдаги предметлар (ғишт ва идиш товоқлардан тортиб, то автомобил ва электрон қурилмалар)ни ишлаб чиқаришни мисол келтириш мумкин. Кўпгина саноат ва транспорт ишлаб чиқаришлар, ҳамда электростанциялар иссиқликни фойдали ишга алмаштириб берувчи қурилмалар – иссиқлик машиналарисиз ишлай олмайди. Бундай иссиқлик машиналарига компрессорлар, трубиналар, буғ, бензин ва реактив двигателлар мисол бўла олади. Электр энергиясини ишлаб чиқариш ва транспорт орқали кўчириш учун иссиқлик манбаи бўлиб, ядро реакциялари хизмат қилади. 1905 йил А.Эйнштейн масса ва энергия бир-бири билан муносабат билан боғланишини, яьни улар бир-бирига ўтиши мумкинлигини кўрсатди. Бу ерда ёруғлик тезлиги С=300 минг. км/с бўлиб, бу жуда катта миқдордир. Бу формула кўрсатадики жуда кам миқдордаги модданинг миқдори ҳам жуда катта миқдордаги энергияни ҳосил қилиши мумкин. Масалан, 1 кг парчаланувчи миқдордан назарий жиҳатдан қуввати 1 Мвт бўлган электростанция 1000 сутка узлуксиз ишлагандаги энергияни ҳосил қилиш мумкин. 2.2 Ясси деворнинг иссиқлик ўтказувчанлиги 2.2.1 Бир жинсли девор Қалинлиги (1 - расм), иссиқлик ўтказувчанлик коэффиценти , доимий бўлган бир жинсли деворни кўриб чиқайлик. Деворнинг ташқи юзаларида доимий ўзгармас температуралар сақланади. 26 Температура фақат х ўқи бўйлаб ўзгаради. Бу холда температура майдони бир ўлчовли ва изотермик сиртлар текис ва ўқига перпендикуляр жойлашади. х  ўқи бўйлаб девор ичидан иккита изотермик сиртлар билан чегараланган қалинлиги   dx   бўлган қатлам ажратамиз. 1 расм. Ясси бир жинсли девор орқали иссиқлик узатиш. Фурье қонунига асосан, бу ҳолда (2.1) деб ёзиш мумкин. Стационар иссиқлик режимида q иссиқлик оқимининг тезлиги ҳар бир кесимда ўзгармас бўлади. Шунинг учун (2.2) C   интеграллаш ўзгармаси x =0   бўлганда , ва чегаравий шартдан топилади. Бу қийматларни (2.2) тенгламага қўйиб (2.3) ни ҳосил қиламиз. (2.3)дан q иссиқлик оқимининг номаьлум қиймати топилади: 27 (2.4) Натижада бирлик вақт ичида деворнинг бирлик сиртига берилган иссиқлик миқдори λ иссиқлик ўтказувчанлик коэффицентига тўғри пропорционаллиги келиб чиқади. Ҳамда сиртқи сиртларнинг температуралар айирмаси девор қалинлигига тескари пропорционаллиги келиб чиқади. (2.4) тенглама ясси девордан иссиқлик ўтказувчанликнинг ҳисоблаш формуласидир. Бу тенглама тўртта миқдорни ўзаро боғлайди. Улардан ихтиёрий учтасини билган ҳолда, тўртинчисини топиш мумкин. ва (2.5) нисбат деворнинг иссиқлик ўтказувчанлиги дейилади, тескари миқдор эса деворнинг термик қаршилиги дейилади. Термик қаршилик деворда бирлик зичликда иссиқлик оқимининг температураси тушишини аниқлайди. Агарда (2.2) тенгламага С  нинг топилган қийматини ва q, иссиқлик оқимининг зичлигини қийматини келтириб қўйсак, у ҳолда (2.6) температура эгри чизиғининг тенгламасини ҳосил қиламиз. (2.6) тенглама бир жинсли деворнинг температураси иссиқлик ўтказувчанлик коэффиценти ўзгармас бўлганда чизиқли қонуният бўйича ўзгаришини кўрсатади. Ҳақиқатда эса иссиқлик ўтказувчанлик коэффиценти температурага боғлиқ бўлганлиги учун ўзгарувчи миқдор бўлади. Агар бу 28 ҳолатни ҳисобга олсак мураккаброқ ҳисоблаш формулаларини ҳосил қиламиз. Кўпгина материаллар учун иссиқлик ўтказувчанлик коэффицентининг температурага боғлиқлиги кўринишдаги чизиқли характерга эга бўлади. Бу ҳолда Фурье қонунига асосан ясси девор учун (2.7) тенгламани ҳосил қиламиз. Бу ердан ўзгарувчиларни ажратиб ва интеграллашни амалга ошириб (2.8) ни ҳосил қиламиз (2.8) тенгламага ўзгарувчиларнинг чегаравий қийматларини қўйиб х=0  бўлганда t=t 1 (2.9) Ва x= бўлганда t=t 2 (2.10) (2.11) ни ҳосил қиламиз. 29 (2.6) ҳисоблаш формуласи (2.4) формулага қараганда мураккаброқдир. (2.4) формулада иссиқлик ўтказувчанлик коэффицентини ўзгармас ва бирор λ m ўрта қийматга тенг деб қабул қилган эдик. Бу формулаларнинг ўнг томонларини тенглаштириб (2.12) ни ҳосил қиламиз. Демак агар λ m девор температурасининг чегаравий шартларидан ўрта арифметик аниқланганда (2.4) ва (2.6) формулалар тенг қийматли бўлар экан. λ иссиқлик ўтказувчанлик коэффиценти температурага боғлиқлигини ҳисобга олинса, девордаги температура эгри чизиғининг тенгламаси (2.6) тенгламани t  га нисбатан ечиб, С   ўзгармаснинг қийматини қўйишдан ҳосил бўлади: (2.13) Натижада бу ҳолда деворнинг температураси чизиқли эмас балки, эгри чизиқ бўйлаб ўзгаради. Бунда, агар b   коэффицент мусбат бўлса, эгри чизиқнинг қавариқлиги юқорига йўналган, агар b   манфий бўлса, пастга йўналган бўлади. 30 2.3 Ички иссиқлик манбасига эга бўлган жисмнинг иссиқлик ўтказувчанлиги Амалиётда жисм ичидаги иссиқлик ички манбалар ҳисобига хосил бўладиган холлар учраб туради. Масалан электр токи, кимёвий реакциялар, ядровий парчаланиш ва ш.ў. ўтказилса юқоридаги кўрсатилган хол бўлиши мумкин. Бу ҳолларда жисмдан чиқаётган иссиқлик нафақат текис балки, нотекис ҳам бўлиши мумкин. Бундай жараёнлар учун ички иссиқлик манбаларининг қуввати тушунчаси муҳимдир. q v  билан белгиланувчи бу миқдор бирлик ҳажмдан бирлик вақт ичида жисмдан ажралиб чиқувчи иссиқлик миқдорини аниқлайди, Вт/м 3 . Агар жисм иссиқликни ўзига ютса, масалан эндотермик реакциялардагидек, q v   миқдор манфий бўлади ва у иссиқликнинг ҳажм бўйича оқиш интенсивлигини характерлайди. Иссиқликнинг ички манбалари (оқимлари) мавжуд бўлганда жисм ичидаги температура юзаини ҳисоблаш асосий масала ҳисобланади. 2.3.1 Ясси деворнинг иссиқлик ўтказувчанлиги Иссиқлик ўтказувчанлик коэффиценти λ доимий бўлган, қалинлиги 2 δ бўлган бир жинсли ясси деворни кўриб чиқайлик. Бу девор ичида бир текис тақсимланган q v иссиқлик манбалари мавжуд. Чиқарилган иссиқлик деворнинг ён сиртлари орқали атроф-муҳитга ўтади. Деворнинг ўрта қисми юзасига нисбатан иссиқлик ўтказиш жараёни симметрик тарзда бўлади, шунинг учун координаталар бошини кесимга қўйиш ва х ўқини ён томон сиртига пермендикуляр йўналтириш мақсадга мувофиқ. (2 расм) 31 2 расм. Қувурдаги ички иссиқлик манбалари билан иссиқлик ўтказувчанлиги Иссиқлик баланси тенгламасидан келиб чиқадики, ички иссиқлик манбалари мавжуд бўлганда текис девордаги иссиқлик оқимининг зичлиги х нинг ошиши билан чизиқли равишда ўсади ва (2.14) га тенг бўлади. Бу тенгламадан кўриниб турибдики, х =0   да   q  = 0, ва х   = δ да q δ = q v δ ,   яьни максимал қийматга эришади. Фурье қонунига кўра (2.15) Ўзгарувчиларни алмаштириб, қуйидагига эга бўламиз: (2.16) Ушбу тенгламани интеграллаб (2.17) га эга бўламиз. С интеграллаш константаси чегара шартларидан аниқланади. х = 0 да t   = t 0 = С ва температуранинг ўзгариши тенгламаси 32 (2.18) шаклини олади. х  = δ, да t   = t c . Б у ҳолда (2.17) тенгламадан (2.19) келиб чиқади. Бу ерда t 0   - t c   айирма деворнинг ташқи сирти билан ўртаси орасидаги фарқни билдиради. q δ = q λ δ   эса бу чегара сиртларидаги иссиқлик оқими зичлигидир ( х   = δ   бўлганда ). Агар t 0   температура номаьлум бўлса, у ҳолда С   ўзгармасининг қийматини t c   билан ифодаланиши мумкин ва бу ҳолда температура эгри чизиғининг тенгламаси (2.20) шаклини олади. Юқоридаги хулосалар шуни кўрсатадики, бир хил тақсимланган ички иссиқлик манбалари мавжуд бўлганда, текис девордаги температура тақсимоти параболик характерга эга. Ўрта текисликда (x  = 0) да температура энг катта қийматга эга. Катта температура фарқлари бўлганда иссиқлик ўтказувчанлик коэффицентинитемпературага боғлиқлигини ҳисобга олиш керак, . х =0 бўлганда С нинг бу қийматини (2.20)тенгламага қўйиб, температура эгри чизиғининг қуйидаги тенгламасини ҳосил қиламиз (2.21) 33 2.3.2 Доиравий стерженнинг иссиқлик ўтказувчанлиги Иссиқлик ўтказувчанлик коеффиценти λ   ўзгармас бўлган ва радиуси r 0  (8-расм) бўлган чексиз узунликдаги стерженни (цилиндрни) кўриб чиқайлик. Бу стержен ичида тенг тақсимланган q v .   Иссиқлик манбаларининг ташқи юзаси орқали чиқарилган иссиқлик атроф-муҳитга тарқалади. 2 - расм. Ички иссиқлик манбасига эга бўлган стержен нингиссиқлик ў тказувчанлиги Радиуси r ва узунлиги l   бўлган стержен ичидаги ҳар қандай цилиндрсимон элемент учун иссиқлик баланси тенгламаси. (2.22) кўринишга эга бўлади. Бу ердан стерженда ички иссиқлик манбаси мавжуд бўлганда, иссиқлик оқимининг зичлиги q r радиусга пропорционал равишда ўзгаради: (2.23) Бу тенгламадан кўриниб турибдики , яьни ўзининг максимал қийматига эришади. Фурье қонунига кўра 34 (2.24) (2.25) С интеграллаш ўзгармаси чегаравий шартлардан аниқланади. (2.26) ва температура эгри чизиғининг тенгламаси (2.27) кўринишда бўлади. ва тенглама қуйидаги кўринишни олади (2.28) (2.27) тенгламадан (2.28) тенгламани айириб , стерженнинг радиуси бўйлаб температура фарқини ҳосил қиламиз: (2.29) бу ерда . 35 Агар иссиқлик ўтказувчанлик коэффицентининг температурага боғлиқлигини ҳисобга олсак , бу қийматни (2.29) тенгламага қўйиб (2.30) га эга бўламиз. Бу тенгламани интеграллаш орқали (2.31) ни ҳосил қиламиз. C  ўзгармасни қиймати чегаравий шартлардан аниқланади: Ушбу қийматни (2.31) тенгламага қўйиб, t   га нисбатан ечиб, температура чизиғининг қуйидаги тенгламасини оламиз: (2.32) 2.3.3 Цилиндрсимон деворнинг иссиқлик ўтказувчанлиги Ички радиуси r 1   ва ташқи радиуси r 2   бўлган, иссиқлик ўтказувчанлиги λ доимий б ў лган чексиз узун цилиндрсимон деворни (қувурни) к ў риб чиқайлик. Бу девор ичида бир хил тақсимланган иссиқлик манбалари кв. Деворда чиқарилган иссиқлик атроф-муҳитга фақат ташқи ёки фақат ички юза орқали ёки бир вақтнинг ў зида қувурнинг ик к ала юзаси орқали олиб ташланиши мумкин. 36 а) Иссиқлик қувурнинг ташқи юзаси орқали чиқарилади. Девор қалинлигида изотермик юзалар билан чегараланган r 1 ва r 2   радиусли ҳалқасимон қатламни ажратамиз (3-расм). 3 расм – Ички иссиқлик манбалари билан цилиндрсимон деворнинг иссиқлик ўтказувчанлиги Фурье қонунига кўра, иссиқлик оқими бирлик узунликдаги r радиусли сирт орқали узатилади. (2.33) Кўриб чиқилаётган холатда , ушбу қийматни тенгламага алмаштириб , ўзгартиришни амалга оширамиз . (2.34) Интегр аллаш тенгламаси (2.34) дан қуйидагини: (2.35) Интеграл константаси C чегара шартларидан аниқланади. r =0   учун C  қийматни алмаштириб, биз температура эгри чизиғининг тенгламасини оламиз. 37 (2.36) Қиймати бўлган нишаб, девордаги температуранинг пасайишини оламиз (2.37) Агар иссиқлик ўтказувчанлик коэффицентининг температурага боғлиқлигини ҳисобга олсак, температура эгри чизиғи қуйидаги кўринишга эга бўлади: (2.38) б) Иссиқлик қувурнинг ички юзаси орқали чиқарилади. Жараён диаграммаси 3 расмда кўрсатилган. Бу ерда ҳисоблаш формулаларини чиқариш аввалги ҳолатда бўлгани каби айнан бир хил. Шунинг учун, температура юзаси учун якуний тенгламалар ва бу ердаги температура фарқи ҳеч қандай тарзда фарқ қилмайди, фақат уларда 1 ва 2 индекслари ҳамма жойда тескари томонга ўзгаради (яьни, 2 ва 1 га). Амалий ҳисоблар учун қулай шаклдаги ушбу тенгламалар қуйидаги шаклга эга: температура эгри чизи ғ и тенгламаси : 38 (2.39) Девордаги температура фарқи: (2.40) (2.41) Агар иссиқлик ў тказувчанлик ко э ффи ц иентининг температурага бо ғ лиқлигини ҳисобга олсак, температура эгри чизи ғ и қуйидаги к ў ринишга эга б ў лади. (2.42) c ) Иссиқлик қувурнинг ик к ала юзаси орқали чиқарилади. Биринчи ҳолатда (а) трубанинг ички юзаси энг юқори температурага эга, иккинчисида (б) у ташқи, учинчисида ( c ) бундай сирт девор ичида бир жойда жойлашган; у учун q  = 0. 39 4 расм. – Иссиқлик қувурнинг иккала юзаси орқали чиқарилади Фараз қилайлик, бу сиртнинг радиуси , температура с и эса (4-расм). Кейин, тенгламалардан фойдаланиб (2.43) ни ҳосил қиламиз. , (2.44) Ушбу тенгламаларнинг чап ва ўнг томонларини айириб, қуйидагини ҳосил қиламиз (2.45) (2.45) тенгламадан ни келтириб чиқарамиз. (2.46) 40 Топилган қийматини (2.44) ва (2.45) тенгламаларга алмаштириб, қийматини аниқлаймиз. Агар t 1 = t 2    бўлса, (2.46) тенглама соддалаштирилади ва қуйидаги кўринишга эга бўлади: (2.47) Иккинчиси шуни англатадики, бу ҳолда r 0    иссиқлик шароитларига боғлиқ эмас ва фақат қувур ўлчамлари билан белгиланади. ( масалан , r 2 = 2 и r 1 = 1 r 0 = 1,46). 2.4 Конвектив иссиқлик алмашиш 2.4.1 Умумий тушунчалар ва таьрифлар Иссиқликнинг, қ аттиқ жисмнинг ва суюқ лик муҳит ининг сиртлари орқали ўтказиш жараёни к онвектив иссиқлик алмашиниш ёки иссиқлик бериш деб аталади. Бундай ҳолда, иссиқлик узатиш иссиқлик ў тказувчанлиги ва конвекциянинг бир вақт да бажарилиши таь сири билан амалга оширилади. Суюқлик ва газларда, ҳамда, қаттиқ жисмларда иссиқлик ўтказувчанлик ҳодисаси иссиқлик ўтказувчанлик коэффициенти ва температура градиенти орқали тўлиқаниқланади. Конвекция ҳодисасида эса сал бошқачароқ бўлади. Бу ерда иссиқликни узатиш муҳитнинг ўзини узатиш билан биргаликда кечади. Шунинг учун конвекция заррачалари осон қўзғалганлиги учун фақат суюқликлар ва газларда мумкин бўлади . Пайдо бўлиш хусусиятига кўра ҳаракатнинг икки тури ажратилади: эркин ва мажбурий. Ҳаракат агарда у иситилган ва совуқ суюқлик заррачаларининг тортишиш юзаидаги қиздирилган ва совуқ 41 суюқлик заррачаларининг зичликларининг фарқи натижасида юзага келадиган ҳаракат эркин дейилади. Эркин ҳаракатнинг пайдо бўлиши ва интенсивлиги жараённинг иссиқлик шароитлари билан белгиланади ва суюқлик турига, температура фарқига, тортишиш майдонининг кучига ва жараён содир бўлган фазонинг ҳажмига боғлиқ бўлади. Эркин ҳаракатта табиий конвекция деб ҳам аталади. Ташқи қўзғатувчилар таьсирида содир бўладиган мажбурий ҳаракат деб аталади, масалан, вентиляторнинг насоси ва бошқалар. Умумий ҳолда, мажбурий ҳаракат билан бирга, эркин ҳаракат ҳам бирвақтнинг ўзида ривожланиши мумкин. Эркин ҳаракатнинг нисбий таьсири суюқликнинг алоҳида нуқталар орасидаги температура айирмаси қанчалик катта бўлса, шунча катта бўлади ва мажбурий ҳаракатнинг тезлиги қанча кичик бўлса шунчалик кам бўлади. Конвектив иссиқлик алмашинувининг интенсивлиги иссиқлик бериш коеффитсиенти билан характерланади ва у Нютон- Рихманформуласи (2.48) билан аниқланади. Ушбу қонунга кўра, иссиқлик оқими Q  иссиқлик алмашинувчи F   сиртга ва девор ва суюқликнинг температуралари фарқи (t   с   - t ж ) пропорционалдир. Иссиқлик алмашиниш коэффициенти бирлик вақт ичида бирлик юза томонидан сирт ва суюқлик температураларидаги фарқдаги берилаётган иссиқлик миқдори сифатида аниқланиши мумкин: (2.49) 42 Умумий ҳолда, иссиқлик узатиш коэффициенти иссиқлик узатиш юзаси бўйлаб ўзгариши мумкин ва шунинг учун сирт устида ўртача ҳисобланган. Иссиқлик узатиш жараёнлари суюқлик ҳаракатининг шартлари билан узвий боғлиқдир. Маьлумки, иккита асосий оқим режими мавжуд: ламинар ва турбулент. Ламинар режимда оқим тинч, реактив характерга эга. Ҳаракат режимининг ўзгариши маьлум бир вақтда содир бўлади. Ҳар бир алоҳида ҳолатда ҳар хил бўлган "критик" тезлик. О.Рейнольдс 1883 йилда маxсус тадқиқотлар натижасида суюқликнинг оқиш режими умумий ҳолда фақат битта тезлик билан эмас, балки суюқлик ҳаракатитезлиги w, суюқликнинг қовушқоқликнинг кинематик коэффиценти v ва суюқликоқувчи каналнинг l  ўлчамига боғлиқ бўлган маxсус ўлчамсиз wl/v   комплексига боғлиқ эканлигини аниқлади. Хозирда бундай комплекс Райнольдс сони деб аталади ва R е =   wl / v   билан белгиланади. Ламинар режимдан турбулент режимга ў тиш бу соннинг R е кр сонининг критик қийматида содир б ў лади. Масалан, суюқлик қувурларда ҳаракат қилганда, R е кр =   w кр d / v = 2*10 3 тенг бўлади. 5 - расм Суюқлик оқимининг режимлари Турбулент ҳаракатда бутун оқим тартибсиз ҳаракатланувчи бурамалар билан тўла бўлади ва улар доимий равишда пайдо б ў лади ёки 43 йўқ б ў либ кетади. Бурамалар ҳосил бўлиш механизми ҳали аниқ ўрнатилмаган . Уларнинг пайдо б ў лишининг сабабларидан бири ламинар оқимнинг турғунлиги ни йў қоли ши , кейинчалик ядрога тарқаладиган ва ривожланиб, бутун оқимни т ў лдирадиган гирдобларнинг шаклланиши билан бирга келади. Шу билан бирга, суюқликнинг қовуш қоқлиги туфайли бу гирдоблар аста-секин парчаланади ва йў қолади. Гирдоблар нинг узлуксиз шаклланиши ва уларнинг тарқалиши туфайли суюқликнинг кучли аралашуви содир б ў лади, бу турбулент аралаштириш деб аталади. Қанчалик к ў п гирдоб лар б ў лса, суюқликнинг аралашиши шунчалик интенсив бўлади ва турбулентлик кучаяди. Икки хил турбулентлик фарқланади: т абиий ва сун ь ий. Биринчиси табиий равишда ў рнатилади. Силлиқ қувур ичида барқарор ҳаракатланиш ҳолатида турбулентлик т ў лиқ Re   сон ининг қиймати билан аниқланади. Иккинчиси оқимда ҳар қандай т ў сиқлар, турбулент панжаралар ва бошқа безовта қилувчи манбаларнинг мавжудлиги сабабли суньий равишда юзага келади. Лекин турбулентликнинг исталган турида ҳам сиртнинг юпқа қатламида суюқликнинг қовушқоқлиги сабабли суюқлик оқими секинлашади ва суюқлик нолга тушади. Бу қатлам қовушқоқ қатлам ости деб аталади. Иссиқлик узатиш жараёнлари учун ишчи суюқликнинг ҳаракатланиш режими катта аҳамиятга эга, чунки бу билан иссиқлик узатиш механизми аниқланади. Ламинар режимда деворнинг нормали йўналишида иссиқлик узатиш асосан иссиқлик ўтказувчанлиги йўли билан амалга оширилади. Турбулент режимда бундай иссиқлик ўтказиш фақат қовушқоқ қатлам остида сақланади ва турбулент ядро ичида иссиқлик узатиш суюқлик зарраларининг интенсив аралашиши орқали амалга оширилади. Бу шароитларда газлар учун ва оддий суюқликлар учун иссиқлик узатиш интенсивлиги асосан деворга яқин қатлам остининг термик қаршилиги билан аниқланади ва у ядронинг термик қаршилигига ҳал қилувчи таьсир қилади. Бунга суюқлик температурасининг девор 44 нормали йўналишида суюқлик температурасининг ўзгаришини кузатиш орқали ишонч ҳосил қилиш мумкин. Кўриниб турибдики, температуранинг энг катта ўзгариши сирт яқинидаги нозик бир қатлам ичида содир бўлади, бу орқали иссиқлик ўтказувчанлик орқали берилади. Шунинг учун оқимнинг ламинар режимида ҳам, турбулент режимида ҳам сиртга атрофида турбулент оқим Фурье қонуни қўлланилади. 2.4 Иссиқлик алмашинувининг дифференциал тенгламалари Бирор ҳодисани ўрганиш бу ҳодисани тавсифловчи миқдорлар ўртасидаги муносабатни ўрнатишни англатади. Бу миқдорлар вақт ва маконда ўзгариб турувчи мураккаб ҳодисаларда ўзгарувчилар орасидаги боғлиқликни аниқлаш жуда қийин. Бундай ҳолларда, кам вақт оралиғи ва фазони кам қисмини эгаллайдиган ўзгарувчилар (координаталар, вақт ва физик хусусиятлар)орасидаги боғлиқлик билан чегараланиш етарли. Шу тарзда олинган боғлиқлик кўриб чиқилаётган жараённинг умумий дифференциал тенгламаси бўлади. Ушбу тенгламани интеграллаш орқали бутун соҳа учун ва қаралаётган вақт оралиғи учун миқдорлар орасидаги аналитик боғлиқликни ҳосил қиламиз. Бундай дифференциал тенгламалар ҳар қандай жараён ва хусусан, иссиқлик узатиш жараёни учун ҳам тузилиши мумкин. Иссиқлик алмашинуви нафақат иссиқлик, балки гидродинамик ҳодисалар билан ҳам аниқланганлиги сабабли, бу ҳодисалар мажмуи дифференциал тенгламалар системаси билан аниқланади ва бу системага иссиқлик ўтказувчанлик тенгламалари, ҳаракат тенгламалари ва узлуксизлик тенгламаси киради. Иссиқлик ўтказувчан тенгламаси энергиянинг сақланиш қонуни асосида чиқарилади. 45 Ҳаракатланувчи суюқлик оқимида юзлари dx, dy   ва dz   бўлган элементар параллелепипедни ажратиб кўрсатамиз ва λ , с р ва ρ физик параметрларини доимий деб фараз қилиб, унинг иссиқлик баланси тенгламасини ёзамиз. Агар босимнинг ўзгариши эьтиборга олинмаса, у ҳолда термодинамиканинг биринчи қонунига кўра, берилган иссиқлик миқдори жисмнинг энталпиясининг ўзгаришига тенг бўлади. 6 –расм. Иссиқлик ўтказувчанлигининг дифференциал тенгламаси Иссиқлик ўтказувчанлиги туфайли элементнинг юзлари орқали иссиқлик оқимини ҳисоблайлик. Фурье қонунига кўра, ABCD юзиорқали x   ўқи йўналиши бўйича d τ   вақтичида ўтадиган иссиқлик миқдори. dx,  dy,  dz,  dT  га   қисқартирилгандан сўнг ва ўнг ва чап томонга ўтказинг. С р ρ   тенглама қуйидаги шаклни олади (2.50) Бу иссиқлик ўтказувчанлик учун Фурье-Кирхҳофф дифференциал тенгламаси. Ҳаракатланувчи муҳитнинг исталган нуқтасида вақтинчалик ва фазовий температура ўзгаришлари ўртасидаги алоқани 46 ўрнатади; бу ерда a  температуранинг чаққонлик коэффициенти ва Δ 2 – Лаплас оператори. Ушбу қийматни (50) тенгламага алмаштиргандан сўнг биз қуйидагиларга эга бўламиз: (2.51) Ҳаракатланувчи суюқликларда иссиқлик ўтказувчанлиги жараёнини ўрганишда тенглама қўлланилади. Қаттиқ жисмларда қўлланилганда (2.51) тенглама қуйидаги шаклни олади. (2.52) Юқоридаги тенгламаларни бир-бирига тенглаштириб ва dv   томонидан бекор қилиб, қуйидагини ҳосил қиламиз: (2.53) Ушбу тенгламанинг барча аьзолари ҳажм бирлиги (Н/м 3 ) куч ўлчамига эга. Қисқартириш ва барча шартларни ушбу тенгликнинг чап томонига ўтказгандан сўнг қуйидагига эришамиз: (2.54) Ушбу тенгламаларнинг ўнг томонларини тенглаштириб 47 (2.55) ни ҳосил қиламиз. Суюқликдаги маьлум температура юзасидан иссиқлик узатиш коэффициентини аниқлаш имконини берадиган бу тенглама иссиқлик узатиш тенгламаси деб аталади. 2.6.1 Суюқлик ва газлардаги иссиқлик алмашинуви Ясси сирт (пластинка) атрофида оқаётганда иссиқлик узатиш Жараённинг ривожланиши учун гидродинамик шароитлар Суюқликнинг текис сирт бўйлаб оқими билан динамик чегара қатлами ҳосил бўлади, унинг ичида ёпишқоқ ишқаланиш кучлари туфайли тезлик қатламнинг ташқи чегарасидаги бузилмаган оқим тезлиги w 0  қийматидан нолга ўзгаради. Пластинка юзасининг ўзи. Оқим сирт бўйлаб ҳаракатланаётганда, чегара қатламининг қалинлиги аста-секин ўсиб боради; 7 расм. – Гидродинамик жараённинг ривожланиш шартлари Деворнинг секинлаштирувчи тасири суюқликнинг тобора узоқроқ қатламларига тарқалади. Плитанинг олдинги четидан қисқа масофаларда чегара қатлами жуда нозик ва ундаги суюқлик оқими ламинар характерга эундан ташқари, х кр ма m л лаб масофада чегара қатламида гирдоблар пайдо бўла бошлайди ва оқим турбулент бўлади. Гирдоблар суюқликнинг 48 чегара қатламида интенсив аралашишини та ь минлайди, аммо сиртга яқин жойда улар парчаланади ва бу е рда жуда нозик ёпишқоқ пастки қатлам сақланиб қолади. Жараённинг ривожланишининг тасвири 7 - расмда кўрсатилган. Чегара қатламининг қалинлиги ᵟ   пластинканинг олдинги четидан масофага, оқим тезлиги w 0   ва кинематик ёпишқоқлик ко э ффи ц иентига бо ғ лиқ. Ламинар чегара қатлами билан (2.56) Турбулент чегара қатлами билан (2.57) Бу ерда Re x = w o xlv - Рейнольдс сони, бунда характеристик ўлчам сифатида x  масофа олинади. Чегара қатламидаги суюқлик оқимининг турбулент режимига ўтиш Рейнольдс сонининг критик қиймати билан белгиланади. (2.58) Пластинка атрофида оқим бўлса, одатда 5·10 5 га тенг бўлади. 2.7 Радиацион иссиқлик узатиш Радиация барча жисмларга хосдир, энергиянинг нурланиши эса, интенсивлиги жисмнинг температураси билан белгиланадиган мураккаб атом ичидаги бузилишлар натижасида узлуксиз содир бўлади. Нурланиш энергияси – жисмдан чиқадиган ва вакуумда ёруғлик тезлигида с=3 ·10 8 тарқаладиган турли тўлқин узунликдаги электромагнит тебранишлар энергияси. Одатда, 0,4 дан 40 микронгача 49 бўлган тўлқин узунликларига тўғри келадиган термал нурланиш деб аталади. Бундай нурлар бошқа жисмлар томонидан ютилиши мумкин ва улар ютилганда нурланиш энергияси яна иссиқликка айланади. Электромагнит тўлқинларнинг қўзғатувчиси зарядланган моддий зарралар, яьни модданинг бир қисми бўлган электронлар ва ионлардир. Бундай ҳолда, ион тебранишлари паст частотали нурланишга мос келади; электронлар ҳаракатидан келиб чиқадиган нурланиш, агар улар атомлар ва молекулаларнинг бир қисми бўлса ва уларнинг мувозанати яқинида муҳим кучлар томонидан ушлаб турилган бўлса, юқори частотага эга бўлиши мумкин. Радиацион энергия жисмга тушганда, бу энергиянинг фақат бир қисми сўрилади; унинг яна бир қисми акс этади, бир қисми эса жисмдан ўтади. Уларга тушган барча нурланиш энергиясини ўзлаштирадиган жисмлар мутлақ қора деб аталади. Уларга тушаётган нурланиш энергиясини тўлиқ акс эттирувчи жисмлар абсолют оқ, устига тушган барча энергияни ўтказиб юборадиган жисмлар эса абсолют шаффоф деб аталади. Табиатда мутлақо қора, оқ ва шаффоф жисмлар мавжуд эмас. Амалда шаффоф жисмлар бир ва икки атомли газлар - ҳаво, азот, кислород, водород ва бошқалардир. Қаттиқ ва суюқликлар иссиқлик нурлари учун шаффоф эмас. Қаттиқ жисмлар томонидан нурланиш энергиясининг ютилиши ва акс этиши кўп жиҳатдан уларнинг сиртининг ҳолатига боғлиқ: силлиқ ва силлиқланган юзалар юқори даражада акс этади; Қўпол юзалар, аксинча, юқори ассимилятсия қилиш қобилиятига эга. Унга тушадиган нурланиш энергиясининг 90 - 96% ни ўзлаштирадиган соот, мутлақо қора жисмга яқин бўлган энгюқори сингдириш қобилиятига эга. Металлларда кўп электронлар эркиндир. Шунинг учун, бу ҳолда мувозанат марказлари яқинидаги тебранишлар ҳақида гапириш мумкин 50 эмас.Электронлар ҳаракатланади ва шу билан бирга тартибсиз тормозланишни бошдан кечиради. Натижада, металларнинг нурланиши импулс характерини олади ва турли частотали тўлқинларга, шу жумладан паст частотали тўлқинларга эга. Тўлқин хусусиятларидан ташқари, нурланиш корпускуляр хусусиятларга ҳам эга. Корпускуляр хусусиятлар шундани боратки, нурланиш энергияси доимий равишда эмас, балки алоҳида дискрет қисмларда – ёруғлик квантлари ёки фотонларда чиқарилади ва сўрилади. Эмиссия қилинган фотон - бу энергия, импульс ва электромагнит массага эга бўлган материя зарраси. Фотонларнинг моддадан ўтиши – бу модданинг атомлари ва молекулалари томонидан фотон энергиясини сингдириш ва кейинчалик чиқариш жараёни. Шундай қилиб, нурланиш икки томонлама хусусиятга эга, чунки у электромагнит тўлқинлар майдонининг узлуксизлиги ва фотонларга хос бўлган дискрет хусусиятларга эга. Иккала хусусиятнинг синтези тасвирдир, унга кўра энергия ва импулс фотонларда тўпланган ва уларни космосда у ёки бу жойда топиш эҳтимоли тўлқинларда. Шунга кўра, нурланиш тўлқин узунлиги ( λ ) ёки тебраниш частотаси ( υ =с/ λ ) билан тавсифланади. Электромагнит нурланишнинг барча турлари бир хил табиатга эга ва фақат тўлқин узунлигида фарқланади. Кўпгина қаттиқ ва суюқ жисмлар доимий эмиссия спектрига эга, яьни улар 0 дан ∞ гача бўлган барча тўлқин узунликларининг энергиясини чиқарадилар. Узлуксиз нурланиш спектрига эга бўлган қаттиқ жисмларга электртокини ўтказмайдиган ва ўтказгичлар, шунингдек, оксидланган ҳолатда бўлган турли металлар киради. Баьзи жисмлар энергияни фақат маьлум тўлқин узунликлари оралиғида чиқаради, яьни улар узлуксиз спектр билан энергия чиқаради. Буларга соф металлар ва газлар киради. Турли жисмларнинг нурланиши ҳар хил. Бу жисмнинг табиатига, 51 температурага, сирт ҳолатига ва газлар учун, шунингдек, қатлам қалинлиги ва босимига боғлиқ. Табиатда ва технологияда учраган қаттиқ ва суюқ жисмларнинг аксарияти сезиларли ютувчи ва эмиссия қобилиятига эга. Натижада, нурли иссиқлик узатиш жараёнларида фақат нозик сирт қатламлари иштирок этади. Газсимон жисмлар қаттиқ ва суюқ жисмларга қараганда анча паст нурланишга эга. Шунинг учун унинг барча зарралари газларнинг нурланишида иштирок этади ва термал нурланиш жараёни ҳажмли хусусиятга эга. Барча жисмларнинг нурланиши температурага боғлиқ. Ҳароратнинг ошиши билан радиация кучаяди, чунки жисмнинг ички энергияси ортади. Жисм температурасининг ўзгариши нафақат нурланиш интенсивлигининг мутлақ қийматининг ўзгаришига олиб келади, балки нурланишнинг спектрал таркиби ёки "ранги" нинг ўзгариши билан бирга келади. Ҳароратнинг ошиши билан қисқа тўлқинли нурланишнинг интенсивлиги ошади ва спектрнинг узун тўлқинли қисмининг интенсивлиги пасаяди. Радиациянинг температурага боғлиқлиги иссиқлик ўтказувчанлиги ва конвекция жараёнларига қараганда анча катта. Шунинг учун паст ҳароратларда конвецсия ва иссиқлик ўтказувчанлиги туфайли иссиқлик узатиш устун рол ўйнаши мумкин ва юқори ҳароратларда иссиқлик нурланиши иссиқлик узатишнинг асосий тури бўлиши мумкин. 2.8.2 Иссиқлик нурланишининг қонунлари Планк қонуни. Электромагнит тўлқинларнинг умумий табиатига кўра, нурланиш бўйсунадиган асосий қонунлар улар учун умумийдир. Бу қонунлар мутлақ қора жисм бўлган идеал жисмга ва термодинамик мувозанатли нурланишга нисбатан олинади. Мувозанатли нурланиш билан, маьлум бир ёпиқ нурланиш тизимига киритилган барча жисмлар бир хил температурани олади. 52 Планк қонуни нурланишнинг асосий қонунларидан биридир. Бу радиация интенсивлигининг ҳарорат ва тўлқин узунлигига боғлиқлигини аниқлайди, Вт/м 2 (2.72) Бу ерда с 1 = 0,321·10 -15 ккал∙м 2 /ч = 0,374 ·10 -15 вт∙м 2   биринчи Планк доимийси с 2 = 1,4388 ·10 -2 м · ° К   иккинчи Планк доимийси; λ – тўлқин узунлиги, м; Т – мутлақ ҳарорат, °К . Тенгламага кўра, ҳар бир тўлқин узунлиги нурланиш интенсивлигининг ўзига хос қийматига эга. Планк қонуни идеал жисм учун олинганлиги сабабли, ҳақиқий жисмлар учун у максимал мумкин бўлган нурланиш интенсивлигини ифодалайди. Стефан-Болтзман қонуни. Стефан-Болцман қонуни интеграл ярим шарсимон нурланиш зичлигининг ҳароратга боғлиқлигини белгилайди. Бу қонунга кўра, вақт бирлигида тарқаладиган Q иссиқлик миқдори нурланувчи жисмнинг юзаси F   ва унинг абсолют ҳарорати Т нинг тўртинчи даражасига пропорсионалдир. Техник ҳисоблар учун бу қонунни қуйидаги кўринишда ёзиш мумкин. (2.73) Бу ерда C – мутаносиблик коэффициенти, нурланиш коэффициенти деб аталади. Агар QW   да, Ф еса м 2 да ифодаланган бўлса, у ҳолда э миссивликнинг ўлчами (2.75) 53 Эмиссия коэффициенти бутунлай қора жисм учун енг юқори қийматга ега C с = 5,68 Вт/м 2 · К 4 Бошқа жисмлар учун эмиссияни бутунлай қора жисмнинг эмиссияси билан ифодалаш мумкин, Вт/м 2 · К 4 С  = ε С с =5,68 ε (2.76) бу ерда жисмнинг нурланиш даражаси деб аталадиган енинг қиймати берилган жисмнинг нурланиш кучининг бутунлай қора жисмнинг нурланиш кучига нисбати. Кирҳгофф қонуни. Кирхгоф қонуни жисмнинг нурланиш қобилияти ўртасидаги муносабатни ўрнатади. Бу қонунга кўра қоралик даражаси бир- бирига тенг ε = А ,(2.77) Бу ерда А – жисм томонидан сўрилган нурланиш энергиясининг унинг танага тушган умумий миқдорига нисбати. Кирхгоф қонунидан келиб чиқадики, жисмнинг нурланиш қобилияти қанчалик юқори бўлса, унинг ютиш қобилияти шунчалик юқори бўлади. Бу бутунлай қоратананинг энг юқори эмиссиясини тушунтиради, чунки у учун А = 1, ва шунинг учун ε = 1. III-БОБ. ИССИ КЛИК Ў ТКАЗУВЧАНЛИК ВА КОНВЕКЦИЯ ХИСОБИДАН ИССИКЛИК КУЧИШИ ЖАРАЁНИНИНГ БАЬЗИ МАТЕМАТИК МОДЕЛЛАРИНИ ТАДКИК ЭТИШ . Кўпгина муҳандислик муаммоларида муҳим жиҳат жисмдаги температура тақсимотини билишдир. Агар температура тақсимоти маьлум бўлса, жисмга бериладиган ёки йўқотадиган иссиқлик миқдорини ҳисоблаш мумкин. Бундан ташқари температура юзаси кучланиш тақсимотига таьсир қилади. Агар жисмда температура кучланиши мавжуд 54 бўлиб, у барча йўналишларда эркин тарқала олмаса, у холда ҳар бир жисмда температура кучланишлари вужудга келади. Бундай кучланишларни айланувчи механизмлар (реактив двигателлар ёки буғ генераторлари)ни лойиҳалашда ҳисобга олиш зарур. Температура кучланишларини ҳисоблаш учун биринчи навбатда жисмдаги температуранинг тақсимотини аниқлаш керак . Ушбу бобда жисмдаги температура тақсимотини аниқлаш учун чекли элементлар усулини қўллаш муҳокама қилинади. 3.1 Иссиқлик узатиш тенгламалари Узлуксиз муҳитда  иссиқлик  ўтказувчанлиги  тенгламаси (3.1) кўринишда бўлади. Бу ерда Т - температура; - х,  y  ва z йўналишларидаги иссиқлик ўтказувчанлик коэффициентлари, ўлчамлар кВт  / м  * К;   Q – жисм ичидаги иссиқлик манбаи бўлиб, агар жисмга иссиқлик берилса, унинг ишораси мусбат деб ҳисобланади. Унинг ўлчамларик Вт/м 3 (3.1) тенглама икки хил турдаги чегаравий шартларни бирлаштиради. Агар чегаранинг бирор қисмида температура маьлум бўлса, унда (3.2) кўринишда ёзилади. Бу ерда – чегарадаги температура бўлиб, сиртнинг нуқталарини координаталарининг функцияси бўлиши мумкин. Агар чегарада конвектив иссиқлик алмашинуви содир бўлса, у миқдор билан характерланади, ёки иссиқлик оқими берилган бўлса, у холда чегаравий шарт. (3.3) 55 кўринишда бўлади. Бу ерда - иссиқлик алмашиниш коеффиценти, кВт/м 2 * К ; Т – чегарадаги температура (номаьлум), К ; - атроф-муҳит температураси (маьлум), К ; - йўналтирувчи косинуслари; - иссиқлик оқими, кВт/м 2 (агар иссиқлик жисмдан йўқотилаётган бўлса, мусбат ҳисобланади). Иссиқлик оқими ва конвектив иссиқлик йўқотилиши чегаравий сиртнинг бирор қисмида бир хил вақтда мавжуд бўлолмайди. Агар конвекция туфайли иссиқлик йўқотишлари бўлса, у ҳолда иссиқлик оқими ҳисобига иссиқликнинг чиқиши ёки кириши йўқ ва аксинча. (3.1) ва (3.3) тенгламаларни бир ўлчовли ва икки ўлчовли масалаларга кераксиз координаталар билан боғлиқ ҳадлар ўчирилгандан сўнг қўлланилиши мумкин. Бир ўлчовли масала учун тенглама қуйидагича ёзилади: (3.4) Чегаравий шарти (3.5) бўлади. Агар конвектив иссиқлик алмашинуви бўлмаса, ва бундан ташқари иссиқлик оқими нолга тенг бўлса, (3.3) тенглама муносабатга келтирилади ва бу муносабат иссиқлик сақлайдиган чегаранинг мавжудлиги шартини ифодалайди. (3.1) билан боғлиқ функционални минималлаштириш 1 – бобда мухокама қилинган эди. Иссиқлик узатишнин бир ўлчовли ҳолатини кўриб чиқишни бошлашдан олдин ушбу муҳокама натижаларини шу ерда умумлаштириш 56 мақсадга мувофиқдир. Элементнинг иссиқлик ўтказувчанлик матрицасини ёзамиз: (3.6) матрицаси шакл функцияларини ўзида сақлайди ва (3.7) иссиқлик ўтказувчанлик коэффициентларининг қийматларини ўзида сақлайди: (3.8) матри ц ани х,  y   ва z   га нисбатан дифферен ц иалла ш орқали олинади. ни аниқловчи муносабат (3.9) кўринишга эга бўлади. Алоҳида э лемент у ч ун тенгламаларнинг ў нг томонидаги устун вектор ( 1.21 ) формула билан аниқланади: 57 (3.10) бу ерда Q ,  q   ва h   миқдорлар берилган сонли қийматларга эга. Ю қоридаги формулалар иссиқлик ў тказув ч анлиги туфайли иссиқлик узати ш масаласи да э лементларнинг матри ц аларини тузи ш у ч ун зарур б ў лган бар ч а ма ь лумотларни ў з и ч ига олади. Кейинги бир не ч та б ў лимларда бизнинг эь тиборимиз бита э лемент у ч ун тенгламаларга қаратилади, ш унинг у ч ун биз э лемент матри ц аларининг бар ч а ё зувларида ю қори индекс ( e ) ни тушириб қолдирамиз , икки хил э лементни фарқла ш зарурати бундан мустасно. 3.1. Иссиқлик узати ш учун бир ў л ч овли ҳол Бир ўлчовли чизиқли элемент учун интерполяция кўпҳади (3.11) кўринишга эга бўлади. бу ерда ва Бу шакл функциялари 3.1 расмда кўрсатилган координаталар системасига нисбатан аниқланади. Бунда L элемент узунлиги. Энди (3.7) ва (3.9) даги матрицалар (3.12) шаклни олади. Шунинг учун 58 (3.13) л х Ж 3.1 - расм . Ч изиқли бир ў л ч овли элемент Материалнинг хоссаларини ифодаловчи матри ц а бита коеффи ц ентга келади : (3.14) (3.6) даги интегралларни ҳисоблаймиз: ( 3.15) Бунда к ўндаланг к ес и мнинг юзаси ўзгармас деб ҳисобланади. (3.16) Ч унки д S = P дх , бу ерда P - периметр. Периметр ҳам х  ўқи б ў йлаб ўзгармас деб ҳисоблан ган . (3.16) даги к ў пайтири шни бажариб ва интегрални ҳисобла б (3.17) ни хосил қиламиз. Элементнинг иссиқлик ўтказувчанлик матрицаси (3.5) ва (3.17) матрицаларни қўшиш орқали олинади: 59 (3.18) Агарда элементнинг чегарасида нолга тенг бўлса, (3.18) даги конвек ция ни ифодаловчи хад й ў қолади. Э лементнинг ку ч векторидаги (3.10)интегралларни ҳисобла ш қуйидагиларни беради: (3.19) ва (3.20) (3.10)даги учинчи интеграл шакл жиҳатидан иккинчиси билан бир хил бўлганлиги сабабли, биз дарҳол (3.21) ёзишимиз мумкин. Натижада учун тўлиқ ифода қуйидагича бўлади: (3.22) Ушбу ифоданинг кейинчалик йиғиндига киришини ҳисобга олиб, бу ифодани 60 (3.23) кўринишда ёзиб оламиз. Бир ўлчовли иссиқликни узатиш масаласига мисол қилиб стерженни совутиш муаммосини олиш мумкин. Бир учи иссиқлик манбаига уланган стерженни кўриб чиқамиз. Стерженнинг ён сиртларидан ва унинг бошқа учи орқали иссиқлик атроф-муҳитга чиқарилади (3.19) ва (3.23) формулалар конвекция ҳисобига иссиқлик йўқотилиши фақат ён сиртлар ҳисобига содир бўлишини назарда тутади. Энди бир ўлчовли элементнинг четларидан иссиқликни чиқиши билан боғлиқ бўлган муносабатларни кўриб чиқамиз. Фараз қилайлик, иссиқлик стерженнинг ўнг четидан тарқатилсин ( j тугун). Иссиқликнинг йўқолиши (оқиб кириши) ёки конвектив иссиқлик алмашинуви натижасида ёки маьлум иссиқлик оқими q  мавжудлиги сабабли содир бўлади. Шунинг учун фақат сирт интегралларини ҳисобга олиш керак. Иссиқлик ўтказувчанлиги матрицасидаги сирт интегралини кўриб чиқамиз: Бизни ж тугун қизиқтираётганлиги учун ва натижада бу миқдорларни интегралга қў йсак: ни ҳосил қиламиз ёки бундан (3.24) 61 бўлади. Агар эркин учида иссиқлик йўқотилиши содир бўлса, бу матрица (3.18) матрицалар йиғиндисига қўшилиши керак. Мутлақо тушинарлики, (3.24) даги иссиқлик алмашинуви коэффициенти ён сиртдаги коэффициентдан фарқ қилиши мумкин. матрицадаги сирт интеграллари (3.25) ва (3.26) кўринишларни олади. (3.24) - (3.26) формулалардан (3.18) ва (3.23) формулалар билан биргаликда фойдаланиш қуйидаги мисолда кўрсатилган. Мисол Қуйидаги физик хусусиятларга эга бўлган бир ўлчовли стержен температура тақсимотини ҳисоблаш талаб қилинади: Биз лойиҳани ҳар бири 1,5 см узунликдаги 5 та элементга ажратамиз. Биринчи тўртта элемент учун элемент матрицалари бир хил ва (3.18) ва (3.23) формулалар ёрдамида тузилиши мумкин. 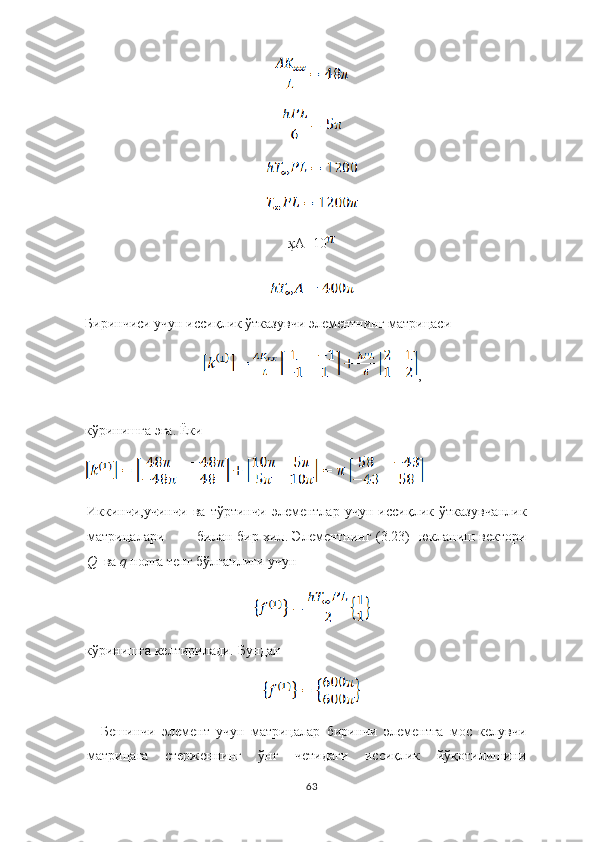Ушбу муносабатларга киритилган турли параметрларнинг қийматларини ёзамиз: 62 ҳ А=10 Биринчиси учун иссиқлик ўтказувчи элементнинг матрицаси , кўринишга эга. Ёки Иккин ч и,у ч ин ч и ва т ў ртин ч и э лементлар у ч ун иссиқлик ў тказув ч анлик матри ц алари билан бир хил . Элементнинг (3.23) юкланиш вектори Q ва q   нолга тенг бўлганлиги учун кўринишга келтирилади. Бундан Бешинчи элемент учун матрицалар биринчи элементга мос келувчи матрицага стерженнинг ўнг четидаги иссиқлик йўқотилишини 63 тавсифловчи шартларни қўшиш орқали олинади. Иссиқлик ўтказувчанлик матрицасини қуриш учун (3.24) даги ҳисоб-китобларнинг натижаларини га қўшиш керак. бўлгани учун қуйидаги матрица қўшилиши керак: ва Б ешинч и э лемент у ч ун ю к ланиш вектори ёки бўлади. Тўғридан-тўғри қаттиқлик усулини қўллангандан сўнг, тўплам элементларнинг кўриб ўтилган матрицалари тўплами қуйидаги тенгламалар системасига олиб келади: Бу ерда π га қисқартири ш амалга о ш ирил ган , ч унки у тенгламалар системаси нинг икала қисмига ҳам киради. [К] даги б ўш жойлар нол ко э ффи ци ентларни билдиради. нинг қиймати маьлум (150° C ), ш унинг у ч ун е ч и ш дан олдин тенгламалар системаси ни ў згартири ш (модификация) керак. У ш бу 64 ў згартири ш ў нг томондаги устунни ш аклга айлантиради. Системани ечгандан сўнг ни ҳосил қиламиз. Температура нинг н азарий қийматлари эса [2] қуйидаги ч а: Ч екли э лементлар усулида олинган натижалар, соҳа бир хил э лементларга б ў линганлигини ҳисобга олсак, ҳақиқий қийматларга я х ш и мос келади. Агарда стержен ўрнатилган девор яқинида қисқароқ элементлардан фойдаланиш орқали ч екли э лементлар усулида олинган ечимни яхшилаш мумкин. Олдинги мисолда стерженнинг кўндаланг кесими ўзгармас эди. Бу талаб мажбурий эмас. Кесим юзаси элементнинг узунлигига ҳам боғлиқ бўлиши мумкин. Агар элементнинг юзаси узунлик бўйлаб ўзгарса, у ҳолда элемент матрицаси ўзгартирилиши керак. Мана шу ўзгартиришни муҳокама қиламиз. 3.2 -расм . кесими ўзгарувчи бўлган бир ўлчовли элемент . 3.2 расмда к ў рсатилган э лементни к ў риб ч иқайлик . Унинг кўндаланг кес и м ининг юзас и ч ап у ч и дан ў нг у ч идаги га ч а ў згариб туради . Агар да биз юза нинг ч изиқли ў згари ш и билан ч еклансак , юзага (3.27) муносабатни ё зи ш имиз мумкин . Бу ерда ва чизиқли ш акл функ ция лари дир. 65 Кейинги қадам элемент матрицаларини аниқлашдир. ни ҳисоблаш учун (3.15) формуланинг биринчи қисмидан фойдалансак (3.28) ни ҳосил қиламиз. Бу формуладаги А нинг қиймати х  бўйлаб ўзгармас бўлмаганлиги учун унинг теграл белгисидан чиқариб бўлмайди. (3.27) ифодани (3.28) га қўйиш қуйидагини беради: Буни и нтеграллаш орқали н и ҳосил қиламиз, бундан (3.29) ни биз оламиз . ўртача элемент юзасига тенг бўлганлиги учун (3.29) ифодани қуйидагича ёзиш мумкин. (3.30) Бу ерда – ўртача юза. (3.30) формула (3.15) билан юзани ўртача қийматга алмаштириш аниқлигича устма-уст тушади . Ён сиртлар бўйича олинган интеграллар ҳам худди шундай тарзда ифодаланиши мумкин. Периметрни (3.31) 66 муносабат сифатида ёзиш мумкин. Натижада (3.32) ни ҳосил қиламиз ва ларнинг қийматларини қўйиб ва интеграл ҳисоблангандан кейин (3.33) ҳосил бўлади. Сирт интеграллари эса (3.34) (3.34) муносабатлар билан тасвирланади. (3.30) ва (3.34) матрицаларни қўшиб, биз ни ҳосил қилишимиз мумкин. (3.35) муносабат нинг қисмини беради. (3.34) ва (3.35) формулалардан кўриниб турибдики, уларни (3.17) ва (3.21) формулалардан конуссимон элемент ҳолатида ўртача периметрни оддий алмаштириш йўли билан олиш мумкин эмас. 3.3 Икки ўлчовли иссиқлик узатиш Икки ўлчовли иссиқлик ўтказувчанлиги муаммоларини ҳал қилиш учун учта тугунли учбурчак элемент кенг қўлланилади. Ушбу элемент доира кесимлар бўлмаган стерженнинг буралишини кўриб чиқишда аллақачон ишлатилган [1]. Шунинг учун ҳам [1]даги баьзи бир натижалардан 67 фойдаланишимиз мумкин. Чизиқли учбурчак элемент учун шакл функциялари қуйидаги кўринишда бўлар эди, б уерда (1 - бобда) да аниқланган : (3.36) Температура (3.37) формула бўйича аниқланади. Бу ерда –температуранинг кетма-кет тугунлардаги қийматлари бўлиб, i  тугундан соат стрелкаси йўналишига тескари йўналишда ўтади. [ ] градиент лар матри ц асини ва материал хоссалари матрицаларини ё замиз: (3.38) (3.39) натижада элементнинг иссиқлик ў тказув ч анлик матри ц асини ҳисобла ш имиз мумкин. Бирин ч и қўшилувчи 68 (3.40) Ш аклни олади . Элементнинг қалинлигини бир га тенг деб ҳисоблаб, ни дА  билан алма ш тирамиз. (3.40) даги интеграл остидаги ифода ўзгармас ва уни интеграл белгиси остидан ташқарига чиқариш мумкин : (3.41) Матритсалар ни кўпайтиришни ҳисоблаб (3.42) ни ҳосил қиламиз. Иккинчиинтеграл сиртбўйича ҳисобланишикерак. 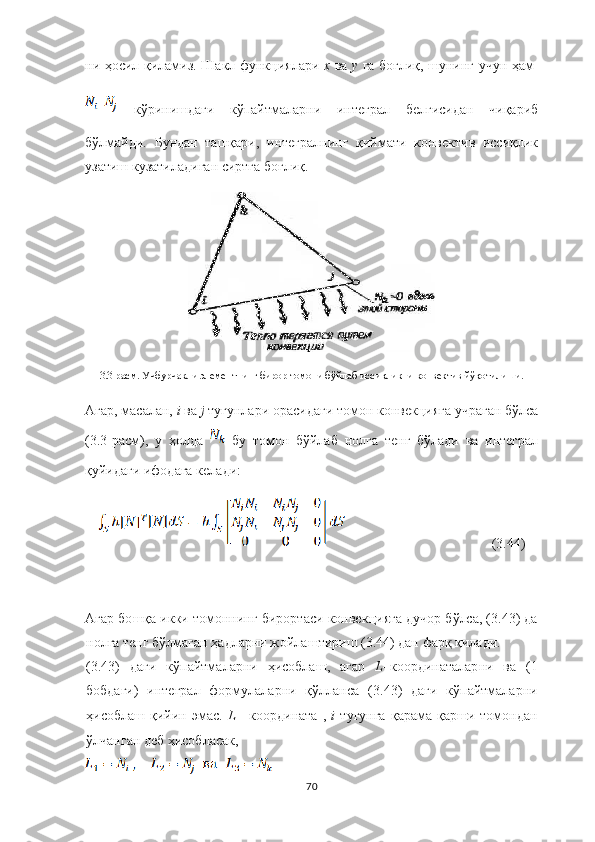матрицагашакл функцияларини қўйиб , матрицаларни кўпайтириб (3.43) 69 ни ҳосил қиламиз. Шакл функциялари х  ва у   га боғлиқ, шунинг учун ҳам кўринишдаги кўпайтмаларни интеграл белгисидан чиқариб бўлмайди. Бундан ташқари, интегралнинг қиймати конвектив иссиқлик узатиш кузатиладиган сиртга боғлиқ. 3.3 расм . Учбурчакли элементнинг бирор томони бўйлаб иссиқликни конвектив йўқотилиши . Агар, масалан, i   ва j   тугунлари орасидаги томон конвекцияга учраган б ў лса (3.3-расм), у ҳолда бу томон бўйлаб нолга тенг б ў лади ва интеграл қуйидаги ифодага к ела ди: (3.44) Агар бо ш қа икки томоннинг бирортаси конвек ц и я га ду ч ор б ў лса, (3.43) да нолга тенг б ў лмаган ҳадларни жойла ш тири ш (3.44) дан фарқ қилади. (3.43) даги кўпайтмалар ни ҳисобла ш , агар L –координаталар ни ва (1 бобдаги) интеграл формулаларни қўлланса (3.43) даги кўпайтмаларни ҳисоблаш қийин эмас. L координата , i   тугунга қарама-қар ш и томондан ў л ч анган деб ҳисобласак, 70 деб ё зи ш имиз мумкин . Агар конвектив иссиқлик узатиш i    ва j   тугунлари орасидаги томон бўйлаб амалга ошишини фараз қилсак, бу томоннинг сиртида элементнинг тугунлари орасидаги содир б ў лади деб фараз қилсак , у ҳолда ва (3.44) муносабат (3.45) кўринишни олади, бу ерда ҳамда t қалинлик бирга тенг деб ҳисобланади. (3.45) формулада икки хил типдаги кўпаймалар мавжуд: квадратлар ҳамда аралаш кўпайтмалар. Квадратли ҳадларни ҳисоблаймиз: Бу ерда I  в а     j  тугунлар орасидаги томоннинг узунлиги. Аралаш кўпайтмали ҳадларнинг интеграли учун ни ҳосил қиламиз. интеграл ва лар ўзаро бир-бирига тенг. Олинган натижаларни (3.45) формулага қўйиб , (3.46а) 71 ни ҳосил қиламиз. Шунга ўхшаш муносабатлар ва к  тугунлар орасидаги томон учун ҳам ўринли: (3,46б) ҳамда к   ва i   тугунлар орасидаги томон учун ҳам ўринли: (3.46в) Агар L   –координаталардан фойдаланилса, элементнинг юкланиш вектори ифодасидаги учта интеграл ҳам осон ҳисобланади. ни ҳисоблашдан бошлаймиз. Фараз қилайлик элемент ичида Q ўзгармас бўлсин, у ҳолда (3.47) га эга бўламиз. Шундай қилиб элементдаги иссиқлик ҳар бир тугун учун тенг тақсимланади. ваинтеграллари бир хил шаклда ёзилади: (3.48) Шунинг учун улардан фақат биттасини ҳисоблаш етарли. (3.48) сирт интеграли бўлгани учун, уни ҳам (3.43) интеграл каби кўриб чиқиш мумкин. Натижалар элементнинг h   миқдор билан характерланувчи қайси томони бўйлаб конвектив иссиқлик алмашинуви содир бўлишига ёки q 72 иссиқлик оқими ҳисобига иссиқликни қуйилишига боғлиқ бўлади. Элемент сирти бўйлаб қ ўзгармас деб фаразқилсак, (3.48) интегралнинг қуйидагтучта шаклни ҳосил қиламиз: Қиймат q ни алмаштиришни ҳисобга олган ҳолда (3.49а) - (3.49в) билан бир хил. Агар иссиқлик оқими ёки конвектив иссиқлик алмашинуви элементнинг икки томонида кузатилса, у ҳолда сирт интеграли томонларнинг ҳар бир томон бўйича олинган интеграллар йиғиндиси билан алмаштирилади. Худди шунарса (3.43) интеграл учун ҳам амал қилади. Кўпгина иссиқлик узатиш муаммоларида тугун нуқталаридаги температураларни қийматлари қизиқтиради. Баьзан температура градеантларининг аниқлаш зарурати туғилади. Тугун қийматлари аниқлангандан сўнг, температура градиентлари (3.50) Боғланишдан фойдаланиб топилади. Қуйидаги сонли мисол юқорида олинган муносабатларни қўллашни кўрсатади. 73 Мисол Қуйида туташ муҳитни дискретлаштириш учун фойдаланиладиган элемент келтирилган. Ушбу элементнинг иккита сирти бўйича конвектив иссиқлик алмашинуви содир бўлади. Элементнинг ўлчамлари ва физик хусусийатлари кўрсатилган. Элементнингқалинлигинибирга тенгдебҳисоблаганҳолда, унинг элемент матритсаларини тузиш талаб қилинади. Элементнинг иссиқлик ў тказув ч анлик матри ц асини қараймиз : ва c   константалари формулалар б ў йи ч а ҳисобланади 74 томонларининг узунликлари тенг =4.12 см =3.16 см Топилган сонли қийматларни га қўйсак ёки Элемент юкланиш вектори конвектив иссиқлик алма ш инуви содир б ў лаётган икки томон бўйича сирт интегралларининг йи ғ индисидир: 3.4. Иссиқлик узатишнинг уч ўлчовли ҳоли Иссиқлик узатишнинг уч ўлчовли масалалардаги элемент учун муносабатларни келтириб чиқариш бир ўлчовли ва икки ўлчовли ҳоллардаги мос келадиган процедураларга айнан ўхшаш. Дискретизация 75 элементи сифатида тўртта тугунли тетраэдрни кўриб чиқамиз. Бу ҳолатга мос келадиган шакл функцияси (3.51) кўринишда бўлади. Бу ерда ўзгармаслар 1-бобда кўрсатилганидек детерминантлардан фойдаланиб ёки матритсаларни кўпайтмасидан фойдаланибҳисобланади. Зарур бўлган матрицаларни ёзамиз (3.52) (3.53) Агар ҳажмли L -координаталардан фойдаланилса, интегралларни ҳисоблаш жуда осон Интегралларни ҳисоблаш қуйидаги натижаларни беради: (3.54) 76 (3.55) (3.56) (3.57) (3.55) интеграл учун учта бошқача ёзув шакли мавжуд бўлиб, улар ҳар бир қолган томон учун биттадан мос келади. Улардагиҳарбирининг бош диагоналдаги коэффициентларнингқийматлари иккига тенг ва бош диоганалдан ташқари коэффициентларнинг нолмас қийматлари бирга тенг. Кўриб чиқилаётган сиртдан ташқарида жойлашган тугунлар нуқталарга мос келадиган сатр ва устунлардаги коэффициентлар нолга тенг. (3.57) интеграл учун ҳам учта ёзув шакли мавжуд. Нол коэффициент қаралаётган сиртдан ташқарида ётган тугунга мос келадиган сатрда жойлашади. - I,j,k  тугунларни ўзида сақловчи сиртнинг юзаси. 3.6 Нуқтали иссиқлик манбалари Шу пайтгача кўпгина физик масалалар учун муҳим бўлган нуқта ёки чизиқли манбалар тушунчаларини кўриб чиқмаган эдик. Агарда Q иссиқлик генерацияси Жуда кичик ҳажм ёки жуда кичик юза ичида содир бўлса, у ҳолда нуқтали(чизиқли) иссиқлик манбаи мавжуд дейилади. Чизиқли манбаларга мисол қилиб иссиқ сув ва (ёки) буғ бериш учун ерга ётқизилган қувурлар ва электр ўтказувчан муҳитда ўтказгич симларини олиш мумкин. Ушбу ҳолатларнинг ҳар бирида қувур ёки симнинг 77 кўндаланг кесим юзаси атроф-муҳит ўлчамларига нисбатан анча кичикдир. Ерости сувларини оқиши масаларида сувларни тортиб олувчи насосларни ҳам нуқтали манба сифатида қараш мумкин. Нуқтали ва чизиқли манбалар ҳаётимизда кўп учрайди ва эьтиборга моликдир 3.4 - расм . Уч ўлчовли элемент ичидаги нуқтали манба . Биз икки ў л ч овли элемент и ч ида жойлашган нуқтали манбани муҳокама қилиш билан ч екланамиз, лекин муҳокама қилинадиган амалларни у ч ў лчовли элемент лар га ҳам тарқатиш мумкин. ( ) нуқтада жойлашган Q* [кВт/м] чизиқли манбага эга бўлган учбурчакли элементни қараймиз (3.4 расм) (иссиқлик ичкарига кирадива мусбат ҳисобланади). Иссиқлик манбаи нуқтада жойлашганлиги сабабли, Q  энди ҳажм ичида ўзгармас эмас балки , х   ва у   координаталарининг функциясидан иборат бўлади. [1] бирлик импульс функциялардан фойдаланиб қуйидагича ёзиш мумкин. (3.59) У ҳолда интегрални қуйидагича ё зи ш мумкин : (3.60) 78 Элементнинг қалинлиги бирга тенг деб ҳисобланади. Импул ь с функ ц и я ларининг маьлум хусуси я тларидан фойдаланиб қуйидаги мунособатни ҳосил қиламиз: (3.61) Муносабат шуни кўрсатадики, агар нуқтали (чизиқли) манба элемент ичида жойлашган бўлса, Q   нуқта манбасининг координаталари ёрдамида ҳисобланган тегишли ва қийматларига пропорционал равишда тугунлар бўйлаб тақсимланади. Элементнинг исталган нуқтасида бўлгани учун биз Q* дан катта қийматни олмаймиз. Мисол. Манба интенсивлиги Q *=52 Вт/см. Манба Q * қуйида кўрсатилган координаталари (5;2) бўлган нуқтада жойлашган. Тугун нуқталари бўйича Q *тақсимотини аниқлаш талаб қилинади. Бундан олдинги мисолда ва қийматлари ҳисобланган: 79 ўзгармасларни ҳисоблаймиз : 2 А =13 муносабат э канлигини ҳисобга олсак , у ч ун муносабатларни қуйидаги ч а қайта ё зи ш мумкин : Бу ерга ларни қўйиб қуйидагини ҳосил қиламиз Қ * миқдорнинг қиймати, и , ва тугунлар да мосрави ш да қисмларгабўлинади. Демак, буэлементу ч ун интеграл Га тенг. Узлуксиз муҳит элементларга бўлинишда,тугунлардан бирига нуқта (чизиқли) манба жойлаштирилиши мумкин. Бу (3.63) ифодани интеграллашни соддалаштиради Фараз қилайлик, манба –тугунда жойлашган (3.5-расм), у ҳолда ва (3.62) Сўнгра (3.62) даги Q * манба биттадан кўп элементларга тегишли эканлигини ҳисобга олган ҳолда ўзгартирилиши керак.Манбанинг 80 интенсивлик қиймати тугунни ўраб турган элементлар бўйича тақсимланиши керак. 3.5 – расм. Тугун нуқталари Бу тугун дажойлашган элементнинг учи 360° нинг қандай қисмига мос келишига қараб тақсимлаш амалга оширилади. 3.5 расмдаги (е) элемент учун тўғри муносабат (3.63) кўринишда бўлади. Бироқ тугундаги манбани ўраб турган турли элементлар учун бурчагини ҳисоблашнинг ҳожати йўқ. Айрим элементлар учун тенгламалар тўғридан-тўғри қаттиқлик усули ёрдамида бирлаштирилгандан сўнг, ушбу элементга тегишли барча элементларнинг қўшма ҳиссаси Q* нинг умумий қиймати бўлади. Тугун манбасини ҳисобга олишнинг оддий усули глобал юкламанинг {Ф} векторига, тўғрироғи унинг шу тугунга мос келувчи эркинлик даражасининг компонентасига Q * қийматини қўшишдир. Уч ўлчовли элемент бўлган ҳолда, элемент ичидаги локаллаштирилган манба тўртта тугунга мос (3.59) 81 формула бўйича тақсимланади. Бу ерда ( ) -  манба жойлашиш нуқтасининг координаталари. 82 ХУЛОСА Диссертация иши ёрдамида жисмдаги температурани тақсимлашнинг мақсад ва вазифалари билан боғлиқ ҳолда қуйидаги натижаларга эришилди: 1. Агар температура тақсимоти маьлум бўлса, жисмга бериладиган ёки йўқотадиган иссиқлик миқдорини ҳисоблаш мумкин. 2. Температура майдони кучланишларнинг тақсимланишига таьсирқилади. Иссиқлик кучланишлари температура градиентлари мавжуд бўлган ва барча йўналишларда эркин тарқала олмайдиган ҳар бир жисмда содир бўлади. Реактив двигателлар ёки буғ генераторлари каби айланадиган машиналарни лойиҳалашда ушбу кучланишларни ҳисобга олиш зарур. 3. Иссиқлик кучланишларини ҳисоблаш учун биринчи навбатда жисмдаги температура тақсимотини аниқланди. 4. Тадқиқотда аниқ моделлар мисолида иссиқлик кучланишлари ва температура тақсимотини аниқлаш усуллари чекли элементлар усули ёрдамида кўрсатиб ўтилди. Ҳисоблашлар бир ўлчовли, икки ўлчовли ва уч ўлчовли ҳоллар учун алоҳида алоҳида бажарилди. 5. Тадқиқотда нуқтали (чизиқли) иссиқлик манбаи берилган ҳолда ҳам температура тақсимотини топиш усуллари кўрсатилди. 83 Адабиётлар 1. Сегерлинд Л. Применение ме тода конечных элементов.Из- во” Мир ”,Москва 1979. 2. Зенкевич О.,Морган К. Конечные элементы и аппроксимация. Из-во ” Мир ”, Москва 1986. 318 с. 3. Зенкевич О.Метод конечных элементов и технике. М.: Мир ,1975. 4. Деклу Ж. Метод конечных элементов Из-во ” Мир ”, Москва 1976. 5. Сьярле Ф.Метод конечных элементов для эллиптических задач Из- во ” Мир ”, Москва 1980 Метод . 6. Норрн.Д,де Фриз Ж .Введение в метод конечных элементов Из-во ” Мир ”, Москва 1981. 7. Галлагер Р. Конечные элементы.Основы. Из-во ” Мир ”, Москва 1984. 8. Макаров Е.Г. «Сопротивление материалов с использованием вычислительных комплексов», книга 1. 9. Н.И.Березовский, С.Н.Березовский, Е.К.Костюкевич. Технология энергосбережения: учеб.пособие / Н.И.Березовский, С.Н.Березовский, Е.К.Костюкевич. – Минск: БИП-С Плюс, 2007. – 152с. 10. Г.И.Саркисов. Справочник к курсовым и расч×тно-графическим работам по курсу«Теплопередача». 11. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача: учебник для вузов, Изд. 3-е, перераб. и доп.– М. : Энергия, 1975. – 488с. 12. МихеевМ.А.,МихееваИ.М.Основы теплопередачи. Изд.2-е, стереотип. М., «Энергия», 1977. 13. РавичМ.Б.Топливоиэффективностьего использования. Изд-во «Наука», 1971,1-358. 14. Самойлов М.В. Основы энергосбережения. Учеб. Пособие / М.В.Самойлов, В.В. Паневчик, А.Н.Ковалев. – Мн.: БГЭУ, 2002. – 198 с. 84 15. В.А. Пашинский, Е.В.Кресова Учебно-методический комплекс по учебной дисциплине «Теплопередача» 85

Иссиқ ли қ ў тказувчанлик ва конвекция ҳ исобидан исси қ лик к ў чиши жараёнининг баьзи математик моделларини тад қ и қ этиш МУНДАРИЖА Кириш………………………………….………………………………………..3 I БОБ. Чекли элементлар усули ва унинг баьзи бир чегаравий масалаларга тадбиқи….........................…………….………………… ………………….. ....7 II БОБ. Иссиқлик ўтказувчанлик назариясининг асосий тушунчалари ………………………….……………………… ………… …….… ………. …..22 III БОБ. Иссиклик утказувчанлик ва конвекция хисобидан иссиклик кучиши жараёнининг баьзи математик моделларини тадкик этиш ………………………………………………………………..…...…… ..53 ХУЛОСА………..……………………………………… . ………………..…...78 АДАБИЁТЛАР……………………………………………… . ……………......79 ИЛОВАЛАР.......................................................................................................83 1

2

КИРИШ Чекли элементлар усули физика ва техникада учрайдиган дифференциал тенгламаларни сонли ечиш усули ҳисобланади. Бу усулнинг пайдо бўлиши космик тадқиқотларни ҳал қилиш муаммолари билан боғлиқ (1950). Бу иш биринчи марта Тёрнер, Клуж, Мартин ва Топп томонидан нашр э тилган [4]. Бу бошқа ишлар нинг пайдо бўлиши га туртки бўлди ; чекл и э лемент лар усули ни қурилиш механикаси ва туташ муҳитлар механикасига татбиқ қилинган бир қатор мақолалар чоп э тил ди. Усулни назарий асослаш учун 1963 йил Мелош [2] муҳим ҳисса қушди. У чекли элементлар усулини Рэлей-Ритц усулининг вариантларидан бири эканлигини кўрсатди. Қурилиш механикасида чекли элементлар усули потециал энергияни минималлаштириш орқали масалани мувозанатнинг чизиқли тенгламалар системасига келтириш имконини беради. Чекли элементлар усулининг минималлаштиришга боғлиқлиги унинг техниканинг бошқа соҳаларидаги муаммоларини ҳал қилишда фойдаланишга олиб келди. Усул Лаплас ёки Пуассон тенгламалари билан тавсифланган муаммоларга нисбатан ҳам қўлланилди. Бу тенгламаларни ечиш ҳам бирор функционални минималлаштириш билан боғлиқ. Дастлабки нашрларда [6, 7] чекли элементлар усули ёрдамида иссиқлик тарқалиш масалалари ечилди. Сўнгра бу усул гидромеханика муаммоларига, хусусан, ғовакли муҳитда суюқлик оқими муаммосига нисбатан қўлланилди. Қурилиш механикаси, иссиқлик тарқалиши, гидромеханика масалаларида элементларни аниқловчи тенгламалар вазнли тафовутлар усулининг вариантларидан бири бўлган Галёркин ёки энг кичик квадратлар усули ёрдамида осонгина ҳосил қилиш мумкинлиги исботлангандан [3, 8] сўнг чеклиэлементлар усулининг қўлланиш соҳаси сезиларли даражада кенгайди. Бу фактнинг ўрнатилиши чекли элементлар 3

усулини назарий асослаш учун муҳим рол ўйнади натижада, бу усулни ихтиёрий дифференциал тенгламани ечишга қўллаш имконини берди. Шундай қилиб чекли элементлар усули қурилиш механикаси муаммоларини сонли ечиш усулидан дифференциал тенгламаларни ёки дифференциал тенгламалар системасини сонли ечишнинг умумий усулига айланди. Бу ривожланишга тезкор сонли ҳисоблаш машиналарининг мукамаллашуви ҳисобига 15 йил давомида эришилди. Тадқиқоднинг мақсади. Ушбу диссертациянинг мақсади чекли элементлар усулининг бир ўлчовли, икки ва уч ўлчовли иссиқлик ўтказувчанлик масалалари билан боғлиқ бўлган қирраларини мухокама қилишдан иборат. Чекли элементлар усулининг асослари билан бирга ушбу методнинг ЭҲМда бажариш масалалари ҳам қаралади. Тадқиқод масаласи. Диссертация ишида иссиқлик ўтказувчанлик масалаларига доир мақсад ва вазифалардан келиб чиқиб mathcad математик пакетидан фойдаланиб қуйидаги масалалар тадқиқ қилинади : 1. Бирор жисмга киритилаётган ёки ундан чиқаётган иссиқлик миқдорини температура тақсимоти берилганда ҳисоблаш. 2. Температура майдони кучланиш тақсимотига таьсир қилади. Температура градиенти мавжуд ва барча йўналишлар бўйича эркин тарқала олмайдиган ҳар бир жисмда температура кучланиши вужудга келади. Бу кучланишни айланувчи механизмлар (м.н реактив двигателлар ёки буғ генераторлари)ни лойихалаштириш пайтида албатта ҳисобга олиш зарур. 3. Температура кучланишини ҳисобга олиш учун энг аввало жисмдаги температура тақсимотини аниқлаш керак. Тадқиқоднинг обьекти ва предмети. Иссиқлик инсон ҳаётида, жумладан унинг организмининг фаол ишлашида муҳим рол ўйнайди. Озиқ-овқат таркибида бўлган кимёвий энергиянинг бир қисми иссиқликка 4

айланади ва бунинг натижасида инсон жисмсининг температураи 37 атрофида сақлаб турилади. Инсон жисмидаги температура баланси атроф муҳитга ҳам боғлиқ ва инсонлар қишда ишлаб чиқариш ва яшаш хоналарини иситиш учун ва ёзда совутиш учун кўп энергия сарфлашга мажбур бўлишади. Бу энергиянинг кўп қисмини иссиқлик машиналари, масалан қозон қурилмалари ва ёқилғи қазилмалари (кўмир, нефт)да ишлайдиган ва электр энергияси ишлаб чиқарадиган электростанцияларнинг буғ трубиналари етказиб беради. Иссиқлик алмашинуви ёки иссиқлик узатиш – бу жисм ичидаги ёки температуралар фарқига эга бўлган бир жисмдан иккинчи жисмга иссиқликни узатиш жараёнидир. Иссиқликни узатиш моддаларнинг хусусиятларига, температуралар фарқига ва табиатнинг экспериментал ўрнатилган қонунларига бўйсунади. Самарали ишлайдиган иссиқлик ёки совутиш тизимларини, ҳар хил двегателларни энергия қурилмаларини иссиқлик изоляция тизимларини яратиш учун иссиқлик узатишнинг талабларини билиш керак. Баьзи холларда иссиқлик алмашинувига эҳтиёж кам (космик кемаларда), баьзи холларда эса эҳтиёж кўп сезилади(буғ қозонлари, ошхона идишлари). Тадқиқод усуллари. Чекли элементлар усулининг минималлаштириш процедураси билан боғлиқлиги уни техниканинг бошқа соҳалардаги масалаларни ечишда ҳам кенг қўлланилишига олиб келди. Бу Лаплас усули ёки Пуассон тенгламалари билан тавсифланган масалаларга ҳам қўлланилади. Шу билан бирга бу тенгламаларни ечиш бирор функционални минималлаштириш билан боғлиқдир. Дастлабки нашрларда [6,7] чекли элементлар усули ёрдамида иссиқлик тарқалиш масалаларига тадбиқ қилинди. Сўнгра бу усул гидромеханика масалаларига, хусусан ғовак жисмларда суюқликни оқиш масалаларига қўлланила бошланди. 5

O'xshashlar

ЧЕКЛИ ЭЛЕМЕНТЛАР УСУЛИ ЁРДАМИДА ДИФФЕРЕНСИАЛ ТЕНГЛАМАЛАРНИ ЕЧИШ
НОМУТАХАССИС ТАЪЛИМ ЙЎНАЛИШЛАРИ УЧУН АХБОРОТ ТЕХНОЛОГИЯЛАРИДАН МУЛЬТИМЕДИАЛИ ДИДАКТИК ВОСИТАЛАРНИ ШАКЛЛАНТИРИШ МЕХАНИЗМЛАРИ
ҚОВУШҚОҚ-ЭЛАСТИК ПЛАСТИНКА ЭГИЛИШИ МОДЕЛИНИ СОНЛИ ТАДҚИҚ ЭТИШ
УМУМИЙ ЎРТАТАЪЛИМ МАКТАБЛАРИДА ОРГАНИК КИМЁ ФАНИНИ ЎҚИТИШДА ИННОВАЦИОН УСУЛЛАРДАН ФОЙДАЛАНИШ
ОЛИЙ ТАЪЛИМ МУАССАСАЛАРИДА НИЗОЛИ ВАЗИЯТЛАР ПРОФИЛАКТИКАСИНИНГ ТАШКИЛИЙ-ПЕДАГОГИК ШАРТ-ШАРОИТЛАРИНИ ТАКОМИЛЛАШТИРИШ