Minimal kenglikdagi daraxt Kruskal algoritmi






![MSTda 3-4 chekka qo'shing
Eslatma: MSTga kiritilgan qirralarning soni ( N – 1) ga teng bo lgani uchunʻ
algoritm shu yerda to xtaydi.
ʻ
2.3 Kruskal algoritmiga oid C++ dasturlash tilida dastur.
#include <bits/stdc++.h>
using namespace std;
class DSU {
int* parent;
int* rank;
public:
DSU(int n)
{
parent = new int[n];
rank = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = -1;
rank[i] = 1;
}
12](/data/documents/1c33a4b2-80aa-448c-91ba-f89d8dc2f794/page_12.png)
![}
int find(int i)
{
if (parent[i] == -1)
return i;
return parent[i] = find(parent[i]);
}
void unite(int x, int y)
{
int s1 = find(x);
int s2 = find(y);
if (s1 != s2) {
if (rank[s1] < rank[s2]) {
parent[s1] = s2;
}
else if (rank[s1] > rank[s2]) {
parent[s2] = s1;
}
else {
parent[s2] = s1;
rank[s1] += 1;
}
}
}
};
class Graph {
vector<vector<int> > edgelist;
int V;
public:
Graph(int V) { this->V = V; }
void addEdge(int x, int y, int w)
{
edgelist.push_back({ w, x, y });
}
void kruskals_mst()
{
13](/data/documents/1c33a4b2-80aa-448c-91ba-f89d8dc2f794/page_13.png)
![sort(edgelist.begin(), edgelist.end());
DSU s(V);
int ans = 0;
cout << "Following are the edges in the "
"constructed MST"
<< endl;
for (auto edge : edgelist) {
int w = edge[0];
int x = edge[1];
int y = edge[2];
if (s.find(x) != s.find(y)) {
s.unite(x, y);
ans += w;
cout << x << " -- " << y << " == " << w
<< endl;
}
}
cout << "Minimum Cost Spanning Tree: " << ans;
}
};
int main()
{
Graph g(4);
g.addEdge(0, 1, 10);
g.addEdge(1, 3, 15);
g.addEdge(2, 3, 4);
g.addEdge(2, 0, 6);
g.addEdge(0, 3, 5);
g.kruskals_mst();
return 0;
}
Dasturning natijasi.
Quyida tuzilgan MSTning qirralari keltirilgan
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
Minimal xarajat yoyilgan daraxt: 19
14](/data/documents/1c33a4b2-80aa-448c-91ba-f89d8dc2f794/page_14.png)

![MSTga tanlangan chekka qo'shing, agar u hech qanday tsiklni hosil
qilmasa.
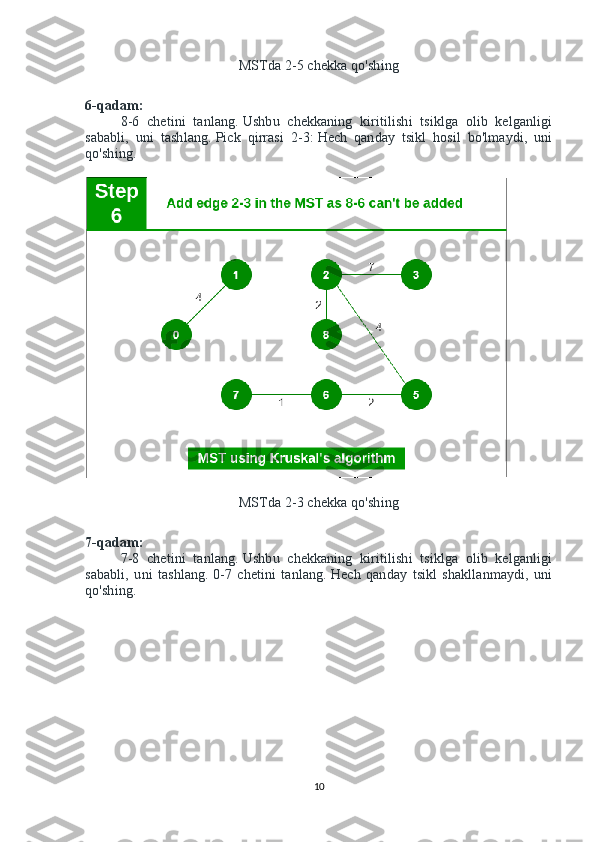
6-qadam:
MSTni qaytaring va chiqing .
Prim algoritmining tasviri:
Prim algoritmiga oid C++ dasturlash tilida dastur.
#include <bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 5
// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
int minKey( int key[], bool mstSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for ( int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// A utility function to print the
// constructed MST stored in parent[]
void printMST( int parent[], int graph[V][V])
16](/data/documents/1c33a4b2-80aa-448c-91ba-f89d8dc2f794/page_16.png)
![{
cout << "Edge \tWeight\n";
for ( int i = 1; i < V; i++)
cout << parent[i] << " - " << i << " \t"
<< graph[i][parent[i]] << " \n";
}
// Function to construct and print MST for
// a graph represented using adjacency
// matrix representation
void primMST( int graph[V][V])
{
// Array to store constructed MST
int parent[V];
// Key values used to pick minimum weight edge in cut
int key[V];
// To represent set of vertices included in MST
bool mstSet[V];
// Initialize all keys as INFINITE
for ( int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false ;
// Always include first 1st vertex in MST.
// Make key 0 so that this vertex is picked as first
// vertex.
key[0] = 0;
// First node is always root of MST
parent[0] = -1;
// The MST will have V vertices
for ( int count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the
// set of vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true ;
// Update key value and parent index of
17](/data/documents/1c33a4b2-80aa-448c-91ba-f89d8dc2f794/page_17.png)
![// the adjacent vertices of the picked vertex.
// Consider only those vertices which are not
// yet included in MST
for ( int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent
// vertices of m mstSet[v] is false for vertices
// not yet included in MST Update the key only
// if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == false
&& graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// Print the constructed MST
printMST(parent, graph);
}
// Driver's code
int main()
{
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// Print the solution
primMST(graph);
return 0;
}
// This code is contributed by rathbhupendra
Chiqish
Kenar og'irligi
0 - 1 2
1 - 2 3
0 - 3 6
1 - 4 5
18](/data/documents/1c33a4b2-80aa-448c-91ba-f89d8dc2f794/page_18.png)






Minimal kenglikdagi daraxt: Kruskal algoritmi Mundarija KIRISH ASOSIY QISM 1.Ma’lumot: 1.1. Minimal kenglikdagi daraxt haqida tushuncha 2. Amaliy : 2.1. Krusakal algaritmi 2.2 . Kruskal algoritmiga kirish 2.3. Krusakal algartmlari C++ dasturlash tilda ifodalash 2.4. Dasturni murakkabligini baholash 2.5. Minimal kenglikdagi daraxt uchun Prim algoritmi 2.6 Prim va Kruskal algoritmlar o’rtasidagi farqlari 2.7. Minimal kenglikdagi daraxt uchun Boruvka algoritmi 2.8. Minimal kenglikdagi daraxt uchun teskari o'chirish algoritmi Xulosa Foydanilgan adabiyotlar 1
Kirish Bugungi kunda mamlakatimizda axborot-kommunikatsiya texnologiyalarini qo‘llamaydigan korxonalar deyarli qolmadi va ulardan aksariyatining hozirgi vaqtdagi muammosi u yoki bu jarayonlarni avtomatlashtirilmaganligida emas, balki uzoq muddatli rejalarsiz amalga oshirilgan, ko‘r-ko‘rona avtomatlashtirish oqibatidir. Hisoblash texnikasi va dasturiy ta'minotni rejasiz xarid qilish, mayda kompaniyalarda yangilanmaydiga biznes takliflarga buyurtma berilishi va ularning joriy etilishi, turli bo‘linmalarga joriy etilgan bir vazifani hal etish uchun turli takliflarning mavjudligi, har xil segmentlangan tarmoqlarni ma'muriylashtirish va himoyalash muammolari — bularning barchasi turli kompaniyalar axborotkommunikatsiya texnologiyalar bo‘linmalari rahbarlari duch keladigan muammolar jumlasiga kiradi. AKTning rivojlanishi raqamli va matnli axborotga ishlov berishning barcha texnik vositalarini firma ichidagi yagona axborot tizimiga birlashtirish imkonini berdi. Bir vaqtning o‘zida hisoblash texnikasi va matnli axborotlarga avtomatlashtirilgan tarzda ishlov berish vositalaridan foydalanishga asoslangan axborot tizimi eng samarali hisoblanmoqda.Korxona faoliyati mobaynida ko‘p hajmdagi axborotlarni to‘playdi, ularni tezda qidirib topish esa ushbu axborot samarali joylashtirilgan va saqlangan taqdirda mumkin bo‘ladi. Ma'lumotlar bazasi firmaning ishlab chiqarish-sotish bo‘linmalarining xo‘jalik faoliyatini tavsiflovchi statistik ko‘rsatkichlar majmuini, shuningdek, firma rivojlanishining holati va tendensiyalariga ta'sir ko‘rsatuvchi barcha omillarga nisbatan materiallarni o‘z ichiga oladi. Ma'lumotlar bazasi uchun statistik ko‘rsatkichlar to‘plami puxta ishlab chiqiladi va firmaning faoliyat ko‘rsatishi natijalari va istiqbollarini chuqur iqtisodiy tahlil qilish uchun zarur bo‘lgan ko‘rsatkichlarni qamrab oladi. Odatda ma'lumotlar bazasini shakllantirishda ma'lumotlarni saqlash va yangilash tizimi to‘g‘risidagi masala ham hal etiladi. 2
1.1 Minimal kenglikdagi daraxt haqida tushuncha Eng kichik uzunlikdagi daraxt – berilgan grafning eng kam darajaga ega bo lgan daraxti, bu yerda daraxtning darajasi uning qirralari daajalari yig indisiʻ ʻ sifatida tushuniladi. Misol. Minimal uzunlikdagi daraxtni topish muammosi ko'pincha xuddi shunday sharoitda uchraydi: masalan, har qanday shahardan boshqasiga (to'g ridan-to'g ri yoki boshqa shaharlar orqali) o'tish uchun n ta shaharlarni yo'llar ʻ ʻ bilan bog lash kerak. Berilgan juft shaharlar o'rtasida yo'llar qurishga ruxsat ʻ beriladi va har bir bunday yo'lni qurish qiymati ma'lum. Qurilishning umumiy narxini minimallashtirish uchun qaysi yo'llarni qurish kerakligini hal qilish talab qilinadi. Ushbu muammoni grafika nazariyasi nuqtai nazaridan shakllantirish mumkin. Bu yerda berilgan grafnin uchlari shaharlarni, qirralari esa to'g ri yo'l ʻ qurilishi mumkin bo'lgan va qirralarning og irliklari teng bo'lgan shaharlarni ʻ ifodalaydigan minimal daraxtini topish muammosidir. Minimal uzunlikdagi daraxtni topish uchun bir nechta algoritmlar mavjud. Eng mashhurlari quyida keltirilgan: 1) Kruskal algoritmi; 2) Prima algoritmi; 3) Boruvka algoritmi; 4) Teskari o'chirish algoritmi; Quyida ushbu algoritmlarni ko rib chiqamiz ʻ 2.1 Kruskal algoritmi Kruskal algoritmida qirralarning butun birlashtirilgan ro'yxati kamaymaydigan uch darajalariga muvofiq tartiblangan. Bundan tashqari, qirralar darajalari kichikroq bo'lgan qirralardan yuqori tomonga siljiydi va keyingi uch 3
ilgari tanlangan qirralar bilan sikl hosil qilmasa, karkasga qo'shiladi. Xususan, grafdagi minimal darajadagi qirralaridan biri har doim birinchi bo'lib tanlanadi.Tanlangan qirralarning sikl hosil qilmasligini tekshirish uchun biz grafni bir nechta bog langan komponentlarning birlashishi sifatida namoyish etamiz. Engʻ boshida, grafning chekkalari tanlanmaganida, har bir uch alohida bog langan ʻ komponent hisoblanadi. Yangi qirralar qo'shilganda, ulanish komponentlari bitta umumiy ulanish komponenti bo'lguncha birlashadi. Barcha bog langan tarkibiy ʻ qismlarni raqamlaymiz va har bir uch uchun uning ulangan qismlarini sonini saqlaymiz, shuning uchun har bir uch uchun boshida uning bog langan ʻ komponentlari soni uchning o'zi soniga teng bo'ladi va oxirgi barcha uchlar bir- biriga bog langan komponentning bir xil raqamlariga tegishli bo'ladi. ʻ Keyingi qirrani ko'rib chiqayotganda, ushbu qirraning uchlariga to'g ri ʻ keladigan ulangan komponentlarning raqamlarini ko'rib chiqamiz. Agar bu raqamlar bir xil bo'lsa, unda qirra allaqachon bir xil bog langan komponentda ʻ joylashgan ikkita uchni birlashtiradi, shuning uchun bu qirrani qo'shish siklni tashkil qiladi. Agar qirra ikki xil bog langan komponentni, masalan, a va b ʻ raqamlari bilan bog lasa, u holda qirra asosiy daraxtning bir qismiga qo'shiladi va ʻ bu ikkita bog langan komponentlar birlashtiriladi. Buning uchun, masalan, ilgari ʻ komponentida bo'lgan barcha uchlar uchun komponent raqaminiga o'zgartirish kerak. Kruskal algoritmini amalga oshirish bosqichlari quyidagicha: 1) Barcha qirralarni quyidan yuqorigacha saralash. 2) Vazni eng kichik qirrasini oling va uni daraxtga qo'shing. Agar qirra qo shilganda, sikl hosil bo lsa, u holda bu qirrani olib tashlang. ʻ ʻ 3) Barcha uchlarga yetguncha qirralarni qo'shishni davom eting. 2.2 Kruskal algoritmiga kirish: Bu yerda biz berilgan vaznli grafikning MST (Minumum Spanning Tree) ni topish uchun Kruskal algoritmini muhokama qilamiz . 4
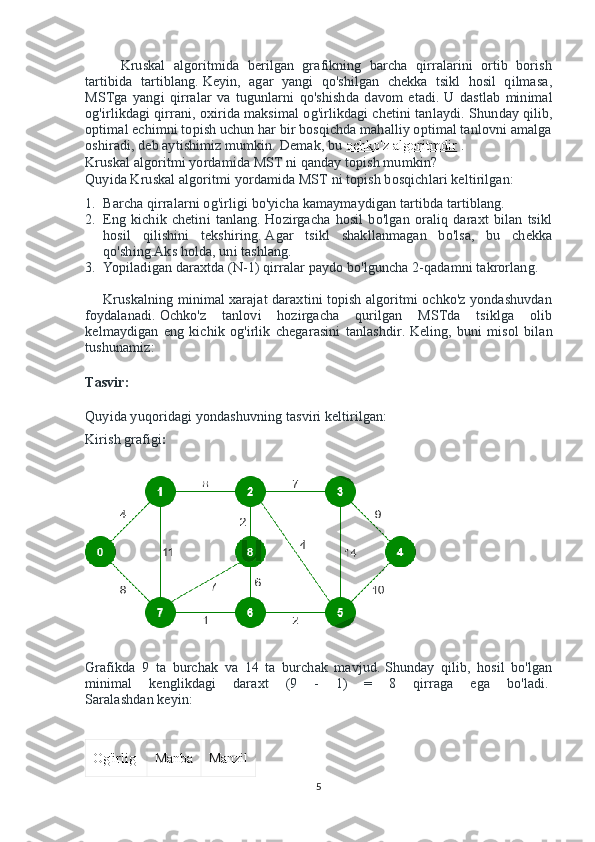
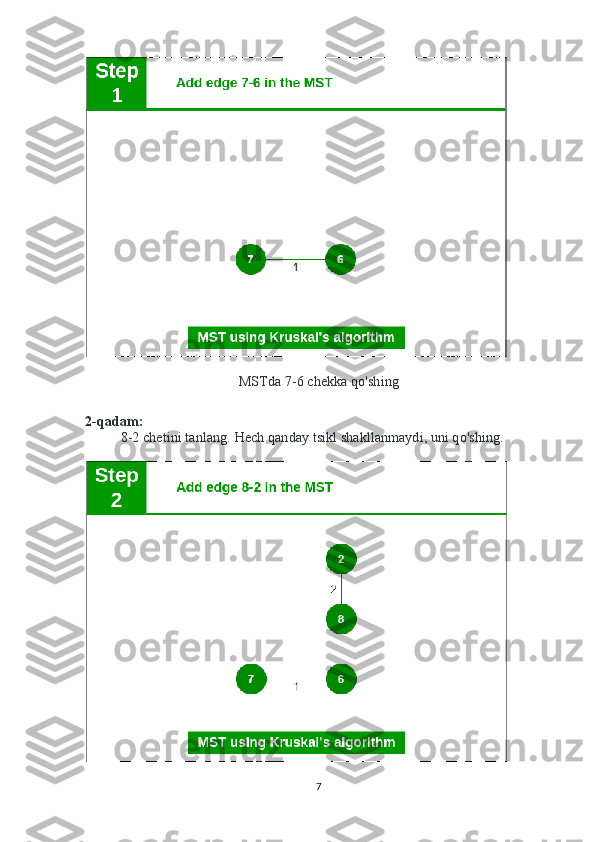
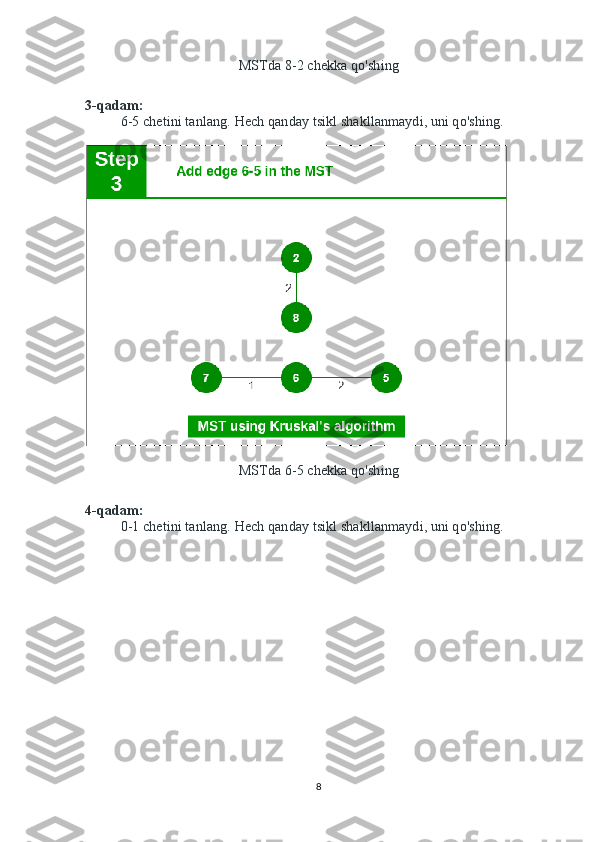
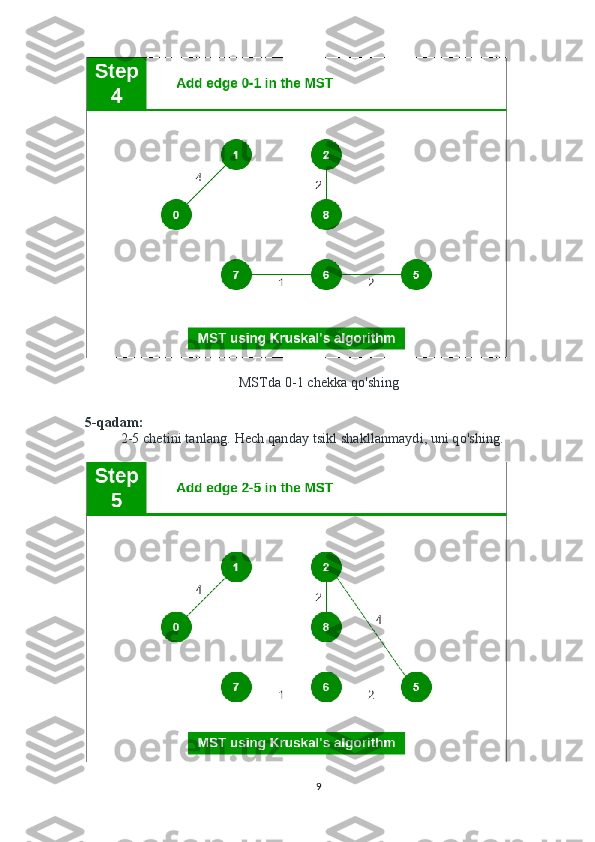
Kruskal algoritmida berilgan grafikning barcha qirralarini ortib borish tartibida tartiblang. Keyin, agar yangi qo'shilgan chekka tsikl hosil qilmasa, MSTga yangi qirralar va tugunlarni qo'shishda davom etadi. U dastlab minimal og'irlikdagi qirrani, oxirida maksimal og'irlikdagi chetini tanlaydi. Shunday qilib, optimal echimni topish uchun har bir bosqichda mahalliy optimal tanlovni amalga oshiradi, deb aytishimiz mumkin. Demak, bu ochko'z algoritmdir . Kruskal algoritmi yordamida MST ni qanday topish mumkin? Quyida Kruskal algoritmi yordamida MST ni topish bosqichlari keltirilgan: 1. Barcha qirralarni og'irligi bo'yicha kamaymaydigan tartibda tartiblang. 2. Eng kichik chetini tanlang. Hozirgacha hosil bo'lgan oraliq daraxt bilan tsikl hosil qilishini tekshiring. Agar tsikl shakllanmagan bo'lsa, bu chekka qo'shing.Aks holda, uni tashlang. 3. Yopiladigan daraxtda (N-1) qirralar paydo bo'lguncha 2-qadamni takrorlang. Kruskalning minimal xarajat daraxtini topish algoritmi ochko'z yondashuvdan foydalanadi. Ochko'z tanlovi hozirgacha qurilgan MSTda tsiklga olib kelmaydigan eng kichik og'irlik chegarasini tanlashdir. Keling, buni misol bilan tushunamiz: Tasvir: Quyida yuqoridagi yondashuvning tasviri keltirilgan: Kirish grafigi : Grafikda 9 ta burchak va 14 ta burchak mavjud. Shunday qilib, hosil bo'lgan minimal kenglikdagi daraxt (9 - 1) = 8 qirraga ega bo'ladi. Saralashdan keyin: Og'irlig Manba Manzil 5
