KOMPLEKS SONLAR VA ULAR USTIDA AMALLAR






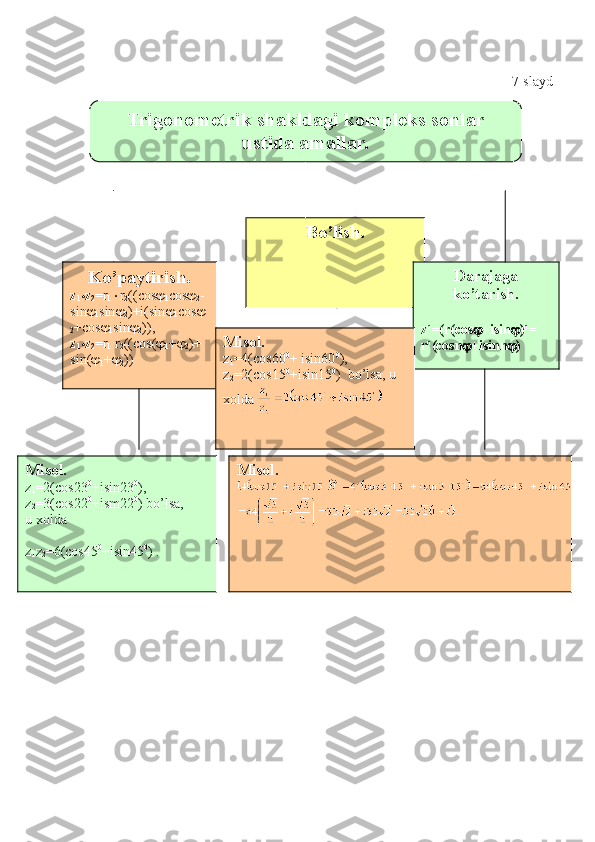
![Misol:
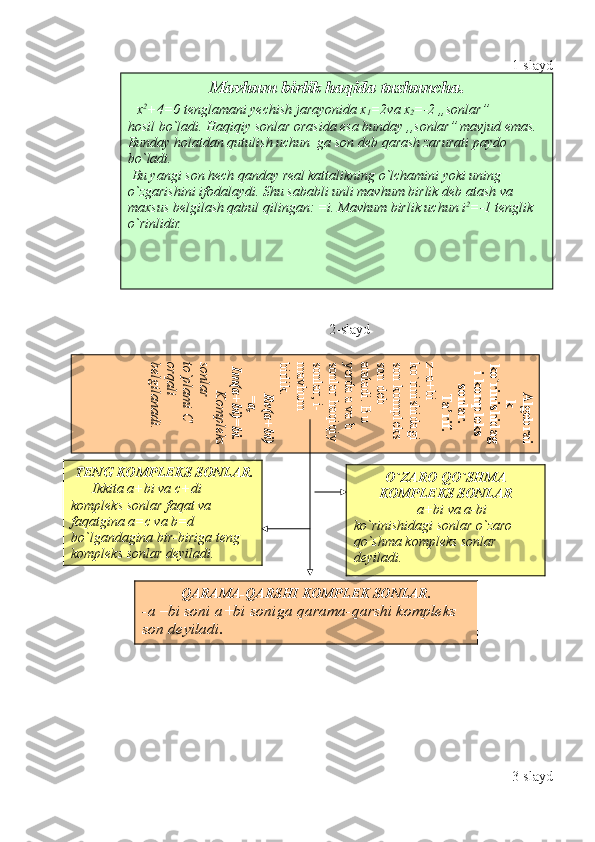
O‘rin almashtirish, gruppalash qonuni kompleks sonlarda ham to’g’ri:
(a+bi) + (c+di) = (c+di) + (a+bi)
(a+bi) · (c+di) = (c+di) · (a+bi)
(a+bi) + (c+di) + (e+fi) = (a+bi) + [(c+di) + (e+fi)]1-teorema.
Isbot . z=a + bi,w = c + 4i bo'lsin. U holda = a-bi, = c-di va =
= a + c - (b + d)i = (a - bi) + (c- di) =
2-teorema.
I s b o t. Haqiqatan,
= = ac - bd - -(ad + bc)i. Ikkinchi
tomondan,
= (a-bi)(c-di) = ac- bd-(ad+bc)i. Natijalar bir xil. Demak,
.Xususan,z 0 bo'lsa, z ga teskari bo'lgan songa qo'shma son z ga qo'shma sonning
teskarisi bo'ladi. Haqiqatan, 2- teoremaga ko'ra z = l tenglikdan = 1
olinadi. Bundan =
N a t i j a. Kompleks sonning natural ko'rsatkichli da rajasiga qo'shma son, berilgan songa
qo'shma sonning shu natural ko'rsatkichti darajasiga teng; .](/data/documents/882af0e8-dc05-4972-ad24-e446723d1882/page_7.png)

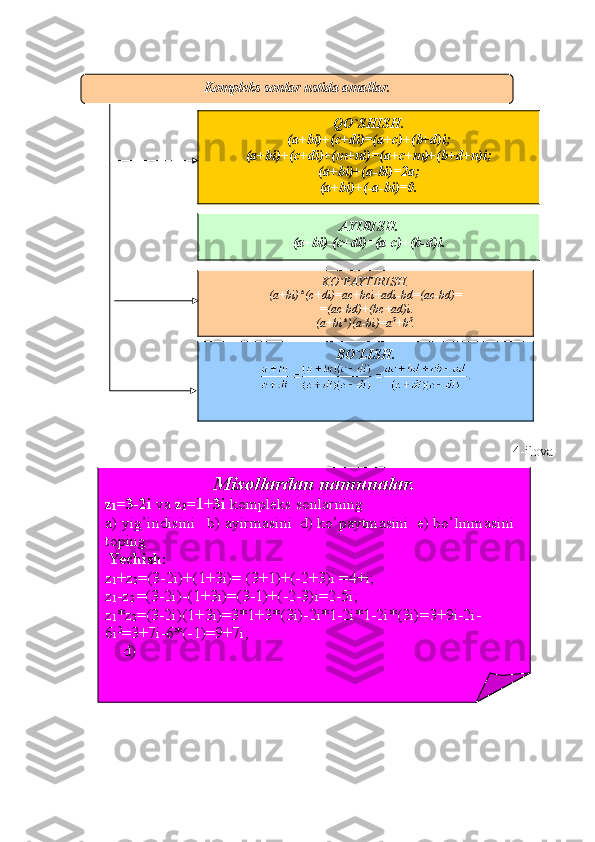
![Yuqoridagi mulohazalardan ko'rinadiki, agar Arg(z) bo'lsa, u holda ixtiyoriy k Z son
uchun + 2 k Arg(z) bo'ladi. Shu sababli Arg(z) to'plamni quyidagicha tasvirlash
mumkin:
Arg(z) = { + 2 k : k Z}.
Burish burchagining kosinusi va sinusi ta'riflaridan ko'rinadiki, z = x + yi kompleks
sonning har qanday cp argument! uchun quyidagi munosabatlar o'rinli:
cos = , sin =
Bu tengliklar asosida, z = x + yi kompleks sonini z = z|(cos( + i sin ) ko'rinishida
yozib olish mumkin. Bunday yozish kompleks sonni trigonomelrik shaklda tasvirlash deb
yuritiladi.
Kompleks son cheksiz ko'p argumentlarga ega bo'lgani uchun, uni cheksiz ko'p usullar
bilan trigonometrik shaklda yozish mumkin. Shu sababli kompleks sonning trigono metrik
shaklini tayin bir oraliqda yotadigan argument orqali yozish maqsadga muvofiqdir. Biz ana
shunday oraliq sifatida [0; 2 ] oraliqni olamiz. Bu oraliqda har qanday z(z 0 ) kompleks
sonining faqat bitta argumenti yotadi.
z = x + yi kompleks sonining [0; 2 ] oraliqda yotadi gan argumenti shu sonning bosh
argumenti deyiladi va arg(z) bilan belgilanadi. Shunga muvofiq ravishda,z = z |
(cos(arg(z)) + isin(arg(z))) ni z kompleks sonning bosh trigonometrik shakli deb ataymiz.
Bundan keyin, kompleks sonning argumenti va kompleks sonning trigo nometrik shakli
deyilganda, mos ravishda kompleks son ning bosh argumenti va bosh trigonometrik shakli
nazarda tutiladi.
Endi z = 0 soni ustida to'xtalamiz. Bu sonning moduli 0 ga teng, lekin argumenti
aniqlanmaydi.](/data/documents/882af0e8-dc05-4972-ad24-e446723d1882/page_9.png)






“ KOMPLEKS SONLAR VA ULAR USTIDA AMALLAR ” M U N D A R IJA Kirish . I BOB. Algebraik shakldagi kompleks sonlar va ular ustida amallar . 1.1 Qo’shish amali. 1.2 Ayirish amali. 1.3 Ko‘paytirish amali. 1.4 Bo‘lish amali. II BOB. . Trigonometrik shakldagi kompleks sonlar va ular ustida amallar. III BOB. Tr i gonometrik shaklda berilgan kompleks sonlarni ko’paytirish, bo’lish,darajaga ko’tarish. IV BOB. Kompleks sondan ildiz chiqarish. V BOB. Prеzеntatsiya namoyishlar Xulosa Foydalanilgan adabiyotlar
Samarqand Davlat Universiteti xuzuridagi pedagog kadirlarni qayta tayyorlash va ularni malakasini oshirish mintaqaviy markazining “Matematika” fani o’qituvchisi Babakulova Dilbarningning “Kompleks sonlar va ular ustida amallar” ” Mavzusidagi Bitiruv ishiga ilmiy raxbarning X U L O S A S I Bugungi kunda ta’lim jarayonida matematika ga bo’lgan talab borgan sari ortib bormoqda. Fan ta’lim rivojlangan sari Axborot texnologiyalarining ham yangidan yangi turlari ko’plab imkoniyatlari yaratilmoqda. Axborot texnologiyalari nafaqat ta’lim tizimida balki barcha sohalarda ham qo’llanilib kelinmoqda. Xozirgi vaqtda biror bir sohani matematikasiz tasavvur qilish qiyin. Ushbu Bitiruv Malakaviy Ishida Komplek sonlar va ular ustida amallarini misol va masalalar bilan yoritib berilgan. Shu bilan birga slaytlar bilan yanada to’liq yoritib bera olgan . Babakulova Dilbar tomonidan tayyorlangan “Komplek sonlar va ular ustida amallar” mavzusidagi Bitiruv ishi o’rnatilgan talablarga mos ravishda tayyorlangan va talab qoidalarga to’liq mos keladi. Mavzuni o’rganuvchi uchun oson qilib yoritib bergan. Ushbu Bitiruv Malakaviy ishini ijobiy tomondan baholash mumkin deb xisoblayman. Ilmiy Raxbar: N.Ravshanova
KIRISH Mavzuning dolzarbligi. Mustaqillikka erishilgandan keyin barcha sohalardagi kabi ta`lim tizimida ham jiddiy islohatlar amalga oshirildi, ta`limning sifatini yaxshilashga kirishildi. Ta`lim berishning yangi usullari joriy qilina boshlandi. Shulardan eng asosiysi o`quvchilarga yangi pedagogik texnologiya asosida dars berish masalasi. Bu usulni matematika sohasida ishlashga ham tadbiq qilish yangi samara berishi amalda tasdiqlandi. O`quvchilarning badiiy didini o`stirish, dunyoqarashini kengaytirish uchun ularning kompyuter va zamonaviy tehnalogiyalar asosida ishlashi juda muhim. Buning usullarini ishlab chiqish esa, hech qachon dolzarbligini yo`qotmaydi. Biz mazkur bitiruv ishimizda bu xususida o`z taklif va mulohazalarimizni ifodalashga harakat qilamiz. Jamiyatning barcha qatlamlarini, ayniqsa, yoshlarni yuksak ma`naviyat va ma`rifat sohibi qilib tarbiyalash bugungi kunning dolzarb masalasidir. Kursni tugatish ishining maqsadi. Bitiruv makalaviy ishimizni yozishdan asosiy maqsadi o’quvchilarga o’z sohamiz bo’yicha to’g’ri tarbiya berish bilan birga Kompleks sonlar va ular ustida amallarni o’rgatish usullarining eng qulay va sodda tartibda o’rgatish yo’llari haqida bayon qilamiz. Kursni tugatish ishining obyekti. Kasb-hunar maktabi o’quvchilari va pedagoglar. Mazkur kurs ishi kompleks sonlar va ular ustida amallar oid manbalar va uslubiy tavsiyalarni o`z ichiga oladi.
I BOB. 1. Algebraik shakldagi kompleks sonlar va ular ustida amallar . Kompleks sonlar ta'limoti ilm-u fanda, xususan, ma tematikada alohida o'rin tutadi. Tez rivojlanayotgan bu soha texnikada, shuningdek ishlab chiqarishning ko'plab so halarida g'oyat keng qo'llanishga ega. Shu sonlar haqida ayrim ma'lumotlarni keltiramiz. Xususiy bir misoldan boshlaylik. x 2 + 4 = 0 tenglamani yechish jarayonida x 1 = 2 va x 2 = -2 «sonlar» hosil bo'ladi. Haqiqiy sonlar orasida esa bunday «sonlar» mavjud emas. Sunday holatdan qutulish uchun ga son deb qarash zarurati paydo bo'ladi. Bu yangi son hech qanday real kattalikning o'lchamini yoki uning o'zgarishini ifodalamaydi. Shu sababli uni mavhum (xayoliy, haqiqatda mavjud bo'lmagan) birlik deb atash va maxsus belgilash qabul qilingan: = i. Mavhum birlik uchun i 2 =-l tenglik o'rinlidir. a + bi ko'rinishdagi ifodani qaraymiz. Bu yerda a va b lar istalgan haqiqiy sonlar, i esa mavhum birlik. a + bi ifoda haqiqiy son a va mavhum son bi lar «kompleksi»dan iborat bo'lgani uchun uni kompleks son deb atash qabul qilingan. a + bi ifoda algebraik shakldagi kompleks son deb ataladi, bu yerda a R, b R, i 2 = - 1. Bu paragrafda a + bi ni qisqalik uchun «algebraik shakldagi kompleks son» deyish o'rniga «kompleks son» deb ishlataveramiz. Kompleks sonlarni bitta harf bilan belgilash qulay. Masalan, a + bi ni z = a + bi ko'rinishda belgilash mumkin.z =a + bi kompleks sonning haqiqiy qismi a ni Re(z) (fransuzcha reele - haqiqiy) bilan, mavhum qismi b ni esa Im(z)(fransuzcha imaginaire — mavhum) bilan belgilash qabul qilingan: a= Re(z), b = Im(z). Agar z=a + bi kompleks son uchun b=0 bo'lsa, haqiqiy son z = a hosil bo'ladi. Demak, haqiqiy sonlar to'plami R barcha kompleks sonlar to'plami C ning qism to'plami bo'ladi R C. 1 - m i s o l . z 1 = l+2i, z 2 = 2-i, z 3 = 2 , 1 , z 4 = 2i, z 5 = 0 kompleks sonlarning haqiqiy va mavhum qismlarini topamiz. Yechish. Kompleks son haqiqiy va mavhum qismlarining aniqlanishiga ko'ra, quyidagilarga egamiz: Re(z 1 )=l; Re(z 2 ) = 2; Re(z 3 ) = 2,l; Re(z 4 ) = 0; Re(z s )=0; Im(z 1 )=2; Im(z 2 ) = -i; Im(z 3 ) = 0; Im(z 4 ) = 2i; Im(z s ) = 0. Kompleks sonlar uchun « < », « > » munosabatlari aniqlanmaydi, lekin teng kompleks sonlar tushunchasi kiritiladi. Haqiqiy va mavhum qismlari mos ravishda teng bo'lgan kompleks sonlar teng kompleks sonlar deb ataladi. Masalan, z, = 1 , 5 + va z 2 = + 0,8i sonlari uchun Re(z 1 ) = Re(z 2 ) = l,5, Im(z 1 ) = Im(z 2 ) = 0,8. Demak, z 1 = z 2 Bir-biridan faqat mavhum qismlarining ishorasi bilan farq qiladigan ikki kompleks son o'zaro qo'shma kompleks son lar deyiladi. z =a+ bi kompleks songa qo'shma kompleks son = a-bi ko'rinishda yoziladi. Masajan, 6+ 7i va 6- 7i lar qo'shma kompleks sonlardir: = 6-7i. Shu kabi soniga qo'shma son = z bo'ladi. Masalan, = =6+7i. a haqiqiy songa qo'shma son a ning o'ziga teng: = = a - 0 i =a. Lekin bi mavhum songa qo'shma son =-bi dir. Chunki = =0-bi=-bi,
a , b R. . Kompleks sonlar ustida arifmetik amallar quyidagicha aniqlanadi: (a + bi ) + (c + di ) = (a + c) + (b + d )i; (1) (a + bi) - (c + di) = (a - c) + (b- d )i; (2) (a + b i ) ( c + di ) = (ac - bd ) + (ad + bc)i (3) (4) (1) va (2) tengliklarni bevosita qo'llash qiyin emas. Kompleks sonlarni ko'paytirish amalini i 2 = -1 ekanligini e'tiborga olib, ko'phadlarni ko'paytirish kabi bajarish mumkin. 2 - m i s o l . ( 2 - i ) ( + 2 i ) = 2 + 2 2 i - i - 2 i 2 = + 4 i - i + 2 = + i . (4) formulani eslab qolish va amaliyotda bevosita qo'l lash ancha qiyin. Shu sababli ni hisoblash uchun, uning surati va maxrajini c - di ga ko'paytirib, tegishli amal larni bajarish qulaydir. 3-misol . Kompleks sonlarni qo'shish va ko'paytirish amallari xossalari haqiqiy sonlarnikiga o'xshash; 1) z + w= w + z; 1') zw = wz; 2) (z + w) + t = z+(w + t); 2 ' ) (zw)t=z(wt); 3) z + 0= z; 3' ) z l = z ; 4) z(w +t) = zw +zt. z +w = 0 tenglikni qanoatlantiruvchi z, w kompleks sonlari o'zaro qarama-qarshi sonlar deyiladi. z kompleks soniga qarama-qarshi sonni -z bilan belgilash qabul qilingan. z = a + bi kompleks songa qarama-qarshi bo'lgan yagona kompleks son mavjud va bu son – z=-a- bi komp leks sonidan iborat. zw=1 tenglikni qanoatlantiradigan z va w kompleks sonlari o'zaro teskari kompleks sonlar deyiladi. z = 0 soniga teskari son mavjud emas. Har qanday z 0 kompleks songa teskari kompleks son mavjud. Bu son - sonidan iborat. z = a + bi kompleks songa teskari bo'lgan sonini topamiz: bunda i 2 har safar -1 ga almashtiriladi.
