Matlab modellashtirish muhitida dasturlash asoslari.


![1 . Arifmetik amallar.
Matlabda skalyar miqdorlar ustida quyidagi oddiy arifmyetik amallarni
bajarish mumkin:
+ - qo’shish;
- - ayirish;
* - ko’paytirish;
/ - o’ngdan bo’lish;
\ - chapdan bo’lish;
^ - darajaga oshirish.
Agar bir qatordagi ifodada bir nyechta amallar bo’lsa, ularni bajarilish
kyetma-kyetligi quyidagi ustivorlik qoidasi bo’yicha amalga oshiriladi:
Matlabda bu qoidalar skalyar miqdorlarga oddiy usulda qo’llaniladi.
Masalan,
2. Vektorlar va matritsalar ustida amallar.
Arifmetik amallarni matritsalar ustida ham bajarish mumkin, faqat ularni bajarish
qoidalari skalyar miqdorlarnikidan farqli bo’ladi. Qo’shish va ayirish amallari
matritsalar uchun ularning mos elyemyentlari orasida bajariladi. Shuning uchun a
va b matritsalarni qo’shish va ayirish uchun ularning o’lchovlari bir xil bo’lishi
talab etiladi: a va b (nxm) o’lchovli bo’lsa, u holda
s = a±b
Matritsa elyemyentlari s[i,j]=a[i,j]+b[i,j] tyengliklar bilan aniqlanadi. Masalan,
a=[ 1 2 3; 4 5 6] ,
b=[4 5 3; 2 3 -4],
c=a+b,
c=[5 7 6; 6 8 2] ,](/data/documents/07c3033b-29e8-4483-a5af-696d1bd56081/page_3.png)
![d=a-b,
d=[-3 -3 0; 2 2 10].
a va b matritsalar o’lchovlari har xil bo’lsa, ular ustida qo’shish va ayirishni
bajarib bo’lmaydi.
Matritsalarni ko’paytirish esa xuddi algyebradagi qoida bo’yicha bajariladi. Bu
holda chapdagi matritsaning ustunlari soni o’ngdagi matritsaning qatorlari soniga
tyeng bo’lishi kyerak: a ning o’lchovi (mxk) b niki (kxm) bo’lsa, u holda c=a+b
matritsa (nxm) o’lchovli bo’ladi:
i=1,n , j=1,m.
Masalan:
a=[ 1 2
0 3
2 2 ] b= [
0
1
1 2 3
0 2 3]
bo’lsa, c=a*b quyidagicha bo’ladi.
C=
[ 2 1
3 0
2 2 6 9
6 9
8 12 ]
Agar skalyar miqdor matritsaga ko’paytirilayotgan bo’lsa, u matritsaning har
bir elementiga ko’paytiriladi:
d=3*b bo’lsa, d=
[ 0
3 3 6 9
0 6 9 ] ga teng bo’ladi.
Misol: x=[2 1; 0 3; 2 3] , y=[1 2 3 4; 2 -1 3 1] matritsalarda x*y amalni
qo’lda va kompyuterda bajarib, natijalarni solishtiring.
Undan tashqari, matlabda matritsalarni mos elementlari orasida bajariladigan
quyidagi amallar mavjud. Bu amallarni boshqalardan ajratish uchun belgi oldiga (.)
nuqta qo’yiladi.](/data/documents/07c3033b-29e8-4483-a5af-696d1bd56081/page_4.png)
![a.*b- a ning har bir elementi b ning mos elementiga ko’paytiriladi;
a./b- a ning har bir elementi b ning mos elementiga bo’linadi;
a.\b- b ning har bir elementi a ning mos elementiga bo’linadi;
a.^b- a ning har bir elementini b ning mos elementi darajasiga oshiriladi.
Masalan, a=[1 2 3; 2 3 1], b=[0 1 2; 2 1 2] bo’lsa , u holda c=a.*b
quyidagicha bo’ladi:
c=[0 2 6; 4 3 2].
c matritsadan (:) komandasi yordamida c1(1,:), c2(2,:) qator- vektorlarni
hosil qilamiz va c2ni transponerlab quyidagicha
c1*c2’=18
amalga oshirilgan ko’paytmani c1 va c2 vektorlarning (ichki) skalyar
ko’paytmasi deyiladi.
c1’*c2
ko’paytma esa (3x3) o’lchovli matritsa bo’ladi. Bu ko’paytma tashqi
ko’paytma deyiladi.
3.Solishtirish va mantiqiy amallar.
Mantiqiy amallarni ikki guruhga bo’lib o’rganamiz:
a)solishtirish amallari;
b)haqiqiy mantiqiy amallar.
Solishtirish amallariga quyidagilar kiradi:
a>b- katta amali;
a<b- kichik amali;
a<=b- kichik yoki teng amali;
a>=b- katta yoki teng amali;
a==b- teng amali;
a~=b-teng emas amali.
Massivlarni solishtirishda bu amallar ularning mos elementlari orasida
amalga oshiriladi. Bunda solishtirilayotgan massiv o’lchoviga teng o’lchovli
massiv xosil bo’ladi. Ya’ni massivning mos elementi 1 bo’ladi, agar solishtirish](/data/documents/07c3033b-29e8-4483-a5af-696d1bd56081/page_5.png)
![natijasi “rost” bo’lsa , 0 bo’ladi agar solishtirish natijasi “yolg’on” bo’lsa. Agar
solishtirishda >, <, >=, <= amallari ishlatilsa elementlarning faqat haqiqiy qismi
solishtiriladi, == yoki ~= amallari ishlatilsa elementlarning ham haqiqiy, ham
mavhum qismlari solishtiriladi.
Ikkita qatorni ekvevalentligini tekshirish uchun strcmp komandasdan
foydalaniladi. Bu holda vektorlarning uzunliklari har xil bo’lishi mumkin.
Agar solishtirilayotganlardan biri skalyar, ikkinchisi matritsa bo’lsa, u holda
solishtrish uchun skalyarni matritsa o’lchovlariga teng qilib, matritsaga to’ldiriladi
va undan keyin solishtiriladi. Masalan:
a=3;
b=[1 4 0; 2 5 7];
bo’lsa a>b natijasi quyidagicha bo’ladi:
ans=[1 0 1; 1 0 0]
Matritsa elementlari kompleks bo’lgan holda misol ko’ramiz:
c=[5+2i 4-i];
d=[5+7i 3-i];
d<=c ning natijasi
ans=1 1,
c<=d ning natijasi
ans= 1 0
bo’ladi.
Matlabda haqiqiy mantiqiy amallarga quyidagilar kiradi:
&=”va” amali;
|-“yoki” amali;
~-“yo’q” amali.
Mantiqiy amallar matritsalarni mos elemntlari orasida bajariladi. Bu
amllarni bajarishda 0 ishlatiladi, agar amal natijasi “yolg’on” bo’lsa va “rostlik”ni
bildiruvchi mantiqiy bir ixtiyoriy nol bo’lmagan son bo’lishi mumkin.](/data/documents/07c3033b-29e8-4483-a5af-696d1bd56081/page_6.png)

![4) [x,w]=isqnonneg(…)-yechim bilan birga qoldiqlar vektori kvadrati ikkinchi
normasini qaytaradi;
5) [x,w,w1]=isqnonneg(…)-xuddi avvalgi buyruq kabi, yana qoldiqlar vektori w1
ni qaytaradi;
6) bicg(A,B)-Ax=B ning x yechimini qaytaradi; A(nxn), B(nx1). Bunda hisoblash
iteratsiyalar yaqinlashguncha yoki min{20,n} gacha bajariladi;
7) bisc(A,B,tol)-yechimni tol xatolik bilan qaytaradi;
8) bisc(A,B,tol,maxit)-avvalgi buyruq kabi, yechimni undan tashqari maxit-
maksimal iteratsiyalar soni bilan qaytaradi.
4.Tayinlash va shartli operatori.
Ulardan biri shartli o’tish operatori if ning formatlari bilan tanishib
chiqamiz. Umumiy holda if operatorining formati:
if <1-shart>
{ operator1}
elseif <2-shart>
{ operator2}
else
{ operator3}
end
ko’rinishida bo’ladi. Agar 1-shart “rost” bo’lsa, boshqarish {operator1}ni
bajarishga uzatiladi. Aks holda, ya’ni 1-shart “yolg’on” bo’lsa, u holda boshqarish
2-shartni tekshirishga uzatiladi. Agar y “rost” bo’lsa boshqarish {operator2}ni
bajarishga uzatiladi, aks holda boshqarish {operator3}ni bajarishga uzatiladi.
Yuqoridagi formatda shartlar sifatida algebraik ifodalar, mantiqiy va
solishtirish amallari bo’lgan >=, <=, <, >, ~=, == kabilar ishlatilishi mumkin.
Masalan,
if i==j
a(i,j)=i+j+2;
elseif abs(i-j)==1](/data/documents/07c3033b-29e8-4483-a5af-696d1bd56081/page_8.png)

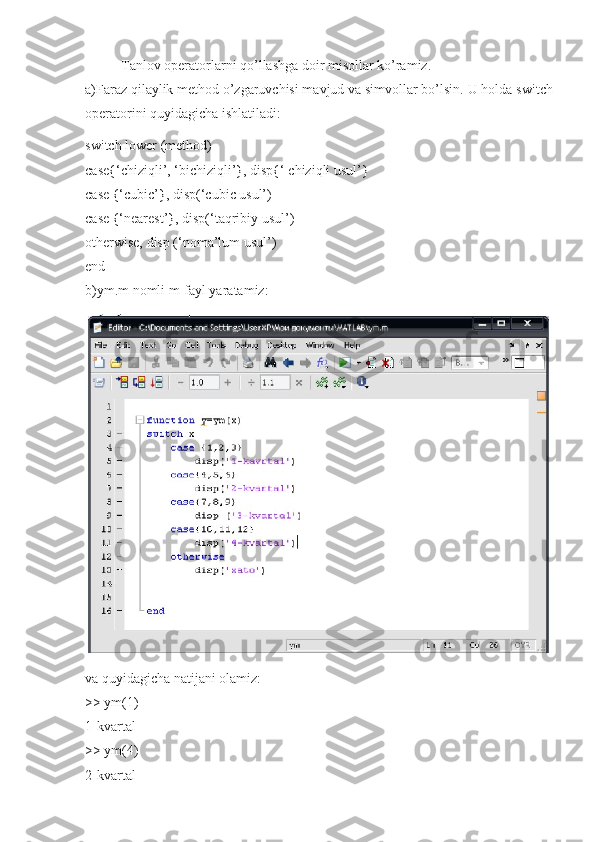


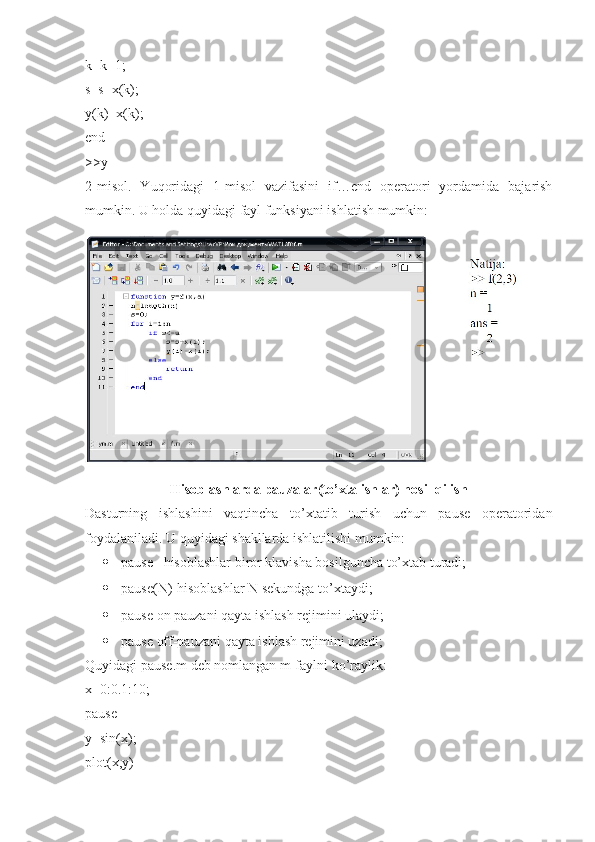


Mavzu: Matlab modellashtirish muhitida dasturlash asoslari. Reja: I. Kirish II. Asosiy qism 1. Arifmetik amallar . 2. Vektorlar va matritsalar ustida amallar . 3. Solishtirish va mantiqiy amallar . 4. Tayinlash va shartli operatori. 5. Sikl operatorlari . 6. Tanlash operatorlari . 7. Dasturlashga doir misollar. Hisoblashlarda to’xtashlar hosil qilish. 8. Foydalanilgan adabiyotlar.
Kirish. Dasturlash MATLAB tizimida uning imkoniyatlarini kengaytirishi mumkin. Uning foydalanish imkoniyatlarini yanada oshiradi. Yuqorida dasturlashning ma’lum elementlari bilan tanishdik. Bu yerda MATLAB tilining to’ldiruvchi qoidalarini ko’rib o’tamiz. Dasturlash tilida konstantalar va o’zgaruvchilar ishlatiladi. O’zgaruvchi bu ob’ekt nomlariga ega bo’lib, o’zida turli ma’lumot qiymatlarini saqlash xususiyatiga ega. O’zgaruvchining bu ma’lumot qiymatlari sonlar yoki simvollar, vektorlar yoki matritsalar bo’lishi mumkin. O’zgaruvchining aniq bir qiymatini berish uchun o’zlashtirish operatori ishlatiladi: Uning umumiy ko’rinishi quyidagicha: O’zgaruvchi_nomi = ifoda; O’zgaruvchining tipi oldindan e’lon qilinmasligi mumkin. Ular o’zgaruvchining o’zlashtirayotgan ifoda qiymatiga qarab aniqlanadi. O’zgaruvchining nomi bir nechta simvollardan tashkil topishi mumkin, lekin boshlang’ich 31 ta simvol identifikatsiya qilinadi. O’zgaruvchining nomi harf bilan boshlanadi. Bundan tashqari harf, raqam, simvol va ostiga chiziqlar bo’lishi mumkin. Nomda probel va maxsus belgilar ishlatish mumkin emas. Matematik ifodalarda monitor ekraniga joylashmagan holda uning ma’lum qismini keyingi qatorga ko’chirish maqsadga muvofiq. Buning uchun ko’p nuqta (…) simvoli ishlatiladi. Buyruq rejimida bitta satrdagi simvollar soni 4096 ta bo’lishi mumkin. M-faylda esa cheklanmagan, lekin bunday uzun satrlar bilan ishlash noqulay. Shuning uchun satrdagi simvollarni ko’chirish dasturni sifatini yaxshilaydi.
1 . Arifmetik amallar. Matlabda skalyar miqdorlar ustida quyidagi oddiy arifmyetik amallarni bajarish mumkin: + - qo’shish; - - ayirish; * - ko’paytirish; / - o’ngdan bo’lish; \ - chapdan bo’lish; ^ - darajaga oshirish. Agar bir qatordagi ifodada bir nyechta amallar bo’lsa, ularni bajarilish kyetma-kyetligi quyidagi ustivorlik qoidasi bo’yicha amalga oshiriladi: Matlabda bu qoidalar skalyar miqdorlarga oddiy usulda qo’llaniladi. Masalan, 2. Vektorlar va matritsalar ustida amallar. Arifmetik amallarni matritsalar ustida ham bajarish mumkin, faqat ularni bajarish qoidalari skalyar miqdorlarnikidan farqli bo’ladi. Qo’shish va ayirish amallari matritsalar uchun ularning mos elyemyentlari orasida bajariladi. Shuning uchun a va b matritsalarni qo’shish va ayirish uchun ularning o’lchovlari bir xil bo’lishi talab etiladi: a va b (nxm) o’lchovli bo’lsa, u holda s = a±b Matritsa elyemyentlari s[i,j]=a[i,j]+b[i,j] tyengliklar bilan aniqlanadi. Masalan, a=[ 1 2 3; 4 5 6] , b=[4 5 3; 2 3 -4], c=a+b, c=[5 7 6; 6 8 2] ,
d=a-b, d=[-3 -3 0; 2 2 10]. a va b matritsalar o’lchovlari har xil bo’lsa, ular ustida qo’shish va ayirishni bajarib bo’lmaydi. Matritsalarni ko’paytirish esa xuddi algyebradagi qoida bo’yicha bajariladi. Bu holda chapdagi matritsaning ustunlari soni o’ngdagi matritsaning qatorlari soniga tyeng bo’lishi kyerak: a ning o’lchovi (mxk) b niki (kxm) bo’lsa, u holda c=a+b matritsa (nxm) o’lchovli bo’ladi: i=1,n , j=1,m. Masalan: a=[ 1 2 0 3 2 2 ] b= [ 0 1 1 2 3 0 2 3] bo’lsa, c=a*b quyidagicha bo’ladi. C= [ 2 1 3 0 2 2 6 9 6 9 8 12 ] Agar skalyar miqdor matritsaga ko’paytirilayotgan bo’lsa, u matritsaning har bir elementiga ko’paytiriladi: d=3*b bo’lsa, d= [ 0 3 3 6 9 0 6 9 ] ga teng bo’ladi. Misol: x=[2 1; 0 3; 2 3] , y=[1 2 3 4; 2 -1 3 1] matritsalarda x*y amalni qo’lda va kompyuterda bajarib, natijalarni solishtiring. Undan tashqari, matlabda matritsalarni mos elementlari orasida bajariladigan quyidagi amallar mavjud. Bu amallarni boshqalardan ajratish uchun belgi oldiga (.) nuqta qo’yiladi.
a.*b- a ning har bir elementi b ning mos elementiga ko’paytiriladi; a./b- a ning har bir elementi b ning mos elementiga bo’linadi; a.\b- b ning har bir elementi a ning mos elementiga bo’linadi; a.^b- a ning har bir elementini b ning mos elementi darajasiga oshiriladi. Masalan, a=[1 2 3; 2 3 1], b=[0 1 2; 2 1 2] bo’lsa , u holda c=a.*b quyidagicha bo’ladi: c=[0 2 6; 4 3 2]. c matritsadan (:) komandasi yordamida c1(1,:), c2(2,:) qator- vektorlarni hosil qilamiz va c2ni transponerlab quyidagicha c1*c2’=18 amalga oshirilgan ko’paytmani c1 va c2 vektorlarning (ichki) skalyar ko’paytmasi deyiladi. c1’*c2 ko’paytma esa (3x3) o’lchovli matritsa bo’ladi. Bu ko’paytma tashqi ko’paytma deyiladi. 3.Solishtirish va mantiqiy amallar. Mantiqiy amallarni ikki guruhga bo’lib o’rganamiz: a)solishtirish amallari; b)haqiqiy mantiqiy amallar. Solishtirish amallariga quyidagilar kiradi: a>b- katta amali; a<b- kichik amali; a<=b- kichik yoki teng amali; a>=b- katta yoki teng amali; a==b- teng amali; a~=b-teng emas amali. Massivlarni solishtirishda bu amallar ularning mos elementlari orasida amalga oshiriladi. Bunda solishtirilayotgan massiv o’lchoviga teng o’lchovli massiv xosil bo’ladi. Ya’ni massivning mos elementi 1 bo’ladi, agar solishtirish
