PLASTIKLIK SHARTLARIDA HOLAT TENGLAMALARI

![1. Mizes-Genka plastiklik shartida holat tenglamasi
Muvozanat tenglamasi (2.2.1) va Mizes-Genka (2.2.5) plastiklik shartlari
kuchlanishlarning uchta σx,σy,τxy komponentasini o‘zida ifodalaydi. Ushbu
sistema plastiklik muvozanati holati uchun (2.2.4,a) va (2.2.5,b) kuchlanish
komponentalarini ko‘chish tezliklaridan bog‘liq bo‘lmagan hollarda ham yechish
mumkin.
Ushbu qaralayotgan masala tekis kuchlanganlik holatida sirt kuchlanishlari
uchun statik aniq hisoblanadi.
Agar
τi= τT=
σT
√3 tenglik bajarilganda bosh kuchlanishlar (2.1.6) formulalar
bilan aniqlanadi deb qabul qilsak, Mizes-Genka plastiklik sharti (2.2.5,b)
ko‘rinishda bajariladi, deb qabul qilishimiz mumkin bo‘ladi. Ushbu
τi=
σT
√3 shart
bajarilganda (2.1.7) ifodalarni hisobga olib (4.2.1) differensial tenglamalarni ba’zi
almashtirishlardan keyin quyidagicha yozish mumkin:
(√3sin ω− cos ω⋅cos 2α)∂ω
∂x
− cos ω sin 2α∂ω
∂y
+2sin ω(sin 2α∂α
∂x
− cos 2α ∂α
∂ y)= 0;
( 4.1.1)
cos ω⋅sin 2α∂ω
∂x
− (√3sin ω +cos ω⋅cos 2α)∂ω
∂y
− +2sin ω (cos 2α∂α
∂x
+sin 2α∂α
∂y)= 0.
Shunday qilib, qaralayotgan sistema tekis kuchlanganlik holati uchun ikkita
noma’lum funksiya
ω (x,y) va α(x,y) dan bog‘liq ikkita differensial tenglamalar
sistemasiga kelmoqda. Ushbu tenglamalar sistemasi yechimi shu yechimlarning
qanday turga mosligini (giperbola, parabola, ellips) xarakterlaydi.
Ushbu sistemalar tipini aniqlash uchun bir nechta chiziqlarni
L[x(S), y(S)]
bog‘liq bo‘lgan funksiyalar
α(S) va ω (S) larni qarab chiqamiz. Integral sirti
orqali o‘tgan L ni quyidagicha yozamiz:
∂α
∂x
dx + ∂α
∂ y
dy = dα ; ∂ω
∂x
dx +∂ω
∂ y
dy = dω
. (4.1.2)
Egri chiziqli urinma integrali sirtidagi L xususiy hollarda quyidagicha bo‘ladi;
∂α
∂x
; ∂α
∂y
; ∂ω
∂x
; ∂ω
∂y
.
Hosil qilingan (4.1.1) va (4.1.2) tenglamalarni L orqali chiziqli algebraik
tenglamalar ko‘rinishida yozish mumkin.](/data/documents/a6911912-4c3a-40a9-b0bf-d37f9ccc557f/page_2.png)


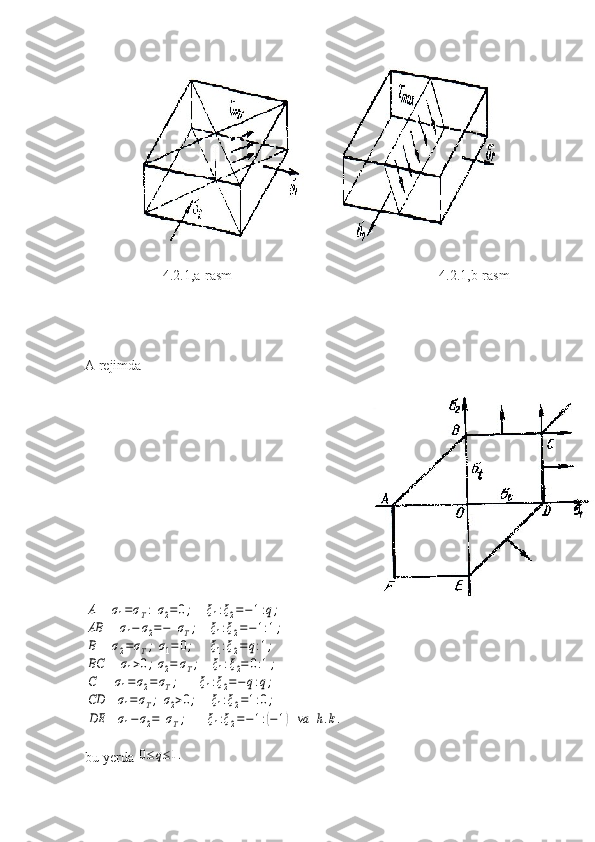
![Quyidagi holatni qarab chiqamiz, σ1σ2<0 ya’ni, bosh kuchlanish turli xil
ishoraga ega. Ushbu holatga AB va DE tartibi mos keladi DE tartib uchun
σ1>0; σ2<0; σ1−σ2=σT.
Bundan ξ1= λ¿; ξ2=− λ¿ ya’ni ξ1=−ξ2. Siqilmaslik
shartidan
ξ0=0. 4.2.2-rasm.
Tenglamalar sistemasi kuchlanishlar uchun
∂σx
∂x +
∂τxy
∂y = 0;
∂τyx
∂x +
∂σy
∂ y = 0; σ1− σ2= (σx− σy)2+4τxy
2= σT
2,
Deformatsiya tezliklari uchun,
∂σx
∂x −
∂vy
∂ y
∂vx
∂ y+
∂vy
∂x
=
σy− σx
2τyx
;
∂vx
∂x +
∂σy
∂y = 0,
(4.2.3)
Xuddi shunday AB rejim uchun ham shu ketma-ketlikda natijalar chiqariladi.
Quyidagi holatni qarab chiqamiz,
σ1⋅σ2>0 ya’ni, bosh kuchlanishlar
ishoralari bir xil. Ushbu holatga oltiburchakning BC, CD, EF, FA, rejimlari mos
keladi. (oltiburchakning vertical va gorizontal chiziqlari). CD rejim uchun
σ1>0; σ2>0; σ1=σT.
Bundan ξ1=λ¿, ξ2=0. Siqilmaslik shartidan ξ3=− ξ1. BC
rejim uchun
σ2=σT; ξ1=0; ξ2= λ¿; ξ3=ξ2. Tresk-Sen-Venan plastiklik sharti
(2.24) ni qulayroq ko‘rinishda yozamiz
σ1− σ2= 2σY−σT|σ1+σ2|
agar σ1≥ σ2 (4.2.4)
CD rejim uchun
σ1= σT. Plastiklik shartidan quyidagi shartni qanoatlantiramiz:
σ1= σ2=2σTX
, u holda
σ1+σ2= 2σT(1− X )P (4.2.5)
bu yerda
X= X(x:y)− noma’lum funksiya. Ushbu (4.2.5) shartni hisobga olib tekis
kuchlanganlik holati uchun tenzor komponentalari kuchlanishlarini quyidagicha
yozamiz [6, 7].
σx=σT[P(1− X)+X cos 2α];
σy=σT[P(1− X)− X cos 2α];
τxy=σTXsin 2α.
(4.2.6)
Bu yerda
α(x,y)− bosh kuchlanish bilan x o‘qi orasidagi burchak bo‘lib
quyidagicha aniqlanishi kerak:
P= sign σ1= sign σ2 .
Differensial tenglama muvozanati sharti (2.2.1) da (4.2.6) ni hisobga olsak,](/data/documents/a6911912-4c3a-40a9-b0bf-d37f9ccc557f/page_6.png)
![sin 2α∂α
∂x−(P+cos 2α)∂α
∂y=0;
sin 2α∂ln X
∂x −(P+cos 2α)∂ln X
∂y +2P∂x
∂y= 0.(4.2.7)
α(x;y)
va X(x,y) noma’lumlardan bog‘liq ikkita differensial tenglamalar
sistemasiga ega bo‘ldik. Hosil qilingan (4.2.7) tenglamalar sistemasi haqiqiy
xarakteristikali bir oilaga mansub bo‘lsin.
∂y
∂x=−P+cos 2α
sin 2α ;
∂α
∂x=0. (4.2.8)
Bundan ko‘rinadiki qaralayotgan tenglamalar sistemasi parabolik ko‘rinishga ega.
(4.2.8) tenglamalar sistemasini integrallab quyidagilarni hosil qilamiz [77]:
α=C1= const ;
y= x⋅tg [α+(P+1)π
4 ]+C2.
(4.2.9)
(4.2.9) ga ko‘ra to‘g‘ri chiziq x o‘qiga nisbatan
α+(P+1)π
4 ga og‘ishgan, bu
esa og‘ish chegarasini bildiradi va bosh kuchlanish traektoriyasini ifodalaydi.
(4.2.8) tenglamalar sistemasidagi birinchi tenglamadan [6] ga ko‘ra
quyidagini hosil qilamiz
y= xtg [α+(P+1)π
4]+Φ (α). (4.2.10)
Φ(α)
-funksiya chegaraviy shartlardan aniqlanadi. (4.2.7) tenglamalar sistemasi
ikkinchi tenglamasida. (4.2.9) ni hisobga olsak xarakteristik chiziq atrofida
quyidagi shart bajariladi
dln X=−2P∂α
∂x⋅ dx
sin 2α.
(4.2.11)
(4.2.10) da
∂α
∂x hisobga olib, (4.2.7) ning ikkinchi tenglamasini integrallab,
quyidagi umumiy yechimni hosil qilamiz:
X= Ψ (α)
2x+(1− Pcos 2α)Φ'(α)
,
(4.2.12)
bu yerda
Ψ (α) - o‘zgaruvchi funksiya bo‘lib berilgan chegaraviy shartlardan
aniqlanadi. Tekis taqsimlangan kuchlanishlar integralini
α= сonst ; X=const o‘q
ichiga oladi.
Ψ (α)
shartlardan aniqlanib α(x;y) va X(x,y) qiyshiq chiziq C atrofida x,y
tekislikka nisbatan berilgan bo‘ladi. Qiyshiq chiziq C xarakteri (Koshi masalasi)](/data/documents/a6911912-4c3a-40a9-b0bf-d37f9ccc557f/page_7.png)

PLASTIKLIK SHARTLARIDA HOLAT TENGLAMALARI REJA: 1. Mizes-Genka plastiklik shartida holat tenglamasi 2. Tresk-Sen-Venan plastiklik shartida holat tenglamasi
1. Mizes-Genka plastiklik shartida holat tenglamasi Muvozanat tenglamasi (2.2.1) va Mizes-Genka (2.2.5) plastiklik shartlari kuchlanishlarning uchta σx,σy,τxy komponentasini o‘zida ifodalaydi. Ushbu sistema plastiklik muvozanati holati uchun (2.2.4,a) va (2.2.5,b) kuchlanish komponentalarini ko‘chish tezliklaridan bog‘liq bo‘lmagan hollarda ham yechish mumkin. Ushbu qaralayotgan masala tekis kuchlanganlik holatida sirt kuchlanishlari uchun statik aniq hisoblanadi. Agar τi= τT= σT √3 tenglik bajarilganda bosh kuchlanishlar (2.1.6) formulalar bilan aniqlanadi deb qabul qilsak, Mizes-Genka plastiklik sharti (2.2.5,b) ko‘rinishda bajariladi, deb qabul qilishimiz mumkin bo‘ladi. Ushbu τi= σT √3 shart bajarilganda (2.1.7) ifodalarni hisobga olib (4.2.1) differensial tenglamalarni ba’zi almashtirishlardan keyin quyidagicha yozish mumkin: (√3sin ω− cos ω⋅cos 2α)∂ω ∂x − cos ω sin 2α∂ω ∂y +2sin ω(sin 2α∂α ∂x − cos 2α ∂α ∂ y)= 0; ( 4.1.1) cos ω⋅sin 2α∂ω ∂x − (√3sin ω +cos ω⋅cos 2α)∂ω ∂y − +2sin ω (cos 2α∂α ∂x +sin 2α∂α ∂y)= 0. Shunday qilib, qaralayotgan sistema tekis kuchlanganlik holati uchun ikkita noma’lum funksiya ω (x,y) va α(x,y) dan bog‘liq ikkita differensial tenglamalar sistemasiga kelmoqda. Ushbu tenglamalar sistemasi yechimi shu yechimlarning qanday turga mosligini (giperbola, parabola, ellips) xarakterlaydi. Ushbu sistemalar tipini aniqlash uchun bir nechta chiziqlarni L[x(S), y(S)] bog‘liq bo‘lgan funksiyalar α(S) va ω (S) larni qarab chiqamiz. Integral sirti orqali o‘tgan L ni quyidagicha yozamiz: ∂α ∂x dx + ∂α ∂ y dy = dα ; ∂ω ∂x dx +∂ω ∂ y dy = dω . (4.1.2) Egri chiziqli urinma integrali sirtidagi L xususiy hollarda quyidagicha bo‘ladi; ∂α ∂x ; ∂α ∂y ; ∂ω ∂x ; ∂ω ∂y . Hosil qilingan (4.1.1) va (4.1.2) tenglamalarni L orqali chiziqli algebraik tenglamalar ko‘rinishida yozish mumkin.
∂y ∂x = √3sin 2α± √3− ctg 2ω √3cos 2α− ctg ω. (4.1.3) Ushbu bog‘lanishlarni ω(x,y) va α(x,y) orqali noma’lum funksiyalar orqali yozish mumkin dα ± 1 2√3− ctg 2ω dω = 0. (4.1.4) Shunday qilib, qaralayotgan sistema differensial tenglamasi ikkita haqiqiy xarakterga ega bo‘ladi. Agar 3− ctg 2ω>0 π 6<ω <5π 6 yoki π 6 ⋅¿ω <11 6 π hollarda o‘rinli bo‘lsa (4.1.1) differensial tenglamalar sistemasi giperbola ko‘rinishda bo‘ladi. (4.1.1) tenglamalar sistemasi yechimi 2.1.2-rasmda tasvirlangan. Agar 3− ctg 2ω= 0 bo‘lsa (bu yerda ω quyidagi qiymatlarni qabul qilishi mumkin π 6;5π 6 ;7π 6 ;11 6 π ) qaralayotgan tenglamalar sistemasi parabola ko‘rinishida bo‘ladi. Agar 3− ctg 2ω<0 bo‘lsa haqiqiy xarakterga ega emas va (4.1.1) tenglamalar sistemasi elliptik ko‘rinishga ega. (4.1.1) tenglamalar sistemasini yechishda har xil oblastlar uchrashishi mumkin (giperbola, parabola, elliptik). Chunki o‘tish chegarasi noma’lum. Bu esa masalani yechishni qiyinlashtiradi. Bunda olingan natijalar bilan tekis kuchlanganlik holatidagi yechimlarni taqqoslash murakkablashadi. Agar kuchlanishlar ma’lum bo‘lsa (4.2.1,a) tenglamada tezliklar chiziqli bo‘ladi. Kuchlanishlar tenglamalarining giperboliklik sohasida tezliklar tenglamalari ham giperbolik bo‘ladi, bunda ularning xarakteristikalari ustma-ust tushadi. Faraz qilaylik, tezlikning uzilishli chizig‘i bo‘lmagan L chiziqda tezlik berilgan bo‘lsin. x , y koordinatalar sistemasidagi L chiziqda ixtiyoriy M nuqta tanlaymiz, bunda x koordinata L chiziqqa urinma bo‘lib yo‘nalgan. L chiziq bo‘ylab ∂vx ∂x, ∂vy ∂x hosilalar aniq, ∂vx ∂y , ∂vy ∂y hosilalar esa chegaralangan va (4.2.1,a) tenglamadan 2σx− σy= 0 va ∂vx ∂x= 0 shartlardan boshqa hollarda bir qiymatli aniqlanadi. Ushbu 2σx− σy= 0 shart kuchlanganlik holatining xarakteristika bo‘ylab bajariladi. Haqiqatdan ham, agar σx,σy,τxy kuchlanishlar L chiziqda uzluksiz va aniq bo‘lsa, u holda shu chiziqda ∂τxy ∂x ; ∂σx ∂x ; ∂σy ∂ y hosilalari aniq bo‘ladi va
∂τxy ∂y ; ∂σy ∂y lar (2.2.1) muvozanat shartlaridan aniqlanadi. ∂σy ∂y hosilani (2.2.5) oquvchanlik shartni y bo‘yicha differensiallash orqali aniqlash mumkin: ∂σx ∂ y (2σx− σy)+ ∂σy ∂y (2σy− σx)+6τxy ∂τxy ∂ y = 0. Agar 2σx− σy≠ 0 bo‘lsa, u holda ushbu ∂vx ∂x= 0 shart nisbiy chozilish tezligining xarakteristika chizig‘i bo‘ylab nolga tengligini anglatadi. 4.2. Tresk-Sen-Venan plastiklik shartida holat tenglamasi Tresk-Sen-Venan plastiklik sharti (2.2.6) dan σ1 va σ2 bosh kuchlanishlar ishoradan bog‘liq holda eng katta urinma kuchlanish har xil yuzalar bo‘yicha hosil bo‘lmoqda. Agar σ1 va σ2 larning ishoralari har xil bo‘lsa, u holda eng katta bosh kuchlanishlar hosil bo‘lishi 4.2.1-rasmlarda tesvirlangan. (σ1>01 σ2>01 bunda σ1>σ2) u holda maksimal kuchlanishlar. Agar ishoralar bir xil bo‘lsa σ2 o‘qida parallel yunalgan yuzalarda bo‘ladi, bu hol 4.2.1,b-rasmda tasvirlangan. Bunday holda Tresk-Sen-Venan plastiklik sharti quyidagi ko‘rinishni oladi, ya’ni σ1σ2<0 bo‘lsa σ1− σ2=±σT; (4.2.1) Agar σ1⋅σ2>0 bo‘lsa σ2=±σT; σ1=±σT; (4.2.2) bo‘ladi. Ushbu tenglama σ1− σ2 tekislikda oltiburchak shaklida bo‘ladi (4.2.2-rasm). Shunday qilib, tekis kuchlanganlik holati uchun Tresk-Sen-Venan plastiklik shartida oltiburchak qaralsa, Mizes-Genka plastiklik holatida ellips qaralgan edi, bu esa ushbu usulning afzalligini bildiradi. Bosh kuchlanishlar tezliklari deformatsiyalari ξ1 va ξ2 oltiburchakda qaralayotgan nuqta normali yunaltiruvchi kosinuslari nisbati orqali ifodalanadi. Bosh kuchlanish tezligi ξ3 siqilmaslik shartidan aniqlanadi: ξ1 + ξ2 + ξ3 =0. Oltiburchakning barcha ichki nuqtalarini AB, BC,CD,DE,EF,FA kabi belgilaymiz A,B,C,D,E,F lar esa oltiburchak qirralari uchlari hisoblanadi. U holda deformatsiya tezliklari quyidagicha bo‘ladi.
4.2.1,a-rasm 4.2.1,b-rasm A rejimda A σ1=σT:σ2=0; ξ1:ξ2=−1:q; AB σ1− σ2=− σT; ξ1:ξ2=−1:1; B σ2=σT;σ1= 0; ξ1:ξ2=q:1; BC σ1>0;σ2= σT; ξ1:ξ2= 0:1; C σ1=σ2=σT; ξ1:ξ2=−q:q; CD σ1=σT; σ2>0; ξ1:ξ2=1:0; DE σ1−σ2= σT; ξ1:ξ2=−1:(−1) va h.k. bu yerda 0≤q≤1.
