TAKRORLANUVCHI JARAYONLAR ALGORITMLARINI YARATISH. DASTURLAR TUZISH.

![1.15-rasm. 1 dan n gacha bo‘lgan sonlar yig‘indisini hisoblash blok-sxemasi
1.16-rasm. Hisoblash blok-sxemasi
1-misol . Birdan n gacha bo‘lgan natural sonlarning yig‘indisini hisoblash
algoritmini tuzaylik. Masalaning matematik modeli quyidagicha:
4- misol. Haqiqiy x sonining n chi darajasini hisoblash masalasi ko‘riladi.
5- misol . Quyidagi munosabatni hisoblash kerak bo‘lsin [2, 55-56 b.]:
agar ( i > n ) => (8);agar (i n) sharti tekshirilsin va u bajarilsa => (4) ; 7)≤
muhrlash (S).
Agar biror masalani yechish uchun zarur bo‘lgan
amallar ketma-ketligining ma’lum bir qismi biror
parametrga bog‘liq holda ko‘p marta
qayta bajarilsa , bunday jarayon takrorlanuvchi
algoritm deyiladi. Takrorlanuvchi algoritmlarga
misol sifatida odatda qatorlarning yig‘indisi yoki
ko‘paytmasini hisoblash jarayonlarini qarash
mumkin.Bu algoritmga mos blok-sxema 1.14-
rasmda keltirilgan.Bu algoritmga mos blok-sxema
1.15- rasmda keltirilgan.](/data/documents/8e286242-8d01-40e8-b648-236ff8e52e26/page_4.png)


![x n
/ n! .
n
n x i
n
S =1+2+ 3+...+
i =1
n(jarayonning matematik modeli: P =∏ i ) [2, 57-58 b.]. i =1
S = S + i ;
S = .
∑
S= 0 - natijaning boshlang‘ich qiymati;
S= S + i - natijaning joriy qiymatini hisoblang ;
S=0;
shartsiz o‘tish=> (4); 8) muhrlash (S).
Shunday qilib, x ning n chi darajasini hisoblash uchun takrorlanuvchi
jarayonni tashkil etish blok-sxemasi 1.16-rasmda keltirilgan.](/data/documents/8e286242-8d01-40e8-b648-236ff8e52e26/page_7.png)








TAKRORLANUVCHI JARAYONLAR ALGORITMLARINI YARATISH. DASTURLAR TUZISH. Algoritm hozirgi zamon matematikasining eng keng tushunchalaridan biri hisoblanadi. Algoritm (algorifm) so'zi o'rta asrlarda paydo bo'lgan bo'llb, buyuk mutafakkir bobokalonimiz Al-Xorazmiyning (783—855) ishlari bilan yevropaliklarning birinchi bor tanishishi bilan bog'liqdir. Bu ishlar ularda juda chuqur taassurot qoldirib algoritm (algorithmi) so'zining kelib chiqishiga sabab bo'ldiki, a Al-Xorazmiy ismining lotincha aytilishidir. U paytlarda bu so'z arablarda qo'llaniladigan o'nlik sanoq tizimi (sistemasi) va bu sanoq tizimida hisob-lash usulini bildirar edi. Shuni ta'kidlash lozimki, yevropaliklar tomonidan arab sanoq tizimining Al-Xorazmiy ishlari orqali o'zlashtirilishiga, keyinchalik hisoblash usullarining rivojlanishiga katta turtki bo'lgan. - sko‘paytirish jarayoni uchun boshlang‘ich qiymat berilishi: q = 1 ; - joriy natijani hisoblash: q = q * x ifoda bo‘yicha amalga oshiriladi.
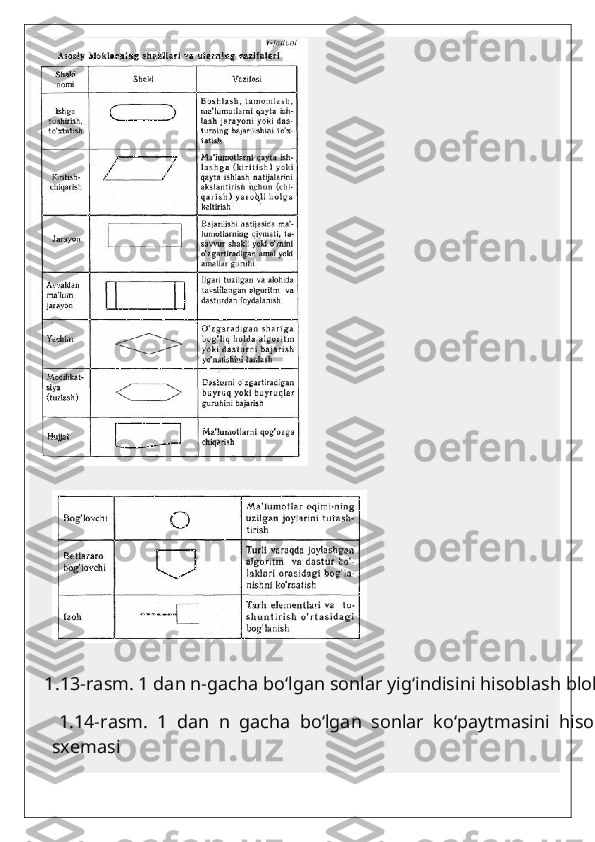
1.13-rasm. 1 dan n-gacha bo‘lgan sonlar yig‘indisini hisoblash blok-sxemasi 1.14-rasm. 1 dan n gacha bo‘lgan sonlar ko‘paytmasini hisoblash blok- sxemasi
1.15-rasm. 1 dan n gacha bo‘lgan sonlar yig‘indisini hisoblash blok-sxemasi 1.16-rasm. Hisoblash blok-sxemasi 1-misol . Birdan n gacha bo‘lgan natural sonlarning yig‘indisini hisoblash algoritmini tuzaylik. Masalaning matematik modeli quyidagicha: 4- misol. Haqiqiy x sonining n chi darajasini hisoblash masalasi ko‘riladi. 5- misol . Quyidagi munosabatni hisoblash kerak bo‘lsin [2, 55-56 b.]: agar ( i > n ) => (8);agar (i n) sharti tekshirilsin va u bajarilsa => (4) ; 7)≤ muhrlash (S). Agar biror masalani yechish uchun zarur bo‘lgan amallar ketma-ketligining ma’lum bir qismi biror parametrga bog‘liq holda ko‘p marta qayta bajarilsa , bunday jarayon takrorlanuvchi algoritm deyiladi. Takrorlanuvchi algoritmlarga misol sifatida odatda qatorlarning yig‘indisi yoki ko‘paytmasini hisoblash jarayonlarini qarash mumkin.Bu algoritmga mos blok-sxema 1.14- rasmda keltirilgan.Bu algoritmga mos blok-sxema 1.15- rasmda keltirilgan.
Bu jarayonga mos keladigan blok-sxemaning ko‘rinishi 1.13-rasmda tasvirlangan. Bu yig‘indini hisoblash uchun, avvalo, natiga boshlangich qiymatini S=0 va indeksning boshlangich qiymatini i =1 deb olamiz va joriy amallar S = S + i va i = i + 1 hisoblanadi. Bu erda birinchi va ikkinchi qadamlar uchun yig‘indi hisoblandi va keyingi qadamda i parametr yana bittaga orttiriladi va navbatdagi qiymat avvalgi yig‘indi S ga qo‘shiladi. Mazkur jarayon shu tartibda indeksning joriy qiymati i n≤ sharti bajarilmaguncha davom ettiriladi va natijada, izlangan yig‘indiga ega bo‘lamiz. Ushbu fikrlarni quyidagi so‘zlar orqali ifodalangan algoritm bilan ifodalash mumkin:chizish mumkin edi. Masalan, S = ∑ i yig‘indini xisoblash algoritmi tadqiqi i = 0; i = i + 1; i = 1 i ! i= 1 - indeksning boshlang‘ich qiymati; i= i+ 1- indeksning joriy qiymatinikeltiriladi. Bu masalani
