AXSHI STRUKTURALANGAN MUAMMOLARNI YECHISH PRINSIPI





















AXSHI STRUKTURALANGA N MUAMMOLARNI YECHISH PRINSIPI
YAXSHI STRUKTURALANGAN MUAMMOLARNI QAROR QABUL QILISH METODLARI: Yaxshi strukturalangan muammo quyidagi o‘ziga xoslik lar bilan xarakterlanadi: - Bo‘lajak harakatlar maqsadi obyektiv, ya’ni tashqaridan qo‘yilgan va menejer bilan bog‘liq emas; - Yechim variantlari (alternativlar)oldindan ma’lum, faqat yaxshisini tanlash kifoya;
YAXSHI STRUKTURALANGAN MUAMMOLARNI QAROR QABUL QILISH METODLARI: Yaxshi strukturalangan muammo quyidagi o‘ziga xoslik lar bilan xarakterlanadi: -Zaruriy resurslar ro‘yxati ma’lum, muammoni yechish uchun faqatgina ulardan kerakli sondagisini asoslash yetarli; - Muammoni yechish uchun hisobga olinuvchi faktorlar yoki funksiya shaklida aniq miqdoriy hisobga ega; - O‘zgaruvchilar o‘rtasidagi funksiyalar obyektiv va hosil qilinishi mumkin;
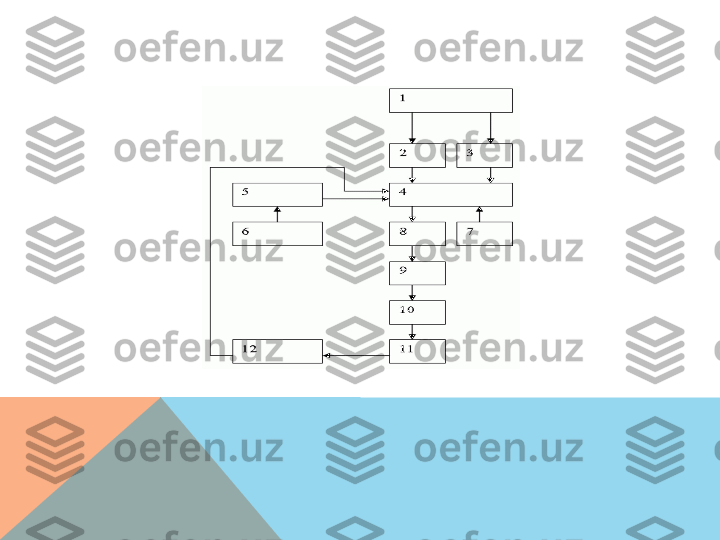
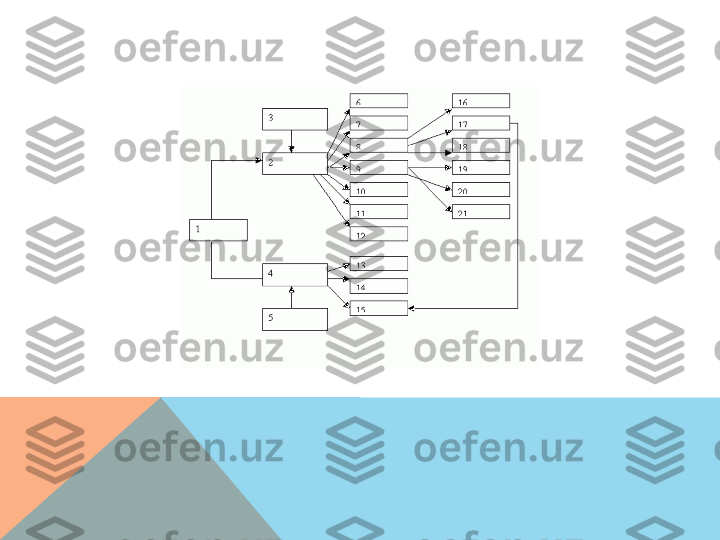
ЯХШИ СТРУКТУРАЛАНГАН МУАММОЛИ ЖАРАЁНЛАРНИ ТАДҚИҚ ҚИЛИШДА УШБУ АСОСИЙ БОСҚИЧЛАРНИ АЖРАТИБ КЎРСАТИШ МУМКИН: • Maqsadga erishish uchun raqobatlashadigan strategiyalarni aniqlash. • Amaliyotning matematik modelini qurish. • Raqobatlashadigan strategiyalar samaradorligini baholash. • Maqsadlarga erishish uchun maqbul strategiyani tanlash.
