Komleks sonlar tushunchsi. Komleks sonlarni qo’shish va ayirish










Mavzu:Komleks sonlar tushunchsi. Komleks sonlarni qo’shish va ayirish
Reja: Komleks sonlar tushunchsi. Komleks sonlarni qo’shish Komleks sonlarni ayirish
Kompleks son tushunchasi • Yoki ko‘rinishidagi songa ham kompleks son deyilib, bu kompleks sonning algebraik ko‘rinishi deyiladi. Bunda va haqiqiy sonlar mos ravishda kompleks sonning haqiqiy va mavhum qismi deb yuritiladi va quyidagicha simvol bilan belgilanadi: , (Realis va Imaginarius – lotincha so‘zlar bo‘lib, haqiqiy va mavhum demakdir)Ta` rif: kompleks son deb ma`lum bir tartibda berilgan bir juft va haqiqiy sonlarga aytiladi va quyidagicha yoziladi: .
Ushbu ib a va ib a ko‘rinishidagi sonlar o‘zaro qo‘shma kompleks sonlar deyiladi. 1 i – mavhum birlik bo‘lib, ,12 i , 3 i i ,1 4 i Shuning uchun: i i k 1 4 , 1 2 4 k i , i i k 3 4 , 1 4 k i Misollar. 1 2 25 4 102 i i , 1 3 50 4 203 i i , 1 2 128 4 514 i i
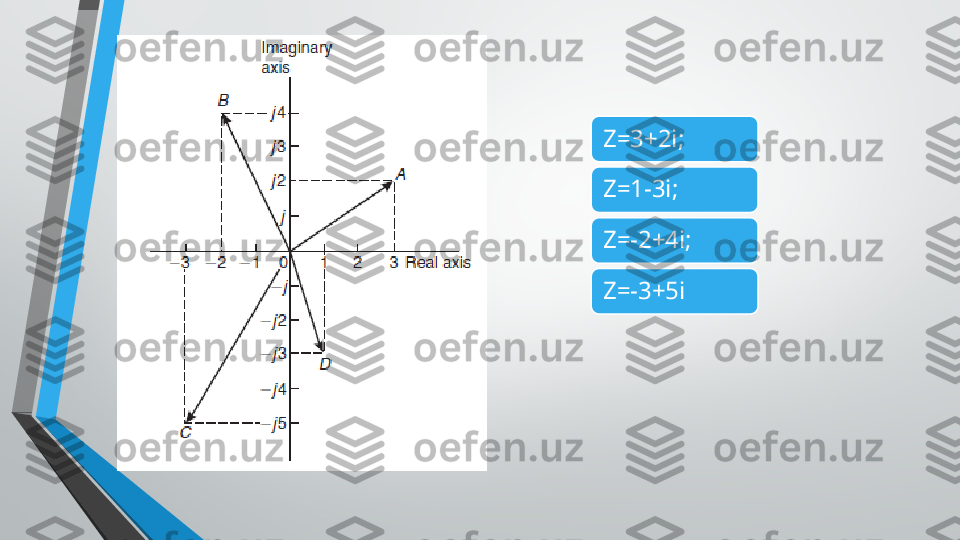
Z=3+2i; Z=1-3i; Z=-2+4i; Z=-3+5i
