DEKART DARAXTI (TREAP, DERAMID)

Загружено в:

12.08.2023

Скачано:

0

Размер:

249.171875 KB

Скачать

DEKART DARAXTI (TREAP, DERAMID)
Mundarija:
1.Kurs ishi uchun qo’yilgan mavzu……………………2
2.Kirish………………………………………………...4
3.Asosiy qism………………………………………….6
5.Xulosa……………………………………………….23
4.Foydalanilgan manba va adabiyotlar ro’yxati………24

Reja:
Kirish
1.Daraxt tushunchasi.
* Daraxt va unga ekvivalent tushunchalar
* Ikkilik daraxt
* Daraxtlarni Prufer kodida kodlash
2.Dekart daraxti .
* Dekart daraxti haqida tushuncha.
* Dekart daraxtini C va C++ tilida kodlash.
3.Xulosa
4.Foydalanilgan adabiyotlar ro’yxati

Kirish:
Algoritm kibernetika va matematikaning asosiy tushunchalaridan biri bo'lib, bu
atama o'rta asrlarda yashab ijod etgan buyuk o'zbek matematigi Al-Xorazmiy
nomidan kelib chiqqan. U IX asrning 825 yilidayoq o'zi kashf etgan o'nli sanoq
tizimida to‘rt arifmetika amallarini bajarish qoidalarini bergan. Arifmetika
amallarini bajarish jarayoni esa al-xorazm deb atalgan. Bu atama 1747 yildan
boshlab algorismus, 1950 yilga kelib algorifm deb ham ataldi. Fanda "Yevklid
algoritmi", "G'iyosiddin Koshiy algoritmi", "Laure algoritmi", "Markov algoritmi"
deb ataluvchi algoritmlar ma’lum algoritm tushunchasi tobora kengayib borib,
kibernetikaning nazariy va mantiqiy asosi hisoblangan algoritmlar nazariyasi
paydo bo'lgan. Kompyuterlar paydo bo'lishi bilan algoritm atamasi hozirgi ma'nosi
bilan axborot texnologiyalari sohasida eng asosiy atamalardan biri bo'lib qoldi.
Odatda algoritmlar u yoki bu hisoblashga doir masalalarni (computational
problems) yechish uchun tuziladi.
Qo'yilgan masala ushun yaratiladigan algoritmda kiruvchi va chiquvchi
ma’lumotlar muhim ahamiyatga ega, agar algoritm to'g'ri tuzilgan bo'Isa, ijrosi
(kompyuter) aniq natijalar beradi. Algoritm quyidagi xossalarga ega: aniqlilik,
tushunarlilik, ommaviylik, natijaviylik va diskretlik.
Aniqlik va tushunarlilik - deganda, algoritmda ijrochiga berilayotgan ko'rsatmalar
aniq mazmunda bo'lishi tushuniladi. Chunki ko'rsatmalardagi noaniqliklar
mo'ljallangan maqsadga erishishga olib keimaydi. Ijrochiga tavsiya etiladigan
ko'rsatmalar 8 tushunarli mazmunda bo‘lishi shart, aks holda ijrochi uni bajara
olmaydi. Ommavivlik - deganda, har bir algoritm mazmuniga ko‘ra bir turdagi
masalalaring barchasi uchun ham o‘rinli bo‘lishi,ya’ni umumiy bo‘lishi tushuniladi.
Natiiaviylik - deganda, algoritmda chekli qadamlardan so‘ng albatta natija bo’lishi
tushuniladi. Shuni ta'kidlash joizki, algoritm avvaldan ko‘zlangan maqsadga

erishishga olib kelmasligi ham mumkin. Bunga ba'zan algoritmning noto‘g‘ri
tuzilgani yoki boshqa xatolik sabab bo‘lishi mumkin, ikkinchi tomondan, qo‘yilgan
masala ijodiy yeshimga ega bolmasligi ham mumkin. Lekin salbiy natija ham deb
qabul qilinadi. Diskretlik - deganda, algoritmlami chekli qadamlardan tashkil qilib
bo'laklash imkoniyati tushuniladi. Algoritmlarga doir quyidagi masalalarini misol
sifatida keltirish mumkin:
• Talabani kundalik ishlarini tashkil etish;
• To‘rtburchak perimetri va yuzasini hisoblash;
• R radiusli doira yuzasini va aylana uzunligini topish;
• A1, A2 , А 3,..., An sonlarni toq elementlarini yig‘indisini topish;
• Berilgan ketma-ketlik sonlarni o‘sish (kamayish) tartibda joylashtirish va h.k.
Algoritm ning uchta turi mavjud: chiziqli, tarmoqlanuvchi va
takrorlanuvchi(siklik).
Chiziqli algoritmlar - hech qanday shartsiz faqat ketma-ket bajariladigan
jarayonlardir.
Tarmoqlanuvchi algoritmlar - ma’lum shartlarga muvofiq bajariladigan
jarayonlardir.
Takrorlanuvchi algoritmlar - biron-bir shart tekshirilishi yoki biron parametming
har xil qiymatlari asosida chekli ravishda takrorlanish yuz beradigan jarayonlardir.

Daraxt tushunchasi .
* Daraxt va unga ekvivalent tushunchalar .
Daraxt (grafik nazariyasi)
- Tree (graph theory)
Daraxtlar
6 ta vertikal va 5 ta qirrali etiketli
daraxt .
Vertices v
Qirralar v − 1
Xromatik raqam 2 agar v > 1
Grafiklar va parametrlar jadvali
D araxt bu yo'naltirilmagan grafik unda har qanday ikkitasi tepaliklar bilan
bog'langan to'liq bitta yo'l yoki unga teng ravishda
a ulangan asiklik yo'naltirilmagan grafik. A o'rmon har qanday ikkita tepalik
ulangan yo'naltirilmagan grafik ko'pi bilan yo'l, yoki ekvivalent ravishda asiklik
yo'naltirilmagan grafik yoki ekvivalent ravishda a uyushmagan
birlashma daraxtlar.
A polytree (yoki yo'naltirilgan daraxt yoki yo'naltirilgan daraxt yoki yakka
o'zi ulangan tarmoq ) a yo'naltirilgan asiklik grafik (DAG) asosiy yo'naltirilmagan
grafasi daraxtdir. A polyforest (yoki yo'naltirilgan o'rmon yoki yo'naltirilgan
o'rmon ) bu yo'naltirilgan asiklik grafik, uning ostida yo'naltirilmagan grafasi
o'rmondir.

Turli xil turlari ma'lumotlar tuzilmalari deb nomlangan daraxtlar yilda Kompyuter
fanlari bor asosiy grafikalar bu grafik nazariyadagi daraxtlar, garchi bunday
ma'lumotlar tuzilmalari odatda ildiz otgan daraxtlar . Ildizlangan daraxtni a deb
atash mumkin yo'naltirilgan ildizli daraxt , yoki uning barcha qirralarini ildizdan
uzoqlashtirishi - bu holda u an deb nomlanadi daraxtzorlik yoki daraxt - yoki
uning barcha qirralarini ildiz tomon yo'naltirganda - bu holda u an deb
nomlanadi daraxtzorlarga qarshi kurash ]
yoki daraxtda . Ildizlangan daraxtning
o'zi ba'zi mualliflar tomonidan yo'naltirilgan grafik sifatida aniqlangan. A ildiz
otgan o'rmon ildiz otgan daraxtlarning ajralgan birlashmasi. Ildizlangan o'rmon
boshqarilishi mumkin, deyiladi yo'naltirilgan ildizli o'rmon , yoki uning barcha
qirralarini har bir ildiz otilgan daraxtda ildizdan uzoqlashtirishi - bu holda u a deb
nomlanadi dallanma yoki o'rmondan tashqarida - yoki uning barcha qirralarini
har bir ildiz otilgan daraxtda ildiz tomon yo'naltirganda - bu holda u "an" deb
nomlanadi dallanishga qarshi yoki o'rmonda .
"Daraxt" atamasi 1857 yilda ingliz matematikasi Artur Keyli tomonidan kiritilgan .
A daraxt yo'naltirilmagan grafik G quyidagi teng sharoitlardan birini qondiradigan:
 G bu ulangan va asiklik (tsikllarni o'z ichiga olmaydi).
 G asiklikdir va agar mavjud bo'lsa oddiy tsikl hosil bo'ladi chekka ga qo'shiladi G .
 G ulanadi, lekin bo'ladi uzilgan agar biron bir chekka olib tashlansa G .
 G ulangan va 3-vertex to'liq grafik K
3 emas voyaga etmagan ning G .
 Har qanday ikkita tepalik G noyob bilan bog'lanishi mumkin oddiy yo'l .
Agar G juda ko'p tepaliklarga ega, deylik n ulardan, keyin yuqoridagi bayonotlar
ham quyidagi shartlardan biriga teng keladi:
 G ulangan va ega n − 1 qirralar.
 G ulangan va har biri subgraf ning G kamida nol yoki bitta hodisa qirralari bo'lgan
bitta tepalikni o'z ichiga oladi. (Anavi, G ulangan va 1-degeneratsiya .)
 G oddiy tsikllarga ega emas va bor n − 1 qirralar.
Grafik nazariyasining boshqa joylarida bo'lgani kabi tartib-nol grafigi (tepaliklarsiz
grafika) odatda daraxt deb hisoblanmaydi: u grafika sifatida bo'shliq bilan
bog'langan bo'lsa (istalgan ikkita tepalik yo'l bilan bog'lanishi mumkin), u emas 0
ulangan (yoki hatto (-1) -bog'langan) algebraik topologiyada, bo'sh bo'lmagan
daraxtlardan farqli o'laroq va "qirralarga qaraganda yana bitta vertikal"
munosabatini buzadi. Biroq, uni nol daraxtlardan tashkil topgan o'rmon deb
hisoblash mumkin.
An ichki tepalik (yoki ichki tepalik yoki filial tepasi ) ning tepasi daraja kamida
2. Xuddi shunday, an tashqi tepalik (yoki tashqi tepalik , terminal
tepasi yoki barg ) 1 darajali tepalikdir.
An kamaytirilmaydigan daraxt (yoki ketma-ket kamaytirilgan daraxt ) - bu 2-
darajali tepalik bo'lmagan daraxt (ketma-ketlikda sanab o'tilgan)

Ildizli daraxt
A ildiz otgan daraxt - bu bitta vertex belgilangan daraxt ildiz . Ildizlangan
daraxtning qirralariga ham tabiiy yo'nalish berilishi
mumkin uzoqda yoki tomonga ildiz, bu holda struktura a ga aylanadi yo'naltirilgan
ildizli daraxt . Yo'naltirilgan ildizli daraxt ildizdan uzoqroq yo'nalishga ega bo'lsa, u
an deb ataladi daraxtzorlik yoki daraxt ; u ildizga yo'naltirilgan bo'lsa, u an
deyiladi daraxtzorlarga qarshi kurash yoki daraxtda . The daraxt
buyurtmasi bo'ladi qisman buyurtma berish bilan daraxtning tepalarida siz < v agar
va faqat ildizdan noyob yo'l bo'lsa v orqali o'tadi siz . A bo'lgan daraxt subgraf ba'zi
bir grafikalar G a oddiy daraxt agar har bir chetning uchlari bo'lsa G har qanday
uchlari daraxtning tepalari bo'lganda, ushbu daraxt tartibida taqqoslash mumkin
( Diestel 2005 yil , p. 15). Ildizli daraxtlar, ko'pincha qo'shimcha tuzilishga ega,
masalan, har bir tepada qo'shnilarga buyurtma berish, bu informatika
ma'lumotlarining asosiy tuzilishi; qarang daraxt ma'lumotlari tuzilishi .
Daraxtlar ildizga ega bo'lishi kerak bo'lgan sharoitda, hech qanday belgilanmagan
ildizsiz daraxt a deb nomlanadi bepul daraxt .
A belgilangan daraxt har bir tepaga noyob yorliq berilgan daraxtdir. Belgilangan
daraxtning tepalari n tepaliklarga odatda 1, 2, ..., yorliqlari beriladi n . A rekursiv
daraxt - vertikal yorliqlar daraxt tartibini hurmat qiladigan (ya'ni, agar) siz < v ikki
tepalik uchun siz va v , keyin yorlig'i siz belgisidan kichikroq v ).
Ildizlangan daraxtda ota - ona tepalikning v ga ulangan
tepalikdir v ustida yo'l ildizga; har bir tepalikning ota-onasi bo'lmagan ildizdan
tashqari o'ziga xos ota-onasi bor. A bola tepalikning v uning tepasi v ota-
ona. An ko'tarilgan tepalikning v ning ota-onasi bo'lgan har qanday tepalik v yoki
(rekursiv ravishda) ning ota-onasining ko'taruvchisi v . A avlod tepalikning v ning
farzandi bo'lgan har qanday tepalik v yoki (rekursiv) har qanday farzandning
avlodi v . A qardosh tepaga v daraxtga o'xshash har qanday boshqa
tepalikdir v . A barg bolalari bo'lmagan tepalik. An ichki tepalik bu barg emas
vertexdir.
The balandlik Ildizli daraxtdagi tepalik - bu tepalikdan bargga tushadigan eng uzun
yo'lning uzunligi. The balandlik daraxtning ildizi balandligi. The chuqurlik vertex -
bu uning ildiziga boradigan yo'lning uzunligi ( ildiz yo'li ). Bu odatda o'z-o'zini
muvozanatlashtiradigan turli xil daraxtlarni manipulyatsiya qilishda kerak
bo'ladi, AVL daraxtlari jumladan. Ildiz chuqurligi nolga, barglari balandligi nolga,
va faqat bitta tepalikka ega bo'lgan daraxt (shuning uchun ham ildiz, ham barg)
chuqurlik va balandlik nolga ega. An'anaviy ravishda bo'sh daraxt (agar ruxsat
berilsa, tepaliksiz daraxt) chuqurligi va balandligi −1 ga ega.

Xususiyatlari
 Har bir daraxt a ikki tomonlama grafik . Graf ikki tomonlama, agar u faqat toq
uzunlikdagi tsikllarni o'z ichiga olmasa. Daraxt umuman tsikllarni o'z ichiga
olmaganligi sababli, u ikki tomonlama.
 Har bir daraxt a o'rtacha grafik .
 Faqatgina har bir daraxt hisoblash uchun ko'plab tepaliklar a planar grafik .
 Har qanday bog'langan grafik G tan oladi a yoyilgan daraxt , bu har bir tepalikni o'z
ichiga olgan daraxtdir G va uning qirralari qirralar G .
 Faqatgina har bir bog'langan grafik hisoblash uchun ko'plab tepaliklar odatdagi
daraxt daraxtini tan olishadi ( Diestel 2005 yil , 8.2.4-rasm).
 Bilan bog'liq grafikalar mavjud sanoqsiz oddiy daraxt daraxtini qabul qilmaydigan
ko'plab tepaliklar ( Diestel 2005 yil , 8.5.2-rasm).
 Bilan har bir cheklangan daraxt n tepaliklar, bilan n > 1 , kamida ikkita terminal
tepalikka ega (barglar). Bu barglarning minimal soni xarakterlidir yo'l grafikalari ;
maksimal son, n − 1 , faqat tomonidan erishiladi yulduz grafikalar . Barglarning soni
hech bo'lmaganda maksimal tepalik darajasidir.
 Daraxtdagi har qanday uchta tepalik uchun ularning orasidagi uchta yo'l to'liq bitta
vertikalga ega (bu tepalik " o'rtacha ushbu uchta tepadan).
 Har bir daraxtda a markaz bitta tepalik yoki ikkita qo'shni tepadan iborat. Markaz
har bir eng uzun yo'lda o'rta tepalik yoki o'rta ikkita tepalikdir. Xuddi shunday, har
bir n -vertex daraxtida bitta tepalik yoki ikkita qo'shni tepadan tashkil topgan
santroid mavjud. Birinchi holda tepalikni olib tashlash daraxtni kamroq daraxtlarga
bo'linadi n / 2 tepalik. Ikkinchi holda, ikkita tsentroidal tepaliklar orasidagi
qirralarning olib tashlanishi daraxtni ikkita pastki daraxtga bo'linadi. n / 2 tepalik.
Keylining formulasi borligini bildiradi n n −2
daraxtlar n belgilangan tepaliklar.
Klassik isboti foydalanadi Prüfer ketma-ketliklari , bu tabiiy ravishda yanada kuchli
natija ko'rsatmoqda: tepaliklari 1, 2, ..., bo'lgan daraxtlar
soni n daraja d
1 , d
2 , ..., d
n navbati bilan multinomial koeffitsient
Umumiy muammo - bu hisoblash daraxtlar ichida yo'naltirilmagan grafik
tomonidan hal qilingan matritsa daraxti teoremasi . (Cayley formulasi - bu a-dagi
daraxtlarning tarqalishidagi alohida holat to'liq grafik .) Barcha kichik daraxtlarni
o'lchamidan qat'i nazar hisoblashning o'xshash masalasi # P tugadi umumiy
holatda ( Jerrum (1994) ).

Ikkilik daraxti
Ikkilik daraxt - Binary tree
B daraxti .
Ildiz tuguni bilan qiymati 9 bo'lgan va balandligi 3 ga teng bo'lgan ikkilik daraxt,
yuqoridagi daraxt muvozanatsiz va tartiblanmagan.
Ikkilik daraxt a daraxt ma'lumotlari tuzilishi unda har bir tugun ko'pi bilan
ikkitadan bolalar deb nomlangan chap bola va o'ng bola . A rekursiv ta'rif faqat
foydalanish to'plam nazariyasi tushunchalar shundan iboratki (bo'sh bo'lmagan)
ikkilik daraxt a panjara ( L , S , R ), qayerda L va R ikkilik daraxtlar yoki bo'sh
to'plam va S a singleton to'plami ildizni o'z ichiga olgan. Ba'zi mualliflar
ikkitomonlama daraxtga ham bo'sh to'plam bo'lishiga ruxsat berishadi.
A dan grafik nazariyasi bu erda aniqlangan istiqbolli, binar (va K-ary) daraxtlar
aslida daraxtzorlar . Ikkilik daraxtni shunday deb ham atash mumkin ikki
tomonlama daraxtzor - bu juda qadimgi dasturlash kitoblarida uchraydigan
atama, ilgari zamonaviy informatika terminologiyasi ustun kelgan. Ikkilik daraxtni
an deb talqin qilish ham mumkin yo'naltirilmagan , a o'rniga yo'naltirilgan grafik ,
bu holda ikkilik daraxt an buyurdi , ildiz otgan daraxt . Ba'zi mualliflar
foydalanadilar ikkilik daraxt o'rniga ikkilik daraxt daraxtning ildiz otganligini
ta'kidlash uchun, lekin yuqorida ta'riflanganidek, ikkilik daraxt har doim ildiz
otadi. Ikkilik daraxt - bu buyurtma qilingan alohida holat K-ary daraxti ,
qayerda k 2.
Ikkilik daraxt turlari
Daraxtlar terminologiyasi yaxshi standartlanmagan va shuning uchun ham
adabiyotda turlicha .
 A ildiz otgan ikkilik daraxt bor ildiz tuguni va har bir tugunning ko'pi bilan ikkita
bolasi bor.

To'liq binar daraxt
An ajdodlar jadvali mukammal chuqurlik-4 ikkilik daraxtiga xaritalar.
 A to'liq ikkilik daraxt (ba'zan a deb ham nomlanadi to'g'ri yoki samolyot ikkilik
daraxt) har bir tugunda 0 yoki 2 boladan iborat bo'lgan daraxt. To'liq ikkilik
daraxtni aniqlashning yana bir usuli bu rekursiv ta'rif . To'liq ikkilik daraxt ham:
o Bitta tepalik.
o Ildiz tugunida ikkita kichik daraxt bo'lgan daraxt, ikkalasi ham to'liq ikkilik
daraxtlardir.
 A to'liq har darajadagi ikkilik daraxt, ehtimol oxirgisi bundan mustasno , to'liq
to'ldirilgan va oxirgi darajadagi barcha tugunlar iloji boricha chaproq. U 1 dan 2
gacha bo'lishi mumkin h oxirgi darajadagi tugunlar h . Muqobil ta'rif - eng to'g'ri
barglari (ehtimol barchasi) olib tashlangan mukammal daraxt. Ba'zi mualliflar
ushbu atamadan foydalanadilar to'liq Buning o'rniga quyida keltirilgan mukammal
ikkilik daraxtga murojaat qilish, bu holda ular ushbu turdagi daraxtlarni (ehtimol
oxirgi daraja to'ldirilmagan holda) deyarli to'liq ikkilik daraxt yoki deyarli
yakunlandi ikkilik daraxt. To'liq ikkilik daraxt massiv yordamida samarali tarzda
ifodalanishi mumkin .
To'liq ikkilik daraxt (bu to'liq emas)
 A mukammal ikkilik daraxt - bu barcha ichki tugunlarning ikkita farzandi bo'lgan
ikkilik daraxt va barcha barglar bir xil chuqurlik yoki bir xil Daraja . Barkamol

binar daraxtning misoli (qarindosh bo'lmagan). ajdodlar jadvali insonning ma'lum
bir chuqurlikka ega bo'lishi, chunki har bir odamning ikkita biologik ota-onasi
(bitta onasi va bitta otasi) bor. Agar ota-bobolar jadvalida onaning va otaning
ma'lum bir tugun uchun har doim bir tomonda bo'lishi sharti bilan, ularning jinsi
chap va o'ng bolalarning o'xshashligi sifatida qaralishi mumkin, bolalar bu erda
algoritmik atama sifatida tushuniladi. Shuning uchun mukammal daraxt har doim
to'liq bo'ladi, ammo to'liq daraxt mukammal bo'lishi shart emas.
 In cheksiz to'liq ikki tomonlama daraxt, har bir tugunda ikkita bola bor (va
shuning uchun darajalar to'plami shunday) nihoyatda cheksiz ). Barcha
tugunlarning to'plami son-sanoqsiz, ammo ildizdan chiqadigan barcha cheksiz
yo'llarning to'plamini hisoblash mumkin emas. doimiylikning kardinalligi . Buning
sababi shundaki, bu yo'llar buyurtmani saqlash bilan mos keladi bijection ning
nuqtalariga Kantor o'rnatilgan , yoki (a misolidan foydalanib Stern-Brocot daraxti )
ijobiy to'plamga mantiqsiz raqamlar .
 A muvozanatli ikkilik daraxt - bu har bir tugunning chap va o'ng pastki daraxtlari
balandligi bo'yicha 1 dan ko'p bo'lmagan farq qiladigan ikkilik daraxt
tuzilishi. ]
Ikkala daraxtni ham ko'rib chiqish mumkin, u erda hech qanday barg
bargdan boshqa bargga qaraganda ancha uzoqroq joylashgan. (Turli xil
muvozanatlash sxemalari "ancha uzoqroq" ning turli xil ta'riflariga imkon beradi. ]
)
 A buzilib ketgan (yoki patologik ) daraxt - bu har bir ota-ona tugunida faqat bitta
bog'langan tugun mavjud. Bu shuni anglatadiki, daraxt o'zini a kabi
tutadi bog'langan ro'yxat ma'lumotlar tuzilishi .
Ikkilik daraxtlarning xususiyatlari
 Tugunlarning soni to'liq ikkilik daraxtda, hech bo'lmaganda va ko'pi
bilan , qayerda bo'ladi balandlik daraxtning. Faqatgina ildiz tugunidan
iborat daraxtning balandligi 0 ga teng.
 Barg tugunlari soni mukammal ikkilik daraxtda, bo'ladi chunki bargsiz
(ichki a) tugunlarning soni .
 Bu degani, to'liq binar daraxt bilan barglari bor tugunlar.
 A muvozanatli to'liq ikkilik daraxt, (qarang ship funktsiyasi ).
 A mukammal to'liq ikkilik daraxt, shunday qilib .
 Ning ikkilik daraxtidagi bo'sh havolalar soni (ya'ni tugunlarning yo'q
bolalari) n tugunlari ( n +1).
 A-dagi ichki tugunlarning soni to'liq binar daraxt n tugunlar .
 Bilan har qanday bo'sh bo'lmagan ikkilik daraxt uchun n
0 barg tugunlari va n
2 2-
darajali tugunlar, n
0 = n
2 + 1.

Umumiy daraxtlarni ikkilik daraxtlar sifatida
kodlash
Umumiy buyurtma qilingan daraxtlar va ikkilik daraxtlar o'rtasida birma-bir
xaritalash mavjud, ular ayniqsa foydalaniladi Lisp umumiy tartibli daraxtlarni
ikkilik daraxtlar sifatida ko'rsatish. Umumiy buyurtma qilingan daraxtni ikkilik
daraxtga aylantirish uchun biz faqat umumiy daraxtni chapdan o'ngga birodarlik
usulida namoyish etishimiz kerak. Ushbu namoyish natijasi, agar boshqa nuqtai
nazardan qaralsa, avtomatik ravishda ikkilik daraxt bo'ladi. Har bir
tugun N buyurtma qilingan daraxtda tugunga to'g'ri keladi N ' ikkilik daraxtda;
The chap ning farzandi N ' ning birinchi bolasiga mos keladigan tugun N ,
va to'g'ri ning farzandi N ' ga to'g'ri keladigan tugun N keyingi birodar ---, ya'ni
ota-onasining farzandlari orasida navbatdagi tugun N . Umumiy tartib daraxtining
bu ikkilik daraxt tasvirini ba'zida a deb ham atashadi chap bolada o'ng aka-uka
ikkilik daraxt (shuningdek, LCRS daraxti, juft zanjirli daraxt, filial-merosxo'r
zanjiri deb ham ataladi).
Bu haqda o'ylashning bir usuli shundaki, har bir tugunning bolalari a bog'langan
ro'yxat , ular bilan birga zanjirlangan to'g'ri maydonlari va tugun faqat ushbu
ro'yxatning boshiga yoki boshiga ko'rsatgichga ega chap maydon.
Masalan, chap tomondagi daraxtda A ning 6 ta farzandi bor {B, C, D, E, F, G}.
Uni o'ngdagi ikkilik daraxtga aylantirish mumkin .
Ikkilik daraxtni yon tomonga burilgan, chap qora qirralarni ko'rsatadigan asl daraxt
deb hisoblash mumkin birinchi bola va ko'k rangning o'ng qirralari keyingi birodar .
Chapdagi daraxt barglari Lispda shunday yozilgan bo'lar edi:
(((N O) I J) C D ((P) (Q)) F (M))
bu chap bolali tugunlarda hech qanday harflarsiz, xotirada o'ngdagi ikkilik daraxt
sifatida amalga oshiriladi.

$Daraxtlarni Prufer usulida kodlash Prufer kodi nima? Daraxt berilgan (ildiz otgan daraxt sifatida emas, balki grafik sifatida ko'rsatilgan) n 1 dan n gacha bo'lgan yorliqlar bilan belgilangan tugunlar, Prufer kodi daraxtni noyob tarzda aniqlaydi. Ketma-ketlik n-2 qiymatlarga ega. Daraxtning Prufer kodini qanday olish mumkin? 1. Prufer kodini bo'sh deb boshlang. 2. Eng past yorliqli barg bilan boshlang x deb ayting. uni daraxtning qolgan qismiga ulaydigan tepalikni toping y deb ayting. X ni daraxtdan olib tashlang va Prufer kodiga y qo'shing 3. Ikkita tugun qolguncha 2-bosqichni takrorlang. 1 dan n gacha yorliqli daraxt. 5 / \ 1 4 / \ 2 3 PruferCode = {} Eng past yorliq bargi 2, biz uni daraxtdan olib tashlaymiz va boshqa vertexni qo'shing (uni daraxtga ulash) prufer kodiga Daraxt endi bo'ladi 5 / \ 1 4 \ 3 Prufer kod bo'ladi = {1} Eng past yorliq bargi 3, biz uni daraxtdan olib tashlaymiz$ $va boshqa vertexni qo'shing (uni daraxtga ulash) prufer kodiga Daraxt endi bo'ladi 5 / \ 1 4 Prufer kod bo'ladi = {1, 1} Eng past etiketka bargi 1, uni daraxtdan olib tashlaymiz va boshqa vertexni qo'shing (uni daraxtga ulash) prufer kodiga Daraxt endi bo'ladi 5 \ 4 Prufer kod bo'ladi = {1, 1, 5} Hozir bizda faqat ikkita tugun qoldi, shuning uchun biz to'xtaymiz. Berilgan Prufer kodidan daraxt qanday quriladi? Kiritish : (4, 1, 3, 4) Chiqish: quyidagi daraxtning qirralari 2----4----3----1----5 | 6 Kirish : (1, 3, 5) Chiqish: quyidagi daraxtning qirralari 2----1----3----5----4 Berilgan Prufer kodining uzunligi m bo'lsin. g'oya m+2 uchlarining bo'sh grafigini yaratishdir. Birinchi elementni ketma-ketlikdan olib tashlaymiz. Joriy ketma- ketlikning birinchi elementi x bo'lsin. keyin berilgan ketma-ketlikda mavjud$

bo'lmagan va hali daraxtga qo'shilmagan eng kam qiymatni topamiz. Ushbu qiymat
y bo'lsin. biz x dan y gacha chekka qo'shamiz va bu qadamni takrorlaymiz.
Yuqoridagi birinchi misol bilan daraxtni qurish algoritmini tushunaylik:

Kiritish : (4, 1, 3, 4)
1-qadam: dastlab 6 ta tepalikning bo'sh grafigini hosil qilamiz
va ketma-ketlikdan 4 ni oling.
2-qadam: 1 dan 6 gacha, eng kichik tepalik emas
Prufer ketma - ketligi 2.
3-qadam: 2 va 4 orasida chekka hosil qilamiz.
2----4 1 3 5 6
Qadam 4: ketma-ketlikda keyingi 1 va tegishli
eng kam darajaga ega vertex 5 ga teng (2 bo'lgani kabi
ko'rib chiqildi).
2----4 1----5 3 6
Qadam 5: ketma - ketlikda keyingi 3 va tegishli
eng kam darajali vertex 1 ga teng
(sifatida 1 endi qolgan Prufer ketma qismi emas)
2----4 3----1----5 6
6-qadam: keyingi ketma-ketlikda 4 va tegishli vertex
eng kam daraja bilan 3 (sifatida 3 ko'rib qilinmagan
sifatida ketma-ketlikda yanada mavjud emas)
2----4----3----1----5 6
7-qadam: nihoyat 1 dan 6 gacha (4) ikkita tepalik qoldiriladi
va 6) shuning uchun biz ularga qo'shilamiz.
2----4----3----1----5
|
6
Bu 6 ta tepalikdagi kerakli daraxt.
Quyidagi amalga oshirish hisoblanadi.

$ C++ // C++ program to construct tree from given Prufer Code #include <bits/stdc++.h> using namespace std; // Prints edges of tree represented by give Prufer code void printTreeEdges(int prufer[], int m) { int vertices = m + 2; int vertex_set[vertices]; // Initialize the array of vertices for (int i = 0; i < vertices; i++) vertex_set[i] = 0; // Number of occurrences of vertex in code for (int i = 0; i < vertices - 2; i++) vertex_set[prufer[i] - 1] += 1; cout << "\nThe edge set E(G) is :\n"; // Find the smallest label not present in // prufer[]. int j = 0; for (int i = 0; i < vertices - 2; i++) {$ $for (j = 0; j < vertices; j++) { // If j+1 is not present in prufer set if (vertex_set[j] == 0) { // Remove from Prufer set and print // pair. vertex_set[j] = -1; cout << "(" << (j + 1) << ", " << prufer[i] << ") "; vertex_set[prufer[i] - 1]--; break; } } } j = 0; // For the last element for (int i = 0; i < vertices; i++) { if (vertex_set[i] == 0 && j == 0) { cout << "(" << (i + 1) << ", "; j++; } else if (vertex_set[i] == 0 && j == 1) cout << (i + 1) << ")\n"; }} // Driver code int main()$ { int prufer[] = { 4, 1, 3, 4 };
int n = sizeof(prufer) / sizeof(prufer[0]);
printTreeEdges(prufer, n);
return 0;
}
Chiqish:
Chekka to'plam E (G) dir :
(2, 4) (5, 1) (1, 3) (3, 4) (4, 6)
Dekart daraxti.
* Dekart daraxti haqida tushuncha .
Dekart daraxti
De k art daraxti
ingliz tili. Treap

{ int prufer[] = { 4, 1, 3, 4 };
int n = sizeof(prufer) / sizeof(prufer[0]);
printTreeEdges(prufer, n);
return 0;
}
Chiqish:
Chekka to'plam E (G) dir :
(2, 4) (5, 1) (1, 3) (3, 4) (4, 6)
Dekart daraxti.
* Dekart daraxti haqida tushuncha .
Dekart daraxti
De k art daraxti
ingliz tili. Treap

Turi Ikkilik qidiruv daraxti
Ixtiro yili 1989
Muallif Raimund Siedel, Cecilia Aragon
Qiyinchilik ichida O-simvolizm
O'rtacha Eng yomon holatda
Qurilish
Qidiruv
Qo'shish
Olib tashlash
Dekart daraxti - tugunlarida saqlanadigan ikkilik daraxt :
 o'ng va chap soxta ma'lumotlarga havolalar;
 ota-ona tuguniga havola (ixtiyoriy);
 x va y tugmalari, x kalitidagi ikkilik qidiruv daraxti va y kalitidagi
ikkilik qoziq ; ya'ni, har qanday daraxt tuguniga n :
o o'ng (chap) podderevning kalitlari x tugunlari katta (kamroq) yoki n
tugunining x tugmachasiga teng;
o o'ng va chap bolalarning kalitlari y tugunlari tugmachasi y tugun n ga teng .
Ota-ona tuguniga havola qilish shart emas, faqat daraxtni qurish uchun chiziqli
algoritm uchun kerak.
Dekart daraxti odatiy ma'noda o'zini muvozanatlashtirmaydi va uni quyidagi
sabablarga ko'ra qo'llaydi:
 Misol uchun, qizil-qora kabi haqiqiy muvozanatlashgan daraxtlar bilan
taqqoslash osonroq.
 Agar kalitlar bo'lsa, "o'rtacha" yaxshi ishlaydi y tasodifan tarqatildi.

 Odatda, daraxtni saralash uchun operatsiya " x kaliti bilan " x
0 dan kam "va" x
0 dan kam
bo'lmagan" " O ( h ) uchun ishlaydi, bu erda h daraxtning balandligi. Qizil va
qora daraxtlarda tugunlarning muvozanatini va rangini tiklash kerak bo'ladi.
Kartezyen daraxtining kamchiliklari:
 Katta saqlash xarajatlari: har bir element bilan birgalikda ikki yoki uchta
ko'rsatgich va tasodifiy kalit y saqlanadi.
 Kirish tezligi O ( n )eng yomon holatda bo'lsa ham. Shuning uchun, Dekart
daraxti, masalan, OS yadrosida qabul qilinishi mumkin emas .
Rene Descartes (FR. René Descartes (lotin René Descartes) — XVII asrning buyuk
fransuz matematigi va faylasufi.
Rene Descartes Descartes daraxtining yaratuvchisi emas, balki u biz biladigan va
sevgan cartesian koordinata tizimining yaratuvchisi.
Dekart daraxti ham shunday belgilanadi va quriladi:
 Biz samolyotga bir qator murojaat qilamiz n nuqta. Ularning x nima uchun biz
kalit deb ataymiz va y birinchi o'ringa.
 Eng yuqori nuqtani tanlang (eng katta y va agar bir nechta bo'lsa - har qanday) va
uni ildiz deb ataymiz .
 Chapdagi barcha tepaliklardan (kichikroq) x) ildizdan biz xuddi shu jarayonni
qayta ishga tushiramiz. Agar chapda kamida bitta tepalik bo'lsa, chap qismning
ildizini hozirgi ildizning chap o'g'li sifatida qo'shing.
 Xuddi shunday, biz o'ng tomondan boshlaymiz va o'ng o'g'lining ildizini
qo'shamiz.
E'tibor bering, agar hamma narsa bo'lsa y va x turli xil, keyin daraxt noyob tarzda
qurilgan.
Agar siz olingan strukturani tekislikda chizishingiz kerak bo'lsa, unda siz daraxtni
olasiz — an'anaga ko'ra, ildiz yuqoriga ko'tariladi:

Shunday qilib, Dekart daraxti bir vaqtning o'zida ikkilik daraxtdir x va bir guruh y.
Shuning uchun u ko'plab muqobil nomlar bilan keldi:
 Deramid ( daraxt + Piramid)
 Pivo ( piramida + daraxt)
 Tovuq (shamlardan + daraxt)
 Treap (tree + heap)
 Insert ( X, Y) - o (log N) uchun o'rtacha
daraxtga yangi element qo'shiladi.
Y ustuvorligi funktsiyaga o'tkazilmaydigan va tasodifan tanlangan variant
mumkin(garchi daraxtda boshqa Y bilan mos kelmasligi kerak).
 Qidiruv (X) - o (log N) uchun o'rtacha
belgilangan asosiy qiymati X bo'lgan elementni qidiradi.odatiy ikkilik qidiruv
daraxti bilan bir xil tarzda amalga oshiriladi.
 O'chirish (X) - o (log N) uchun o'rtacha
elementni qidiradi va uni daraxtdan olib tashlaydi.
 Build (X
1 , ..., X
N ) - o (N)
uchun qiymatlar ro'yxatidan daraxt quradi. Bu operatsiya chiziqli vaqtda amalga
oshirilishi mumkin (taxmin deb qadriyatlar x
1 ,.... X
N tartiblangan), lekin bu erda
amalga oshirish ko'rib chiqilmaydi.
Bu erda faqat eng oddiy dastur ishlatiladi - ketma-ket qo'ng'iroqlar shaklida, ya'ni o
(n log N) uchun.
 Union (T
1 , T
2 ) - o (m log (N/M) uchun o'rtacha
ikkita daraxtni birlashtiradi, chunki barcha elementlar boshqacha (biroq, bu
operatsiya bir xil asimptotika bilan amalga oshirilishi mumkin, agar birlashganda
takroriy elementlarni olib tashlash kerak bo'lsa).
 Intersect (T
1 , T
2 ) - o (m log (N/M) uchun o'rtacha
ikkita daraxtning kesishgan qismini topadi (ya'ni ularning umumiy elementlari). Bu
erda ushbu operatsiyani amalga oshirish ko'rib chiqilmaydi.
Bundan tashqari, Dekart daraxti va uning qiymatlari bo'yicha ikki tomonlama
qidiruv daraxti bo'lgani sababli, k-th elementini topish va aksincha, element
raqamini aniqlash kabi operatsiyalar qo'llaniladi.
Amalga oshirish tavsifi
Amalga oshirish nuqtai nazaridan, har bir element X, Y va chap L va o'ng r o'g'liga
ishora qiladi.
Operatsiyalarni amalga oshirish uchun ikkita yordamchi operatsiyani amalga
oshirish kerak bo'ladi: Split va birlashma.
Split (T, X) - t daraxtini l va R (qaytariladigan qiymat) ikkita daraxtga ajratadi,
Shuning uchun L x tugmachasidan kichikroq bo'lgan barcha elementlarni o'z ichiga

oladi va r barcha elementlarni o'z ichiga oladi, katta X. ushbu operatsiya o (log N)
uchun amalga oshiriladi. Uni amalga oshirish juda oddiy - aniq rekursiya.
Merge (T
1 , T
2 ) - ikkita podderev t
1 va T
2 ni birlashtiradi va bu yangi daraxtni
qaytaradi. Ushbu operatsiya O (log N) uchun ham amalga oshiriladi. T
1 va T
2 ning
tegishli tartibga ega bo'lgan taxminida ishlaydi(birinchi x ning barcha qiymatlari x
qiymatidan ikkinchi x qiymatidan kam). Shunday qilib, biz ularni yning
ustuvorliklari bo'yicha tartibni buzmaslik uchun ularni birlashtirishimiz kerak,
buning uchun biz ildiz sifatida Y ning ildiziga ega bo'lgan daraxtni tanlaymiz va
o'zimizni boshqa daraxtdan va tanlangan daraxtning tegishli o'g'lidan chaqiramiz.
Endi Insert (X, Y) ning amalga oshirilishi aniq . Birinchidan, biz daraxtga
tushamiz (x uchun odatiy ikkilik qidiruv daraxtida bo'lgani kabi), lekin birinchi
elementda to'xtab qolamiz, unda ustuvor ahamiyatga ega y dan kamroq edi. Endi
biz topgan elementdan Split (X) ni chaqiramiz (elementdan barcha podderev bilan
birga) va L va R tomonidan qaytarilgan element qo'shilgan elementning chap va
o'ng o'g'li sifatida yoziladi.
Erase (X) ning amalga oshirilishi ham tushunarli . Biz daraxtga tushamiz (x
tomonidan odatiy ikkilik qidiruv daraxtida bo'lgani kabi), olib tashlangan
elementni qidiramiz. Elementni topib, biz faqat uning chap va o'ng o'g'illarini
birlashtiramiz va uning qiymatini olib tashlangan elementning o'rniga qo'yamiz.
Build operatsiyasi o (n log N) uchun ketma-ket Insert chaqiruvlari orqali amalga
oshiriladi.
Nihoyat, Union operatsiyasi (T
1 , T
2 ) . Nazariy jihatdan, uning asimptotikasi O (m
log (N / M)), lekin amalda u juda yaxshi ishlaydi, ehtimol juda kichik yashirin
sobit.
1 ->Y > T > >
2 ->Y, ya'ni ildiz t>
1 natijaning ildizidir. Natijani olish uchun t
1 -
>l, T>
1 ->r va T>
2 daraxtlarini ikkita daraxtga birlashtirishi kerak , shunda t 1
o'g'illari bo'lishi mumkin. Buning uchun biz split (T
2 , T
1 ->X) ni chaqiramiz,
Shuning uchun biz T>
2 ni L va R ning ikkita yarmiga ajratamiz, keyin t 1 o'g'illari
bilan birlashamiz: Union (T
1 ->L, L) va Union (t >
1 ->R, R), shuning uchun
natijaning chap va o'ng pastki qismini quramiz.
Amalga oshirish
Yuqorida tavsiflangan barcha operatsiyalarni amalga oshiramiz. Bu erda qulaylik
uchun boshqa belgilar joriy etildi-ustuvorlik prior, qiymatlar-kalit.

struct item {

int key, prior;

item * l, * r;

item() { }

item (int key, int prior) : key(key), prior(prior), l(NULL),
r(NULL)
{ }
};
typedef
item * pitem;
void
split (pitem t, int key, pitem & l, pitem & r) {

if (!t)

l = r = NULL;

else if (key < t->key)

split (t->l, key, l, t->l), r = t;

else

split (t->r, key, t->r, r), l = t;
}
void
insert (pitem & t, pitem it) {

if (!t)

t = it;

else if (it->prior > t->prior)

split (t, it->key, it->l, it->r), t = it;

else

insert (it->key < t->key ? t->l : t->r, it);
}
void
merge (pitem & t, pitem l, pitem r) {

if (!l || !r)

t = l ? l : r;

else if (l->prior > r->prior)

merge (l->r, l->r, r), t = l;

else

merge (r->l, l, r->l), t = r;
}
void
erase (pitem & t, int key) {

if (t->key == key)

merge (t, t->l, t->r);

else

erase (key < t->key ? t->l : t->r, key);
}
pitem
unite (pitem l, pitem r) {

if (!l || !r) return l ? l : r;

if (l->prior < r->prior) swap (l, r);

pitem lt, rt;

split (r, l->key, lt, rt);

l->l = unite (l->l, lt);

l->r = unite (l->r, rt);

return l;
}

Dekart daraxtini C va C++ tilida kodlash
Amalga oshirish
Yuqorida tavsiflangan barcha operatsiyalarni amalga oshiramiz. Bu erda qulaylik
uchun boshqa belgilar joriy etildi-ustuvorlik prior, qiymatlar-kalit .
struct item {

int key, prior;

item * l, * r;

item() { }

item (int key, int prior) : key(key), prior(prior), l(NULL),
r(NULL)
{ }
};
typedef
item * pitem;
void
split (pitem t, int key, pitem & l, pitem & r) {

if (!t)

l = r = NULL;

else if (key < t->key)

split (t->l, key, l, t->l), r = t;

else

split (t->r, key, t->r, r), l = t;
}
void
insert (pitem & t, pitem it) {

if (!t)

t = it;

else if (it->prior > t->prior)

split (t, it->key, it->l, it->r), t = it;

else

insert (it->key < t->key ? t->l : t->r, it);
}
void
merge (pitem & t, pitem l, pitem r) {

if (!l || !r)

t = l ? l : r;

else if (l->prior > r->prior)

merge (l->r, l->r, r), t = l;

else

merge (r->l, l, r->l), t = r;
}
void
erase (pitem & t, int key) {

if (t->key == key)

merge (t, t->l, t->r);

else

erase (key < t->key ? t->l : t->r, key);
}
pitem
unite (pitem l, pitem r) {

$if (!l || !r) return l ? l : r; if (l->prior < r->prior) swap (l, r); pitem lt, rt; split (r, l->key, lt, rt); l->l = unite (l->l, lt); l->r = unite (l->r, rt); return l; } Soxta o'lchamlarni qo'llab-quvvatlash Kartezyen daraxtining funksionalligini kengaytirish uchun, har bir tepalik uchun, uning pastki qismida - item tarkibida int CNT maydonini saqlash kerak. Misol uchun, u (log N) k-th yirik daraxt elementi ortida topish oson bo'ladi, yoki aksincha, bir xil asimptotika uchun tartiblangan ro'yxatda element sonini bilish (bu operatsiyalar amalga oshirish an'anaviy ikkilik qidiruv daraxtlar uchun ularning amalga oshirish farq qilmaydi). Daraxt o'zgarganda (elementni qo'shish yoki olib tashlash va h.k.) tegishli ravishda o'zgarishi kerak va ba'zi vertices cnt. Biz ikkita funktsiyani amalga oshiramiz - CNT() funktsiyasi CNT yoki 0 ning hozirgi qiymatini qaytaradi, agar Vertex mavjud bo'lmasa va upd_cnt () funktsiyasi CNT qiymatini ushbu Vertex uchun yangilaydi, agar uning o'g'illari l va r uchun bu cnt allaqachon to'g'ri yangilangan bo'lsa. So'ngra, tushunarli, faqat vazifalari upd_cnt qo'ng'iroqlarni kiritish uchun () har bir vazifalari oxirida insert, yo'q qilish, split, birlashtirish, doimiy CNT to'g'ri qadriyatlarni saqlab qolish uchun. int cnt (pitem t) { return t ? t->cnt : 0; } void upd_cnt (pitem t) { if (t) t->cnt = 1 + cnt(t->l) + cnt (t->r); } O (N ) uchun Kartezyen daraxtini oflayn rejimda qurish TODO Yopiq Dekart daraxtlari Yopiq Dekart daraxti odatiy Dekart daraxtining oddiy modifikatsiyasi bo'lib, u juda kuchli ma'lumotlar tuzilishi bo'lib chiqadi. Aslida, yopiq Dekart daraxti quyidagi operatsiyalarni amalga oshirish mumkin bo'lgan qator sifatida qabul qilinishi mumkin (barcha o (log n) onlayn rejimida):  Har qanday holatda bir qator ob'ektni joylashtiring  Tasodifiy elementni olib tashlash  Miqdori, tasodifiy segmentda minimal/maksimal va boshqalar.  Qo'shish, segmentdagi rasm  Segmentda to'ntarish (elementlarni teskari tartibda almashtirish)$ $Asosiy g'oya shundan iboratki, kalit sifatida elementlarning indekslarini ketma- ketlikda ishlatish kerak. Biroq, biz bu kalit qiymatlarini aniq saqlamaymiz (aks holda, masalan, elementni kiritishda daraxtning tepasida o (N) tugmachasini o'zgartirish kerak bo'ladi). Aslida, bu holatda, ba'zi bir tepalik uchun kalit, undan kichikroq bo'lgan vertices soni. Shuni ta'kidlash kerakki, undan kichikroq tepaliklar nafaqat chap podderevda, balki, ehtimol, ota-bobolarining chap burchagida ham. Keyinchalik aniqki, t ning ba'zi bir tepasi uchun yopiq kalit, bu tepalikning chap pastki qismida CNT(t->l) vertikalari soniga teng, shuningdek, bu tepalikning har bir ota-onasi uchun cnt(p - >l)+1 ning o'xshash qiymatlari, t p uchun o'ng pastki burchakda. Shubhasiz, hozirgi ustun uchun uning yopiq kalitini tezda qanday hisoblash mumkin. Barcha operatsiyalarda biz daraxtdan pastga tushib, har qanday tepaga etib boramiz, biz uning vazifalarini bajarish orqali bu miqdorni to'plashimiz mumkin. Agar biz chap tomonga boradigan bo'lsak, to'plangan mablag ' o'zgarmaydi va agar biz o'ng tomonga ketsak, CNT(t - >l)+1 bilan ortadi. Split va merge xususiyatlarining yangi ilovalarini taqdim etamiz: void merge (pitem & t, pitem l, pitem r) { if (!l || !r) t = l ? l : r; else if (l->prior > r->prior) merge (l->r, l->r, r), t = l; else merge (r->l, l, r->l), t = r; upd_cnt (t); } void split (pitem t, pitem & l, pitem & r, int key, int add = 0) { if (!t) return void( l = r = 0 ); int cur_key = qo'shish + cnt (t- > l); / / yopiq kalitni hisoblang if (key <= cur_key) split (t->l, l, t->l, key, add), r = t; else split (t->r, t->r, r, key, add + 1 + cnt(t->l)), l = t; upd_cnt (t); } Keling, yopiq daraxtlardagi turli xil qo'shimcha operatsiyalarni amalga oshirishga o'taylik:  Elementni kiritish. Pos holatiga elementni kiritishimiz kerak. Dekartovo daraxtini ikki qismga ajratamiz: massivga mos keladigan [0..pos-1] va qator [pos..sz]; buning uchun split (t, t1, t2, pos) ni chaqirish kifoya. Shundan so'ng biz T1 daraxtini yangi tepalik bilan birlashtira olamiz; buning uchun merge (t1, t1,$ $new_item) ni chaqirish kifoya (merge uchun barcha shart-sharoitlar bajarilganligiga ishonch hosil qilish qiyin emas). Nihoyat, ikkita T1 va t2 daraxtlarini t - Challenge merge (t, t1, t2) daraxtiga birlashtiramiz.  Elementni olib tashlash. Bu erda hali ham osonroq: olib tashlanadigan elementni topish va keyin uning o'g'illari l va r uchun birlashma qilish va birlashma natijasini t ning yuqori qismiga qo'yish kifoya.  Miqdori / minimal va h.k. segmentda. Birinchidan, har bir tepalik uchun, biz ushbu yuqori qismini podderev uchun maqsadli funktsiyaning qiymatini saqlaydigan item tarkibida qo'shimcha f maydonini yaratamiz. Bu maydon qo'llab-quvvatlash cnt registri o'xshash, albatta, kerak, saqlab qolish uchun oson (bu maydon qiymatini hisoblash vazifasini yaratish, o'g'illari uchun uning qadriyatlarini foydalanib, va daraxtni o'zgartirish, barcha funktsiyalari oxirida bu vazifani kiritish). Ikkinchidan, so'rovga o'zboshimchalik bilan javob berishni o'rganishimiz kerak [A; B]. Daraxtdan uning qismini [A;B] segmentiga mos ravishda ajratishni o'rganamiz. Bu birinchi navbatda split (t, t1, t2, a) va keyin split (t2, t2, T3, B-a+1) ni chaqirish uchun etarli ekanligini tushunish qiyin emas. Natijada, t2 daraxti va segmentdagi barcha elementlardan iborat bo'ladi [A; B], va faqat ular. Shuning uchun so'rovga javob t2 ning yuqori qismidagi f maydonida bo'ladi. So'rovga javob bergandan so'ng, daraxt birlashma (t, t1, t2) va birlashma (t, t, t3) chaqiruvlari bilan tiklanishi kerak.  Segmentga qo'shish/bo'yash . Bu erda biz oldingi nuqtaga o'xshash harakat qilamiz, lekin f maydonining o'rniga Add maydonini saqlaymiz, bu esa qo'shilgan qiymatni (yoki bu tepalikning barcha bo'yoqlarini bo'yab turadigan qiymatni) o'z ichiga oladi. Har qanday operatsiyani bajarishdan oldin, ushbu add qiymati "surish" kerak, ya'ni t - l->add va t->>r->>>add-ni mos ravishda o'zgartiring va Add qiymatini olib tashlang. Shunday qilib, daraxtning hech qanday o'zgarishi bilan ma'lumot yo'qolmasligiga erishamiz.  Segmentdagi inqilob. Ushbu element oldingi holatga deyarli o'xshaydi-siz bool rev maydonini kiritishingiz kerak, bu esa hozirgi tepalikning pastki qismida inqilob qilishni talab qilganda haqiqiydir. Rev maydonining "itarilishi" biz hozirgi tepalikning o'g'illarini almashtiramiz va ular uchun bu bayroqni qo'yamiz. Amalga oshirish. Misol uchun, segmentdagi to'ntarish bilan bevosita Dekart daraxtining to'liq amalga oshirilishi. Bu erda har bir tepalik uchun qiymat maydoni ham saqlanadi-elementning haqiqiy qiymati, joriy holatdagi qatorda turgan. Bundan tashqari, Output () funktsiyasining amalga oshirilishi ham mavjud bo'lib, unda bevosita Dekart daraxtining hozirgi holatiga mos keladigan qator chiqariladi. 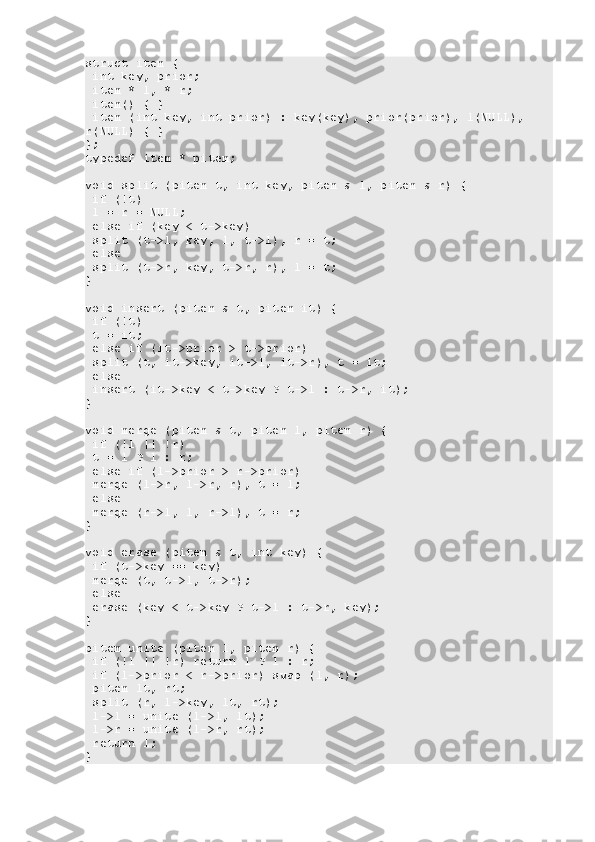typedef struct item * pitem; struct item { int prior, value, cnt;$ $bool rev; pitem l, r; }; int cnt (pitem it) { return it ? it->cnt : 0; } void upd_cnt (pitem it) { if (it) it->cnt = cnt(it->l) + cnt(it->r) + 1; } void push (pitem it) { if (it && it->rev) { it->rev = false; swap (it->l, it->r); if (it->l) it->l->rev ^= true; if (it->r) it->r->rev ^= true; } } void merge (pitem & t, pitem l, pitem r) { push (l); push (r); if (!l || !r) t = l ? l : r; else if (l->prior > r->prior) merge (l->r, l->r, r), t = l; else merge (r->l, l, r->l), t = r; upd_cnt (t); } void split (pitem t, pitem & l, pitem & r, int key, int add = 0) { if (!t) return void( l = r = 0 ); push (t); int cur_key = add + cnt(t->l); if (key <= cur_key) split (t->l, l, t->l, key, add), r = t; else split (t->r, t->r, r, key, add + 1 + cnt(t->l)), l = t; upd_cnt (t); } void reverse (pitem t, int l, int r) { pitem t1, t2, t3; split (t, t1, t2, l); split (t2, t2, t3, r-l+1); t2->rev ^= true; merge (t, t1, t2);$

merge (t, t, t3);
}
void
output (pitem t) {

if (!t) return;

push (t);

output (t->l);

printf ("%d ", t->value);

output (t->r);
}

FOYDALANILGAN ADABIYOTLAR
1. Thomas H. Cormen va b. Intruduction to algorithms. Massachusetts
Institute of Technology. London 2009.
2. Robert Sedgewick and Kevin Wayne. Algorithms. FOURTH
EDITION. Princeton University. First printing, March 2011.
3. В.Д.Колдаев. Основы алгоритмизации и программирования.
Учебное пособие, Москва ИД “Форум”- ИНФРА-М 2006 г.
4. Фаронов В. В. Turbo Pascal. — СПб.: ВХВ- Санкт-
11етербург, 2004. - 1056 с.

5. Слинкин Д.А.Основы программирования на Турбо-Паскаль:
Учебно-методическое пособие для студентов вузов. Шадринск:
Изд-во Шадринского пединститута, 2003. - 244 s.
6. Michael Van Canneyt. Free Pascal Reference guide. Reference
guide for Free Pascal, version 3.0.0. Document version 3.0 November
2015. Pp 11-13, 20-21, 25, 28, 30, 159.
7. Marco Cantu. Essential Pascal. Piacenza, Italy 4th Edition, April
2008. Pp 26, 30-35.
8. Motaz Abdel Azeem. Start Programming using Object Pascal.
Edited by: Pat Anderson, Jason Hackney -28 September, 2013y. Pp 18.
9. M.U.Ashurov, N.D.Mirzaxmedova. Turbo Pascal dasturlash
tili.(uslubiy qo‘llanma),Toshkent TDPU - 2011.
10. Adam Drozdek. Data structures and algorithms in C++. Secoedition. 2001 by
Brooks/ Cole.
11. Narzullaev U.X., Qarshiev A.B., Boynazarov I.M. Ma’lumotlar tuzilmasi va
algoritmlar. //O’quv qo’llanma. Toshkent: Tafakkur nashriyoti, 2013 y. – 192 b.
Xulosa
Men berilgan mavzu bo’yicha yetarlicha bilim va ko’nikmalarga ega bo’ldim.
Bu mavzuda daraxt , ikkilik daraxt , dekart daraxti haqida ma’lumotlarga ega
bo’ldim . Dekart daraxti bu – koordinatalar sistemasida berilgan daraxtdir. Uning
daraxtdan faqri koordinatalar sistemasi orqali uchning koordinata nuqtasi ,
joylashish o’rnini , qirraning esa berilgan uch koordinatalari orqali uning
uzunligini aniqlash mumkin. Bu mavzuda daxaxtlarni Prufer kodi yordamida
tiklash va ularni qayta qurishni o’rgandim.. Algoritmlarning bahosi algoritmni vaqt
va xotira hajmiga nisbatan olinadi. Vaqt va xotira hajmi qancha kam bo’lsa,

algoritm bahosi shunchalik yaxshi bo’ladi. Ammo saralash uchun berilgan ketma
ketlikga ham qisman bog’liq bo’ladi. Masalan: A){1,2,3,4,5,6,7,8} sonlarni ketma-
ket kamayish tartibida yozing, va B){1,2,3,4,5,6,7,8} sonlarni ketma ket o’sish
tartibida yozing , yuqoridagi A va B misollarda B misolni bahosi yaxshi
hisoblanadi ,chunki B masala shartga ko’ra o’sish tartibida joylashgan .Piramidali
saralash odatda uyum yoki g’aram saralashi deb ham yuritiladi.Ushbu saralash
usulida shartga asosan eng katta (eng kichik) sonlar yuqoriga chiqadi.. Piramidali
saralsh algoritmining boshqa algoritmlardan farqi :xotira hajmi borgan sari
kamayib boradi .
Men kurs ishimni bajarishda algoritmlar ,ularni baholash, algoritmlar tarixi haqida
o’rganib oldim. Ulardan tashqari word dasturi bilan ishlashni ham o’rganib oldim.
Hozirgi kunda saralash algoritmlari hayotda juda ham ko’p ishlatilayabdi.
Masalan:Oliy ta’limga kirish uchun abituryentlar imtihon topshirishadi ,bizga
berilayotgan imkoniyatlar bilan har bir talaba 5 ta OTMga imtihon topshirishlari
mumkun.Bu jarayonda talabalarni aniqlash uchun abituryentlarni ballari saralanadi.
Bundan tashqari hozirgi kunda pandimiya sharoyitida emlash jarayonlari
ketayabdi. Har bir fuqarolar avval shaxr keyin tuman so’ngra MFY(QFY)lar
bo’yicha saralanadi.So’ngra har bir maxallalar ichida familyasi bosh harfi bilan
saralanadi.Bu saralash jarayonni yanada tezlashtiradi va bir qancha qulayliklar
yaratadi.

DEKART DARAXTI (TREAP, DERAMID) Mundarija: 1.Kurs ishi uchun qo’yilgan mavzu……………………2 2.Kirish………………………………………………...4 3.Asosiy qism………………………………………….6 5.Xulosa……………………………………………….23 4.Foydalanilgan manba va adabiyotlar ro’yxati………24

Reja: Kirish 1.Daraxt tushunchasi. * Daraxt va unga ekvivalent tushunchalar * Ikkilik daraxt * Daraxtlarni Prufer kodida kodlash 2.Dekart daraxti . * Dekart daraxti haqida tushuncha. * Dekart daraxtini C va C++ tilida kodlash. 3.Xulosa 4.Foydalanilgan adabiyotlar ro’yxati

Kirish: Algoritm kibernetika va matematikaning asosiy tushunchalaridan biri bo'lib, bu atama o'rta asrlarda yashab ijod etgan buyuk o'zbek matematigi Al-Xorazmiy nomidan kelib chiqqan. U IX asrning 825 yilidayoq o'zi kashf etgan o'nli sanoq tizimida to‘rt arifmetika amallarini bajarish qoidalarini bergan. Arifmetika amallarini bajarish jarayoni esa al-xorazm deb atalgan. Bu atama 1747 yildan boshlab algorismus, 1950 yilga kelib algorifm deb ham ataldi. Fanda "Yevklid algoritmi", "G'iyosiddin Koshiy algoritmi", "Laure algoritmi", "Markov algoritmi" deb ataluvchi algoritmlar ma’lum algoritm tushunchasi tobora kengayib borib, kibernetikaning nazariy va mantiqiy asosi hisoblangan algoritmlar nazariyasi paydo bo'lgan. Kompyuterlar paydo bo'lishi bilan algoritm atamasi hozirgi ma'nosi bilan axborot texnologiyalari sohasida eng asosiy atamalardan biri bo'lib qoldi. Odatda algoritmlar u yoki bu hisoblashga doir masalalarni (computational problems) yechish uchun tuziladi. Qo'yilgan masala ushun yaratiladigan algoritmda kiruvchi va chiquvchi ma’lumotlar muhim ahamiyatga ega, agar algoritm to'g'ri tuzilgan bo'Isa, ijrosi (kompyuter) aniq natijalar beradi. Algoritm quyidagi xossalarga ega: aniqlilik, tushunarlilik, ommaviylik, natijaviylik va diskretlik. Aniqlik va tushunarlilik - deganda, algoritmda ijrochiga berilayotgan ko'rsatmalar aniq mazmunda bo'lishi tushuniladi. Chunki ko'rsatmalardagi noaniqliklar mo'ljallangan maqsadga erishishga olib keimaydi. Ijrochiga tavsiya etiladigan ko'rsatmalar 8 tushunarli mazmunda bo‘lishi shart, aks holda ijrochi uni bajara olmaydi. Ommavivlik - deganda, har bir algoritm mazmuniga ko‘ra bir turdagi masalalaring barchasi uchun ham o‘rinli bo‘lishi,ya’ni umumiy bo‘lishi tushuniladi. Natiiaviylik - deganda, algoritmda chekli qadamlardan so‘ng albatta natija bo’lishi tushuniladi. Shuni ta'kidlash joizki, algoritm avvaldan ko‘zlangan maqsadga

erishishga olib kelmasligi ham mumkin. Bunga ba'zan algoritmning noto‘g‘ri tuzilgani yoki boshqa xatolik sabab bo‘lishi mumkin, ikkinchi tomondan, qo‘yilgan masala ijodiy yeshimga ega bolmasligi ham mumkin. Lekin salbiy natija ham deb qabul qilinadi. Diskretlik - deganda, algoritmlami chekli qadamlardan tashkil qilib bo'laklash imkoniyati tushuniladi. Algoritmlarga doir quyidagi masalalarini misol sifatida keltirish mumkin: • Talabani kundalik ishlarini tashkil etish; • To‘rtburchak perimetri va yuzasini hisoblash; • R radiusli doira yuzasini va aylana uzunligini topish; • A1, A2 , А 3,..., An sonlarni toq elementlarini yig‘indisini topish; • Berilgan ketma-ketlik sonlarni o‘sish (kamayish) tartibda joylashtirish va h.k. Algoritm ning uchta turi mavjud: chiziqli, tarmoqlanuvchi va takrorlanuvchi(siklik). Chiziqli algoritmlar - hech qanday shartsiz faqat ketma-ket bajariladigan jarayonlardir. Tarmoqlanuvchi algoritmlar - ma’lum shartlarga muvofiq bajariladigan jarayonlardir. Takrorlanuvchi algoritmlar - biron-bir shart tekshirilishi yoki biron parametming har xil qiymatlari asosida chekli ravishda takrorlanish yuz beradigan jarayonlardir.

Daraxt tushunchasi . * Daraxt va unga ekvivalent tushunchalar . Daraxt (grafik nazariyasi) - Tree (graph theory) Daraxtlar 6 ta vertikal va 5 ta qirrali etiketli daraxt . Vertices v Qirralar v − 1 Xromatik raqam 2 agar v > 1 Grafiklar va parametrlar jadvali D araxt bu yo'naltirilmagan grafik unda har qanday ikkitasi tepaliklar bilan bog'langan to'liq bitta yo'l yoki unga teng ravishda a ulangan asiklik yo'naltirilmagan grafik. A o'rmon har qanday ikkita tepalik ulangan yo'naltirilmagan grafik ko'pi bilan yo'l, yoki ekvivalent ravishda asiklik yo'naltirilmagan grafik yoki ekvivalent ravishda a uyushmagan birlashma daraxtlar. A polytree (yoki yo'naltirilgan daraxt yoki yo'naltirilgan daraxt yoki yakka o'zi ulangan tarmoq ) a yo'naltirilgan asiklik grafik (DAG) asosiy yo'naltirilmagan grafasi daraxtdir. A polyforest (yoki yo'naltirilgan o'rmon yoki yo'naltirilgan o'rmon ) bu yo'naltirilgan asiklik grafik, uning ostida yo'naltirilmagan grafasi o'rmondir.

DEKART DARAXTI (TREAP, DERAMID)

12.08.2023

0

249.171875 KB

Похожие