Fenvik daraxti


![operatsiyasini qo'llab-quvvatlaydi. Daraxtdagi minimalni qayta hisoblash
prefiksdagi minimum massivini yangilashdan ko'ra tezroq.
1.Fenvik daraxti va uning ishlash prinsipi
Fenvik daraxti-bu ma'lumotlar tuzilishi, massivdagi daraxt, quyidagi
xususiyatlarga ega:
1) O (log N) vaqtidagi har qanday [L; R] segmentidagi ba'zi qaytariladigan g
operatsiyasining qiymatini hisoblash imkonini beradi;
2)har qanday elementning qiymatini O (log N) ga o'zgartirishga imkon beradi;
3) O (N) xotirani talab qiladi, aniqrog'i N elementlar qatori bilan bir xil;
4) Ko'p o'lchovli massivlar uchun osongina umumlashtiriladi. Fenvik daraxtining
eng keng tarqalgan ishlatilishi segmentdagi yig'indini hisoblashdir, ya'ni funktsiya
G (X1,..., Xk) = X1 + ... + Xk. Fenvik daraxti birinchi marta "a new data structure
for cumulative frequency tables" (Peter M. Fenwick, 1994) maqolasi bilan
tasvirlangan.
Sum funktsiyasi a qatorining barcha elementlari bo'ylab harakatlanadigan
joyga t qatori bo'ylab harakatlanib, iloji boricha segmentlar bo'ylab "sakrash" ni
amalga oshiradi. Birinchidan, u [F(R); R] segmentidagi summaning qiymatini
javobga qo'shadi, so'ngra [F(F(R)-1); F(R)-1] segmentidagi summani oladi va
hokazo nolga yetguncha. Upd funktsiyasi teskari yo'nalishda - indekslarni
ko'paytirish tomon siljiydi, TJ yig'indisi qiymatlarini faqat kerakli pozitsiyalar
uchun yangilaydi, ya'ni f(j) <= i <= j bo'lgan barcha j uchun. shubhasiz, ikkala
operatsiyaning tezligi F funktsiyasini tanlashga bog'liq bo'ladi. F(X) qiymatini
quyidagicha aniqlaymiz:
3](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_3.png)
![F(X) = X & (X+1) (1)
F(j) ni topish < = i < = j formulaga mos keladi:
H(X) = X / (X+1) (2)
1.1. Operatsiya F. F operatsiyasini turli yo'llar bilan tanlash mumkin, lekin
ko'pincha interval yig'indisi operatsiyalari, interval mahsuloti, shuningdek ma'lum
bir modifikatsiya va cheklovlar, intervalda maksimal va minimalni topish yoki
boshqa operatsiyalar olinadi.
Eng oddiy vazifa Massivning ketma-ket elementlari yig'indisini topish
muammosini ko'rib chiqing. Ko'p so'rovlar bo'lishini hisobga olsak, s (L, R) ni
topishingiz kerak bo'lgan shakl (L,R)- a[L] dan a[R] gacha bo'lgan barcha
elementlarning yig'indisi. Ushbu muammoning eng oddiy echimi qisman
summalarni topish bo'ladi. Ularni topgandan so'ng, biz ushbu summalarni
sum[i]=a[1]+a[2]...+a[i]. bo'lgan qatorga yozamiz...+ a[i]. Keyin so'rovda talab
qilinadigan qiymat S(L,R)=sum[R]-sum[L-1] (sum[0] odatda alohida holatlarni
hisobga olmaslik uchun nolga teng deb hisoblanadi).
Kamchiliklari - ushbu vazifani amalga oshirishda muhim kamchiliklar
mavjud. Va asosiylaridan biri shundaki, asl massivning bitta elementini
o'zgartirganda, o'rtacha O(N) qisman summalarni qayta hisoblash kerak va bu vaqt
talab etadi. Ushbu muammoni hal qilish uchun siz Fenvik daraxtidan
foydalanishingiz mumkin.
Afzalliklari - Ushbu dizaynning asosiy afzalligi-amalga oshirish qulayligi va
so'rovlarga javoblarning tezligi O (1).
Fenvik daraxtining ushbu vazifa uchun qo'llanilishi. Tabiiy sonlarda
aniqlangan va x&(x+1) (&- bit va) ga teng bo'lgan g (x) funktsiyasini kiritamiz.
Shunday qilib, g (x) x ga teng, agar x ning ikkilik kengayishida oxirgi 0 bo'lsa (x 2
ga bo'linadi). Va agar ikkilik kengayishda x kichik raqamlarda birliklar guruhi
mavjud bo'lsa, unda funktsiya x ga teng bo'lib, oxirgi birliklar 0 ga almashtiriladi.
Bu x & (x+1) ekanligiga misollar bilan ishonch hosil qilishingiz mumkin.
4](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_4.png)
![Endi biz quyidagi qisman summalarni hisoblaymiz va ularni
t[i] = a[G[i]] + a[G[i]+1]…+ a[i] ga yozamiz. Keyinchalik, ushbu summalarni
qanday topish mumkinligi ko'rsatiladi.
1.2. Miqdorni hisoblash. S(L,R) ni topish uchun s(1, L-1) va s(1,R) ni
qidiramiz. Agar t qatori bo'lsa, s(L, R) ni topadigan funktsiyani yozamiz. Bunday
holda, chap uchi summaga kiritilmaydi, lekin uni yoqish oson agar bu vazifada
talab qilinsa (kodga qarang).
const int N = 100;
int t[N],a[N];
int sum(int L, int R)
{
int res=0;
while (R >= 0) {
res += t[R];
R = G( R ) - 1;
}
while (L >= 0) {
res -= t[L];
L = G(L) - 1;
}
return res;
}
Shuni ham ta'kidlash kerakki, har bir dastur uchun g funktsiyasi x ikkilik
yozuvidagi birliklar sonini kamida 1 ga kamaytiradi. Shundan kelib chiqadiki,
summani hisoblash O (log N) uchun amalga oshiriladi.
Elementlarni o'zgartirish. Endi elementlarning modifikatsiyasini ko'rib
chiqing. Elementlarning qanday o'zgarishiga qarab qisman summalarni tezda
5](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_5.png)
![o'zgartirishni o'rganishimiz kerak. Keyin biz massiv elementlarini o'zgartirishimiz
kerak t[j], buning uchun tengsizlik to'g'ri G(j)<k<j. ammo keyin keyingi hiyla
yordamga keladi. Barcha kerakli jlar k[i] ketma-ketligiga tegishli bo'ladi (hisob-
kitobga qarang).
(3)
Bu | belgi o’rnida yoki tushuniladi.
Shuni ta'kidlash kerakki, bu funktsiya qat'iy ravishda o'sib boradi va eng
yomon holatda logaritma marta qo'llaniladi, chunki u har safar k sonining ikkilik
kengayishida bitta birlikni qo'shadi. a[ k ] elementini d ga o ' zgartiradigan va shu
bilan birga tegishli qisman summalarni o ' zgartiradigan funktsiyani yozamiz .
const int N=100;
int t[N],a[N];
void upd(int k, int d)
{
a[k]+=d;
while(k<N)
{
t[k]+=d;
k=(k|(k+1));
}
}
Ishga tushirish Endi biz t qatorini dastlabki hisoblashda uni nol bilan
boshlash mumkinligini ta'kidlaymiz. Shundan so'ng,biz n elementlarning har biri
uchun upd(i, a[i]) funktsiyasidan foydalanamiz. Keyin dastlabki hisoblash
6](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_6.png)




![2.Dasturlash tillarida amalga oshirish
2.1. C dasturlash tilida amalga oshirish
// Hajmi 1 + 2 quvvat bo'lishi kerak.
int A[SIZE];
// 1 qiymatiga ega bo'lgan i ning eng kam ahamiyatli biti
#define LSB(i) ((i) & -(i))
// Birinchi i elementlar summasini qaytaradi (ko'rsatkichlar 0 i uchun)
// Range_sum teng (0, i)
int prefix_sum(int i) {
int sum = A[0];
for (; i != 0; i -= LSB(i))
sum += A[i];
return sum;
}
// i indeksli elementga delta qo'shing (nolga asoslangan)
void add(int i, int delta) {
if (i == 0) {
A[0] += delta;
return;
11](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_11.png)
![}
for (; i < SIZE; i+= LSB(i))
A[i] += delta;
}
C ning foydali funksiyalari.
// Elementlar yig'indisini i + 1 dan j gacha qaytaradi
// Prefiks_sum(j) ga teng - prefiks_sum(i), lekin biroz tezroq
int range_sum(int i, int j) {
int sum = 0;
for (; j > i; j -= LSB(j))
sum += A[j];
for (; i > j; i -= LSB(i))
sum -= A[i];
return sum;
}
// A[ ] Joyini Fenvik daraxti shakliga aylantiring
void init(void) {
for (int i = 1; i < SIZE; ++i) {
int j = i + LSB(i);
if (j < SIZE)
A[j] += A[i];
}
}
// Boshiga-element soni qator qaytib aylantirish
12](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_12.png)
![void fini(void) {
for (int i = SIZE - 1; i > 0; --i) {
int j = i + LSB(i);
if (j < SIZE)
A[j] -= A[i];
}
}
// Bitta element qiymatini qaytaring
int get(int i) {
return range_sum(i, i + 1);
}
// Set (rostlash farqli o'laroq) bitta elementning qiymati
void set(int i, int value) {
add(i, value - get(i));
}
// Prefix_sum(i) bilan eng katta i ni toping <= qiymat.
// Eslatma: barcha qiymatlar manfiy bo'lmagan bo'lishini talab qiladi!
unsigned int rank_query(int value) {
int i = 0, j = SIZE - 1;
// j is a power of 2.
value -= A[0];
for (; j > 0; j >>= 1) {
if (i + j < SIZE && A[i + j] <= value) {
value -= A[i + j];
i += j;
}
13](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_13.png)
![}
return i;
}
2.2. C ++ dasturlash tilida amalga oshirish
class FenwickTree {
private:
vector<int> data;
int getParent(int i) const {
return i - (i & (-i));
}
int getNext(int i) const {
return i + (i & (-i));
}
public:
FenwickTree(int n) : data(n+1, 0) {
}
int getSum(int i) const {
int sum = 0;
++i;
while (i > 0) {
sum += data[i];
i = getParent(i);
}
return sum;
14](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_14.png)
![}
void update(int i, int v) {
++i;
while (i < data.size()) {
data[i] += v;
i = getNext(i);
} }
}; mal
Fenwick Tree (shuningdek, Binary Indexed Tree nomi bilan ham tanilgan).
Python-da amalga oshirish:
2.3. Python dasturlash tilida amalga oshirish
class FenwickTree:
def __init__(self, n):
self.size = n
self.tree = [0] * (n + 1)
def update(self, index, value):
while index <= self.size:
self.tree[index] += value
index += index & -index
def query(self, index):
result = 0
while index > 0:
result += self.tree[index]
index -= index & -index
return result
15](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_15.png)
![def range_query(self, left, right):
return self.query(right) - self.query(left - 1)
2.4. Java dasturlash tilida amalga oshirish
class FenwickTree {
private int[] tree;
private int size;
public FenwickTree(int n) {
size = n;
tree = new int[n + 1];
}
public void update(int index, int value) {
while (index <= size) {
tree[index] += value;
index += index & -index;
}
}
public int query(int index) {
int result = 0;
while (index > 0) {
result += tree[index];
index -= index & -index;
16](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_16.png)

![3. Fenvik daraxtiga vizual kirish
Fenvik daraxti, shuningdek, ikkilik indekslangan daraxt deb ham ataladi, bu
elementlarni yangilash va massivlardagi diapazon so'rovlarini baholash uchun
ishlatiladigan ma'lumotlar strukturasidir. Ikkilik raqamlarni ikki o'lchamda
tartiblash usuli yordamida boshqa shunga o'xshash ma'lumotlar tuzilmalaridan farq
qiladi.
Uning oddiy amalga oshirilishi qanday va nima uchun ishlashini tushuntirib
beradigan ajoyib xususiyatlarni yashiradi. Ushbu maqola Fenvik daraxti nima
ekanligini, nima uchun uni 1 ga indeksatsiya qilish kerakligini, kichik ahamiyatga
ega bit yordamida daraxt bo'ylab qanday harakat qilishni va eng muhimi,
xususiyatlari sehrli ko'rinadigan ushbu tuzilish g'oyasi qanday paydo bo'lishi
mumkinligini vizual ravishda tushuntirishga harakat qiladi.
Diapazon summasini so'rash muammosi. Ma'lumotlar tuzilishi haqida
gapirishdan oldin, keling, u qanday muammoni hal qilmoqchi ekanligini tushunib
olaylik.
V qatorini hisobga olgan holda, biz ikkita operatsiyani taxmin qilishimiz
kerak:
So'rov (l, r): berilgan oraliqdagi barcha elementlarning yig'indisini toping
[l,r].
Yangilash (i, val): massivning i pozitsiyasining qiymatini val ga o'zgartiring.
Masalan, massiv uchun [-5, 7, 0, 1, 3, 2, -1, 0, 2], so'rov natijasi (1, 4) 11 ni
qaytarishi kerak. Ammo, agar biz yangilanishni(3, 5) chaqirsak va keyin query
18](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_18.png)
![qiymatini(1, 4) tekshirsak, natija 11 emas, 15 bo'ladi, chunki massiv endi
boshqacha. 1 (a, b, c) -Rasmga qarang.
1-a Rasm :
1 – a Rasmda so'rov (1, 4) bu 7+0+1+3=11.
1-b Rasm:
1 – b Rasmda 3-pozitsiyaning qiymati 5 ga aylanadi.
1-c Rasm :
1 – c Rasmda so'rov (1, 4) endi 7+0+5+3=15, 11 emas.
Sodda echim So'rovga javob berish uchun barcha elementlarning yig'indisini
to'plab, l pozitsiyasidan r pozitsiyasiga v orqali takrorlash kifoya. Yangilash uchun
i-pozitsiya v qiymatini o'zgartirish kifoya .
int
query(int
v[],int
l,int r) {
int s = 0;
19](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_19.png)
![for (int i = l; i <= r; i++) {
s += v[i];
}
return s;
}
void update(int v[], int i, int val) {
v[i] = val;
}
Ushbu strategiya so'rov O (|v|) da bajarilganligi sababli O (1) vaqtni
yangilashga imkon beradi.
Yana bir sodda echim Oldingi echim ortidagi mantiq teskari bo'lishi
mumkin.
U massiv prefikslari yig'indisidan foydalanadi. V massivining s[i] prefikslari
yig'indisi v[0] + v[1] + ga teng ... + v[i].
2-a Rasm. prefikslari yig'indisini qurish.
Yuqori qator - bu massiv V. pastki qator-prefikslarning yig'indisi V. Boshqa
tomondan, har bir yangilanishda, eng yomon stsenariyda, birinchi elementning
20](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_20.png)
![qiymatini O(|v|) murakkablik vaqti uchun prefikslar yig'indisining butun qatorini
qayta tiklash orqali o'zgartirishimiz kerak.
int
query(int
s[], int l,
int r) {
if (l == 0) return s[r];
else return s[r] - s[l - 1];
}
void update(int s[], int v[], int n, int i, int val) {
for (int j = i; j < n; j++) {
s[j] -= v[i];
s[j] += val;
}
v[i] = val;
}
Birinchi yechim yaxshi yangilanishga ega, ammo dahshatli so'rov.
Ikkinchisida yaxshi so'rov bor, ammo dahshatli yangilanish. Hozir qilish kerak
bo'lgan tabiiy narsa, so'rov ham, yangilanish ham tez yoki sekin bajarilmaydigan
yechim bor - yo'qligini so'rashdir.
Misollar:
21](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_21.png)
![1. Miqdor o'rniga bizga massivning [l, r] diapazonidagi minimal element kerak.
Buning uchun biz hali ham ikkinchi algoritmdan foydalana olamizmi? So'rovni o
(1) vaqt murakkabligi bilan bajarish uchun nimani o'zgartirishimiz kerak?
3.1. Fenvik Daraxti . Fenvik daraxti prefiks summasining ishlashini
yaxshilaydi, lekin u diapazon summasini so'rash muammosini aniq hal qilmaydi.
Uning ba'zi cheklovlari bor. Ushbu tuzilma ikki xil operatsiyani baholashi
mumkin:
1. so'rov (n): birinchi n elementlarning yig'indisini toping.
2. qo'shish (i, val): massivning i pozitsiyasining qiymatiga val qiymatini
qo'shing.
Ushbu operatsiyalarni biz xohlagan operatsiyalarga qanday o'zgartirishimiz
mumkinligini ko'rish oson.
Daraxt tushunchasi. Keling, oraliq ikkilik daraxtni shunday quramizki, uning
tugunlari massiv segmenti uchun javobni o'z ichiga oladi. Ildiz tuguni, ta'rifiga
ko'ra, butun massivning yig'indisini o'z ichiga oladi. Uning chap avlodi birinchi
yarmining yig'indisini, o'ng avlodi esa ikkinchi yarmining yig'indisini o'z ichiga
oladi.
Umuman olganda, har bir tugun massivning bitta segmentini, uning chap bolasi
ushbu segmentning birinchi yarmini, o'ng bolasi esa ikkinchi yarmini ifodalaydi.
22](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_22.png)



![int res = 0;
while (n > 0) {
res = op(res, fenwick[n]);
n -= lsb(n);
}
return res;
}
C ++da Fenvik daraxti so'rovini amalga oshirish. LSB makrosida berilgan
sonning eng kichik muhim biti hisoblanadi.
Ushbu ma'lumotlar tuzilishi Fenvik daraxti yoki ikkilik indekslangan daraxt deb
ataladi.
Yangilash operatsiyasini amalga oshirish biroz qiyinroq, ammo tushunish
osonroq. Oxirgi tugunning "yuqoridagi" barcha tugunlari uning yig'indisida oxirgi
tugunning qiymatini o'z ichiga oladi. Qiymatni yangilaganimizda, biz oxirgi
tugunning qiymatini o'zgartira boshlaymiz va uning "ustidagi" barcha tugunlarni
yangilaymiz.
E'tibor bering, b tugunining ajdodi bo'lgan a tuguni A ning B dan "yuqori"
ekanligini anglatmaydi.
26](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_26.png)

![Fenvik daraxtiga kirish. Prefix_sum qatoridan foydalanish. Misol:
8-Rasm: prefix_sum.
Agar biz a[0]+a [1]+...+ in [4] ni hisoblamoqchi bo'lsak, biz uni
hisoblashimiz shart emas buning o'rniga biz shunchaki qaytarishimiz mumkin
_prefix\_sum[4]_ chunki u allaqachon ushbu qiymatlarning yig'indisini o'z ichiga
oladi.
Bu shuni anglatadiki, biz barcha bunday so'rovlarga doimiy vaqtda javob
bera olamiz, lekin agar biz massiv elementlarini tez-tez yangilab turishimiz kerak
bo'lsa, prefix_sum massividan foydalanish foydasiz bo'ladi, chunki yangilanish
holatida biz butun prefix_sum massivini qayta qurishimiz kerak bo'lishi mumkin.
Bunday hollarda ikkilik indekslangan daraxt sahnaga chiqadi. Odatda Fenvik
daraxti deb nomlanuvchi ikkilik indekslangan daraxt-bu har bir tugundagi massiv
elementlarining kümülatif chastotalarini qo'llab-quvvatlaydigan ma'lumotlar
tuzilishi.
Eng yaxshi va eng oson foydalanish holatlaridan biri logaritmik vaqt
murakkabligining qiymatlari o'zgartirilishi mumkin bo'lgan (ya'ni qiymatlarni
o'zgartirish mumkin) massiv prefikslari yig'indisini hisoblash bo'lishi mumkin.
4.1. Fenvik daraxtining asosiy g'oyasi. Agar n hajmli a massivni
prefix_summasini hisoblashni istasak u holda biz boshqa massivdan foydalanamiz
(bit) hajmi n+1 (n+1 - oddiylik uchun 1 ga asoslangan indeksatsiyani saqlang).
Ikkilik indekslangan daraxtning asosiy g'oyasi shundaki, biz yangi hosil
bo'lgan massiv indeksi bo'yicha ma'lum bir element diapazonining yig'indisini
saqlashimiz mumkin
28](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_28.png)
![Fenvik daraxtini shakllantirishda "har bir butun son 2 daraja yig'indisi
sifatida ifodalanishi mumkin" degan fikr keng qo'llaniladi. Ushbu faktdan
foydalanib, logaritmik vaqt murakkabligi bilan massivning _prefix\_sum_ ni
hisoblashimiz mumkin.
Keling, misolni ko'rib chiqaylik: aytaylik, biz yig'indisi saqlanadigan qatorni
bilmoqchimiz byat [12], biz ikkilik sanoq sistemasida 12 ni 1100 ekanligini
bilamiz , biz pozitsiyani ko'ramiz eng kam ahamiyatga ega to'plam o'ng tomonda
bit, x-bu 3.
Bu bit [12] ushbu oraliqning yig'indisini o'z ichiga oladi (13-23-1+1) ->
12i.e.9 -> 12.
29](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_29.png)
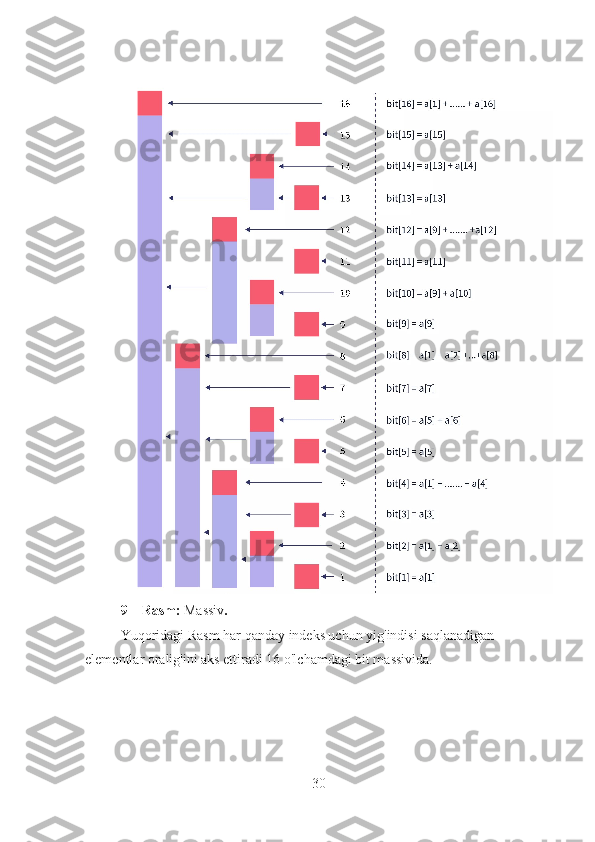
![Masalan: bitdagi 12-indeks diapazon [9 dan12 gacha] yig'indisini qiymatlari
ushlab turadi. bitdagi 8-indeks diapazon [1dan 8 gacha] . Shunday qilib,
prefiks_sum topish uchun[12] biz shunchaki topishingiz mumkin
bit[12] + bit[8] summani birma-bir hisoblash o'rniga.
10 – Rasm: Fenvik jadvali .
Misol: Biza A =[ a 0 , a 1 ,..., a n − 1 ] massiv berilgan bo’lsin. Bu Fenvik
daraxtini n ta elementdan iborat T massiv deb nomlaymiz.
T
i =
∑
k = F( i)i
a
k (4)
i = 0 … n-1 va F(i) - massiv ustida ishlash vaqtini tanlashga bog'liq bo'lgan
ba'zi funktsiyalar. U oddiy formula bilan berilgan:
F ( i )= i & (i+1) . (5)
& - bu mantiqiy AND. AND bilan raqamlar va uning qiymatlari bittaga
ko'paytirilsa, biz bu raqamni ketma-ket so'nggi birliklarsiz olamiz.
Bu funksiyani boshqa formula orqali topsaham bo’ladi .
31](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_31.png)

![nolga teng bo'ladi. Ularni yana birliklarga aylantirish uchun biz OR operatsiyasini
qo'llaymiz
Shunday qilib, oxiridagi barcha nollar birliklarga aylanadi va biz kerakli
elementni olamiz. Ushbu ketma-ketlikning to'g'riligini tushunish uchun jadvalga
qarash kifoya.
12 – Rasm: Fenvik jadvali .
Shuni ta'kidlash kerakki, bu ketma-ketlik qat'iy ravishda o'sib boradi va eng
yomon holatda logaritma marta qo'llaniladi, chunki u har safar i sonining ikkilik
kengayishida bitta birlikni qo'shadi. a(i) elementiga qo'shiladigan funktsiyani
yozamiz d raqami va bu jarayonda tegishli qisman summalarni o'zgartiradi. Chunki
bizning qatorimiz N ni o'z ichiga oladi elementlar, keyin biz i(next)ni qidiramiz N
qiymatidan oshmaguncha.
function modify(i, d):
while i < N
t[i] += d
i = i | (i + 1)
Ko'pincha siz a(i) bilan x elementining qiymatini almashtirishingiz kerak bo'lgan
vazifani topishingiz mumkin.
function set(i, x):
d = x - a[i]
a[i] = x
modify(i, d)
33](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_33.png)
![Daraxtni qurish uning tavsifi asosida amalga oshirilishi mumkin. Ammo modify
funksiyasidan foydalansangiz tezroq bo'ladi a qatorining har bir elementi uchun
Keyin biz o(nlogn)ish vaqtini olamiz.
function build():
for i = 0 to N - 1
modify(i, a[i])
Amalga oshirish
Sum(i)funktsiyasining kodini beramiz :
int sum(i):
result = 0
while i >= 0
result += t[i]
i = f(i) - 1
return result
4.2. Fenvik daraxti va segment daraxtini taqqoslash. Fenvik daraxti
segmentlar daraxtiga qaraganda bir marta kamroq xotirani doimiy ravishda
egallaydi. Buning sababi shundaki, Fenvik daraxti faqat ba'zi elementlar uchun
operatsiya qiymatini saqlaydi va segmentlar daraxti elementlarning o'zini va
operatsiyaning qisman natijalarini pastki kesmalarda saqlaydi, shuning uchun u
kamida ikki baravar ko'p xotirani oladi.
Fenvik daraxtini amalga oshirish osonroq.
Fenvik daraxti qurilayotgan segmentdagi operatsiya qaytarilishi kerak, ya'ni
segmentdagi minimal (maksimal kabi) bu daraxtni segment daraxtidan farqli
o'laroq hisoblash mumkin emas. Ammo agar biz prefiksda minimal miqdorni
topishimiz kerak bo'lsa, unda Fenvik daraxti bu vazifani bajaradi. Bunday Fenvik
daraxti massiv elementlarini kamaytirish operatsiyasini qo'llab-quvvatlaydi.
Daraxtdagi minimalni qayta hisoblash prefiksdagi minimum massivini
yangilashdan ko'ra tezroq.
34](/data/documents/893a7915-9aa1-45d2-9261-49d4fd9bd093/page_34.png)


“ Fenvik daraxti MUNDARIJA: KIRISH …………………………………………………………………………… 3 1. Fenvik daraxti va uning ishlash prinsipi ……………………………………4 1.1. Operatsiya F …………………………………………………………………..5 1.2. Miqdorni hisoblash …………………………………………………………...6 1.3. Daraxt segmentlari bilan taqqoslash ..……………………………………… 7 2. Dasturlash tillarida amalga oshirish………… … …………………… ………12 2.1. C dasturlash tilida amalga oshirish………… … …………………… ……… 12 2.2. C ++ dasturlash tilida amalga oshirish ………… … ………………….. …… 15 2.3. Python dasturlash tilida amalga oshirish ……… … ………………….. …… 16 2.4. Java dasturlash tilida amalga oshirish ……… … ………………….. ……… 17 3. Fenvik daraxtiga vizual kirish … ………………………………… …………. 19 3.1. Fenvik Daraxti … …………………………………………..…… …………. 22 4. Fenvik daraxti / ikkilik indekslangan daraxtlar ……………………………28 4.1. Fenvik daraxtining asosiy g'oyasi. ………………………………………… 29 4.2. Fenvik daraxti va segment daraxtini taqqoslash …………………………34 XULOSA ... ……………………………………………………………………… 35 FOYDAL ANILGAN ADABIYOTLAR ..……………………………………… 36 1
EJ KIRISH Fenvik daraxti yoki ikkilik indekslangan daraxt (ingl. binary indexed tree) - ko'p vazifalarda segmentlar daraxtini almashtiradigan, lekin ayni paytda uch yoki to’rt baravar tezroq ishlaydigan, mumkin bo'lgan minimal xotira miqdorini (bir xil uzunlikdagi massiv bilan bir xil) egallaydigan ma'lumotlar tuzilishi tezroq yoziladi va katta o'lchamlarga osonroq umumlashtiriladi. Fenvik daraxti-amalga oshirish oson, tez ishlaydi, lekin nazariy jihatdan mutlaqo aniq bo'lmagan ma'lumotlar tuzilishi, bu sizga prefiksdagi summani topishga va o(logN) uchun alohida elementlarni o'zgartirishga imkon beradi. Xuddi shu murakkablikka qaramay, Fenvik daraxti segmentlar daraxtiga qaraganda ancha tezroq ishlaydi. Ushbu ma'ruzada Fenvik daraxtining aniq ishlash printsipi berilmaydi, faqat amalga oshirish va foydalanish usullari ko'rsatiladi. Fenvik daraxti segmentlar daraxtiga qaraganda bir marta kamroq xotirani doimiy ravishda egallaydi. Buning sababi shundaki, Fenvik daraxti faqat ba'zi elementlar uchun operatsiya qiymatini saqlaydi va segmentlar daraxti elementlarning o'zini va operatsiyaning qisman natijalarini pastki kesmalarda saqlaydi, shuning uchun u kamida ikki baravar ko'p xotirani oladi. Fenvik daraxtini amalga oshirish osonroq. Fenvik daraxti qurilayotgan segmentdagi operatsiya qaytarilishi kerak, ya'ni segmentdagi minimal (maksimal kabi) bu daraxtni segment daraxtidan farqli o'laroq hisoblash mumkin emas. Ammo agar biz prefiksda minimal miqdorni topishimiz kerak bo'lsa, unda Fenvik daraxti bu vazifani bajaradi. Bunday Fenvik daraxti massiv elementlarini kamaytirish 2
operatsiyasini qo'llab-quvvatlaydi. Daraxtdagi minimalni qayta hisoblash prefiksdagi minimum massivini yangilashdan ko'ra tezroq. 1.Fenvik daraxti va uning ishlash prinsipi Fenvik daraxti-bu ma'lumotlar tuzilishi, massivdagi daraxt, quyidagi xususiyatlarga ega: 1) O (log N) vaqtidagi har qanday [L; R] segmentidagi ba'zi qaytariladigan g operatsiyasining qiymatini hisoblash imkonini beradi; 2)har qanday elementning qiymatini O (log N) ga o'zgartirishga imkon beradi; 3) O (N) xotirani talab qiladi, aniqrog'i N elementlar qatori bilan bir xil; 4) Ko'p o'lchovli massivlar uchun osongina umumlashtiriladi. Fenvik daraxtining eng keng tarqalgan ishlatilishi segmentdagi yig'indini hisoblashdir, ya'ni funktsiya G (X1,..., Xk) = X1 + ... + Xk. Fenvik daraxti birinchi marta "a new data structure for cumulative frequency tables" (Peter M. Fenwick, 1994) maqolasi bilan tasvirlangan. Sum funktsiyasi a qatorining barcha elementlari bo'ylab harakatlanadigan joyga t qatori bo'ylab harakatlanib, iloji boricha segmentlar bo'ylab "sakrash" ni amalga oshiradi. Birinchidan, u [F(R); R] segmentidagi summaning qiymatini javobga qo'shadi, so'ngra [F(F(R)-1); F(R)-1] segmentidagi summani oladi va hokazo nolga yetguncha. Upd funktsiyasi teskari yo'nalishda - indekslarni ko'paytirish tomon siljiydi, TJ yig'indisi qiymatlarini faqat kerakli pozitsiyalar uchun yangilaydi, ya'ni f(j) <= i <= j bo'lgan barcha j uchun. shubhasiz, ikkala operatsiyaning tezligi F funktsiyasini tanlashga bog'liq bo'ladi. F(X) qiymatini quyidagicha aniqlaymiz: 3
F(X) = X & (X+1) (1) F(j) ni topish < = i < = j formulaga mos keladi: H(X) = X / (X+1) (2) 1.1. Operatsiya F. F operatsiyasini turli yo'llar bilan tanlash mumkin, lekin ko'pincha interval yig'indisi operatsiyalari, interval mahsuloti, shuningdek ma'lum bir modifikatsiya va cheklovlar, intervalda maksimal va minimalni topish yoki boshqa operatsiyalar olinadi. Eng oddiy vazifa Massivning ketma-ket elementlari yig'indisini topish muammosini ko'rib chiqing. Ko'p so'rovlar bo'lishini hisobga olsak, s (L, R) ni topishingiz kerak bo'lgan shakl (L,R)- a[L] dan a[R] gacha bo'lgan barcha elementlarning yig'indisi. Ushbu muammoning eng oddiy echimi qisman summalarni topish bo'ladi. Ularni topgandan so'ng, biz ushbu summalarni sum[i]=a[1]+a[2]...+a[i]. bo'lgan qatorga yozamiz...+ a[i]. Keyin so'rovda talab qilinadigan qiymat S(L,R)=sum[R]-sum[L-1] (sum[0] odatda alohida holatlarni hisobga olmaslik uchun nolga teng deb hisoblanadi). Kamchiliklari - ushbu vazifani amalga oshirishda muhim kamchiliklar mavjud. Va asosiylaridan biri shundaki, asl massivning bitta elementini o'zgartirganda, o'rtacha O(N) qisman summalarni qayta hisoblash kerak va bu vaqt talab etadi. Ushbu muammoni hal qilish uchun siz Fenvik daraxtidan foydalanishingiz mumkin. Afzalliklari - Ushbu dizaynning asosiy afzalligi-amalga oshirish qulayligi va so'rovlarga javoblarning tezligi O (1). Fenvik daraxtining ushbu vazifa uchun qo'llanilishi. Tabiiy sonlarda aniqlangan va x&(x+1) (&- bit va) ga teng bo'lgan g (x) funktsiyasini kiritamiz. Shunday qilib, g (x) x ga teng, agar x ning ikkilik kengayishida oxirgi 0 bo'lsa (x 2 ga bo'linadi). Va agar ikkilik kengayishda x kichik raqamlarda birliklar guruhi mavjud bo'lsa, unda funktsiya x ga teng bo'lib, oxirgi birliklar 0 ga almashtiriladi. Bu x & (x+1) ekanligiga misollar bilan ishonch hosil qilishingiz mumkin. 4
Endi biz quyidagi qisman summalarni hisoblaymiz va ularni t[i] = a[G[i]] + a[G[i]+1]…+ a[i] ga yozamiz. Keyinchalik, ushbu summalarni qanday topish mumkinligi ko'rsatiladi. 1.2. Miqdorni hisoblash. S(L,R) ni topish uchun s(1, L-1) va s(1,R) ni qidiramiz. Agar t qatori bo'lsa, s(L, R) ni topadigan funktsiyani yozamiz. Bunday holda, chap uchi summaga kiritilmaydi, lekin uni yoqish oson agar bu vazifada talab qilinsa (kodga qarang). const int N = 100; int t[N],a[N]; int sum(int L, int R) { int res=0; while (R >= 0) { res += t[R]; R = G( R ) - 1; } while (L >= 0) { res -= t[L]; L = G(L) - 1; } return res; } Shuni ham ta'kidlash kerakki, har bir dastur uchun g funktsiyasi x ikkilik yozuvidagi birliklar sonini kamida 1 ga kamaytiradi. Shundan kelib chiqadiki, summani hisoblash O (log N) uchun amalga oshiriladi. Elementlarni o'zgartirish. Endi elementlarning modifikatsiyasini ko'rib chiqing. Elementlarning qanday o'zgarishiga qarab qisman summalarni tezda 5
