Eng katta qismiy ketma-ketlikni qidirish



![Ketma-ket qidiruv algoritmi C++ tilida quyidagicha bo’ladi:
int qidiruv(int key)
{ for (int i=0;i<n;i++)< p=""></n;i++)<>
if (k[i]==key) { search = i;return search;}
search = -1;
return search;
}
}
Massivda ketma-ket qidiruv algoritmi samaradorligini bajarilgan
taqqoslashlar soni M bilan aniqlash mumkin. M
min = 1, M
max = n. Agar
ma’lumotlar massiv yacheykasida bir xil ehtimollik bilan taqsimlangan
bo’lsa, u holda M
o’rt (n + 1)/2 bo’ladi. Agar kerakli element jadvalda
yo’q bo’lib, uni jadvalga qo’shish lozim bo’lsa, u holda yuqorida keltirilgan
algoritmdagi oxirgi ikkita operator quyidagicha almashtiriladi .
n=n+1;
k[n-1]:=key;
r[n-1]:=rec; search:=n-1;
return search;
Agar ma’lumotlar jadvali bir bog’lamli ro’yhat ko’rinishida berilgan
bo’lsa , u holda ketma-ket qidiruv ro’yhatda amalga oshiriladi.
1-Rasm
Chiziqli bir bog’lamli ro’yhatdan key kalitga mos elementni ketma-ket
qidiruv usuli yordamida izlab topish dasturi.
Node *q=NULL;
Node *p=lst;
while (p !=NULL){
4](/data/documents/928bb12e-355b-4b6c-aa37-c43dd5e7b75d/page_4.png)

![M ixtiyoriy tanlanganda ham taklif qilinayotgan algoritm korrekt
ishlaydi. Shu sababali M ni shunday tanlash lozimki, tadqiq qilinayotgan
algoritm samaraliroq natija bersin, ya’ni uni shunday tanlaylikki, iloji boricha
kelgusi jarayonlarda ishtirok etuvchi elementlar soni kam bo’lsin. Agar biz
o’rtacha elementni, ya’ni massiv o’rtasini tanlasak yechim mukammal
bo’ladi. Misol uchun butun sonlardan iborat, o’sish bo’yicha tartiblangan
massivdan ikkilik qidiruv usuli yordamida key kalitga mos elementni izlash
dasturini ko’rib chiqamiz.
1.3 Dastur kodi:
#include <iostream>
using namespace std ;
int main(){
int n;cout<<"n=";cin>>n;
int k[n];
for(int i=0;i>k[i];
int key, search;
cout<<"qidirilayotgan elementni kiriting=";cin>>key;
int low = 0;
while (low <= hi){
int mid = (low + hi) / 2;j++;
if (key == k[mid]){
search = mid;
cout<<"qidirilayotgan element "<<search+1<<" o’rinda="" turibdi=""
va="" u="" "<<j<<"="" ta="" solishtirishda="" toplidi\n";<=""
p=""></search+1<<">
system("pause");
exit(0);
}
if (key < k[mid])
hi = mid - 1;
6](/data/documents/928bb12e-355b-4b6c-aa37-c43dd5e7b75d/page_6.png)





![II. Qismiy ketma-ketlikni qidirish uchun Knut Morris Pratt
algoritmi
2.1 Knut Morris Pratt algoritmi haqida
Knut-Morris-Pratt algoritmi. Matnda namuna satrni izlovchi ch е kli
avtomat qurishda boshlang`ich holatdan tugallovchi holatga o’tishlar namuna
satrga kiruvchi simvollar bilan b е lgilab olinadi. Asosiy muammo namuna
satrga tugallovchi holatga olib k е lmaydigan simvollarni qo’shish jarayonida
vujudga k е ladi.
Knut-Morris-Pratt algoritmi ch е kli avtomat printsipiga asoslanadi, ammo
unda mos tushmaydigan simvollarni qayta ishlashning boshqaa usulidan
foydalaniladi. Ushbu algoritmda ch е kli avtomat holatlari ayni paytda mos
tushishi k е rak bo’lgan simvollar orqali b е lgilab olinadi. Har bir holatda ikki
yo’nalishda o’tish imkoniyati mavjud: birinchisi – mos tushish ro’y b е rgan
holat; ikkinchisi – mos tushish ro’y b е rmagan holatga to’g’ri k е ladi. Mos
tushish ro’y b е rganda avtomatning k е yingi tugunga o’tishi yuzb е radi, aks
holda joriy tugundan oldingi (orqaga) tugunga o’tish yuz b е radi. Quyidagi
tasvirda ababcb namuna satri uchun tuzilgan Knut-Morris-Pratt avtomatining
sx е matik tuzilishi ifoda etilgan:
Har bir muvaffaqiyatli o’tish bajarilganda Knut-Morris-Pratt ch е kli
avtomatida matndan yangi simvol tanlanadi. Muvaffaqiyatsiz o’tishlarda yangi
simvol tanlanmasdan, buning o’rniga oxirgi marta tanlangan simvol takroran
qayta ishlanadi. Agar avtomat tugallovchi holatga o’tsa, matndan namuna
satr topildi d е b, hisoblanadi. Quyida ushbu algoritm matnini k е ltiramiz:
subLoc=1// Namuna satrdagi taqqoslanuvchi joriy simvol ko’rsatkichi
textLoc=1//Matndagi taqqoslanuvchi joriy simvol ko’rsatkichi
while textLoc<=length(text) and subLoc<=length(substring) do
if subLoc=0 or text [textLoc]=substring[subLoc] then
textLoc=textLoc+1
subLoc= subLoc+1
else // mos tushmaslik yuz b е rdi; mos tushmaslik bo’yicha o’tish
subLoc=fail[subLoc]
12](/data/documents/928bb12e-355b-4b6c-aa37-c43dd5e7b75d/page_12.png)

![Knuth-MorrisPratt (KMP) algoritmi mana shu muammoga yechim
sifatida kelib, qidiruvni boshqatdan boshlamaslikning imkonini beradi. U
Deterministic Finite Automaton g’oyasiga asoslangan.
2.2 Patterndan DFA yasash:
Yuqoridagi jadval va graph’ni biz o’zimi ko’rib turib yasadik. Kodda
qanday qilib berilgan pattern’dan DFAni yasaymiz?
DFAni yasashda ikki xil holat bor:
Mos kelish . j-holatida, keyingi belgi c == pattern.charAt(j) bo’lsa, u
holda j ni bittaga oshiramiz.
Mos kelmaslik . j-holatida, keyingi belgi c != pattern.charAt(j) bo’lsa,
u holda ohirgi j-1 belgilar pattern[1..j-1] ichida bo’ladi.
1-Jadval:
function dfaGenerator ( pattern ) {
R = 128
const M = pattern . length
const dfa = [ ... Array ( R ). fill ( null )]. map (() => Array ( M ). fill ( 0 ))
dfa [ pattern . charCodeAt ( 0 )][ 0 ] = 1
for ( let x = 0 , j = 1 ; j < M ; j ++ ) {
for ( let c = 0 ; c < R ; c ++ ) {
// Copy mismatched cases
dfa [ c ][ j ] = dfa [ c ][ x ]
// Set match case
dfa [ pattern . charCodeAt ( j )][ j ] = j + 1
14](/data/documents/928bb12e-355b-4b6c-aa37-c43dd5e7b75d/page_14.png)
![// Update restart state
x = dfa [ pattern . charCodeAt ( j )][ x ]
}
}
return dfa
}
2.3 Knuth-Morris-Pratt algoritmini kodda ifodalash
function KMPSearch ( str , pattern ) {
const N = str . length
const M = pattern . length
const dfa = dfaGenerator ( pattern )
let i , j
if ( ! N || ! M ) {
return -1
}
for ( i = 0 , j = 0 ; i < N && j < M ; i ++ ) {
j = dfa [ str . charCodeAt ( i )][ j ]
}
if ( j === M ) {
return i – M
}
15](/data/documents/928bb12e-355b-4b6c-aa37-c43dd5e7b75d/page_15.png)
![else {
return N
}
function dfaGenerator ( pattern ) {
R = 128
const M = pattern . length
const dfa = [ ... Array ( R ). fill ( null )]. map (() => Array ( M ). fill ( 0 ))
dfa [ pattern . charCodeAt ( 0 )][ 0 ] = 1
for ( let x = 0 , j = 1 ; j < M ; j ++ ) {
for ( let c = 0 ; c < R ; c ++ ) {
// Copy mismatched cases
dfa [ c ][ j ] = dfa [ c ][ x ]
// Set match case
dfa [ pattern . charCodeAt ( j )][ j ] = j + 1
// Update restart state
x = dfa [ pattern . charCodeAt ( j )][ x ]
}
}
return dfa
}
}
16](/data/documents/928bb12e-355b-4b6c-aa37-c43dd5e7b75d/page_16.png)


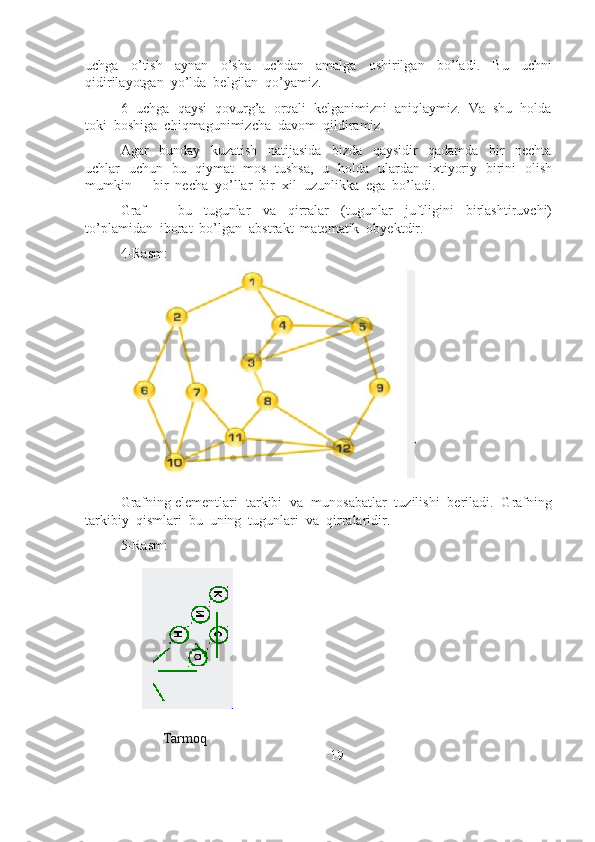

![ma'lumotlarni saqlash uchun va topilgan eng qisqa yo'llar kiritiladigan butun
toifadagi - distance . G={V,E} graf berilgan bo’lsin. V to’plamga tegishli
barcha tugunlar dastlab tashrif buyurilmagan deb belgilanadi, ya’ni visited
massivining elementlariga false qiymat berib chiqiladi. Eng afzal yo’lni
topish masalasi qaralyapti. Distance massivining har bir elementiga shunday
qilib beriladiki, ixtiyoriy potensial yo’ldan katta bo’lsin (odatda, bu qiymatni
cheksiz katta qiymat deb qaraladi, ammo dasturda berilgan toifaning
qiymatlar diapazonidagi eng katta qiymat sifatida olinadi). Boshlang'ich nuqta
sifatida s tugun tanlanadi va unga nol yo'l belgilanadi: distance [s] = 0,
chunki s-dan s-gacha hech qanday qirra yo'q (bu usulda ilmoqlar
qaralmaydi).
Shundan keyin, barcha qo'shni tugunlar topiladi (s dan chiquvchi
qirralar orqali) [ularni t va u deb belgilaylik] va ular birma-bir tekshirib
ko'riladi, ya'ni s tugundan har bir tugungacha birma-bir marshrut bahosi
hisoblanadi:
- distance[t]=distance[s]+ s va t orasidagi qirraning vazni;
- Distance[u]=distance[s]+ s va u orasidagi qirraning vazni.
Ehtimoldan xoli emaski, u yoki bu tugunga s dan bir qancha yo’llar
bo’lishi mumkin. Shu sababli, distance massivida bu tugunga bo’lgan
yo’lning vaznini qayta ko’rib chiqish kerak bo’ladi. Shunda kattaroq
(nooptimal) qiymat yo’qotiladi va tugunga mos yo’lning vazniga kichikroq
qiymat beriladi. s tugun bilan qo’shni bo’lgan va qarab chiqilgan tugunlar
tashrif buyurilgan sifatida belgilab chiqiladi, yani visited[s]=true va natijada,
s dan chiquvchi, minimal vaznga ega bo’lgan yo’l eltuvchi tugun faol
element sifatida belgilab olinadi. Faraz qilamiz, s dan u gacha masofa t ga
qaraganda qisqa bo’lsin. Kelib chiqadiki, u tugun faollashadi va yuqoridagi
kabi uning qo’shnilari ( s dan tashqari) o’rganilib chiqiladi. u tugun tashrif
buyurilgan deb belgilanadi: visited[u]=true, endi t tugun faollashadi va
yuqoridagi prosedura uning uchun takrorlanadi. Deykstra algoritmi s
tugundan borish mumkin bo’lgan barcha tugunlar tadqiq qilinmaguncha davom
ettiriladi.
Algoritm tarixi uchta mustaqil matematiklar bilan bog'liq: Lester Ford,
Richard Bellman va Edward Moore. Ford va Bellman algoritmni 1956 va
1958 yillarda nashr etishdi, Moore esa 1957 yilda taqdim qilgan. Va ba'zan
uni Bellman-Ford-Moore algoritmi deb ham atashadi. Usul ba'zi vektorli-
marshrutlash protokollarida, masalan, RIPda (Routing Information Protocol)
qo'llaniladi. Deykstra algoritmi singari, Bellman-Ford algoritmi ham vaznga
21](/data/documents/928bb12e-355b-4b6c-aa37-c43dd5e7b75d/page_21.png)



“Eng katta qismiy ketma-ketlikni qidirish” MUNDARIJA KIRISH. .......................................................................................................... 2 I Qismiy ketma-ketlikni qidirish ..................................................................... 3 1.1 Ketma-ket qidiruv algoritmi .................................................................. 3 1.2 Teng bo’lish orqali qidiruv (ikkilik qidiruv) algoritmi ......................... 5 1.3 Dastur kodi: ........................................................................................... 6 1.4 Indeksli ketma-ket qidiruv algoritmi. .................................................... 9 II. Qismiy ketma-ketlikni qidirish uchun Knut Morris Pratt algoritmi ......... 12 2.1 Knut Morris Pratt algoritmi haqida ..................................................... 12 2.2 Patterndan DFA yasash: ...................................................................... 14 2.3 Knuth-Morris-Pratt algoritmini kodda ifodalash ................................. 15 III. Deykstra algoritmi .................................................................................. 20 XULOSA ....................................................................................................... 22 FOYDALANILGAN ADABIYOTLAR ....................................................... 24
KIRISH. Algoritm tushunchasi zamonaviy matematika va informatikaning asosiy tushunchalaridan biri hisobanadi. Algoritm ma’lum bir turga oid masalalarni yechishda ishlatiladigan amallarning muayyan tartibda bajarilishi haqidagi qoida hisoblanadi. “Qismiy ketma-ketlikni qidirish” asosan, algoritmda bu mavzuni yoritishimizda qidiruv nima ekanligiga to’xtalib o’tsak. Ma’lumotlarni qidirish algoritmlari bu- to’plam ma’lumotlar orasidan ma’lum bir kalit so’zga mos keluvchi elimentlarni qidirishga aytiladi. Ma’lumotlarni qidirish algoritmlari odatda ikki toifaga bo’linadi va bular quydagilar: Tarkibiy qidiruv: Bunda ro’yxat yoki qator ketma- ket o’tkaziladi va har bir eliment tekshiriladi. Bunga misol sifatida chiziqli qidiruvni keltirsak bo’ladi. Qidirish algoritmining eng soddasi bo’lgan chiziqli qidirish algoritmi, chiziqli ma’lumotlar tuzulmalaridan biror bir shart yoki qiymat bo’yicha eliment qidirishga mo’ljallangan va uning algoritmik murakkabligi quydagicha: Chiziqli qidirish algoritmining vaqt bo’yicha murakkabligi uning nomidan ham ma’lum, ya’ni chiziqli O(n). Ya’ni, eng yomon holat sifatida eliment array bo’lmagan holat qaraladi va bunda algoritm maximum n ta qadam ish bajarishi kerak bo’ladi. Intervalli qidirish- bu algoritmar maxsus ajratilgan ma’lumotlar tuzilmalarida qidirish uchun mo’ljallangan. Ushbu turdagi qidiruv algoritmlari Linear Search-ga qaraganda ancha samaralidir, chunki ular qayta-qayta qidiruv tuzulmasi markaziga yo’naladi va qidiruv maydonini ikkiga bo’ladi. Masalan: Ikkilik qidiruv. Ikkilik qidiruv- bu algoritmi asosan to’plamni ikkiga bo’lishlar orqali qidirishdan iborat. Ya’ni unda bo’linishlar toki kalit so’z topulmaganicha davom etadi. 2
I Qismiy ketma-ketlikni qidirish Kompyuterda ma’lumotlarni qayta ishlashda qidiruv asosiy amallardan biri hisoblanadi. Uning vazifasi berilgan argument bo’yicha massiv ma’lumotlari ichidan mazkur argumentga mos ma’lumotlarni topish yoki bunday ma’lumot yo’qligini aniqlashdan iborat. Ixtiyoriy ma’lumotlar majmuasi jadval yoki fayl deb ataladi. Ixtiyoriy ma’lumot (yoki tuzilma elementi) boshqa ma’lumotdan biror bir belgisi orqali farq qiladi. Mazkur belgi kalit deb ataladi. Kalit noyob bo’lishi, ya’ni mazkur kalitga ega ma’lumot jadvalda yagona bo’lishi mumkin. Bunday noyob kalitga boshlang’ich (birinchi) kalit deyiladi. Ikkinchi kalit bir jadvalda takrorlansada u orqali ham qidiruvni amalga oshirish mumkin. Ma’lumotlar kalitini bir joyga yig’ish (boshqa jadvalga) yoki yozuv sifatida ifodalab bitta maydonga kalitlarni yozish mumkin. Agar kalitlar ma’lumotlar jadvalidan ajratib olinib alohida fayl sifatida saqlansa, u holda bunday kalitlar tashqi kalitlar deyiladi. Aks holda, ya’ni yozuvning bir maydoni sifatida jadvalda saqlansa ichki kalit deyiladi. Kalitni berilgan argument bilan mosligini aniqlovchi algoritmga berilgan argument bo’yicha qidiruv deb ataladi. Qidiruv algoritmi vazifasi kerakli ma’lumotni jadvaldan topish yoki yo’qligini aniqlashdan iboratdir. Agar kerakli ma’lumot yo’q bo’lsa, u holda ikkita ishni amalga oshirish mumkin: 1. Ma’lumot yo’qligini indikatsiya qilish (belgilash) 2. Jadvalga ma’lumotni qo’yish. Faraz qilaylik, k – kalitlar massivi. Har bir k(i) uchun r(i) – ma’lumot mavjud. Key – qidiruv argumenti. Unga rec - informatsion yozuv mos qo’yiladi. Jadvaldagi ma’lumotlarning tuzilmasiga qarab qidiruvning bir necha turlari mavjud. 1.1 Ketma-ket qidiruv algoritmi Mazkur ko’rinishdagi qidiruv agar ma’lumotlar tartibsiz yoki ular tuzilishi noaniq bo’lganda qo’llaniladi. Bunda ma’lumotlar butun jadval bo’yicha operativ xotirada kichik adresdan boshlab, to katta adresgacha ketma-ket qarab chiqiladi. Massivda ketma-ket qidiruv (search o’zgaruvchi topilgan element tartib raqamini saqlaydi). 3
Ketma-ket qidiruv algoritmi C++ tilida quyidagicha bo’ladi: int qidiruv(int key) { for (int i=0;i<n;i++)< p=""></n;i++)<> if (k[i]==key) { search = i;return search;} search = -1; return search; } } Massivda ketma-ket qidiruv algoritmi samaradorligini bajarilgan taqqoslashlar soni M bilan aniqlash mumkin. M min = 1, M max = n. Agar ma’lumotlar massiv yacheykasida bir xil ehtimollik bilan taqsimlangan bo’lsa, u holda M o’rt (n + 1)/2 bo’ladi. Agar kerakli element jadvalda yo’q bo’lib, uni jadvalga qo’shish lozim bo’lsa, u holda yuqorida keltirilgan algoritmdagi oxirgi ikkita operator quyidagicha almashtiriladi . n=n+1; k[n-1]:=key; r[n-1]:=rec; search:=n-1; return search; Agar ma’lumotlar jadvali bir bog’lamli ro’yhat ko’rinishida berilgan bo’lsa , u holda ketma-ket qidiruv ro’yhatda amalga oshiriladi. 1-Rasm Chiziqli bir bog’lamli ro’yhatdan key kalitga mos elementni ketma-ket qidiruv usuli yordamida izlab topish dasturi. Node *q=NULL; Node *p=lst; while (p !=NULL){ 4
if (p->k == key){ search = p; return search; } q = p; p = p->nxt; } Node *s=new Node;; s->k=key; s->r=rec; s->nxt= NULL; if (q == NULL){ s->nxt=lst; lst = s; } else q->nxt = s; search= s; return search; Ro’yhatli tuzilmaning afzalligi shundan iboratki, ro’yhatga elementni qo’shish yoki o’chirish tez amalga oshadi, bunda qo’shish yoki o’chirish element soniga bog’liq bo’lmaydi, massivda esa elementni qo’shish yoki o’chirish o’rta hisobda barcha elementlarning yarmini siljitishni talab qiladi. Ro’yhatda qidiruvning samaradorligi taxminan massivniki bilan bir xil bo’ladi. 1.2 Teng bo’lish orqali qidiruv (ikkilik qidiruv) algoritmi Faraz qilaylik, o’sish tartibida tartiblangan sonlar massivi berilgan bo’lsin. Ushbu usulning asosiy g’oyasi shundan iboratki, tasodifiy qandaydir A M element olinadi va u X qidiruv argumenti bilan taqqoslanadi. Agar A M =X bo’lsa, u holda qidiruv yakunlanadi; agar A M >X bo’lsa, u holda indekslari M dan katta bo’lgan barcha elementlar kelgusi qidiruvdan chiqarib yuboriladi. 5
