GRAFLAR ENG QISQA MASOFA TOPISH ALGORITMLAR


![Floyd Algoritmlari
Ushbu algoritm ba'zan Floyd-Warshell algoritmi deb ataladi. Floyd-Warshell
algoritmi 1962da Robert Floyd va Stiven Uorchell tomonidan ishlab chiqilgan
graflarda algoritmdir. Grafning barcha juftlari orasidagi eng qisqa yo'llarni topishga
xizmat qiladi. Floyd usuli to'g'ridan-to'g'ri qovurg'alarning ijobiy og'irliklari bo'lgan
ustunda, har qanday elementar bo'lmagan (1 qovurg'asidan ko'prog'ini o'z ichiga
olgan), eng qisqa yo'l boshqa eng qisqa yo'llardan iborat. Ushbu algoritm Dijkstra
algoritmiga nisbatan ancha keng tarqalgan, chunki har qanday ikki ustun o'rtasida
eng qisqa yo'llarnitopadi. Floyd algoritmida eng qisqa yo'llarning uzunligi
hisoblangan NxN matritsasi ishlatiladi. A[i,j] elementi, agar u erda chekka (i, j)
bo'lsa,yakuniy qiymatga ega bo'lgan va aks holda abadiylikka teng bo'lgan j ning
yuqori qismidan masofaga teng. Floyd Algoritmning asosiy g'oyasi. I, j, k ning uchta
tepasi bor va ular orasidagi masofa belgilanadi. Agar tengsizlik a[i,k]+a[k,j]<a[i,j]
bajarilsa, i->j yo'lini i->k->j bilan almashtirish tavsiya etiladi. Qadam 0. A0
masofasining dastlabki matritsasini va S0 vertexlarining ketma-ketligini aniqlang.
Har ikkala matritsaning har bir diagonali elementi 0ga teng, shuning uchun bu
elementlarning hisob-kitoblarda ishtirok etmasligini ko'rsatmoqda. K = 1 ga
ishonamiz. Asosiy qadam k. k satrini va k ustunini etakchi satr va etakchi ustun
sifatida belgilang. Yuqorida tavsiflangan AK-1 matritsasining barcha
elementlariga[i, j] almashtirishni ko'rib chiqamiz. Agar tengsizlik a[i,k]+a[k,j]<a[i,j],
(i\ne k, j\ne k, i\ ne j) bajarilsa, unda quyidagi harakatlar amalga oshiriladi:
A[i,k]+a[k,j] miqdori uchun A[i,j] elementining Ak-1 matritsasini almashtirish orqali
Ak matritsasini yarating] ; k g6a SK-1 element s[i,j] matritsasini almashtirish orqali
Sk matritsasini yarating. Shunday qilib, Floyd algoritmi n yinelemelerini qiladi, a
matritsasining i- yinelemesinden keyin, bu yo'llar birinchi dan i-chigacha bo'lgan
tepaliklardan o'tishi sharti bilan, har qanday ikki juftlik orasidagi eng qisqa
yo'llarning uzunligini o'z ichiga oladi. Har bir iteratsiya bo'ylab barcha juftlar ko'chib
o'tadi va ularning orasidagi yo'l i-tepa yordamida kamayadi.](/data/documents/149bece6-5bcf-473f-815b-e3d80597b66a/page_3.png)
![Misol 45.2. Floyd algoritmini namoyish qilish
// Floyd algoritm funktsiyasi tavsifi
void Floyd(int n, int **Graph, int **ShortestPath)
{ int i, j, k;
int Max_Sum = 0;
for ( i = 0 ; i < n ; i++ ) for ( j = 0 ; j < n ; j++ )
Max_Sum+= ShortestPath[i][j];
for ( i = 0 ; i < n ; i++)
if ( ShortestPath[i][j] == 0 && i!=j)
ShortestPath[i][j] = Max_Sum;
for ( k = 0 ; k <n;k++)
for ( i = 0 ; i < n; i++)
if ((ShortestPath[i][k] + ShortestPath[k][j])
ShortestPath[i][j] = ShortestPath[i][k] ;
Agar grafik yo'naltirilmagan bo'lsa, unda transformatsiyalar natijasida olingan
barcha matritsalar nosimmetrik bo'lib, shuning uchun faqat asosiy diagonaldan
yuqorida joylashgan elementlarni hisoblash kifoya.
Agar grafik qo'shni matritsasi bilan ifodalangan bo'lsa, unda bu algoritmning
ishlash vaqti o(n3) buyrug'iga ega, chunki u bir-biriga biriktirilgan uchta tsiklni o'z
ichiga oladi.](/data/documents/149bece6-5bcf-473f-815b-e3d80597b66a/page_4.png)
![Haddan tashqari algoritmlar
Bulkhead algoritmlari, odatda, optimal yechim topish uchun qidiruv
algoritmlari. Shu bilan birga, yechim asta-sekin ishlab chiqilgan. Bunday holda,
odatda, daraxt variantlarining ustunlarini qidirish haqida gap boradi. Bunday
ustunning tepalari oraliq yoki yakuniy variantlar bo'ladi va qovurg'alar variantlarni
loyihalash yo'llarini ko'rsatadi.Labirintdagi eng qisqa yo'lni topish vazifasi
misolida ustundagi qidiruv usullariga asoslangan juda ko'p algoritmlarni ko'rib
chiqing.
Muammo bayonoti.
O'tish va o'tkazilmaydigan hujayralardan tashkil topgan labirint mxn o'lchamli
a matritsasi bilan berilgan. Agar hujayra (i,j) o'tkazilsa, matritsaning elementi
a[i,j]=0. Aks holda, a [i,j]=\infty.Hujayradagi (1, 1) hujayradagi (m, n) eng qisqa
yo'lning uzunligini topish kerak.Aslida, qo'shni matritsa berilgan (faqat nollar
abadiylik bilan almashtiriladi va birliklar nolga teng). Labirint-bu grafik.Ushbu
vazifadagi variantlar daraxtining tepalari qafada boshlangan yo'llardir (1, 1).
Qovurg'alar-bu yo'llarning dizayni yo'lini ko'rsatadi va k va k+1 uzunliklarining
ikki yo'lini birlashtiradi, bu erda ikkinchi yo'l yana bir harakatning yo'lini birinchi
marta qo'shib olinadi.
Qaytish bilan qidirish. Ushbu usul chuqur qidirish uslubiga asoslangan. Qaytish
bilan qidirish sinov va xato usuli hisoblanadi ("keling, bu yo'nalishda borishga
harakat qilaylik – bu ishlamaydi - qaytib keling va boshqasiga harakat qilaylik").
Variantlarni qidirish chuqur qidirish usuli bilan amalga oshirilganligi sababli,
algoritm ish paytida daraxtdagi joriy yo'lni saqlash tavsiya etiladi. Bu yo'l bir yo'l
suyakka hisoblanadi.Bundan tashqari, bir qator Distga ehtiyoj bor, uning o'lchami
grafikaning vertikalari soniga mos keladi, bu har bir Vertex uchun dastlabki tepadan
masofani saqlaydi.](/data/documents/149bece6-5bcf-473f-815b-e3d80597b66a/page_5.png)





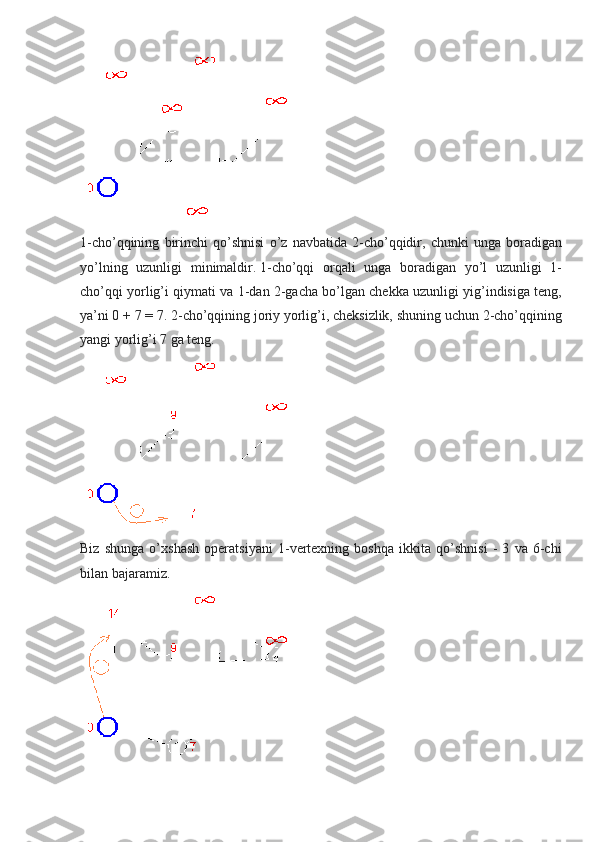


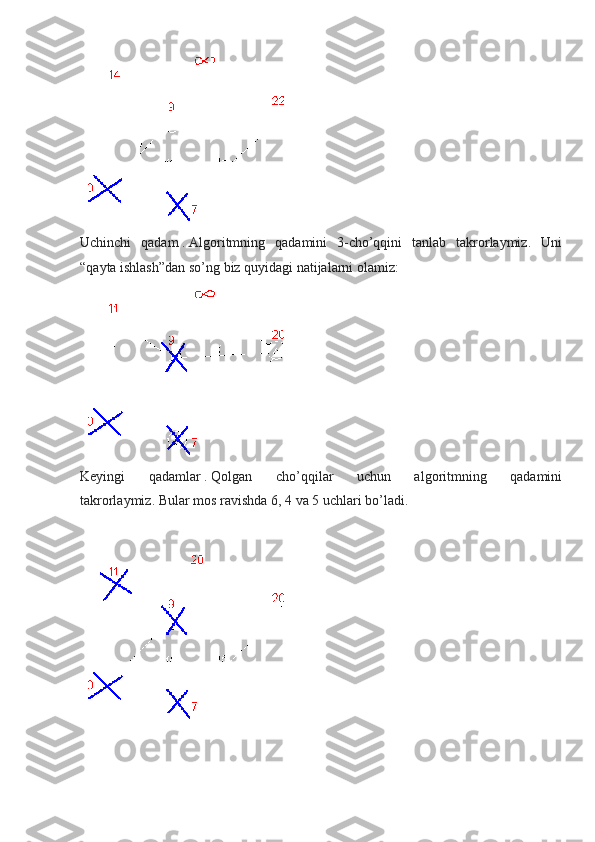

![shaharlarni ifodalasa va chekka xarajatlari to ’ g ’ ridan - to ’ g ’ ri yo ’ l bilan bog ’ langan
shaharlarning juftliklari o ’ rtasidagi masofani ifodalaydi ( oddiylik uchun , qizil
chiroqlar , ishlamaydigan belgilar , pullik yo ’ llar va boshqa to ’ siqlarni e ’ tiborsiz
qoldirish uchun ), Dijkstra algoritmi ishlatilishi mumkin Bir shahar va boshqa
shaharlarning eng qisqa yo ’ lini topish . Qisqa yo ’ l algoritmining keng tarqalgan
qo ’ llanilishi tarmoqni boshqarish protokollaridir , Shuningdek , Jonson kabi boshqa
algoritmlarda ham subroutin sifatida qo ’ llaniladi .
Dijkstra algoritmida musbat tamsay yoki haqiqiy sonlar bo’lgan etiketlar
ishlatiladi, bu aniq zaif tartibga solingan. Qiziqarli tomoni shundaki, Dijkstra aniq
belgilangan qisman tartibga ega bo’lgan va keyingi teglar (bir chekkadan o’tib
ketganda keyingi yorliq) monotonik ravishda kamaymaslik sharti bilan aniqlangan
teglardan foydalanish uchun umumlashtirilishi mumkin. Ushbu umumlashma
umumiy Dijkstra qisqa yo’l algoritmi deb ataladi.
Dijkstra algoritmini C++ dasturlash tilida ifodalanishi
#include<iostream>
#include<climits>
using namespace std;
int miniDist( int distance[], bool Tset[]) // minimal masofani topish
{
int minimum = INT_MAX,ind;
for ( int k = 0 ;k < 6 ;k ++ )
{
if (Tset[k] == false && distance[k] <= minimum)
{
minimum = distance[k];
ind = k;
}
}
return ind;](/data/documents/149bece6-5bcf-473f-815b-e3d80597b66a/page_16.png)
![}
void DijkstraAlgo( int graph[ 6 ][ 6 ], int src) // qo’shnilik matritsasi
{
int distance [ 6 ]; // har bir tugun uchun minimal masofani hisoblash uchun massiv
bool Tset[ 6 ]; // Har bir tugun uchun tashrif buyurilgan va tashrif buyurilmagan
belgilash uchun mantiqiy massiv
for ( int k = 0 ; k < 6 ; k ++ )
{
distance[k] = INT_MAX;
Tset[k] = false;
}
distance[src] = 0 ; // Manba tepasi masofasi 0 ga o’rnatiladi
for ( int k = 0 ; k < 6 ; k ++ )
{
int m = miniDist(distance,Tset);
Tset[m] = true;
for ( int k = 0 ; k < 6 ; k ++ )
{
// qo’shni vertex masofasini yangilash
If ( ! Tset [k] && graph[m][k] && distance[m] != INT_MAX && distance[m]
+ graph[m][k] < distance[k])
distance[k] = distance[m] + graph[m][k];
}
}
cout << " Vertex\t\tManba cho’qqisidan masofa " << endl;
for ( int k = 0 ; k < 6 ; k ++ )
{
char str = 65 + k;
cout << str << " \t\t\t " << distance[k] << endl;
}](/data/documents/149bece6-5bcf-473f-815b-e3d80597b66a/page_17.png)
![}
int main()
{
int graph[ 6 ][ 6 ] = {
{ 0 , 1 , 2 , 0 , 0 , 0 },
{ 1 , 0 , 0 , 5 , 1 , 0 },
{ 2 , 0 , 0 , 2 , 3 , 0 },
{ 0 , 5 , 2 , 0 , 2 , 2 },
{ 0 , 1 , 3 , 2 , 0 , 1 },
{ 0 , 0 , 0 , 2 , 1 , 0 }};
DijkstraAlgo(graph, 0 );
return 0 ;
}
Chiqish
Vertex Manbadan masofa
A 0 B 1 C 2 D 4 E 2 F 3
Vaqtning murakkabligi
Dijkstra algoritmining vaqt murakkabligi O(V^2) ga teng, bu erda V - grafdagi
cho’qqilar soni. Biroq, agar kirish grafigi qo’shnilik ro’yxati (grafni ko’rsatish usuli)
yordamida tasvirlangan bo’lsa, unda vaqt murakkabligini ikkilik to’p yordamida O(E
log V) ga kamaytirish mumkin.
Dijkstra algoritmining fazoviy murakkabligi O(V) ga teng, bu erda V - grafning
umumiy cho’qqilari soni. Buning sababi shundaki, biz ushbu barcha uchlarni
ro’yxatda chiqish sifatida saqlashimiz kerak.](/data/documents/149bece6-5bcf-473f-815b-e3d80597b66a/page_18.png)





“GRAFLAR ENG QISQA MASOFA TOPISH ALGORITMLAR” mavzusida Mundarija Floyd Algoritmlari ........................................................................................................................................ 3 Haddan tashqari algoritmlar ........................................................................................................................ 5 Qaytish bilan qidirish. Ushbu usul chuqur qidirish uslubiga asoslangan. Qaytish bilan qidirish sinov va xato usuli hisoblanadi ("keling, bu yo'nalishda borishga harakat qilaylik – bu ishlamaydi - qaytib keling va boshqasiga harakat qilaylik"). Variantlarni qidirish chuqur qidirish usuli bilan amalga oshirilganligi sababli, algoritm ish paytida daraxtdagi joriy yo'lni saqlash tavsiya etiladi. Bu yo'l bir yo'l suyakka hisoblanadi.Bundan tashqari, bir qator Distga ehtiyoj bor, uning o'lchami grafikaning vertikalari soniga mos keladi, bu har bir Vertex uchun dastlabki tepadan masofani saqlaydi. ............................................ 5 To'lqin algoritmi. Kenglik qidiruviga asoslangan bu ortiqcha algoritm ikki bosqichdan iborat: to'lqin tarqalishi; teskari harakat. To'lqinning tarqalishi va hujayralar tashrif buyuradigan usulning qadam raqami bilan belgilanadigan kenglikdagi qidiruv mavjud. Qaytish jarayonida, oxirgi tepadan boshlab, minimal belgilar bilan hujayralarni kiritish yo'li bilan unga kiritilgan yo'lni tiklash (misol 45.4). Muhim xususiyat shundaki, tiklanish oxiridan boshlanadi (boshidan bu ko'pincha mumkin emas). .................... 6 Graflar ustida amallar ............................................................................................................................ 19 Xulosa ........................................................................................................................................................ 22 Foydalanilgan adabiyotlar ......................................................................................................................... 23 Foydalanilgan Internet saytlar ................................................................................................................... 23
Kirish Qandaydir masalani xal etishga kirishishdan avval buning uchun eng yaxshi uslub izlanadi va uni qay tarzda tavsiflash aniqlanadi. Boshqacha qilib aytganda, biz doimo maqsadi ba’zi bir zaruriy natijaga erishishdan iborat, amallar ketma-ketligi bilan berilgan turli-tuman qoidalarga duch kelamiz. Bunday amallarning ketma- ketligi algoritm deb ataymiz. Matematikada algoritmning murakkabligi, xal etish masalalari va ularni ishlab chiqish prinsiplarini o’rganadigan maxsus “Algoritmlar nazariyasi” bo’limi xam mavjud. Algoritmlar nazariyasi – algoritmlarning umumiy xossalari, qonuniyatlari va ularni tasvirlanishining turli-tuman formal modellarini o’rganish bilan shug’ullanadi. Algoritm tushunchasini formallashtirish asosida ularning samaradorligi taqqoslash, ularning ekvivalentligi tekshirish, qo’llanilish sohasini aniqlash mumkin. Graflar nazariysida eng qisqa yo’lni aniqlash muhim klassik masalalaridan biri deb hisoblanadi. Uni hisoblash va echimlarni topish uchun bir qancha algoritmlari mavjud. Eng qisqa yo’l masalasi (inglizchada – shortest path problem) – bu grafning ikkita tugun orasidagi eng qichik yo’l (masofa, zanjir, marshrut) topish masalasidir, qaysidaki yoylarning vaznlarining yig’indisi minimal qiymatga ega. Qisqa (oddiy) zanjir geodezik zanjir ham aytiladi. Ushbu masalani adabiyotlarda bir nechta boshqa nomlanishi ham uchratish mumkin: minimal masofa masalasi, dilijans masalasi, qisqa masofa masalasi va boshqalar. Grafda eng qisqa masofani topish masalasi yo’naltirilgan, yo’naltirilmagan va aralash graflarda echimini aniqlash mumkin.
Floyd Algoritmlari Ushbu algoritm ba'zan Floyd-Warshell algoritmi deb ataladi. Floyd-Warshell algoritmi 1962da Robert Floyd va Stiven Uorchell tomonidan ishlab chiqilgan graflarda algoritmdir. Grafning barcha juftlari orasidagi eng qisqa yo'llarni topishga xizmat qiladi. Floyd usuli to'g'ridan-to'g'ri qovurg'alarning ijobiy og'irliklari bo'lgan ustunda, har qanday elementar bo'lmagan (1 qovurg'asidan ko'prog'ini o'z ichiga olgan), eng qisqa yo'l boshqa eng qisqa yo'llardan iborat. Ushbu algoritm Dijkstra algoritmiga nisbatan ancha keng tarqalgan, chunki har qanday ikki ustun o'rtasida eng qisqa yo'llarnitopadi. Floyd algoritmida eng qisqa yo'llarning uzunligi hisoblangan NxN matritsasi ishlatiladi. A[i,j] elementi, agar u erda chekka (i, j) bo'lsa,yakuniy qiymatga ega bo'lgan va aks holda abadiylikka teng bo'lgan j ning yuqori qismidan masofaga teng. Floyd Algoritmning asosiy g'oyasi. I, j, k ning uchta tepasi bor va ular orasidagi masofa belgilanadi. Agar tengsizlik a[i,k]+a[k,j]<a[i,j] bajarilsa, i->j yo'lini i->k->j bilan almashtirish tavsiya etiladi. Qadam 0. A0 masofasining dastlabki matritsasini va S0 vertexlarining ketma-ketligini aniqlang. Har ikkala matritsaning har bir diagonali elementi 0ga teng, shuning uchun bu elementlarning hisob-kitoblarda ishtirok etmasligini ko'rsatmoqda. K = 1 ga ishonamiz. Asosiy qadam k. k satrini va k ustunini etakchi satr va etakchi ustun sifatida belgilang. Yuqorida tavsiflangan AK-1 matritsasining barcha elementlariga[i, j] almashtirishni ko'rib chiqamiz. Agar tengsizlik a[i,k]+a[k,j]<a[i,j], (i\ne k, j\ne k, i\ ne j) bajarilsa, unda quyidagi harakatlar amalga oshiriladi: A[i,k]+a[k,j] miqdori uchun A[i,j] elementining Ak-1 matritsasini almashtirish orqali Ak matritsasini yarating] ; k g6a SK-1 element s[i,j] matritsasini almashtirish orqali Sk matritsasini yarating. Shunday qilib, Floyd algoritmi n yinelemelerini qiladi, a matritsasining i- yinelemesinden keyin, bu yo'llar birinchi dan i-chigacha bo'lgan tepaliklardan o'tishi sharti bilan, har qanday ikki juftlik orasidagi eng qisqa yo'llarning uzunligini o'z ichiga oladi. Har bir iteratsiya bo'ylab barcha juftlar ko'chib o'tadi va ularning orasidagi yo'l i-tepa yordamida kamayadi.
Misol 45.2. Floyd algoritmini namoyish qilish // Floyd algoritm funktsiyasi tavsifi void Floyd(int n, int **Graph, int **ShortestPath) { int i, j, k; int Max_Sum = 0; for ( i = 0 ; i < n ; i++ ) for ( j = 0 ; j < n ; j++ ) Max_Sum+= ShortestPath[i][j]; for ( i = 0 ; i < n ; i++) if ( ShortestPath[i][j] == 0 && i!=j) ShortestPath[i][j] = Max_Sum; for ( k = 0 ; k <n;k++) for ( i = 0 ; i < n; i++) if ((ShortestPath[i][k] + ShortestPath[k][j]) ShortestPath[i][j] = ShortestPath[i][k] ; Agar grafik yo'naltirilmagan bo'lsa, unda transformatsiyalar natijasida olingan barcha matritsalar nosimmetrik bo'lib, shuning uchun faqat asosiy diagonaldan yuqorida joylashgan elementlarni hisoblash kifoya. Agar grafik qo'shni matritsasi bilan ifodalangan bo'lsa, unda bu algoritmning ishlash vaqti o(n3) buyrug'iga ega, chunki u bir-biriga biriktirilgan uchta tsiklni o'z ichiga oladi.
Haddan tashqari algoritmlar Bulkhead algoritmlari, odatda, optimal yechim topish uchun qidiruv algoritmlari. Shu bilan birga, yechim asta-sekin ishlab chiqilgan. Bunday holda, odatda, daraxt variantlarining ustunlarini qidirish haqida gap boradi. Bunday ustunning tepalari oraliq yoki yakuniy variantlar bo'ladi va qovurg'alar variantlarni loyihalash yo'llarini ko'rsatadi.Labirintdagi eng qisqa yo'lni topish vazifasi misolida ustundagi qidiruv usullariga asoslangan juda ko'p algoritmlarni ko'rib chiqing. Muammo bayonoti. O'tish va o'tkazilmaydigan hujayralardan tashkil topgan labirint mxn o'lchamli a matritsasi bilan berilgan. Agar hujayra (i,j) o'tkazilsa, matritsaning elementi a[i,j]=0. Aks holda, a [i,j]=\infty.Hujayradagi (1, 1) hujayradagi (m, n) eng qisqa yo'lning uzunligini topish kerak.Aslida, qo'shni matritsa berilgan (faqat nollar abadiylik bilan almashtiriladi va birliklar nolga teng). Labirint-bu grafik.Ushbu vazifadagi variantlar daraxtining tepalari qafada boshlangan yo'llardir (1, 1). Qovurg'alar-bu yo'llarning dizayni yo'lini ko'rsatadi va k va k+1 uzunliklarining ikki yo'lini birlashtiradi, bu erda ikkinchi yo'l yana bir harakatning yo'lini birinchi marta qo'shib olinadi. Qaytish bilan qidirish. Ushbu usul chuqur qidirish uslubiga asoslangan. Qaytish bilan qidirish sinov va xato usuli hisoblanadi ("keling, bu yo'nalishda borishga harakat qilaylik – bu ishlamaydi - qaytib keling va boshqasiga harakat qilaylik"). Variantlarni qidirish chuqur qidirish usuli bilan amalga oshirilganligi sababli, algoritm ish paytida daraxtdagi joriy yo'lni saqlash tavsiya etiladi. Bu yo'l bir yo'l suyakka hisoblanadi.Bundan tashqari, bir qator Distga ehtiyoj bor, uning o'lchami grafikaning vertikalari soniga mos keladi, bu har bir Vertex uchun dastlabki tepadan masofani saqlaydi.
