Graflarda eng qisqa masofani topish algoritmlari








![Umuman, eng qisqa yo’llar masalalari kombinator optimallashtirishning
fundamental muammolaridandir. Ularning bir necha turlari mavjud, masalan,
ikkita berilgan uchlar orasida, berilgan va qolgan barcha uchlar orasida , turdagi
har bir uchlar juftliklari orasida va boshqalar.
2.3. Floyd Algoritmi
Ushbu algoritm ba'zan Floyd-Warshell algoritmi deb ataladi. Floyd-
Warshell algoritmi 1962da Robert Floyd va Stiven Uorchell tomonidan ishlab
chiqilgan graflar algoritmdir. Grafning barcha juftlari orasidagi eng qisqa
yo'llarni topishga xizmat qiladi. Floyd usuli to'g'ridan-to'g'ri qovurg'alarning
ijobiy og'irliklari bo'lgan ustunda, har qanday elementar bo'lmagan (1
qovurg'asidan ko'prog'ini o'z ichiga olgan), eng qisqa yo'l boshqa eng qisqa
yo'llardan iborat. Ushbu algoritm Dijkstra algoritmiga nisbatan ancha keng
tarqalgan, chunki u har qanday ikki ustun o'rtasida eng qisqa yo'llarni topadi.
Floyd algoritmida eng qisqa yo'llarning uzunligi hisoblangan NxN
matritsasi ishlatiladi. A[i,j] elementi, agar u erda chekka (i, j) bo'lsa,yakuniy
qiymatga ega bo'lgan va aks holda abadiylikka teng bo'lgan j ning yuqori
qismidan masofaga teng.
Floyd algoritm funktsiyasi tavsifi
void Floyd(int n, int **Graph, int **ShortestPath){
int i, j, k;
int Max_Sum = 0;
for ( i = 0 ; i < n ; i++ )
for ( j = 0 ; j < n ; j++ )
Max_Sum += ShortestPath[i][j];
for ( i = 0 ; i < n ; i++ )
9](/data/documents/8fcceb4f-45fc-41d8-879b-10efb35a3028/page_9.png)
![for ( j = 0 ; j < n ; j++ )
if ( ShortestPath[i][j] == 0 && i != j )
ShortestPath[i][j] = Max_Sum;
for ( k = 0 ; k < n; k++ )
for ( i = 0 ; i < n; i++ )
for ( j = 0 ; j < n ; j++ )
if ((ShortestPath[i][k] + ShortestPath[k][j]) <
ShortestPath[i][j])
ShortestPath[i][j] = ShortestPath[i][k] +
ShortestPath[k][j];
}
Agar graf yo'naltirilmagan bo'lsa, unda transformatsiyalar natijasida olingan
barcha matritsalar nosimmetrik bo'lib, shuning uchun faqat asosiy diagonaldan
yuqorida joylashgan elementlarni hisoblash kifoya.
Agar graf qo'shni matritsasi bilan ifodalangan bo'lsa, unda bu algoritmning
ishlash vaqti o(n3) buyrug'iga ega, chunki u bir-biriga biriktirilgan uchta tsiklni
o'z ichiga oladi.
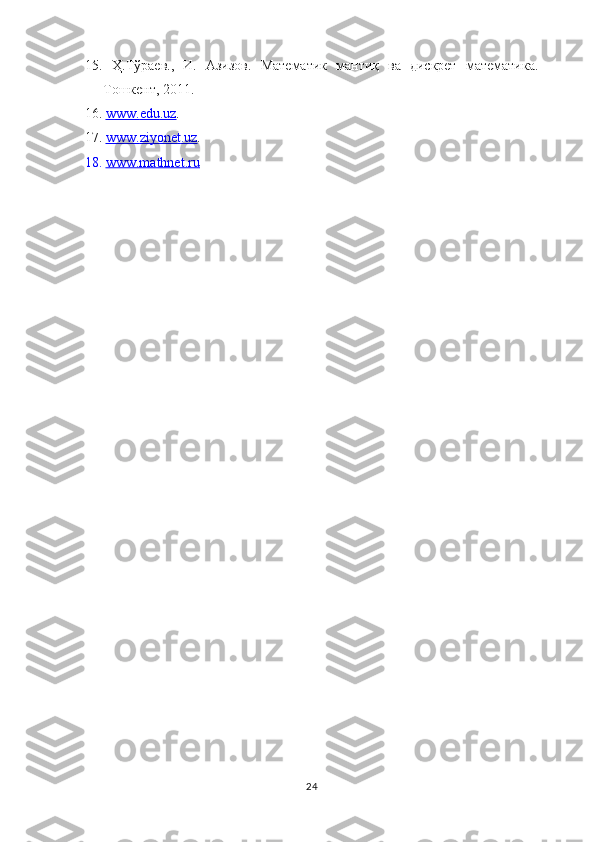
2.4. Deykstra algoritmning so’zli tavsifi .
Deykstra eng qisqa yo'l algoritmi . Deykstra algoritmi barcha tugunlarning
berilgan start tugunidan eng qisqa masofasini topish uchun ishlatiladi. U
mantiqiy ravishda bitta manba tugunidan eng qisqa yo'l daraxtini yaratadi,
tugunlarni ochko'zlik bilan qo'shib turing, shunda har bir nuqtada daraxtning har
bir tuguni berilgan boshlash tugunidan minimal masofaga ega bo'lad.
` Eng qisqa masofani topish masalalarni yechish uchun Deykstra algoritmi
ancha qulay va yahshi deb topilgan.
10](/data/documents/8fcceb4f-45fc-41d8-879b-10efb35a3028/page_10.png)



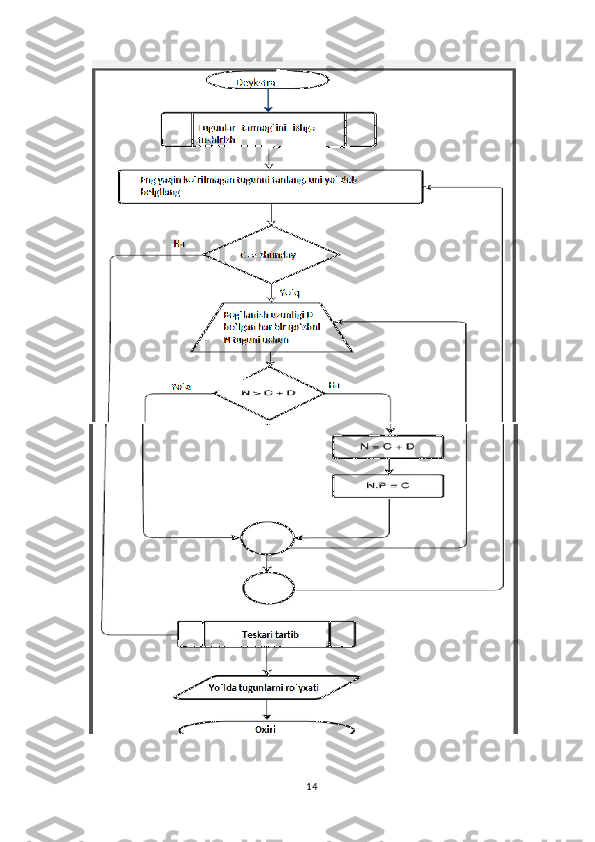


![C++ dastur kodi
Quyidagi algoritmda kodi u ning vertex'si min dist [u] ga teng, u vertex
majmuasida eng kam dist [u] qiymati bo'lgan vertex u ni izlaydi. uzunligi (u, v)
ikki qo'shni n-tugunni u va v o'rtasidagi chegara uzunligini qaytaradi. 18-satrda
o'zgaruvchining pastki qismi - ildiz tugunidan qo'shni tugunga yo'lning uzunligi
v U orqali o'tish kerak edi. Ushbu yo'l v uchun saqlangan joriy qisqa yo'ldan
qisqartirsa, u joriy yo'l bu pastki yo'l bilan o'zgartiriladi. Avvalgi qator manbaga
eng qisqa yo'lni olish uchun manba grafasida "keyingi-hop" tuguniga ko'rsatgich
bilan to'ldiriladi.
С++ dasturlash tilida quyidagicha bo’ladi:
#include<bits/stdc++.h>
#define INF INT_MAX
using namespace std;
// Function to find the non-visited node which is at minimum distance
int findMin ( int n, int cost [] , bool visited []){
int min=INF;
int node=0;
for ( int i=0;i < n;i++ ){
if ( visited [ i ] == false && min > cost [ i ]){
min=cost [ i ] ;
node=i;
}
}
return node;
}
void dijkstra ( int n, vector < pair < int , int >> graph [] , int start ){
17](/data/documents/8fcceb4f-45fc-41d8-879b-10efb35a3028/page_17.png)
![bool visited [ n ] ; // to specify which nodes are yet to visit
int cost [ n ] ; // cost[i] specifies the minimum cost to reach ith node from start node through visited
nodes
for ( int i=0;i < n;i++ ){
cost [ i ] =INF; // initialize cost array with INFINITY
// to signify that all nodes are non-reachable initially
visited [ i ] = false ; // initialize visited array with false
// to signify that all nodes are non-visited initially
}
cost [ start ] =0; // minimum cost to reach the start node will be zero
int count=0; // count will keep track of how many nodes are visited till now
while ( count < n ){
int node = findMin ( n,cost,visited ) ;
visited [ node ] = true ;
for ( auto &i:graph [ node ]){
if ( visited [ i. first ] == false ){
cost [ i. first ] = min ( cost [ i. first ] ,cost [ node ] + ( i. second )) ;
}
}
count++;
}
for ( int i=0;i < n;i++ ){
cout << "Distance of node " << i << " from node " << start << " is " << cost [ i ]<< "\n" ;
}
}
int main (){
int n,e;
18](/data/documents/8fcceb4f-45fc-41d8-879b-10efb35a3028/page_18.png)
![cin >> n >> e;
vector < pair < int , int >> graph [ n ] ;
for ( int i=0;i < e;i++ ){
int u,v,w;
cin >> u >> v >> w;
graph [ u ] . push_back ( make_pair ( v,w )) ;
graph [ v ] . push_back ( make_pair ( u,w )) ;
}
int start;
cin >> start;
dijkstra ( n,graph,start ) ;
}
Kiruvchi ma’lumotlar
Input:
4 5
0 1 12
0 3 24
2 0 3
1 3 10
3 2 12
0
Chiquvchi ma’lumotlar
Output:
Distance of node 0 from node 0 is 0
Distance of node 1 from node 0 is 12
Distance of node 2 from node 0 is 3
Distance of node 3 from node 0 is 15
6.Tegishli muammolar va algoritmlar.
Dijkstra original algoritmining funktsiyalari turli modifikatsiyalar bilan
kengaytirilishi mumkin. Masalan, ba'zida matematik jihatdan maqbul bo'lmagan
echimlarni taqdim etish maqsadga muvofiqdir. Kamdan-kamroq optimal
19](/data/documents/8fcceb4f-45fc-41d8-879b-10efb35a3028/page_19.png)




“Graflarda eng qisqa masofani topish algoritmlari” mavzusidagi Reja: I. Kirish II. Asosiy qism 1. Asosiy tushuncha 2. Eng qisqa masofani toppish algoritmlari 3. Floyd algoritmi 4. Deykstra algoritmi III. Xulosa IV. Foydalanilgan adabiyotlar 1
KIRISH Algoritmlarning turli ta’riflari mavjud. Rasmiy ta’riflardan biri bo’yicha algoritm bu qo’yilgan masalani bir xil yechilishiga olib keluvchi aniq harakatlarning ketma-ketligi. Bu tushunchadan algoritmning quyidagi xossalari kelib chiqadi: 1. Diskretlilik – ya’ni aniqlanayotgan jarayonni qadamba-qadam ko’rinishi. 2. Ommaviylik – algoritm o’xshash masalalar turkumini yechishi kerak. 3. Tushunarlilik – algoritmda beriladigan ko’rsatmalar foydalanuvchiga tushunarli bo’lib, uning talablariga javob berishi kerak. 4. Aniqlilik – algoritmda ma’lum tartibda amallarni bajarish nazarda tutilishi kerak va bajaruvchiga joriy qadam tugatilishi bilan qaysi qadam keyingi bo’lib bajarilishi aniq ko’rsatilishi kerak. Algoritmlar rasmiy ravishda bajariladi, bu degani bajaruvchi bajarilayotgan amallarni mazmunini anglash shart emas. Algoritm tuzish jarayoniga algoritmlashtirish deyiladi. Algoritm tuzish jarayonida nazariy va amaliy nuqtai nazardan algoritmlash, dasturlash va EHM larni qo’llash bilan bog’liq bo’lgan bilimlar kerak. Asosiy maqsad bu masalani qo’yish, masalaning yechish algoritmini tuzish, algoritmi mashina dasturi ko’rinishida amalga oshirish va algoritmni samaradorligini ko’rsatish muammolarini o’rganish. Bu jarayonlar algoritmni to’liq yaratish tushunchasiga olib keladi va quyidagi bosqichlarni belgilaydi: 1. Masalaning qo’yilishi. 2. Modelni yaratish. 3. Algoritmni ishlab chiqish. 4. Algoritm to’g’riligini tekshirish. 5. Algoritmni amalga oshirish. 6. Algoritmni va ularning murakkabligini tahlil qilish. 7. Dasturni tekshirish. 8. Hujjatlashtirish. 2
2.1Asosiy tushuncha. Qandaydir masalani xal etishga kirishishdan avval buning uchun eng yaxshi uslub izlanadi va uni qay tarzda tavsiflash aniqlanadi. Boshqacha qilib aytganda, biz doimo maqsadi ba’zi bir zaruriy natijaga erishishdan iborat, amallar ketma-ketligi bilan berilgan turli-tuman qoidalarga duch kelamiz. Bunday amallarning ketma-ketligi algoritm deb ataymiz. Matematikada algoritmning murakkabligi, xal etish masalalari va ularni ishlab chiqish prinsiplarini o‘rganadigan maxsus “Algoritmlar nazariyasi” bo‘limi xam mavjud. Algoritmlar nazariyasi – algoritmlarning umumiy xossalari, qonuniyatlari va ularni tasvirlanishining turli-tuman formal modellarini o‘rganish bilan shug'ullanadi. Algoritm tushunchasini formallashtirish asosida ularning samaradorligi taqqoslash, ularning ekvivalentligi tekshirish, qo‘llanilish sohasini aniqlash mumkin. Graflar nazariyasining asosiy masalasi berilgan nuqtalar va ularni tutashtiruvchi chiziqlarning xossalaridan tashkil topadi. Bunday talqinda chiziqlarnig to’g’ri chiziq yoki kesma, yoylardan yoki egri chiziqlardan iborat bo’lishi hamda bu chiziqlar qaerda joylashishi, uzun yoki qisqa bo’lishi muhim emas. Shunisi muhimki bu chiziqlar berilgan ikki nuqtani tutashtiradi. 1736 – yilda L.Eyler tomonidan o’sha davrda qiziqarli amaliy masalalardan biri hisoblangan Kyonisberg ko’priklari haqidagi masalaning qo’yilishi va echilishi graflar nazariyasining paydo bo’lishiga asos bo’ldi. Kyonisberg shaxridagi Pregel daryosi ustiga qurilgan yitita ko’prik o’sha vaqtda shaxarni to’rtta qismga ajratgan. Shaxarning ixtiyoriy qismida joylashgan uydan chiqib yitita ko’rikdan faqat bir martadan o’tib, yana o’sha uyga qaytib kelish mumkinmi? Kyonisberg ko’priklari haqidagi bu masalani hal qilish jarayonida graflarda maxsus marshrut (hozirgi vaqtda graflar nazariyasida bu marshrut Eyler tsikli nomi bilan yuritiladi) mavjudligi shartlari ham topildi. L.Eyler tomonidan e’lon qilingan tarixiy ilmiy ish yuz yildan kuproq vaqt mobaynida graflar nazariyasi bo’yicha 3
yagona ilmiy ish bo’lib keldi. XIX-asrning o’rtalarida graflar nazariyasi bilan bog’liq tadqiqotlar G.Kirxgof (1924–1887, olmon fizigi) va A.Keli (1821– 1895, ingliz matematigi) ishlarida paydo bo’ldi. “Graf” iborasi D.Kyonig (1884– 1944, venger matematigi) tomonidan 1936– yilda graflar nazariyasiga bag’ishlangan dastlabki darsliklarda uchraydi. Graflar nazariyasi bo’yicha tadqiqotlar natijalari inson faoliyatining turli sohalarida qo’llaniladi. Ulardan ba’zilari quyidagilar: boshqotirmalarni hal qilish; qiziqarli o’yinlar; yo’llar, elektr zanjirlari, integral sxemalari va boshqarish sistemalarini loyihalashtirish va hakazo. Avvalo grafning abstrakt matematik tushuncha sifatidagi ta’rifini keltiramiz. Ixtiyoriy nuqtalarning qandaydir usulda bog’lanishidan tashkil topgan V to’plamni qaraymiz. Ushbu V to’plamni uchlar to’plami va uning v∈V− elementlarini esa uchlar deb ataymiz. V to’plamning v1∈V va v2∈V elementlaridan tuzilgan (v1,v2) ko’rinishidagi barcha juftliklar to’plamini ( V to’plamning o’z-o’ziga Dekrat ko’paytmasini) V× V deb belgilaymiz. Graf deb shunday (V ,U ) juftlikga aytiladiki, bu erda V ≠ O va U − (v1,v2) ko’rinishidagi juftliklar bo’lib, V× V to’plamning elementlaridan tuzilgandir. Grafni lotin alifbosining G harfi bilan belgilaymiz. Grafga ta’rif berishda boshqacha yondoshuvdan ham foydalanish mumkin. G = G (V ) graf deb bir qancha V uchlar to’plamining birlashmasiga yoki E=(a,b)(a,b∈V ) (1.1) qaysi uchlar bog’langanligini ko’rsatuvchi juftliklarga aytiladi.Mos ravishda grafning geometrik tasvirida aniq har bir (1.1) juftlik grafning qirrasi deyiladi, a va b uchlar esa E qirraning oxirlari deyiladi. Qirraning (1.1) ta’rifida uning oxirgi ikki uchining joylashish tartibi e’toborga olinishi ham, olinmasligi ham mumkin. Agar bunday tartib mavjud bo’lmasa, ya’ni E = (a,b )= (b,a) deyish mumkin bo’lsa, u holda E ni yo’naltirilmagan qirra deb ataladi. Agar bunday tartib mavjud bo’lsa, u holda qirra yo’naltirilgan qirra deyiladi. Yo’naltirilgan E = (a,b ) qirrada a boshlang’ich uch, b oxirgi 4
uch deb hisoblanadi. Shuningdek E qirrani a uchdan chiquvchi va b uchga boruvchi qirra deyiladi. Qirra yo’naltirilgan bo’lgan holda ham, yo’naltirilmagan holda ham E= (a,b) qirra a va b uchlarga intsidient deb ataladi. Grafni yo’naltirilmagan deyiladi, agar uning barcha qirralari yo’naltirilmagan bo’lsa (1.1.a–rasm), yo’naltirilgan deyiladi agar barcha qirralari yo’naltiriligan bo’lsa (1.1.b– rasm). 1.1.a–rasm 1.1.b–rasm. Ham yo’naltirilgan, ham yo’naltirilmagan qirralarga ega bo’lgan graf aralash graf deyiladi. Misol sifatida, shaxarning xaritasini graf sifatida olsak, unda ko’chalarni qirra deb, chorrahalarni esa uchlar sifatida olish mumkin. Bunda faqat bir tomonlama harakat mavjud ko’chalarni yo’nalishga ega qirra deb olsak, u holda ikki tomonlama harakat mavjud ko’chalarni hech qanday yo’nalish orqali belgilab bo’lmaydi. Hech bir qirraga intsidient bo’lmagan uch yakkalangan uch deyiladi. Agar grafning ikkita uchini tutashtiruvchi qirra bor bo’lsa, u holda bunday uchlar qo’shni uchlar deyiladi, aks holda esa qo’shni bo’lmagan uchlar deyiladi.Faqat yakkalangan uchlardan tashkil topgan grafni nol graf deyiladi va 0 orqali belgilanadi. Ikkita chetki ya’ni boshlang’ich va oxirgi qirralari ustma-ust tushga qirra sirtmoq deyiladi va uni L= (a,a) kabi yoziladi (1.2–rasm). Agar rafning ikiita uchi o’zaro bir necha qirralar orqali tutashgan bo’lsa bunday qirralarni parallel yoki karrali qirralar deyiladi (1.3– rasm). Bunda agar graf yo’naltirilgan bo’lsa, hr bir qirra uchun yo’nalish aniqlanadi. Misol sifatida, jamoaviy musobaqani olish mumkin. Bunda jamoalar mos ravishda grafning uchlari hisoblanadi. Ikkita А va В jamoalar har safar 5
