Iqtisodiy indekslar Reja: 1.        Iqtisodiy  indekslarning  mohiyati  va  ahamiyati. 2.         Iqtisodiy  indekslarni  tasniflari. 3.         Individual  indekslar  – nisbiy  miqdorlar  sifatida. 4.         Umumiy  indekslar,  ularning  o’ziga  xos  xususiyatlari  va  tuzish   printsiplari. 5.        Agregat  indekslarni  tuzishda  vazn  tanlash  masalasi.  Laspeyres  va Paashe  indekslari.

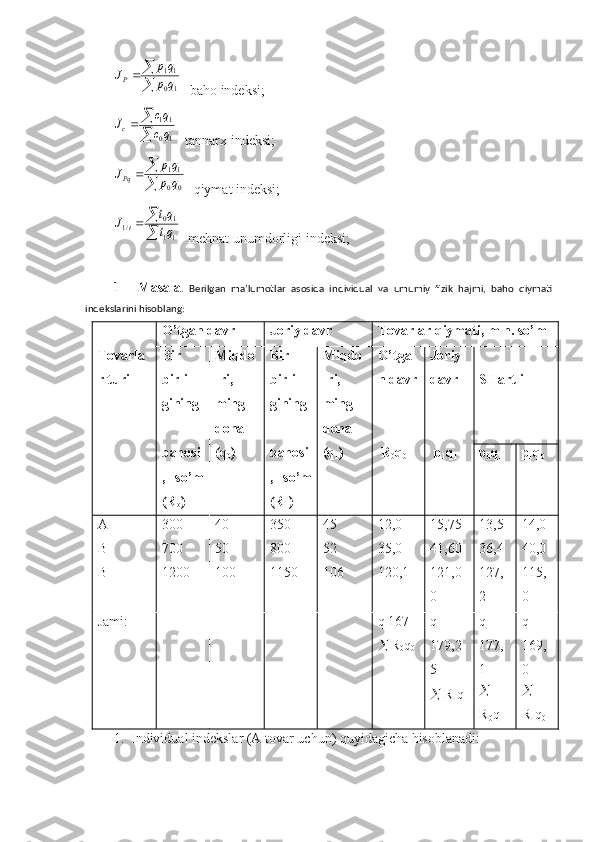
Indeks so’zi lotincha "indeks" atamasidan olingan bo’lib, belgi, ko’rsatkich degan ma’nolarni bildiradi. Statistikada indekslar deganda mahsus iqtisodiy ko’rsatkichlar tushuniladi. Ular iqtisodiy hodisa va jarayonlarni o’rganishda muhim ahamiyatga ega. Iqtisodiy indekslar bevosita umum o’lchovga ega bo’lmagan murakkab iqtisodiy hodisa va jarayonlarni o’rganishda muhim ahamiyatga ega. Iqtisodiy indekslar bevosita umum o’lchovga ega bo’lmagan murakkab iqtisodiy hodisa va jarayonlarning vaqt bo’yicha o’rtacha o’zgarishini ob’ektlararo yoki hududlararo taqqoslash natijasini ifodalaydi. Indekslar yordamida shuningdek shu hodisa va jarayonlarning o’zgarishiga ta’sir etuvchi omillarning roli va hissasi ham baholanadi. Indekslar murakkab hodisaning ayrim birliklari uchun ham va umuman murakkab hodisa uchun ham hisoblanish mumkin. Ular individual (alohida) va umumiy indekslarga bo’linadi. To’plamning ayrim birliklari uchun hisoblangan indekslar individual, barcha to’plam uchun hisoblangan indekslar esa umumiy (agregat) indekslar deb ataladi. Asosiy individual indekslar quyidagilardan iborat:0 1 q q ip - ishlab chiqarilgan yoki sotilgan mahsulotning fizik hajmi indeksi; 0 1 p p i p  - baho indeksi; 0 1 c c ic - tannarx indeksi; 0 0 11 q p qp ipq  - qiymat (tovar oboroti) indeksi; 1 0 /1 tt it  - mehnat unumdorligi indeksi . Umumiy indekslar quyidagilardan iborat:    0 0 10 q p q p Jq - fizik hajm indeksi;

   10 11 q p qp JP- baho indeksi;    10 11 qc qc Jc - tannarx indeksi;    0 0 11 q p qp JPq - qiymat indeksi;    11 10 /1 qt qt J t - mehnat unumdorligi indeksi; 1 - Masala . Berilgan ma’lumotlar asosida individual va umumiy fizik hajmi, baho qiymati indekslarini hisoblang: O’tgan davr Joriy davr Tovarlar qiymati, mln. so’m Tovarla r turi Bir birli- gining Miqdo -ri, ming dona Bir birli- gining Miqdo -ri, ming dona O’tga n davr Joriy davr SHartli bahosi , so’m (R o ) ( q 0 ) bahosi , so’m (R 1 ) (q 1 ) R 0 q 0 p 1 q 1 p 0 q 1 p 1 q 0 A B B 300 700 1200 40 50 100 350 800 1150 45 52 106 12,0 35,0 120,1 15,75 41,60 121,0 0 13,5 36,4 127, 2 14,0 40,0 115, 0 Jami: - - - - q 167  R 0 q 0 q 179,2 5  R 1 q 1 q 177, 1  R 0 q 1 q 169, 0  R 1 q 0 1. Individual indekslar (A tovar uchun) quyidagicha hisoblanadi:

Baho 116,6% ёки 166,1 900 350 01    p p iA p Fizik hajmi 112,5% ёки 125,1 40 45 01    q q iA p Qiymat 131,25% ¸êè 3125,1 0, 12 75, 15 0 0 11    q p qp i qpq Demak, A tovar uchun joriy davrda o’tgan davrga nisbatan baho 16,6% ga, fizik hajm 12,5 % ga va qiymat 31,25 % ortgan. 2. Umumiy indekslar quyidagicha hisoblanadi: % 106 ёки 06,1 0, 167 1, 177 0 0 1 0      q P q P JP % 101,14 ёки 0114,1 1, 177 25, 179 1 0 11      q P qP JP % 107,33 ёки 0733,1 0, 167 25, 179 0 0 11      q P qP JPq Demak, uchchala tovar bo’yicha joriy davrda o’tgan davrga nisbatan fizik hajm o’rtacha 6% ga, baholar 1,14% ga va qiymat esa 7,33% oshgan. O’rtacha indekslar. Statistikada umumiy indekslardan tashqari o’rtacha indekslar ham keng qo’llaniladi. O’rtacha indeksni o’rtacha arifmetik yoki o’rtacha garmonik ko’rinishda tuzish mumkin. O’rtacha indeksni qaysi shaklda hisoblashdan qat’iy nazar agregat indeks bilan birdek natija beradi. O’rtacha indeks umumiy indeksdan keltirilib chiqarilishi kerak. Buning uchun umumiy indeksning sur’ati yoki mahrajidagi indekslashtirilayotgan ko’rsatkichni uning individual indeksidan keltirilib chiqarilgan ayniyat qiymati bilan almashtirish lozimdir:       0 0 0 0 0 0 10 q P qPi q P qPi J p p P Demak, mahsulot fizik hajmi o’rtacha arifmetik indeksi individual indekslarni bazis davrdagi mahsulot qiymatlari bilan tortib olib o’rtacha arifmetik miqdor formulasi bilan aniqlanadi: 2 - Masala. quyidagi ma’lumotlar berilgan: Tovarlar Bazis davrdagi Joriy davrda bazis q 1

tovarooborot (mln.so’m) davrga nisbatan mahsulot hajmining o’zgarish, % i q q ------- q 0 A B 100,0 30,0 +4 +10 1,04 1,10105,3% ёки 053,1 130 137 130 33 104 30 100 30 10,1 100 01,1 0 0 0 0             q P q Pi J p P Demak, joriy davrda o’tgan davrga nisbatan Ava V tovarlari uchun o’rtacha fizik hajmi 5,3% ga oshgan. Agarda umumiy indeks mahrajidagi indekslashtirilayotgan miqdori (r 0 ), ayniyatga asoslanib, uning teng qiymati bilan almashtirsak, u holda umumiy indeksimiz o’rtacha garmonik indeksga aylanadi: p pp i P P P i Pq Pq Pq Pq J 1 0 01 p 11 11 01 11 P ва i ердабу     3 - Masala. Savdo shahobchasi bo’yicha quyidagi ma’lumotlar berilgan. Tovar guruhlari Joriy davr tovarooboroti, (mln. so’m) Baholarning pasayishi, % da Individual, baho indeksi, i r qr 1 /r 0 Gazmollar Tayyor kiyimlar Galantereya 350 800 60 1 4 6 0,99 0,96 0,94 I p q350+800+60/((350/0,99)+(800+0,96)+(60/0,94))q0,967 yoki 96,7 % Demak, uchchala tovar guruhlari bo’yicha joriy davrda o’tgan davrga nisbatan baholar o’rtacha 3,3 % ga pasaygan (100 - 96,7 q3,3) O’rtacha ko’rsatkichlar dinamikasini faqat o’rtalashtirilayotgan belgining o’zgarishini ko’rsatish bilan cheklanmay ushbu to’plam tarkibi o’zgarishini ifodalashni ham taqozo qiladi. Buni o’rganish uchun o’zgaruvchan, o’zgarmas tarkibli va tuzilma siljish indekslaridan foydalanamiz: a) o’zgarmas tarkibli baho indeksi: