ZO‘RIQQAN HOLAT DIAGRAMMASI

ZO‘RIQQAN HOLAT DIAGRAMMASI Reja: 1. Chiziqli zo‘riqish holatida qiya yuzachalar bo‘yicha kuchlanishlar. 2. Tekis kuchlanganlik holatida qiya tekisliklar bo’yicha kuchlanishlar. 3. Hajmiy zo‘riqqan holatdagi qiya yuzachalar bo‘yicha kuchlanishlar. 4. Hajmiy va tekis zo‘riqish holatidagi deformatsiyalar va kuchlanishlar orasidagi bog‘liqlik.
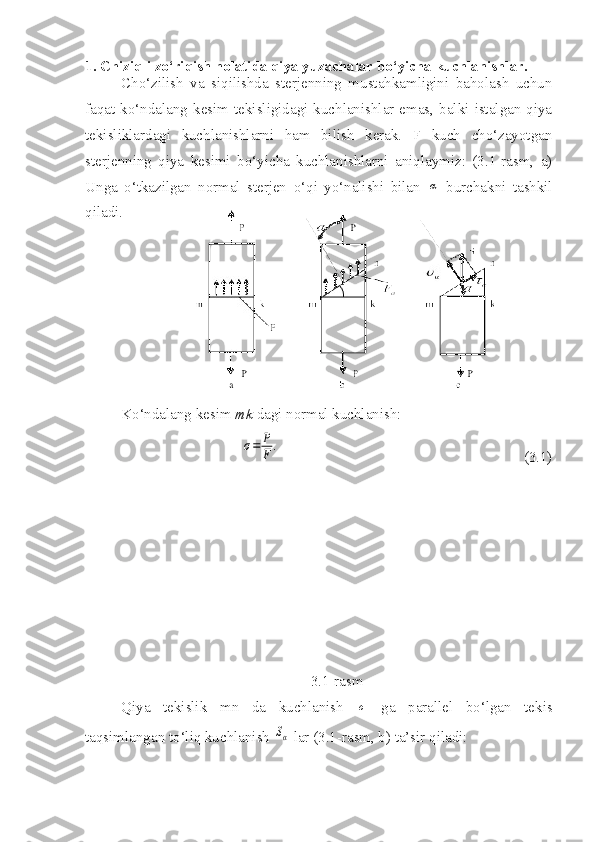
1. Chiziqli zo‘riqish holatida qiya yuzachalar bo‘yicha kuchlanishlar. Cho‘zilish va siqilishda sterjenning mustahkamligini baholash uchun faqat ko‘ndalang kesim tekisligidagi kuchlanishlar emas, balki istalgan qiya tekisliklardagi kuchlanishlarni ham bilish kerak. F kuch cho‘zayotgan sterjenning qiya kesimi bo‘yicha kuchlanishlarni aniqlaymiz: (3.1-rasm, a) Unga o‘tkazilgan normal sterjen o‘qi yo‘nalishi bilan α burchakni tashkil qiladi. Ko‘ndalang kesim mk dagi normal kuchlanish: σ= P F . (3.1) 3.1-rasm Qiya tekislik mn da kuchlanish σ ga parallel bo‘lgan tekis taqsimlangan to‘liq kuchlanish Sα lar (3.1-rasm, b) ta’sir qiladi:
Sα= P Fα . (3.2) Qiya tekislik yuzasi Fα= F cos α bo‘lgani uchun: Sα= P cos α F = σ⋅cos α . (3.3) Biror nuqtadagi to‘liq normal yo‘nalishga va qiya tekisligiga proeksiyalab (3.1-rasm, c), shu kesimdagi normal va urinma kuchlanishlarni aniqlash formulalarini hosil qilamiz: σα= Sαcos α= σcos 2α (3.4) τα= Sαsin α= σcos α⋅sin α= σ 2sin 2α . (3.5) Kuchlanishlar qiymati α burchakning vaziyatiga bog‘liq. Eng katta normal kuchlanishlar sterjenning ko‘ndalang kesimida ta’sir qiladi: α= 0 da kuchlanish σαmax = σ , urinma kuchlanish τα=0 . Agar α=90 ∘ bo‘lsa, kuchlanishlar σα= 0 va τα=0 , ya’ni sterjenning bo‘ylama kesimlarida normal va urinma kuchlanishlar bo‘lmaydi. Asosiy kuchlanishlar cho‘zilishda σ1= σ , σ2= 0 va σ3=0 , siqilishda σ1= 0,σ2= 0 va σ3=− σ . Urinma kuchlanishlar sterjen o‘qiga α= 45 ∘ burchak ostida yotgan qiya tekislikda eng katta qiymatga erishadi. sin 2α=1 bo‘lgani uchun: ταmax = σ 2. (3.6) Agar normal kuchlanish cho‘zuvchi bo‘lsa musbat, siquvchi bo‘lsa manfiy bo‘ladi. Chiziqli zo‘riqish holatidagi elementning ikki o‘zaro perpendikulyar yuzachalarida normal va urinma kuchlanishlarni topamiz (3.2-rasm). σ1= σ ni hisobga olib, quyidagilarni hosil qilamiz: σα= σ1cos 2α va τα= σ1 2 sin 2α (3.7) va (3.8)
β= α+90 ∘ burchak ostida qiya yotgan yuzachada quyidagilarni hosil qilamiz: σβ= σ1cos 2β= σ1cos 2(α+90 ∘)= σ1sin 2α (3.9) τβ= σ1 2 sin 2β= σ1 2 sin 2(α+90 ∘)= − σ1 2 sin 2α (3.10) Normal kuchlanishlar formulalarini qo‘shib, ushbuni topamiz: σα+σβ= σ1cos 2α+σ1sin 2α= σ1 (3.11) 3.2-rasm ya’ni ikki o‘zaro perpendikulyar yuzachalarda normal kuchlanishlar yig‘indisi o‘zgarmas va asosiy kuchlanishga teng. Urinma kuchlanishlar formulalarini qiyoslasak: τα=−τβ (3.12) ya’ni ikki o‘zaro perpendikulyar yuzachalarda urinma kuchlanishlar qiymati jihatidan teng va ishora jihatidan qarama-qarshiligi kelib chiqadi. Bu xossa kuchlanishlarning juftlik qonunu deb ataladi. 2. Tekis kuchlanganlik holatida qiya tekisliklar bo’yicha kuchlanishlar.
