Ko'rsatkichli tenglamalar

![, 0
) (
) (
x Q
x P ]. [ , x R Q P
. 0 ) (
, 0 ) (
0
) (
) (
x Q
x P
x Q
x PAlgebraik t englama v a
uning y echilish sxemasi
, 0
) (
) (
x Q
x P ]. [ , x R Q P
. 0 ) (
, 0 ) (
0
) (
) (
x Q
x P
x Q
x P](/data/documents/55cae6a4-4a8c-4231-a7a7-62a2adc0f1fe/page_2.png)
















Ko’rsat k ichli t e nglamalar
, 0 ) ( ) ( x Q x P ]. [ , x R Q P . 0 ) ( , 0 ) ( 0 ) ( ) ( x Q x P x Q x PAlgebraik t englama v a uning y echilish sxemasi , 0 ) ( ) ( x Q x P ]. [ , x R Q P . 0 ) ( , 0 ) ( 0 ) ( ) ( x Q x P x Q x P
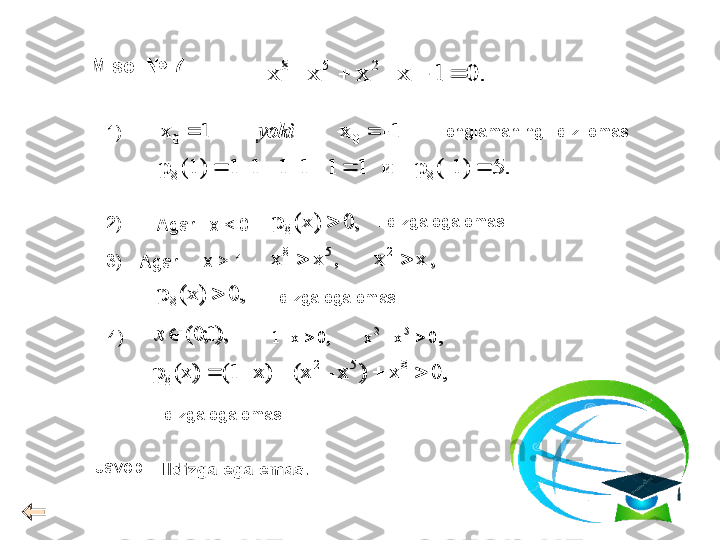
Misol № 1 .*)1( . 1 1 1 2 2 x x x . 0 , 0 )1 ( ;0 , 0 0 0 )1 ( 1 0 1 1 1 *)1( 2 2 2 2 2 2 2 2 x x x x x x x x x x x x x x x . 1 x Javob : .1 ;0 ,1,0 x x xx *)1( . 1 1 1 2 2 x x x . 0 , 0 )1 ( ;0 , 0 0 0 )1 ( 1 0 1 1 1 *)1( 2 2 2 2 2 2 2 2 x x x x x x x x x x x x x x x . 1 x .1 ;0 ,1,0 x x xx
p (x) = 0 ko’rinishdagi tenglamalar . 1 . Chiziqli tenglama . 2. Kvadrat Tenglama 3. Ixtiyoriy darajadagi ikki o’zgaruvchili tenglamalar. 4. Bikvadrat tenglamalar.nn
1) Chiziqli tenglama ( darajasi n =1) : 2) Kvadrat tenglama ( n =2):. )0 ( ,0 a b x b ax a b ax , ) 0 ( 0 2 a c bx ax . 4 2 ac b D Agar D < 0 Agar D = 0 Agar D > 0 a b x 2 0 a ac b b x 2 4 2 2.1 Ildizi yo’q . )0 ( ,0 a b x b ax a b ax , ) 0 ( 0 2 a c bx ax . 4 2 ac b D a b x 2 0 a acbb x 2 4 2 2.1
