vektorlar ustida amallar




Vek t orlar ust ida amallar
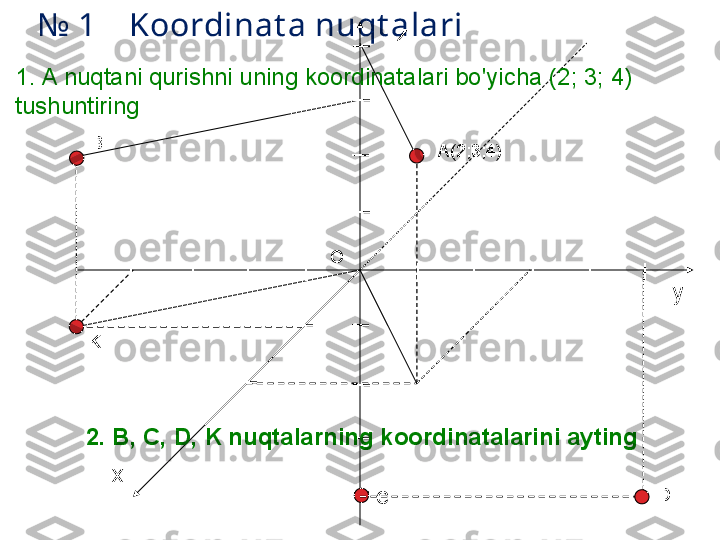
№ 1 Koordinat a nuqt alari A(2;3;4)z x yO || | ||| | | || | | | | | | | | |1. A nuqtani qurishni uning koordinatalari bo'yicha (2; 3; 4) tushuntiring 2. B, C, D, K nuqtalarning koordinatalarini ayting B C DK
№ 2. Koordinatalari berilgan vektorlar ustida amallar kzzjyyixx kzjyiхkzjyiхba zyxmma zzyyxxddba zzyyxxccba zyxbzyxa zyxakzjyiха 212121 222111 111 212121 212121 222111 ;;, ;;, ;;, ;;,;; ;;,
Berilgan vektorlar .3;1;2,2;5;0,0;2;1 cbа a b c q 2 3 Yechish Kordinata vektorlari 0; 2;1 , , 4; 10; 0 2 9 ; 3; 6 3 а b с zyxq ;; х = 6 + 0 – 1 = 5, у = 3 + 10 + 2 = 15, z = -9 + 4 + 0 = -5 5;15;5 q3. Koordinatalari berilgan vektorlar ustida amallar Vektor koordinatalarini toping
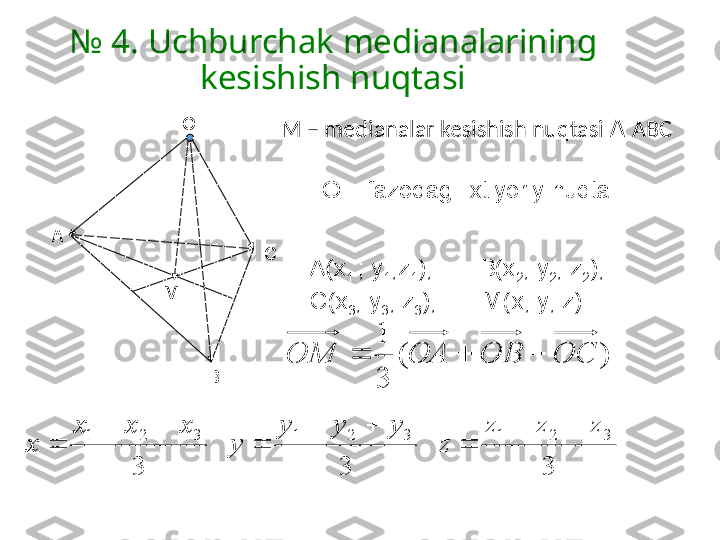
№ 4. Uchburchak medianalarining kesishish nuqtasi М – medianalar kesishish nuqtasi ∆ АВС) ( 3 1 ОС ОВ ОА ОМ 333 321321321 zzz zууу уххх х М O С ВА О – fazodagi ixtiyoriy nuqta А(х 1 ; у 1 ; z 1 ), В(х 2 ; у 2 ; z 2 ), C(x 3 ; y 3 ; z 3 ), M(x; y; z)
