C++ da vektorlarni skalyar ko`paytmasini topish modulini ishlab chiqarish









![C++ da vektorlarni skalyar ko`paytmasini topish moduli
C++ dasturlash tilida vektorlarning skalyar ko‘paytmasini (dot product)
hisoblash uchun modul yaratish uchun avvalo ikki vektorning elementlarini
o‘zaro ko‘paytirib, ularning yig‘indisini olish kerak.
Biz quyida, ushbu vazifani bajaradigan dastur kodini ko‘rib chiqamiz.
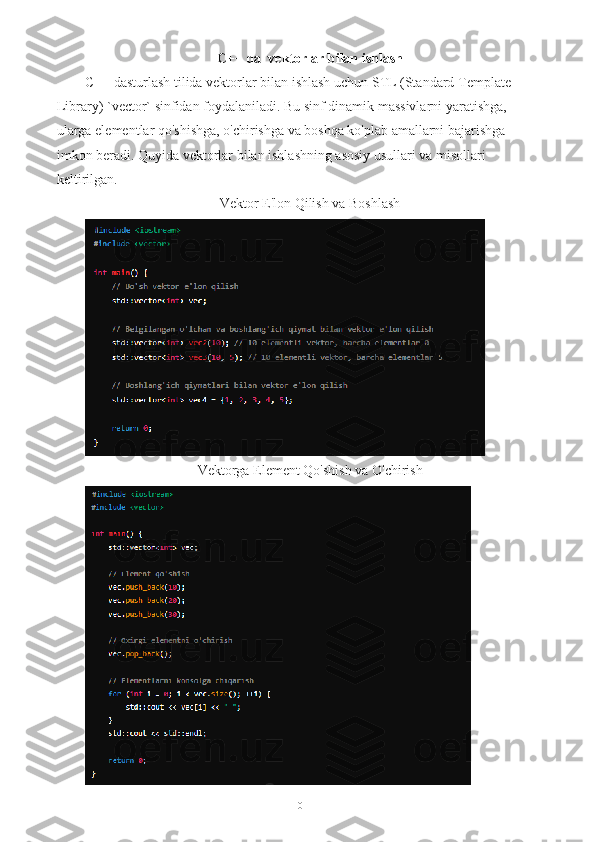
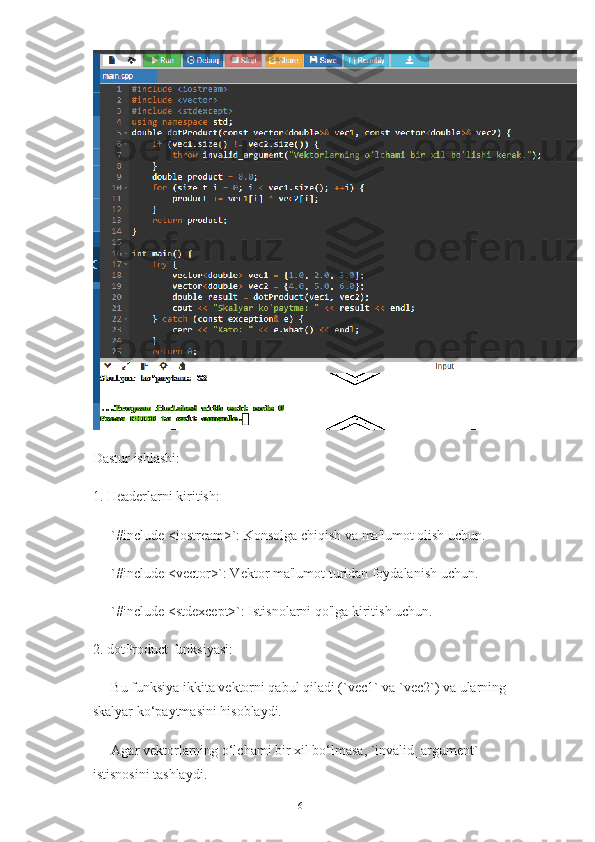
Dastur Kodi:
#include <iostream>
#include <vector>
#include <stdexcept>
using namespace std;
double dotProduct(const vector<double>& vec1, const
vector<double>& vec2) {
if (vec1.size() != vec2.size()) {
throw invalid_argument("Vektorlarning
o'lchami bir xil bo'lishi kerak.");
}
double product = 0.0;
for (size_t i = 0; i < vec1.size(); ++i) {
product += vec1[i] * vec2[i];
}
14](/data/documents/f43b9f73-0def-4c25-a1fd-38d0518e07f3/page_14.png)



![Foydalanilgan adabiyotlar
1. Жураев Т.Ж., Худойберганов Р.Х., Ворисов А.К., Мансуров Х., Олий
математика асослари. Дарслик. - Т.: Ўзбекистон, 1999. 290 бет. 2.Rajabov F.,
Masharipova S., Madrahimov R. Oliy matematika. T.: "TURON-IQBOL". 2007.
399b.
3. Fayzullayeva S.F. Ehtimollar nazariyasidan masalalar to'plami: o'quv
qo'llanma.-T.: O'zbekiston faylasuflari milliy jamiyati. 2006. 112-b.
4. Высшая математика для экономистов . Под редакций Н.Ш.Кремера М.:
ЮНИТИ, 2001, 601 ст.
5. Urdushev X., Usmonov R. Iqtisodiy matematik usullar va modellardan
amaliy mashg'ulotlar. Samarqand 2006
6. Urdushev X., Boychaqayev M. Matematik dasturlash fanidan ma'ruza,
amaliy, laboratoriya mashg'ulotlari va mustaqil ta'lim uchun uslubiy qo'llanma.
7. С. К. Ганиев. Электрон хисоблаш машиналари ва системалари. – Т
«Укитувчи» 1990.
8. Аmaliy matematika, dasturlash va kompyuterning dasturiy ta’minoti:
Оliy o’quv yurtlari uchun qo’llanma/ Т.Х. Хоlmatov, N.I. taylaqov -Т.: Меhnat,
2000.-304 b.
9. Hisoblash matematikasi va dasturlashdan laboratoriya ishlari: [Оliy
o’quv yurtlari uchun qo’llanma]. -Т.: O’qituvchi, 1993.-176 b.
10. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, va Clifford
Stein tomonidan yozilgan "Introduction to Algorithms" kitobi - Algoritmlar
nazariyasi va amaliyoti bo'yicha asosiy manba.
19](/data/documents/f43b9f73-0def-4c25-a1fd-38d0518e07f3/page_19.png)
MAVZU: C++ da vektorlarni skalyar ko`paytmasini topish modulini ishlab chiqarish. Reja I. Kirish II. Asosiy qism 1. Vektorlarni skalyar ko`paytmasini topish 2. C++ da vektorlar bilan ishlash. 3 C++ da vektorlarni skalyar ko`paytmasini topish moduli III. Xulosa IV Foydalanilgan adabiyotlar 1
Kirish Vektor nisbatan yangi matematik tushuncha hisoblanadi. «Vektor» terminining o‘zi 1845 yilda Vilyam Rouen Gamilton tomonidan kiritilgan 1 . Vektor tushunchasiga son qiymati va yo‘nalishi bilan xarakterlanuvchi ob’ektlar bilan ish ko‘rilganida duch kelinadi. Bunday ob’ektlarga kuch, tezlik, tezlanish kabi fizik kattaliklar misol bo‘ladi. Vektor matematikaning turli bo‘limlarida, masalan, elementar, analitik va differensial geometriya bo‘limlarida qo‘llaniladi. Vektorli algebra fizika va mexanikanig turli bo‘limlariga, kristallografiyaga, geodeziyaga tatbiq qilinadi. Vektorlarsiz nafaqat klassik matematika, balki boshqa ko‘plab fanlarni tasavvur qilib bo‘lmaydi. Vektorlar ustida qo‘shish va songa ko‘paytirish, amallarini, vektorlarning skalyar, vektor va aralash ko‘paytmalarini, vektorlarni baziz fazoda almashtirishni, vektorlarni proyeksiyalashni va shu kabi masalalarni o‘rganish vektorli algebraning predmeti hisoblanadi. Vektorlar, matematikada va kompyuter grafikasi kabi ko‘plab sohalarda keng qo‘llaniladi. Vektorlarning skalyar ko‘paytmasi (yoki dot product) ikki vektor orasidagi geometrik munosabatlarni aniqlashda muhim ahamiyatga ega. Skalyar ko‘paytma, ikki vektorning mos keluvchi elementlarini ko‘paytirib, ularning yig‘indisini olish orqali hisoblanadi. Bu amaliyot, ko‘plab ilmiy hisob-kitoblar va algoritmlarda qo‘llaniladi. Vektorlarning skalyar ko‘paytmasi nima? Ikki vektor a va b ning skalyar ko‘paytmasi, ularning mos elementlarini ko‘paytirib, yig‘indisini olish orqali aniqlanadi: a*b= ∑ ( a i * b i ) bu yerda a i va b i mos ravishda a va b vektorlarining i -chi elementlari, va n esa vektorlarning uzunligi. Skalyar ko‘paytmaning asosiy qo‘llanilish joylaridan biri, ikki vektor orasidagi burchakni aniqlash va vektorlarning ortogonal (perpendikulyar) bo‘lishini tekshirishdir. Agar ikki vektorning skalyar ko‘paytmasi nolga teng bo‘lsa, demak ular ortogonaldir. 2
C++ dasturlash tili, uning yuqori samaradorligi va kuchli standart kutubxonasi tufayli ilmiy va texnik hisob-kitoblar uchun keng qo‘llaniladi. STL (Standard Template Library) ning `vector` sinfi, dinamik massivlar bilan ishlashni osonlashtiradi va skalyar ko‘paytmani hisoblash uchun qulay vosita hisoblanadi. Vektorlarning skalyar ko‘paytmasini hisoblash moduli. Ikki vektorning skalyar ko‘paytmasini hisoblash moduli quyidagi talablarni qondirishi kerak: 1. Ikki vektorni qabul qilish: Funksiya ikkita vektor qabul qilishi kerak. 2. Vektorlarning uzunligini tekshirish: Funksiya, vektorlarning uzunligi bir xil ekanligini tekshirishi va agar bir xil bo‘lmasa, xatolik (exception) tashlashi kerak. 3. Skalyar ko‘paytmani hisoblash: Funksiya, ikki vektorning mos elementlarini ko‘paytirib, yig‘indisini qaytarishi kerak. 3
Vektorlarni skalyar ko`paytmasini topish 1. Fazo tushunchasi Fanda fazo tushunchasi har xil ma’nolarga ega. Fazoni filosofik talqin qiladigan bo’lsak, u materiyaning yashash shaklini anglatadi. Haqiqiy dunyoning fazoviy ko’rinishi undagi mikdoriy munosabatlar bilan birgalikda matematikaning o’rganiladigan predmeti bo’lib, bunda u geometriyaning bosh mazmunini tashkil qiladi. Maktab geometriyasida fazo tushunchasi sodda ko’rinishda uchraydi, fazo deganda ma’lum aksiomalar sistemasini qanoatlantiruvchi uch o’lchamli ( x, y, z ) haqiqiy sonlar uchligidan iborat nuqtalar to’plami tushuniladi. Fazoning har bir nuqtasi uchta koordinatalar orqali aniqlanadi va aksincha, har bir uchta sonlarning tartiblangan sistemasi fazoda qandaydir nuqtani aniqlaydi. Shunday qilib, uch o’lchamli fazoni uchta haqiqiy son sistemasi bo’lgan (x, y, z) nuqtalarning to’plami deb qarash mumkin. Bunda ikki A (x 1 , y 1 , z 1 ) B (x 2 , y 2 , z 2 ) nuqtalar orasidagi masofa formula bilan aniqlanadi. Fazo tushunchasi matematikada ancha murakkab tuzilishga ega bo’lgan ob’yektlar uchun umumlashtiriladi. Matematikada fazo deganda, ixtiyoriy ob’yektlar (sonlar to’plami, funksiyalar to’plami va h.k.) majmuasi tushuniladi va ular orasida uch o’lchamli fazoda o’rganilgan munosabatlarga o’xshash munosabatlar o’rnatiladi. Bunda ikki nuqta orasidagi masofa tushunchasi muhim o’rin egallaydi. 2. n-o’lchamli vektor fazo Geometriya, mexanika va fizikada shunday ob’yektlar uchraydiki, ular bir yoki bir necha haqiqiy sonning tartiblangan sistemasi bilan aniqlanadi. Masalan, (uch o’lchamli) fazoda har qanday vektor o’zining uchta komponentasi bilan aniqlanadi. Fazo tushunchasini umumlashtirish vektor tushunchasini umumlashtirish bilan bog’liq. Vektorning eng sodda umumlashtirilishi n-o’lchamli vektor tushunchasidir. 1-ta’rif . Tartib bilan yozilgan n ta haqiqiy son sistemasi (majmuasi), ya’ni a=(a 1 , a 2 ,. . .. . .. . ., a n ) n-o’lchamli vektor deyiladi. Bunda, a 1 , a 2 ,. . .. . .. . ., a n sonlar vektorning koordinatalari deyiladi. Kelajakda, vektorlarni a,b,c va h.k. lotin alifbosining harflari bilan, ularning koordinatalarini esa shu harflarning indekslari yordamida yozamiz. 4
2-ta’rif . Ikkita a=(a 1 , a 2 ,. . ., a n ) va b=(b 1 , b 2 ,. . ., b n ) vektorlarning mos koordinatalari teng, yani a 1 =b 1 , a 2 =b 2 ,. . . a n =b n bo’lsa, bu vektorlar teng deb ataladi. Bu ta’riflardan ko’rinadiki, vektor bu n -ta haqiqiy son to’plami bo’libgina qolmay, balki elementlari tartiblangan sistema hamdir. Berilgan vektorning koordinatalarini boshqa tartibda yozilsa, umumiy holda boshqa vektor hosil bo’ladi. Masalan, a= (1,2,3) va b= (2,3,1) vektorlar boshqa-boshqa vektorlardir. Misollar. 1. Tekislikdagi vektorlar ikki o’lchamli vektorga misol bo’ladi: a=(a 1 ,a 2 ), uch o’lchamli fazodagi vektorlar uch o’lchamli vektorga misol bo’ladi: a = (a 1 ,a 2 ,a 3 ) 2. Bir o’zgaruvchili (n-1) darajali f(x)=a 0 +a 1 x+. . .+a n-1 x n-1 ko’phadni n o’lchamli a = (a 0 ,a 1 ,... a n-1 ) vektor sifatida qarash mumkin. Endi, n o’lchamli vektorlar ustida chiziqli amalllar kiritamiz. 3-ta’rif . Ikki a=(a 1 , a 2 ,. . ., a n ) va b=(b 1 , b 2 ,. . .,b n ) vektorning yig’indisi deb a+b vektorga aytiladi va u quyidagicha aniqlanadi: a+b=(a 1 +b 1 a 2 +b 2 . . ., a n +b n ) 4-ta’rif . a=(a 1 , a 2 ,. . ., a n ) vektorning haqiqiy songa ko’paytmasi deb, a vektorga aytiladi va u quyidagicha aniqlanadi: a=( a 1 , a 2 , ... a n ) 5-ta’rif. Hamma koordinatalari nolga teng bo’lgan vektor nol vektor deyiladi va 0=(0, 0, . . ., 0) orqali yoziladi. Vektorlarni qo’shish va songa ko’paytirish amali vektorlar ustida chiziqli amallar deyiladi va ular quyidagi xossalarga ega bo’ladi: 1 0 . a+b=b+a (qo’shishning kommutativlik xossasi). 2 0 . (a+b)+c=a+(b+c) (qo’shishning assosiativlik xossasi). 3 0 . Ixtiyoriy a vektor uchun a+0=a tenglik o’rinli bo’ladi. 4 0 . Har bir a vektor uchun unga qarama-qarshi vektor deb ataluvchi –a vektor mavjud bo’lib, a+(-a)=0 bo’ladi. 5 0 . (a+b)= a+ b (ko’paytirishning qo’shishga nisbatan distributivlik xossasi) 6 0 1. a=a (har qanday vektor 1 songa ko’paytirilsa, shu vektorning o’zi hosil bo’ladi). 6-ta’rif. Ixtiyoriy a vektor bilan birga yo’nalishi a vektorga qarama-qarshi, moduli ga teng bo’lgan vektor, a vektorga qarama-qarshi vektor deb ataladi va – a bilan belgilanadi: - a =( -a 1 , -a 2 ,. . ., -a n ) . Ravshanki, a+(-a)=0 bo’ladi. 5
