EVOLYUTSION ALGEBRA VA UNING TADBIQLARI

Yuklangan vaqt:

20.11.2024

Ko'chirishlar soni:

0

Hajmi:

835.1650390625 KB

Ko'chirib olish

“ EVOLYUTSION ALGEBRA VA UNING TADBIQLARI ”
MUNDARIJA
Kirish………………………………………………………………………………3
I.BOB. UMUMIY TUSHUNCHALAR. GRUPPA, HALQA, MAYDON VA
VEKTOR FAZO TUSHUNCHALARI. ASSOSIATIV VA NOASSOSIATIV
ALGEBRALAR
1.1 - § . Gruppa, halqa va maydon…………………………………………….......5
1.2 - § . Vektor fazo va unga misollar…………………………………………...14
1.3 - § . Algebra tushunchasi. Assosiativ va noassasiativ algebralar……………18
II.BOB. GENETIK VA EVOLYUTSION ALGEBRALAR. ABSOLYUT
NILPOTENT VA IDEMPOTENT ELEMENTLAR
2.1 - § . Genetik va evolyutsion algebralar tarixi……………………………......21
2.2 - § . Evolyutsion algebralar va ularning xossalari…………………………...25
2.3 - § . Absolyut nilpotent va idempotent elementlar…………………………..31
III.BOB. EVOLYUTSION ALGEBRALARNING TADBIQLARI
3.1 - §. Evolyutsion algebraning biologiyaga tadbiqi………………..................33
3.2 - §. Evolyutsion algebraning fizikaga tadbiqi………………........................37
3.3 - §. Evolyutsion algebraning ehtimollar nazariyasiga tadbiqi……………...39
1. Xulosa ..........................................................................................................41
2. Foydalanilgan adabiyotlar ............................................................................42
1

KIRISH
Bitiruv malakaviy ishining dolzarbligi: Ushbu bitiruv malakaviy ishimda
zamonaviy algebraning keng o ‘ rganilayotgan sohalaridan biri bo ‘ lgan evolyutsion
algebra va uning tadbiqlari o ‘ rganilgan. Jumladan evolyutsion algebraning
xossalari, uning muhim elementlari hamda bu algebraning biologiya, fizika va
ehtimollar nazariyasiga tadbiqlari o ‘ rganilgan.
Bitiruv malakaviy ishining maqsadi: Evolyutsion algebraning xossalarini,
uning muhim elementlarini hamda uning fizikaga, biologiyaga va ehtimollar
nazariyasiga tadbiqlarini o ‘ rganishdan iboratdir.
Bitiruv malakaviy ishining vazifalari: Bitiruv malakaviy ishining vazifalari
evolyutsion algebraning xossalarini, uning muhim elementlarini o ‘ rganish va
ularning amaliy ahamiyatini izohlash, hamda evolyutsion algebraning fizikaga,
biologiyaga va ehtimollar nazariyasiga tadbiqlarini o’rganish, bu yo ‘ nalishga
qizziqgan va o ‘ rganishni istagan talabalar, magistrlar va yosh olimlar uchun o ‘ zbek
tilida yozilgan dastlabki muhim ma’lumotlar bazasini shakllantirishdan iborat.
Bitiruv malakaviy ishining o ‘ rganilganlik darajasi: Ushbu malakaviy
bitiruv ishida qo’yilgan talablar bajarildi, qo’yilgan vazifa yuzasidan ma’lumotlar
o ‘ rganildi va ularning o ‘ zbek tilidagi dastlabki namunasi shakllantirildi. Gruppa,
halqa va maydon haqidagi dastlabki muhim ma’lumotlar va ularga doir misollar,
vektor fazo va unga misollarni o ‘ rganishda Sh.A.Ayupov, B.A.Omirov,
A.X.Xudoyberdiyev “Abstrakt algebra” o ‘ quv qo ‘ llanmasidan, noassosiativ
algebralarni o ‘ rganishda Murray R. Bremner, Lucia I. Murakami, Ivan P.
Shestakovlarning “Nonassociative Algebras” nomli ilmiy asaridan, genetik va
evolyutsion algebralar tarixi, evolyutsion algebralar, hamda bu algebralarning
absolyut nilpotent va idempotent elementlarini o ‘ rganishda bu yo ‘ nalishda
fundamental ma’lumotlar bazasini o ‘ zida mujassamlashtirgan Jianjun Paul
Tianning “Evolution Algebras and their Applications” ilmiy asaridan,
J.M.Casas, M.Ladra, B.A.Omirov va U.A.Rozikovlarning “On Evolution
Algebras” nomli ilmiy maqolasidan, B.A.Narkuziyevning “ On absolute
2

nilpotent and idempotent elements of an evolution algebra corresponding to
permutations” nomli maqolasidan va “Evolution algebras and their three-
dimensional chains” nomli PhD dissertatsiya ishlari qaraldi. Evolyutsion
algebralarning tadbiqlari haqidagi asosiy ma’lumotlarni o ‘ rganishda Jianjun Paul
Tianning “Evolution Algebras and their Applications” ilmiy asariga
hamda U.A. Rozikovning “Population dynamics: algebraic and probabilistic
approach” (World Sci. Publ. Singapore, (2020), 460 pp) nomli ilmiy kitobiga
tayanildi [33].
Bitiruv malakaviy ishining ob’yekti: Ushbu ishning ob’yekti evolyutsion
algebraning xossalari, uning muhim elementlari va ularning amaliy ahamiyatini
izohlash, hamda evolyutsion algebraning fizika, biologiya va ehtimollar
nazariyasiga tadbiqlari o ‘ rganish, bu sohadagi dastlabki o ‘ zbek tilidagi ilmiy
ma’lumotlarni to ‘ plash va bu sohani o’rganishni boshlagan yosh olimlarga sohaga
kirish uchun fundamental ma’lumotlarni yetkazish hisoblanadi.
Bitiruv malakaviy ishining predmeti: Evolyutsion algebralarning paydo
bo ‘ lish tarixi, uning boshqa algebralardan farqi, uning xossalari va fanning turli
sohalariga tadbiqlarini o ‘ rganish, shu paytgacha bu sohada to ‘ plangan
ma’lumotlarni o ‘ zbek tilida o’quvchiga yetkazishdan iborat.
Bitiruv malakaviy ishida qo ‘ llanilgan metodikaning tavsifi: Ishda
chiziqli va abstrakt algebraning usullaridan, ilmiy tadqiqot ishlarini nazariy va
amaliy jihatdan bog ‘ lashning tayanch usullaridan, hamda noassosiativ algebralarni
o ‘ rganishning umumiy usullaridan foydalanilgan.
Bitiruv malakaviy ishi mundarija, kirish, uchta bob, xulosa va adabiyotlar
ro ‘ yxatidan iborat. Bitiruv malakaviy ishimda qo ‘ yilgan masala yuzasidan asosiy
va yordamchi adabiyotlar o ‘ rganildi. Shuningdek, bu soha algebraning yangi va
zamonaviy sohalaridan biri bo‘lganligi va bu yo ‘ nalishdagi dastlabki o ‘ zbek
tilidagi fundamental ma’lumotlar to ‘ planganligi bilan ahamiyatlidir.
3

I.BOB. UMUMIY TUSHUNCHALAR. MAYDON VA VEKTOR FAZO
TUSHUNCHALARI. ASSOSIATIV VA NOASSOSIATIV ALGEBRALAR.
1.1- §. GRUPPA, HALQA VA MAYDON
Bizga bo‘sh bo‘lmagan A to‘plam va A × A dekart ko‘paytma berilgan
bo‘lsin. A × A dekart ko‘paytmani A to‘plamga o‘tkazuvchi ∗ : A × A → A
asklantirish berilgan bo‘lsa, u holda A to‘plamda binar amal aniqlangan deyiladi
[2].
Ushbu (A, ∗ ) juftlikka esa algebraik sistema yoki gruppoid deb ataladi.
Odatda (a, b) elementning bu akslantirishdagi qiymati a ∗ b, a · b yoki ab kabi
belgilanadi.
1.1.1-misol.
• Bizga biror A to‘plam berilgan bo‘lib, ushbu to‘plamdan olingan ixtiyoriy
x va y elementlar uchun x ∗ y = x ko‘rinishda aniqlangan ∗ amali binar
amal bo‘ladi.
• N natural sonlar to‘plamida quyidagi amallar binar amal bo‘ladi: natural
sonlarni qo‘shish, ko‘paytirish, ikki sonning maksimumi, minimumi, eng
katta umumiy bo‘luvchisi va eng kichik umumiy karralisi.
• Z butun sonlar to ‘ plamida qo ‘ shish (+) va ko ‘ paytirish (·) amallari binar
amal bo’ladi.
• [a, b] kesmada uzluksiz bo‘lgan barcha funksiyalar fazosi C[a, b] da
ixtiyoriy f, g
∈ C [a, b] funksiyalar uchun (f ◦ g)(x) = f (g(x)) kabi
aniqlangan funksiyalar kompozitsiyasi (superpozitsiya) deb ataluvchi amal
binar amal bo‘ladi.
1.1.1-ta’rif . Agar (S,
∗ ) algebraik sistemada ixtiyoriy a, b, c ∈ S elementlar
uchun assosiativlik xossasi, ya’ni (a
∗ b) ∗ c = a ∗ (b ∗ c) tenglik o‘rinli bo‘lsa, u
holda (S,
∗ ) algebraik sistemaga yarim gruppa deyiladi.
1.1.2-misol .
• (N, +), (N, ·), (Z, ·) algebraik sistemalar yarim gruppa bo‘ladi.
• A to‘plamda olingan ixtiyoriy x, y elementlar uchun
∗ amali x ∗ y = x
5

ko‘rinishda aniqlangan bo‘lsa, (A, ∗ ) algebraik sistema yarim gruppa
bo‘ladi.
1.1.2-ta’rif. Agar (M,
∗ ) yarim gruppada shunday e ∈ M element mavjud
bo‘lib, ixtiyoriy a
∈ M element uchun e ∗ a = a ∗ e = a tenglik bajarilsa, u holda
(M,
∗ ) yarim gruppaga monoid deyiladi. Ushbu e element esa birlik element deb
ataladi.
1.1.3-misol.
• (Z, ·), (N, ·), (Z, +) algebraik sistemalar monoid tashkil qiladi.
• (M
n (R), +) – elementlari haqiqiy sonlardan iborat bo‘lgan n-tartibli
kvadrat matritsalar to‘plami, matritsalarni qo‘shish amaliga nisbatan
monoid tashkil qiladi.
• (M
n (R), ·) – elementlari haqiqiy sonlardan iborat bo‘lgan n-tartibli kvadrat
matritsalar to‘plami, matritsalarni ko‘paytirish amaliga nisbatan monoid
tashkil qiladi.
Endi asosiy tushuncha hisoblangan gruppaning ta’rifini keltiramiz .
1.1.3-ta’rif . Agar (G,
∗ ) monoid berilgan bo‘lib, ixtiyoriy a ∈ G element
uchun a −1
∗
a = a ∗ a −1
= e tenglikni qanoatlantiruvchi a −1 ∈
G element mavjud
bo‘lsa, u holda (G,
∗ ) algebraik sistemaga gruppa deyiladi. a −1
element esa a
elementning teskari elementi deb ataladi.
Demak, gruppa bu biror bo‘sh bo‘lmagan to‘plamda aniqlangan algebraik
amalga nisbatan assosiativlik xossasi o‘rinli bo‘ladigan, birlik elementi mavjud
bo‘lib, ixtiyoriy elementi teskarilanuvchi bo‘ladigan algebraik sistema ekan.
Agar (G, ∗ ) gruppaning ixtiyoriy a, b ∈ G elementlari uchun a ∗ b = b ∗ a
tenglik o‘rinli bo‘lsa, u holda (G, ∗ ) gruppa kommutativ gruppa yoki Abel
gruppasi deyiladi. Kommutativ bo‘lmagan gruppa esa nokommutativ gruppa
deyiladi.
1.1.4-misol.
• (Z, +), (Q, +), (R, +), (C, +) algebraik sistemalar kommutativ gruppa
bo‘ladi.
6

$• (Q \ {0}, ·), (R \ {0}, ·), (C \ {0}, ·) algebraik sistemalar kommutativ gruppa bo‘ladi. • (M n (R), +) – elementlari haqiqiy sonlardan iborat bo‘lgan n-tartibli kvadrat matritsalar to‘plami, matritsalarni qo‘shish amaliga nisbatan kommutativ gruppa tashkil qiladi. • (GL n (R), ·) – elementlari haqiqiy sonlardan iborat bo‘lib, determinanti noldan farqli bo‘lgan n-tartibli kvadrat matritsalar to‘plami, matritsalarni ko‘paytirish amaliga nisbatan nokommutativ gruppa tashkil qiladi. • (SL n (R), ·) – elementlari haqiqiy sonlardan iborat bo‘lib, determinanti 1 ga teng bo‘lgan n-tartibli kvadrat matritsalar to‘plami, matritsalarni ko‘paytirish amaliga nisbatan nokommutativ gruppa tashkil qiladi. Qiyudagi misolda bo‘sh bo‘lmagan X to‘plamning barcha qism to‘plamlaridan tuzilgan P (X ) oilani qarab, bu oila ikki to‘plamning birlashmasi, kesishmasi va simmetrik ayirmasi kabi amallarga nisbatan qanday algebraik sistema tashkil qilishini aniqlaymiz. 1.1.5-misol. Bo‘sh bo‘lmagan X to‘plamning barcha qism to‘plamlaridan tuzilgan P (X ) sistema uchun quyidagilar o‘rinli bo‘ladi: • P (X ) to‘plam birlashma ∪ amaliga nisbatan monoid tashkil qiladi, lekin (P (X ), ∪ ) gruppa emas. Haqiqatdan ham, birlashma amali binar amal bo‘lib, ushbu amal uchun assosiativlik xossasi o‘rinli bo‘ladi. Birlik element vazifasini e = ∅ bajarsa, bo‘sh to‘plamdan farqli bo‘lgan ixtiyoriy to‘plam teskarilanuvchi emas. Shuning uchun (P (X ), ∪ ) monoid bo‘lib, gruppa tashkil qilmaydi. • P (X ) to‘plam kesishma ∩ amaliga nisbatan monoid tashkil qiladi, lekin (P (X ), ∩) gruppa emas. Bu yerda ham aniqlangan amal binar amal bo‘lishi va assosiativlikning bajarilishi ravshan. Birlik element vazifasini e = X bajarsa, X dan farqli bo‘lgan ixtiyoriy to‘plam teskarilanuvchi emas. 7$ $• P (X ) to‘plam simmetrik ayirma ∆ amaliga nisbatan kommutativ gruppa tashkil qiladi. Chunki, simmetrik ayirmaga nisbatan birlik element e = ∅ bo‘lib, ixtiyoriy A ∈ P (X ) elementning teskarisi o‘ziga teng bo‘ladi, ya’ni A −1 = A. Bizga sonlar nazariyasidan ma’lumki, ixtiyoriy n natural son uchun Z n ={0, 1, . . . , n − 1} chegirmalar sinfini hosil qilish mumkin, hamda bu chegirmalar sinfida qo‘shish va ko‘paytirish amallari aniqlanadi. 1.1.6-misol . Z n = {0, 1, . . . , n − 1} chegirmalar sinfi uchun quyidagilar o‘rinli: • (Z n , + n ) kommutativ gruppa tashkil qiladi. Bu yerda birlik element vazifasini 0 element bajaradi, k elementning teskarisi n-k element bo’ladi. • (Z n , · n ) monoid tashkil qiladi, lekin gruppa bo‘lmaydi. Bu yerda assosiativlik o‘rinli, birlik element vazifasini 1 element bajaradi ammo barcha elementlari ham teskarilanuvchan emas (masalan 0 element). 1.1.7-misol. (Z n , · n ) monoidning barcha teskarilanuvchi elementlari to‘plami U n = {a ∈ Z n \ {0} | (a, n) = 1} ko‘rinishida bo‘lib, bu to‘plam ko‘paytirish amaliga nisbatan gruppa tashkil qiladi. Ya’ni (U n , · n ) kommutativ gruppa. Endi gruppaning ba’zi sodda xossalarini o‘z ichiga olgan qiyudagi tasdiqni keltiramiz. 1.1.1-tasdiq. Ixtiyoriy (G, ∗ ) gruppa uchunquyidagilar o ‘ rinli: 1) Gruppaning birlik elementi yagona. 2) Ixtiyoriy a∈G element uchun yagona teskari element mavjud. 3) Ixtiyoriy a∈G element uchun (a−1)−1=a tenglik o‘rinli. 4) Ixtiyoriy a , b ∈ G elementlar uchun ( a ∗ b ) − 1 = b − 1 ∗ a − 1 tenglik o‘rinli. Isbot. 1) Faraz qilaylik (G, ∗ ) gruppada ikkita e1 va e2 birlik elementlar mavjud bo‘lsin. U holda e1∗e2 ko‘paytmani qarasak, e1 element birlik element bo‘lganligi uchun e1∗e2=e2 . Ikkinchi tomondan esa, e2 element birlik element bo‘lganligi uchun e1∗e2=e1 . Demak, e 1 = e 2 . 2) Faraz qilaylik a∈G element uchun ikkita teskari element mavjud bo‘lsin, ya’ni shunday b , c ∈ G elementlar mavjud bo‘lib, a∗b= b∗a=e,a∗c= c∗a=e bo‘lsin. Quyidagi tengliklardan b va c elementlarning tengligini hosil qilamiz: 8$

b = b ∗ e = b ∗( a ∗ c ) = ( b ∗ a ) ∗ c = e ∗ c = c .
Demak,
a elementga teskari element yagona.
3)
a∈G elementning teskarisi
a − 1
bo‘lganligi uchun
a ∗ a − 1
= a − 1
∗ a = e .
Faraz qilaylik, b ∈ G
element
a−1 ga teskari element bo‘lsin. U holda
b∗a−1= a−1∗b=e.
Bu tengliklardan biz
a va b elementlar
a − 1
ga teskari element ekanligini hosil qil-
amiz. 2)-xossaga ko‘ra ixtiyoriy elementning teskari elementi yagona bo‘lganligi
uchun
b=a ekanligi kelib chiqadi. b element
a − 1
ning teskarisi ekanligidan
( a − 1
) − 1
= a bo‘ladi.
4) Bizga a , b ∈ G
elementlar berilgan bo‘lib,
a−1 va b−1 elementlar ularning
teskari elementlari bo‘lsin, ya’ni
a∗a−1= a−1∗a=e,b∗b−1= b−1∗b= e
Quyidagi tengliklarni qaraymiz
( a ∗ b ) ∗ ( b − 1
∗ a − 1
) =
( a ∗ ( b ∗ b − 1 )
∗ a − 1 )
= ( a ∗ e ) ∗ a − 1
= a ∗ a − 1
= e .
(b−1∗a−1)∗(a∗b)=(b−1∗(a−1∗a))∗b=(b−1∗e)∗b=b−1∗b= e.
Ushbu tengliklardan
a∗b elementning teskarisi
b − 1
∗ a − 1
ekanligi kelib chiqadi, ya’ni
( a ∗ b ) − 1
= b − 1
∗ a − 1
.
Yuqorida biz bitta binar amalga ega bo‘lgan algebraik sistemalarni, ya’ni
gruppalarni qaradik. Endi navbatda ikkita binar amal bilan aniqlanuvchi algebraik
sistema bo’lgan halqa tushunchasini qaraymiz. Gruppadagi ko‘plab
tushunchalarning analoglari halqalar uchun ham aniqlanishi bilan bir qatorda, faqat
halqalarga tegishli bo‘lgan tushunchalar ham mavjud.
Bizga bo‘sh bo‘lmagan R to‘plam berilgan bo‘lib, unda ikkita binar amal
aniqlangan bo‘lsin. Ushbu binar amallarni + va · kabi belgilab, ularni shartli
ravishda qo‘shish va ko‘paytirish amallari deb ataymiz [2].
1.1.4-ta’rif. Bo‘sh bo‘lmagan R to‘plamda aniqlangan + va · binar amallari
quyidagi shartlarni qanoatlantirsa:
1) (R, +) kommutativ gruppa;
2) (R, ·) yarim gruppa;
3) Barcha a, b, c
∈ R elementlar uchun
a · (b + c) = (a · b) + (a · c), (b + c) · a = (b · a) + (c · a) tengliklar o’rinli
bo’lsa, u holda (R, +, ·) uchlikka halqa deyiladi.
9

Boshqacha qilib aytganda, bo‘sh bo‘lmagan R to‘plamdagi + va · binar
amallari uchun quyidagi aksiomalar bajarilsa, u holda (R, +, ·) halqa deb ataladi:
(R
1 ) Ixtiyoriy a, b, c ∈ R elementlar uchun (a + b) + c = a + (b + c).
(R
2 ) Ixtiyoriy a, b ∈ R elementlar uchun a + b = b + a.
(R
3 ) Shunday 0 ∈ R element mavjudki, ixtiyoriy a ∈ R uchun a + 0 = a.
(R
4 ) Ixtiyoriy a ∈ R uchun shunday −a ∈ R element mavjudki, bunda
a + (−a) = 0.
(R
5 ) Ixtiyoriy a, b, c ∈ R elementlar uchun (a · b) · c = a · (b · c).
(R
6 ) Ixtiyoriy a, b, c ∈ R elementlar uchun a · (b + c) = (a · b) + (a · c) va
(b + c) · a = (b · a) + (c · a).
Halqadagi 0 elementni halqaning nol elementi deyiladi. Odatda halqalar
uchun a·b o‘rniga ab belgilashdan a+(−b) o‘rniga esa a−b belgilashdan foydalanish
qabul qilingan.
1.1.8-misol. Z butun sonlar to‘plami odatdagi qo‘shish va ko‘paytirish
amallariga nisbatan halqa bo‘ladi. Bundan tashqari, ratsional sonlar to‘plami Q,
haqiqiy sonlar to‘plami R va kompleks sonlar to‘plami C ham qo‘shish va
ko‘paytirish amallariga nisbatan halqa tashkil qiladi.
1.1.5-ta’rif. R halqaning barcha a, b ∈ R elementlari uchun ab = ba tenglik
o‘rinli bo‘lsa, u holda R halqa kommutativ halqa deyiladi. Kommutativ bo‘lmagan
halqalarga esa nokommutativ halqa deb ataladi.
Agar
R halqada ko‘paytirish amaliga nisbatan birlik element mavjud bo‘lsa,
ya’ni shunday e ∈ R
element topilib, ixtiyoriy a ∈ R
uchun ea = ae = a
tenglik o‘rinli
bo‘lsa, u holda ushbu
e elementga halqaning birlik elementi deyiladi.
Gruppalar nazariyasidan ma’lumki, ixtiyoriy algebraik sistemaning birlik
elementi yagona bo‘ladi. Demak, halqaning birlik elementi ham yagona bo‘lib, biz
uni 1 orqali belgilaymiz. Birlik elementga ega bo‘lgan halqa biri bor halqa deb
ataladi.
1.1.9-misol . (Z, +, ·), (Q, +, ·) (R, +, ·) va (C, +, ·) halqalar biri bor
kommutativ halqalarga misol bo‘ladi.
10

1.1.10-misol . (2Z, +, ·) juft sonlar to‘plami birlik elementga ega bo‘lmagan
halqa bo‘ladi.
1.1.11-misol . Agar R kommutativ halqa bo‘lsa, u holda R ustida aniqlangan
bir o‘zgaruvchili ko‘phadlar to‘plami R[x], ko‘phadlarni qo‘shish va ko‘paytirish
amallari bilan birgalikda kommutativ halqa bo‘ladi. Xususan, (Z[x], +, ·), (Q[x],
+, ·), (R[x], +, ·) va (C[x], +, ·) halqalar kommutativ bo‘ladi.
1.1.12-misol . Chegirmalar sinfi Z
n = {0, 1, . . . , n-1} to‘plam unda
aniqlangan
qo‘shish va ko‘paytirish amallari bilan birgalikda halqa tashkil qiladi. (Z
n , +
n , ·
n )
halqa chegirmalar halqasi deb ataladi.
Yuqorida biz faqat kommutativ halqalarga misollar keltirdik. Quyidagi
misolda esa nokommutativ halqaga misol keltiramiz.
1.1.13-misol . Elementlari biror R halqadan olingan n-tartibli kvadrat
matritsalar to‘plami M
n (R) matritsalarni qo‘shish va ko‘paytirish amallariga
nisbatan halqa tashkil qiladi. Matritsalarni ko‘paytirish amali uchun
kommutativlik o‘rinli bo‘lmaganligi sababli (M
n (R), +, ·) nokommutativ halqa
bo‘ladi.
Yuqoridagi misoldan ko‘rinadiki, M
n (Z), M
n (Q), M
n (R) va M
n (C) halqalar,
ya’ni elementlari mos ravishda butun, ratsional, haqiqiy va kompleks sonlardan
iborat bo‘lgan n-tartibli kvadrat matritsalar to‘plamlari nokommutativ halqalar
bo‘ladi. Ushbu matritsalar to‘plamlarida birlik matritsa yotganligini hisobga olsak,
ular birlik elementga ega bo‘lgan halqalar bo‘ladi. M
n (2Z) to‘plam, ya’ni
elementlari juft sonlardan iborat matritsalar to‘plami esa birlik elementga ega
bo‘lmagan nokommutativ halqa bo‘ladi. Endi halqaning ayrim elementar
xossalarini keltiramiz.
1.1.1-teorema . R halqa va ixtiyoriy a, b ∈ R elementlar uchun quyidagi
tengliklar o‘rinli:
1) a0 = 0a = 0.
2) a(−b) = (−a)b = −(ab).
11

Isbot. 1) aa + a0 = a(a + 0) = aa tenglikdan a0 elementning qo‘shishga nisbatan
neytral element ekanligi kelib chiqadi, demak, a0 = 0. Xuddi shunga o‘xshab 0a =
0 tenglikni hosil qilish mumkin.
2) 0 = a(b − b) = ab + a(−b) tenglikdan a(−b) = −(ab) ekanligi kelib chiqadi.
Xuddi shunga o‘xshab (−a)b = −(ab) tenglik ham osongina ko‘rsatiladi.
Ta’kidlash joizki, agar R biri bor halqa bo‘lib, R ≠
{0} bo‘lsa, u holda uning 0
va 1 elementlari har xil bo‘ladi. Haqiqatdan ham, agar 1 = 0 bo‘lsa, u holda
ixtiyoriy a ∈ R element uchun a = a1 = a0 = 0. Bu esa R ≠
{0} ekanligiga zid.
Aytaylik, R biri bor halqa bo‘lsin. Agar u ∈ R element uchun shunday v ∈ R
element topilib, uv = vu = 1 shart bajarilsa, u holda u element teskarilanuvchi
deyiladi, v element esa u elementning teskarisi deb ataladi va u -1
kabi belgilanadi.
1.1.2-teorema. R biri bor halqaning barcha teskarilanuvchi elementlaridan
tuzilgan T to‘plam uchun quyidagilar o‘rinli:
1) T ≠
∅
2) 0 T
3)
∀ a, b ∈ T uchun ab ∈ T .
Isbot. 1) 1 · 1 = 1 = 1 · 1 bo‘lganligi uchun 1 ∈ T , demak T
≠ ∅ .
2) Ixtiyoriy v ∈ R element uchun 0 v = 0 ekanligi va 0 ≠
1 bo‘lganligi uchun
0 T bo‘ladi.
3) Aytaylik, a, b ∈ T bo‘lsin, u holda c, d ∈ R elementlar topilib, ac = ca = 1
va bd = db = 1. Ushbu
(ab)(dc) = a(bd)c = ac = 1,
(dc)(ab) = d(ca)b = db = 1
tengliklardan esa
ab elementning teskarilanuvchi ekanligi kelib chiqadi, ya’ni ab ∈ T
.
Yuqoridagi teoremadan kelib chiqadiki, biri bor halqaning barcha
teskarilanuvchi elementlaridan tashkil topgan to‘plam ko‘paytirish amaliga
nisbatan gruppa tashkil qiladi.
12

$1.1.6 -ta’rif. Agar biri bor halqaning ixtiyoriy noldan farqli elementi teskarilanuvchi bo‘lsa, u holda u jism deyiladi. Kommutativ jismga maydon deb ataladi. Ta’kidlash joizki, (R, +, ·) halqa jism bo‘lishi uchun (R \ {0}, ·) algebraik sistemaning gruppa bo‘lishi zarur va yetarli. O‘z navbatida R halqa maydon bo‘lishi uchun esa (R \ {0}, ·) algebraik sistemaning kommutativ gruppa bo‘lishi zarur va yetarli. 1.1.14 -misol . 1) Butun sonlar halqasi (Z, +, ·) maydon tashkil qilmaydi, chunki uning 1 va -1 dan boshqa elementlari teskarilanuvchi emas. 2) Ratsional, haqiqiy va kompleks sonlar to‘plami (Q, +, ·), (R, +, ·), (C, +, ·) maydon bo‘ladi. Endi halqalarda yana bir muhim tushuncha bo‘lgan nolning bo‘luvchisi tushunchasini kiritamiz. 1.1.7 -ta’rif. Halqaning noldan farqli a ∈ R elementi uchun, shunday noldan farqli b∈ R element topilib, ab =0 yoki ba =0 bo‘lsa, u holda a element nolning bo‘luvchisi deb ataladi. Ta’kidlash joizki, jismda xususan maydonda, nolning bo‘luvchisi mavjud emas. Chunki, ab = 0 bo‘lsa, u holda b = (a −1 a)b = a −1 (ab) = a −1 0 = 0 tenglikdan b = 0 ekanligi kelib chiqadi. 1.1.8-ta’rif . Nolning bo‘luvchisiga ega bo‘lmagan kommutativ biri bor halqaga butunlik sohasi deyiladi. 1.1.15-misol. Butun sonlar halqasi (Z, +, ·) butunlik sohasi bo‘ladi. Juft sonlar to‘plami (2Z, +, ·) esa birlik elementga ega bo‘lmagan kommutativ halqa bo‘lib, nolning bo‘luvchilari mavjud emas. 1.1.16-misol. Matritsalar halqasi (M 2 (R), +, ·) nokommutativ halqa bo ‘ lish bilan birgalikda, nolning bo‘luvchilariga ega. Xususan, ( 0 0 0 1 ) va ( 0 1 0 0 ) matritsalar nolning bo‘luvchilari bo‘ladi, chunki 13$

(
0 0
0 1)∗(
0 1
0 0)=(
0 0
0 0)Quyidagi teoremada nolning bo‘luvchilari bilan halqadagi qisqartirish
qoidasi
orasidagi bog‘lanishni keltiramiz.
1.1.3-teorema. Nolning bo ‘ luvchisiga ega bo ‘ lmagan halqada qisqartirish
qoidasi o ‘ rinli, ya’ni a , b , c ∈ R
, a ≠ 0
elementlar uchu ab = ac
n ekanligidan
b=c kelib
chiqadi (
ba =ca ekanligidan b=c kelib chiqadi). Bu qisqartirish qoidalari mos
ravishda chap va o’ng qisqartirish qoidalari deb ataladi. Va aksincha, agar
qisqartirish qoidalaridan (chap yoki o’ng) biri o’rinli bo ‘ lsa, u holda R nolning
bo ‘ luvchisiga ega emas.
Isbot. Faraz qilaylik, R nolning bo`luvchisiga ega bo`lmasin. Aytaylik,
a , b , c ∈ R
elementlar uchun ab = ac
bo‘lib a ≠ 0
, bo‘lsin. U holda ab − ac = 0
ekanligidan a
( b − c ) = 0
kelib chiqadi. R nolning bo‘luvchisiga ega bo‘lmaganligi va
a ≠ 0
ekanligidan
b−c= 0 , ya’ni b = c
kelib chiqadi. Xuddi shunga o‘xshab, ba − ca = 0

ekanligidan ham
b=c tenglikni keltirib chiqarish mumkin.
Va aksincha, R halqada qisqartirish qoidalaridan biri aytaylik, chap qisqar-
tirish qoidasi o‘rinli bo‘lsin. Teskarisini faraz qilaylik, ya’ni R halqa nolning
bo‘luvchisiga ega bo‘lsin. Aytaylik, a ∈ R
element nolning bo‘luvchisi bo‘lsin,
ya’ni
b≠0 element topilib ab =0 . U holda ab = a0 ekanligidan va chap qisqar-
tirish qoidasi o‘rinliligidan b = 0
kelib chiqadi. Bu esa, a nolning bo‘luvchisi
ekanligiga zid. Demak, R nolning bo‘luvchisiga ega emas.
1.1.9-ta’rif. Elementlari soni chekli bo’lgan halqa chekli halqa, aks holda
cheksiz halqa deyiladi.
Chegirmalar halqasi ¿ ¿
chekli halqa bo’lsa, (Z, +, ·
), (Q, +, ·
), ( R , + , · )
va ¿ ¿
)
halqalar cheksiz halqalar bo ‘ ladi. Bundan tashqari
¿¿ halqa n murakkab son
bo’lgan holda nolning bo’luvchisiga ega bo ‘ lgan halqa bo’ladi. Masalan ¿ ¿
halqada
2·3= 0
, ya’ni 2 va 3 nolning bo ‘ luvchilari.
1.2- §. VEKTOR FAZO VA UNGA MISOLLAR
14

Bizga V to‘plam berilgan bo‘lsin. Ixtiyoriy x, y ∈ V elementlarga ularning
yig‘indisi deb ataluvchi z ∈ V elementni mos qo‘yib, uni z := x + y ko‘rinishda
belgilab olamiz. Shuningdek, biror K (R yoki C) maydondan olingan ixtiyoriy λ ∈
K sonini x ∈ V elementga ko‘paytmasi sifatida y ∈ V elementni mos qo‘yamiz va
uni y := λ · x ko‘rinishda belgilaymiz [3].
1.2.1-ta’rif . Agar V to‘plamda aniqlangan qo‘shish va songa ko‘paytirish
amallari quyidagi shartlarni qanoatlantirsa, V to‘plam chiziqli fazo yoki vektor
fazo deyiladi:
1) x + y = y + x (kommutativlik sharti);
2) (x + y) + z = x + (y + z ) (assosiativlik sharti);
3) shunday 0 ∈ V element mavjud bo‘lib, har qanday x ∈ V uchun x + 0 =
0 + x = x, bu yerdagi 0 element nol element deyiladi;
4) har qanday x
∈ V uchun −x ∈ V bilan belgilanadigan shunday
element mavjud bo‘lib, x + (−x) = (−x) + x = 0;
5) 1 · x = x;
6) α · ( β · x) = αβ · x = β · ( α · x);
7) (α + β ) · x = α · x + β · x;
8) α · (x + y) = α · x + α · y ;
bu yerda α, β, 1
∈ K, x, y, z ∈ V.
1.2.1-misol .
a) Haqiqiy (kompleks) sonlar maydoni R (C) o‘z ustida chiziqli fazo tashkil
etadi.
b) Tekislikdagi (fazodagi) vektorlar to‘plami vektorlarni qo‘shish va songa
ko‘paytirish amallariga nisbatan chiziqli fazo tashkil etadi.
c) Darajasi n dan oshmaydigan haqiqiy (kompleks) koeffitsientli barcha
ko‘phadlar to‘plami ko‘phadlarni qo‘shish va ko‘phadni songa ko‘paytirish
amallariga nisbatan chiziqli fazo tashkil etadi.
d) Barcha n × m-tartibli matritsalar to‘plami matritsalarni qo‘shish va
matritsani songa ko‘paytirish amallariga nisbatan chiziqli fazo tashkil etadi.
15

Chiziqli fazo elementlarini vektorlar deb atash qabul qilingan. Agar chiziqli
fazo haqiqiy (kompleks) sonlar maydonida berilgan bo‘lsa, haqiqiy (kompleks)
chiziqli fazo deyiladi.
Bizga V chiziqli fazo berilgan bo‘lib, x
1 , x
2 , . . . , x
n vektorlar chiziqli
fazoning elementlari bo‘lsin. Ushbu α
1 x
1 + α
2 x
2 + . . . + α
n x
n yig‘indi vektorlarning
chiziqli kombinatsiyasi deyiladi, bu yerda α
i ∈ K.
1.2.2-ta’rif. Agar kamida bittasi noldan farqli bo‘lgan α
1 , α
2 , . . . , α
n sonlar
mavjud bo‘lib,α1x1 + α
2 x
2 + . . . + α
n x
n = 0 tenglik o‘rinli bo‘lsa, u holda x
1 , x
2 , . . .
, x
n vektorlar chiziqli bog‘liq vektorlar deyiladi. hiziqli bog‘liq bo‘lmagan
vektorlar chiziqli erkli vektorlar deyiladi. Ya’ni, α
1 x
1 + α
2 x
2 + . . . + α
n x
n = 0
tenglik α
1 = α
2 = . . . = α
n = 0 bo‘lgan holdagina o‘rinli bo‘lsa, x
1 , x
2 , . . . , x
n
vektorlar chiziqli erkli vektorlar deyiladi.
1.1.1-tasdiq. Agar x
1 , x
2 , . . . , x
n vektorlar chiziqli bog‘liq bo‘lsa, u holda
ulardan kamida bittasi qolganlarining chiziqli kombinatsiyasi orqali ifodalaniladi.
va aksincha, agar vektorlarning bittasi qolganlarining chiziqli kombinatsiyasi
orqali ifodalansa, bu vektorlar chiziqli bog‘liq bo‘ladi.
Isbot. Aytaylik, x
1 , x
2 , . . . , x
n vektorlar chiziqli bog‘liq bo‘lsin. U holda
α
1 x
1 + α
2 x
2 + . . . + α
n x
n = 0
chiziqli kombinatsiyadagi koeffitsientlarning kamida bittasi noldan farqli.
Umumiylikka ziyon yetkazmagan holda α
1 ≠
0 deb olish mumkin. U holda
α
1 x
1 = −α
2 x
2 − α
3 x
3 − . . . − α
n x
n
tenglikdan x1= −a2
a1
x2− a3
a1
x3−...− an
a1
xn
kelib chiqadi. λ
1 = − a
i
a
1 x
2 , 2 ≤ i ≤ n kabi belgilasak, x
1 vektor x
2 , x
3 , . . . , x
n
vektorlarning chiziqli kombinatsiyasi shaklida
x
1 = λ
2 x
2 + λ
3 x
3 + . . . + λ
n x
n
kabi ifodalanishini hosil qilamiz. Aksincha, agar x
1 vektor x
2 , x
3 , . . . , x
n
vektorlarning chiziqli kombinatsiyasi shaklida
16

x
1 = λ
2 x
2 + λ
3 x
3 + . . . + λ
n x
n
kabi ifodalansa, x
1 − λ
2 x
2 − λ
3 x
3 − . . . – λ
n x
n = 0 tenglikdan x
1 , x
2 , . . . , x
n
vektorlarning chiziqli bog‘liq ekanligi kelib chiqadi.
1.2.2-misol. Agar x
1 , x
2 , . . . , x
n vektorlar orasida nol vektor bo‘lsa, u holda
bu vektorlar chiziqli bog‘liq bo‘ladi.
Endi fazoning o‘lchami tushunchasini kiritamiz .
1.2.3-ta’rif. Agar V chiziqli fazoda n ta chiziqli erkli vektor mavjud bo‘lib,
bundan ortiq sondagi chiziqli erkli vektorlar mavjud bo‘lmasa, u holda V chiziqli
fazo n o‘lchamli fazo deyiladi. Chiziqli fazoning o‘lchami dim(V ) kabi belgilanadi .
Agar V fazoda cheksiz ko‘p chiziqli erkli vektorlar mavjud bo‘lsa, u holda V
fazo cheksiz o‘lchamli fazo deyiladi.
1.2.4-ta’rif. n o‘lchamli V fazodagi n ta chiziqli erkli e
1 , e
2 , . . . , e
n vektorlar
V fazoning bazisi deb ataladi.
1.2.3-misol.
a) To‘g‘ri chiziqdagi vektorlar to‘plamida har qanday ikki vektor
proporsional, ya’ni chiziqli bog‘liqdir. Demak, to‘g‘ri chiziq bir o‘lchamli fazoga
misol bo‘ladi.
b) Tekislikda ikkita chiziqli erkli vektor mavjud, ammo har qanday uchta
vektor chiziqli bog‘liq bo‘ladi. Bundan esa, tekislik ikki o‘lchamli chiziqli fazo
ekanligi kelib chiqadi.
Bizga n o‘lchamli V chiziqli fazo va uning biror bazisi berilgan bo‘lsin.
1.2.1-teorema. n o‘lchamli V chiziqli fazoning ixtiyoriy elementini bazis
vektorlarning chiziqli kombinatsiyasi orqali yagona ravishda ifodalash mumkin.
Isbot. Bizga x ∈ V element va e
1 , e
2 , . . . , e
n bazis berilgan bo‘lsin. Chiziqli
fazo n o‘lchamli bo‘lganligi uchun n + 1 ta vektordan iborat x, e
1 , e
2 , . . . , e
n
vektorlar chiziqli bo‘g‘liq bo‘ladi. Demak, kamida bittasi noldan farqli bo‘lgan α
0 ,
α
1 , α
2 , . . . , α
n sonlar topilib, α
0 x + α
1 e
1 + α
2 e
2 + . . . + α
n e
n = 0 tenglik bajariladi.
Agar α
0 = 0 bo‘lsa, u holda α
1 e
1 + α
2 e
2 + . . . + α
n e
n = 0 tenglikdan va e
1 , e
2 , . . . , e
n
vektorlarning chiziqli erkli ekanligidan α
1 = α
2 =. . . = α
n = 0 ekanligi kelib chiqadi.
Bu esa yuqoridagi mulohazaga zid.
17

Demak, α
0≠ 0 bo‘lib,
x1= −a1
a0
e1− a2
a0
e2−...− an
a0
en
ekanligi kelib chiqadi, ya’ni x ∈ V vektor e
1 , e
2 , . . . , e
n vektorlarning chiziqli
kombinatsiyasi orqali ifodalanadi.
Endi hosil qilingan ifodaning yagona ekanligini ko‘rsatamiz. Faraz qilaylik,
x vektorning bazis vektorlar orqali ikki xil ifodasi mavjud bo‘lsin, ya’ni:
x = ξ
1 e
1 + ξ
2 e
2 + . . . + ξ
n e
n va x = η
1 e
1 + η
2 e
2 + . . . + η
n e
n .
Bu ifodalarni tenglab,
(ξ
1 − η
1 )e
1 + (ξ
2 − η
2 )e
2 + . . . + (ξ
n − η
n )e
n = 0 tenglikni hosil qilamiz. e
1 , e
2 , . . . , e
n
vektorlar chiziqli erkli bo‘lgani uchun, bu tenglik ξ
1 = η
1 ,ξ
2 = η
2 , . . . , ξ
n = η
n
bo‘lgandagina o‘rinlidir.
1.2.5-ta’rif. Agar e
1 , e
2 , . . . , e
n vektorlar n o‘lchamli fazoning bazisi bo‘lib,x
= ξ
1 e
1 + ξ
2 e
2 + . . . + ξ
n e
n bo‘lsa, u holda ξ
1 , ξ
2 , . . . , ξ
n sonlar x vektorning e
1 ,
e
2 , . . . , e
n bazisdagi koordinatalari deb ataladi.
6.1.1-teoremaga muvofiq, ma’lum e
1 , e
2 , . . . , e
n bazisda har bir vektor bir
qiymatli aniqlanadigan koordinatalarga ega. Aytaylik, x va y vektor e
1 , e
2 , . . . , e
n
bazisda mos ravishda ξ
1 , ξ
2 , . . . , ξ
n va ν
1 , ν
2 , . . . , ν
n koordinatalarga ega bo‘lsin,
ya’ni
x = ξ
1 e
1 + ξ
2 e
2 + . . . + ξ
n e
n , y = ν
1 e
1 + ν
2 e
2 + . . . + ν
n e
n .
U holda x + y vektor ξ
1 + ν
1 , ξ
2 + ν
2 , . . . , ξ
n + ν
n koordinatalarga ega bo‘ladi,
ya’ni x + y = (ξ
1 + ν
1 )e
1 + (ξ
2 + ν
2 )e
2 + . . . + (ξ
n + ν
n )e
n .
Shunday qilib, x
va
y vektorlarni qo‘shishda ularning bir xil bazisdagi
koordinatalari yig‘indisi olinadi.
Berilgan x
vektorni λ soniga ko‘paytirishda esa uning har bir koordinatasi
shu songa ko‘paytiriladi.
1.3- §. ALGEBRA TUSHUNCHASI. ASSOSIATIV VA NOASSASIATIV
ALGEBRALAR
18

Biz yuqoridagi paragraflarda gruppa, halqa, maydon va vektor fazolarga doir
asosiy ta’riflar, tushunchalar va ularga doir misollarni qaradik. Ularning ba’zi
muhim xossalarini keltirdik. Bu paragrafda biz algebra tushunchasiga, assosiativ
va noassosiativ algebralar tushunchalariga to‘xtalamiz, shuningdek bu
algebralarning ma’lum bo‘lgan va yaxshi o‘rganilgan ayrim turlarini, ularga
taalluqli bo‘lgan muhim tushunchalar va ta’riflarni keltiramiz [26].
1.3.1-ta’rif: F maydon ustida aniqlangan A vektor fazoda A× A to’plamdan A
ga akslantiruvchi bichiziqli ko‘paytma ( x , y ) → xy
aniqlangan, hamda bu
ko‘paytma ixtiyoriy
a,b∈F va barcha x,y,z∈A lar uchun quyidagi distributivlik
qonunlari deb ataluvchi tengliklarni qanoatlantirsa:
(ax +by )z=a(xz )+b(yz ),x(ay +bz )=a(xy )+b(xz ),
A
vektor fazoga algebra deyiladi.
A
algebraning o‘lchami deganda biz vektor fazoning o‘lchamini tushunamiz.
Agar
A vektor fazo chekli o‘lchamli vektor fazo bo‘lsa, A algebra ham chekli
o‘lchamli hisoblanadi.
F maydon ustida aniqlangan chekli o‘lchamli A
algebra
{e1,e2,… ,en} bazislar
bilan berilgan bo‘lsin. A
algebraning struktura o‘zgarmaslari F maydondan olingan
skalyarlar bo‘lib, c
ijk
∈ F ( i , j , k = 1 , … , n )
ular quyidagicha aniqlanadi:
e
i e
j =
∑
k = 1n
c
ⅈ jk
e
k .
Demak
A algebrada ko ‘ paytmani aniqlash - bu bazislar orasidagi ko ’ paytmani
aniqlashdir .
1.3.2-ta’rif: Elementlari c
ijk
∈ F ( i , j , k = 1 , … , n )
lardan iborat M = ( c
ijk
)
kubik
matritsaga (uch o‘lchamli)
A algebraning struktura o‘zgarmaslari matritsasi
deyiladi.
1.3.3-ta’rif:
A algebrada shunday 1∈A element topilib, barcha x∈A lar
uchun ushbu tengliklarni qanoatlantirsa
1·x= x·1= x,
u holda A
algebra birlik elementga ega algebra deyiladi.
1.3.4-ta’rif:
A algebraning involyutsiyasi bu barcha x,y∈A lar uchun
19

j(j(x))= xva j(xy )= j(y)j(x)shartlarni qanoatlantiruvchi chiziqli
j:A→ A akslantirishdir.
1.3.5-ta’rif: Barcha x , y ∈ A
lar uchun, x ≠ 0
bo’lganda , ushbu
x · v = y va w · x = y
tenglamalar A
da yechiluvchan bo’lsa, u holda A
algebra bo‘linishli algebra
deyiladi.
Algebradagi assotsiator bu,
( x , y , z ) = ( x · y ) · z − x · ( y · z )
shartni qanoatlantiruvchi uch chiziqli funktsiyadir.
1.3.6-ta’rif: Agar A
algebraning ixtiyoriy
x,y,z elementlari uchun
x·(y·z)=(x·y)·z
assosiativlik sharti bajarilsa, u holda algebra assosiativ algebra deyiladi.
Assosiativ algebra ta’rifini assosiator orqali keltirish ham mumkin, bu holda
assosiativlik sharti, barcha x , y , z ∈ A
lar uchun
(x,y,z)=0
shart bilan almashadi.
O‘z navbatida yuqoridagi assosiativlik sharti yetarlicha bajarilmasa, u holda
algebra noassosiativ algebra deyiladi.
1.3.7-ta’rif: A
algebraning ixtiyoriy x , y
elementlari uchun quyidagi o‘ng va
chap alternativ ayniyatlar o‘rinli bo‘lsa
(
y , x , x ) = 0 va ( x , x , y ) = 0 ,
A
algebra alternativ algebra deyiladi.
1.3.8-ta’rif:
A algebraning ixtiyoriy x elementi uchun
x 2
= 0 shart bajarilsa, A
algebra antikommutativ algebra deyiladi.
Aslida
x 2
= 0 shartdan
xy =− yx shart kelib chiqadi, haqiqatan x,y∈A bo‘lsa, u
holda x − y ∈ A
bo’ladi va ( x − y ) 2
= 0
tenglik o’rinli.
(
x − y ) ·( x − y ) = 0 ,
xx − xy − yx + yy = 0
oxirgi tenglikdan xy = − yx
tenglikni hosil qilamiz. Teskarisi maydon
xarakteristikasi 2 dan farqli bo‘lganda o‘rinli bo‘ladi.
Antikommutativ algebrada Yakobian tushunchasi quyidagicha aniqlanadi
20

J(x,y,z)=(xy )z+(yz )x+(zx )y1.3.9-ta’rif: Antikommutativ
A algebraning barcha x,y,z∈A lar uchun ushbu
J ( x , y , z ) = 0
Yakobi ayniyati o‘rinli bo‘lsa, u holda bu algebra Li algebrasi deyiladi.
1.3.10-ta’rif: Antikommutativ
A algebraning barcha x,y,z∈A lar uchun
ushbu
J ( x , y , xz ) = J ( x , y , z ) x
ayniyati o‘rinli bo‘lsa, u holda bu algebra Malsev algebrasi deyiladi.
Algebrada kommutator tushunchasi
[x,y]= xy − yx
ko’rinishidagi bichiziqli funksiya bilan aniqlanadi.
A
algebraning A−¿¿ minus algebrasi A kabi aniqlangan vektor fazo bo’lib,
faqat unda ko‘paytma vazifasini
[x,y] kommutator bajaradi.
1.3.11-ta’rif: Agar
A algebraning ixtiyoriy x,y elementlari uchun
x·y= y·x
kommutativlik sharti bajarilsa, u holda algebra kommutativ algebra deyiladi
1.3.12-ta’rif: Kommutativ A
algebraning ixtiyoriy x , y ∈ A
lar uchun ushbu
(x2,y,x)=0
Jordan ayniyati o‘rinli bo‘lsa, u holda bu algebra Jordan algebrasi deyiladi.
Algebrada Jordan ko ‘paytmasi (yoki antikommutator) tushunchasi
x∗y= xy − yx
ko’rinishidagi bichiziqli funksiya bilan aniqlanadi.
Xarakteristikasi 2 dan farqli bo‘lgan
F maydonda aniqlangan A algebraning
A+¿¿
pilus algebrasi A kabi aniqlangan vektor fazo bo‘lib, faqat unda ko‘paytma
x · y = 1
2 ( x ∗ y )
kabi aniqlanadi.
A
algebra va uning ikkita B,C ⊆ A qism to’plamlari berilgan bo‘lsin. BC
orqali yz , y ∈ B , z ∈ C
ko ‘paytmalar orqali hosil qilingan qism fazoni belgilaymiz.
A
algebraning B qism algebrasi deganda BB ⊆ B shartni qanoatlantiruvchi qism
fazoni tushunamiz.
21

S⊆ A to’plam orqali hosil qilingan qism algebra deganda S ni o’z ichiga
oluvchi A
algebraning eng kichik qism algebrasini tushunamiz.

A algebraning ideali (ikki tomonlama) bu
AB +BA ⊆ B
shartni qanoatlantiruvchi
B qism algebrasidir.
II.BOB. GENETIK VA EVOLYUTSION ALGEBRALAR
2.1- §. GENETIK VA EVOLYUTSION ALGEBRALAR TARIXI
Tarixda matematiklar va genetiklar bir vaqtlar Mendel genetikasini o‘rganish
uchun assotsiativ bo‘lmagan algebralardan foydalanganlar. Mendel birinchi bo‘lib
o‘zining genetik qonunlarini ifodalash uchun algebraik jihatdan juda mos bo‘lgan
belgilardan foydalangan [25]. Darhaqiqat, u keyinchalik bir qancha boshqa
mualliflar tomonidan “Mendel algebralari” deb atalgan. 1920-1930-yillarda
umumiy genetik algebralar tushunchasi kiritildi va bu yo‘nalish ko‘plab olimlarda
qiziqish uyg’otdi. Birinchilardan bo‘lib, Serebrovskiy jinsiy ko‘payishni
ko‘rsatadigan “
× ” belgisining algebraik talqinini bergan va Mendel qonunlarini
matematik formulada ifoda etgan [37]. Glivenkov bir yoki ikkita bog‘lanmagan
lokusu bo‘lgan diploid populyatsiyalar uchun Mendel algebralarini kiritdi [16].
Mustaqil ravishda Kostitzin ham Mendel qonunlarini ifodalash uchun “ramziy
ko‘paytirish” belgisini kiritdi [24]. Genetikada uchraydigan algebralarni tizimli
o’rganishni I.M.H.Etheringtonning ishlarida kuzatish mumkin [12]. U o‘zining bir
qator maqolalarida Mendel qonunlarining assosiativ bo‘lmagan algebralar nuqtai
nazaridan aniq matematik formulasini berishga muvaffaq bo‘ldi [11].
Etheringtondan tashqari, Gonshor [ 13 ], Schafer [39], Holgate [17,18], Hench [19],
Reiser [32], Abraham [1], Lyubich [23] va Worz-Busekoslar [ 41 ] bu soha rivojiga
22

fundamental hissa qo ‘ shgan. Sohada nashr etilmagan ikkita asarni alohida
ta ‘ kidlash joiz, garchi ular kitob shaklida chop etilmagan bo‘lsada, bu sohaning
keying rivojining davom etishida ahamiyatli bo‘lgan. Ulardan biri fan nomzodi,
zamonaviy axborot nazariyasi asoschisi Claude Shennonning 1940 yilda taqdim
etilgan Ph.D dissertatsiyasi hisoblanadi (Massachusets texnologiya instituti) [ 38 ].
Shennon ixtiyoriy chastotalardan boshlab populyatsiyaning kelajak avlodlarida
genetik tarkibni bashorat qilish uchun algebraik usulni ishlab chiqdi. Ikkinchisi
Charles Cottermanning Ph.D dissertatsiya ishi bo‘lib, u ham 1940 yilda taqdim
etilgan (Ogayo shtati universiteti) [6, 9]. Kotterman xuddi Shennon singari
sistematik tizimni ishlab chiqdi. U, shuningdek, hozirda “nasl bo‘yicha bir xil” deb
ataladigan hosila genlar kontseptsiyasini ilgari surdi.
Ushbu sohaning dastlabki kunlarida umumiy genetik algebralar yoki keng
aniqlangan genetik algebralar mustaqil, ko‘plab olimlarda qiziqish uyg‘otadigan
matematik sohaga aylanishi mumkinligi ko‘rindi, chunki bu algebralar umuman
assotsiativ emas va Li algebralari, alternativ algebralar yoki Jordan algebralari
kabi assotsiativ bo‘lmagan algebralarning ma’lum sinflariga tegishli emas edi.
Ularda juda ko‘p qiziqarli narsalarga olib keladigan o‘ziga xos xususiyatlarga
ega matematik natijalar mujassamlashgan edi. Masalan, berilgan maydonda
notrivial ko‘rinishga ega bo‘lgan barik algebralar, ularning darajali tenglamalar
koeffitsientlari faqat ushbu tasvirlar ostidagi tasvirlarning funktsiyalari bo‘lib, ular
matematiklar uchun yangi tushunchalar hisoblangan. 1980-yillarga qadar bu
sohada eng keng qamrovli asar bu Worz-Busekrosning kitobi hisoblangan [41].
So‘nggi natijalar, masalan genetik algebralarda genetik evolyutsiya haqida olingan
natijalarni Yu.I.Lyubichning kitobida topish mumkin [23]. Bu yo’nalishdagi yana
bir yaxshi maqola bu Reedning maqolasi hisoblanadi [35].
Umumiy genetik algebralar biologiya va matematika o‘rtasidagi o‘zaro
ta’sirning mahsulidir. Mendel genetikasi matematikaga “Umumiy genetik
algebralar” deb nomlanuvchi yangi yo‘nalishni kiritdi. Ushbu algebralarni
o‘rganish Mendel genetikasining algebraik strukturalarini (tuzilishini) ochib berdi,
23

bu genetik va evolyutsion hodisalarni tushunish yo‘lini soddalashtirdi va
qisqartirdi. Darhaqiqat, sof matematik tuzilmalar va tegishli genetik xususiyatlar
o‘rtasidagi o‘zaro bog‘liqlik bu sohani juda qiziqarli qiladi. Biroq, Baur [4] va
Korrens [11] birinchi marta xloroplast merosi Mendel qoidalaridan chetga
chiqqanligini aniqlagandan so‘ng va ancha keyinroq mitoxondrial gen irsiyati ham
xuddi shu tarzda aniqlandi va organella genlarining nomendel irsiyati ikkita
xususiyat bilan tanildi - ota-onadan meros va vegetativ segregatsiya. Hozirda,
Mendel bo‘lmagan genetikaga doir ma’lumotlar molekulyar genetiklarning asosiy
foydalanadigan ma’lumotlar bazasidir. Umumiy qaraganimizda, Mendel
bo‘lmagan genetika matematikaga nimani taklif qilishi mumkinligi haqida gap
ketsa, javob “Evolyutsiya algebralar”dir deymiz [22].
Bu yo‘nalishdagi ko‘plab natijalarni Yu.I.Lyubichning asarlaridan topish
mumkin. U tomonidan birinchi marta 1992 yilda evolyutsion algebralar sinfi
(evolutionary algebras nomi bilan) taklif qilingan. 2006 yilda J.P.Tian o‘zining
monografiyasida evolyutsion algebraning yangi turini taqdim yetdi. U o‘zinig
ilmiy ishlarida bu algebralar nazariyasining asoslarini yaratdi. Shundan so‘ng
evolyutsion algebralarga qiziqish keskin ortib ketdi. Evolyutsion algebra
tushunchasi algebralar va dinamik sistemalar orasida yotadi. Algebraik jihatdan
evolyutsion algebralar noassotsiativ Banax algebralari bo‘lsa, dinamik jihatdan
diskret dinamik sistemani ifodalaydi.
J.P.Tian o‘zining “Evolution Algebras and their Applications” nomli asarida
bu algebraning paydo bo’lishiga nimalar turtki bo‘ganligi haqida quyidagi fikrlarni
aytadi: Men stoxastik jarayonlar va genetikani o‘rganar ekanman, populyatsiya
genetikasi, bakteriofaglar ishtirokidagi bakteriyalarni ko‘paytirish, jinssiz
ko‘payish yoki umuman nomendel irsiyatida, Markov zanjirlarida va neytral Rayt-
Fisher modellari ortida ichki va umumiy matematik tuzilma borligi xayolimga
keldi. Shuning uchun biz uni yangi algebra turi, evolyutsiya algebra sifatida
kiritdik.
24

Evolyutsiya algebralari assosiativ va darajali-assosiativ bo‘lmagan Banach
algebralaridir. Darhaqiqat, ular assosiativ bo‘lmagan to‘liq normalangan
algebralarning tabiiy misollaridir. Ma’lum bo‘lishicha, bu algebralar juda ko‘p
o‘ziga xos xususiyatlarga ega, shuningdek, matematikaning boshqa sohalari,
jumladan, Graflar nazariyasi (xususan, tasodifiy graflar va tarmoqlar), Gruppalar
nazariyasi, Markov jarayonlari, dinamik sistemalar, tugunlar nazariyasi, va
Riemann-zeta funktsiyasini o‘rganish (yoki uning Ihara-Selberg zeta funktsiyasi
deb ataladigan versiyasi) kabi sohalar bilan aloqaga ega. Evolyutsiya
algebralarining noodatiy xususiyatlaridan biri shundaki, ular evolyutsiya
operatoriga ega. Ushbu evolyutsiya operatori evolyutsion algebralarining dinamik
ma’lumotlarini ochib beradi. Biroq, evolyutsion algebralar nazariyasining
algebralarning klassik nazariyasidan farq qiladigan farqi shundaki, evolyutsion
algebralarda ikki xil turdagi generatorlar (bazislar) bo‘lishi mumkin: algebraik
barqaror generatorlar va algebraik o‘tkinchi generatorlar.
Yuqorida aytib o‘tganimizdek, evolyutsion algebralar matematikaning va fanning
ko‘plab sohalari bilan aloqalarga ega. Evolyutsion algebralardan foydalanib, biz
ko‘plab matematik sohalardagi muammolarni yangi nuqtai nazardan ko‘ra olamiz.
Tadqiqotlarning aksariyati nazariy jihatdan ham, amaliy jihatdan ham juda
qiziqarli va istiqbolli hisoblanadi.
2.2 - § . EVOLYUTSION ALGEBRALAR VA ULARNING XOSSALARI
Evolyutsion algebralar haqida fikrlarimizni davom etttirishdan oldin dastlab
biologiyadan ma’lum bo‘lgan ba‘zi tushunchalarni beramiz. Populyatsiya - bu bir
xil turdagi, uzoq vaqt davomida bir hududda (ma’lum bir hududni egallagan)
yashaydigan va boshqa bir xil guruhlardan butunlay ajratilgan organizmlar
to‘plamidir. Bu sohaga doir fanlarda odatda populyatsiya dinamikasi bo‘limi
dinamik sistema sifatida populyatsiyalarning kattaligi va yosh tarkibini o‘rganadi.
Aholi dinamikasini o‘rganish yo‘nalishi ikki yuz yildan ortiq tarixga ega bo lganʻ
matematik biologiyaning yaxshi rivojlangan bo limlaridan biridir [5, 7, 10, 20].
ʻ
Gen bu tirik organizm irsiyatining molekulyar birligi hisoblanadi. Allel esa bir xil
25

genning bir qator muqobil shakllaridan biridir. Masalan, odamlarda qon guruhini
aniqlaydigan genda uch xil allel mavjud.
Muayyan populyatsiya uchun asosiy matematik muammo populyatsiyaning
evolyutsiyasini (vaqtga bog'liq dinamikani) sinchkovlik bilan o'rganishdir. Bu
masalani o rganishda qo llaniladigan matematik usullar ehtimollar nazariyasi,ʻ ʻ
stokastik jarayonlar, dinamik tizimlar, chiziqli bo lmagan differensial va ayirma
ʻ
tenglamalar, assotsiativ bo lmagan algebralarga asoslanadi [14, 15, 27, 33, 36].
ʻ
2010 yilda J.M.Casas, M.Ladra va U.A.Rozikovlar tomonidan ilk bor
evolyutsion algebralarning zanjiri tushunchasi kiritildi va bunday zanjirlarning
keng sinfi qurildi. Bu zanjir har bir berilgan vaqt momentida evolyutsion algebrani
hosil qiladigan dinamik sistemadir. Bunday zanjirlar B.A.Omirov,
K.M.Tulenbayev, M.Ladra, Sh.N.Murodov, M.V.Velasko, A.N.Imomkulovlar
tomonidan ham qurilgan va ularning ba‘zi xossalari o‘rganilgan. Shuningdek, 2016
yilda M.Ladra va U.A.Rozikovlar tomonidan evolyutsion algebralarning zanjiri
tushunchasining umumlashmasi sifatida chekli o‘lchamli algebralar oqimi
tushunchasi kiritildi. Ushbu sohadagi natijalar haqida umumiy ma’lumotlarni
U.A.Rozikovning «Populyatsiya dinamikasi» nomli kitobidan topishimiz mumkin.
Yo.K.Kasado, M.S.Molina va M.V.Velaskolar tomonidan uch o‘lchamli
evolyutsion algebralar tasniflangan. Ular xarakteristikasi ikkidan farq qiluvchi va
ixtiyoriy
xn−k , n = 2, 3, 7 va k ∈ K
ko‘rinishdagi ko‘phad ildizga ega bo‘ladigan K
maydon ustida aniqlangan evolyutsion algebralarni o‘rgangan va bunday
algebralar izomorfizm aniqligida jami 116 ta ekanligini isbotlashgan [8].
Sh.N.Murodovning ishlarida [28, 29] evolyutsion algebralarning ikki o‘lchamli
zanjirlardagi tasniflari o‘rganilgan. Bu kabi tasnif uch o‘lchamli evolyutsion
algebralar zanjirlarida B.A.Narkuziyev va U.A.Rozikovlarning ilmiy ishlarida
qaralgan [30, 34]. Chekli o‘lchamli algebralarni evolyutsion algebralar bilan
yaqinlashtirish masalasi A.N.Imomkulov tomonidan o‘rganilgan [21]. Shuningdek,
u tomonidan kvadratining o‘lchami birga teng bo‘lgan uch o‘lchamli haqiqiy
evolyutsion algebralar tasnifi topilgan va juft-jufti bilan o‘zaro izomorf bo‘lmagan
o‘n ikkita algebra mavjudligi ko‘rsatilgan.
26

Evolyutsion algebralar ilk bor J.P.Tianning kitobida keltirilgan, u bu
algebralarni genetika evolyutsiya qonunlari bilan asoslagan [35]. U allellarni
evolyutsion algebraning bazislari deb hisobladi va ikkita allel ei va ej larning
ko‘paytmasini aniqladi. Genetikada aniqlangan bunday ko‘paytma algebradagi
ko‘paytirishni ifodalaydi.
2.2.1-ta’rif. ( E , · )
biror maydon ustida aniqlangan algebra bo‘lsin. Agar
ei·ej=
{
0,agar ⅈ≠ j
∑k=1
n
aikek,agar i= j
shartni qanoatlantiruvchi e
1 , e
2 , … , e
n bazis majud bo‘lsa u holda bu algebraga
evolyutsion algebra deyiladi. Bu bazisga esa tabiiy bazis deyiladi.
M =(aij)
orqali evolyutsion algebraning strukturaviy o‘zgarmaslar matritsasini
belgilaymiz.
Endi, evolyutsion algebralarning bir nechta asosiy xossalarini muhokama
qilaylik. Ular evolyutsion algebraning ta’rifining natijasidir.
2.2.1-natija.
1) Evolyutsion algebralar umumiy holda assotsiativ emas.
2) Evolyutsion algebralar umumiy holda darajali-assosiativ emas.
3) Evolyutsion algebralar kommutativ va moslashuvchan.
4) Evolyutsion algebralarning to‘g‘ri yig‘indisi yana evolyutsion algebra.
5) Evolyutsion algebralarning Kronecker ko‘paytmasi yana evolyutsion
algebra bo‘ladi.
Isbot. Biz doimo
{e1,e2,… ,en} bazislar majmuasi bilan ishlaymiz va
evolyutsion algebralarni notrivial deb hisoblaymiz.
1) Umumiy holda, ba’zi
i indekslar uchun ⅈ≠ j bo‘lganda e
i · e
i =
∑
j = 1n
a
ij e
j va aij
lar ichida noldan farqlisi topiladi, chunki algebramiz notrivial. U holda
( e
¿ ¿ i · e
i ) · e
j ≠ 0 ¿
. Ammo e
i ·
( e
i · e
j ) = e
i · 0 = 0
. Ya’ni
( e
¿ ¿ i · e
i ) · e
j ≠ e
i ·
( e
i · e
j ) , ¿
bu evolyutsion algebralar umumiy holda assotsiativ emasligini anglatadi.
2) Biror
ei bazisni olamiz,
27

( e
¿ ¿ i · e
i ) · ( e
¿ ¿ i · e
i ) =
∑
k = 1n
a
ik e
k ·
∑
l = 1n
a
il e
l =
∑
k = 1n
a
ik 2
e
k2
¿ ¿((e¿¿i·ei)·ei¿·ei=(∑k=1
n
aikek)·ei)·ei=(aiiei2)·ei=¿
¿
( a
ii ∑
k = 1n
a
ik e
k ) · e
i = a
ii2
e
i 2
.
Umumiy holda
(e¿¿i·ei)·(e¿¿i·ei)≠¿¿¿
Demak, Evolyutsion algebralar umumiy holda darajali-assosiativ emas.
3) Evolyutsion algebradagi ixtiyoriy x
va
y elementlarni olamiz,
x=∑i=1
n
xiei
va y =
∑
j = 1n
y
j e
j .
U holda
x · y =
∑
i = 1n
x
i e
i ·
∑
j = 1n
y
j e
j =
∑
i , j = 1n
x
i y
j e
i · e
j = ¿
∑
i , j = 1n
x
i y
i e
i2
= y · x . ¿
Demak, ixtiyoriy evolyutsion algebra kommutativ algebra ekan.
Agar algebraning ixtiyoriy
x,y elementlari uchun x ( yx ) = ( xy ) x
tenglik
bajarilsa, u holda algebra moslashuvchan (flexible) deyiladi. Shuni ta’kidlash
joizki, kommutativ algebra moslashuvchan bo‘ladi. Haqiqatan, kommutativ
algebra uchun
x(yx )= x(xy )=(xy )x . Shuning uchun ixtiyoriy evolyutsion algebra
moslashuvchan algebra ekan.
4) Mos ravishda
{ e
i | i ∈ Λ
1 }
va { η
j | j ∈ Λ
2 }
bazislar to‘plamlari bilan
berilgan
E1 va E2 evolyutsion algebralarni qaraymiz. U holda ushbu E1⊕E2 to‘g‘ri
yig‘indi
{ei,ηj|i∈Λ1,j∈Λ2} bazislar to‘plamiga ega bo‘ladi va ei ni (ei,0) , ηj ni esa
( 0 , η
j )
ko’rinishda aniqlaymiz. O‘z navbatida bu bazislar to‘plami E
1 ⊕ E
2 uchun
tabiiy bazislar to ‘ plami bo ‘ ladi. Buni quyidagicha tekshirishimiz mumkin:
ei·ei=∑k=1
n
aikek,
e
i · e
j = 0 , agar i ≠ j b o '
lsa ,
28

η
i · η
i =
∑
k = 1n
b
ik η
k ,
η
i · η
j = 0 , agar i ≠ j b o '
lsa ,ei·ηj= 0.
Shuning uchun
E1⊕E2 evolyutsion algebra bo‘ladi. E1⊕E2 ning o ‘ lchami E1 va E2
evolyutsion algebralarning o‘lchamlari yig‘indisiga teng bo‘ladi. To‘g‘ri yig‘indida
qo‘shiluvchilar soni 2 dan katta bo‘lgan holda ham isbot shu kabi bajariladi.
5) Mos ravishda
{ e
i | i ∈ Λ
1 }
va { η
j | j ∈ Λ
2 }
bazislar to‘plamlari bilan
berilgan
E1 va E2 evolyutsion algebralarni olamiz. E1 va E2 ikkita vektor
fazolarning E
1 ⨂ E
2 tenzor ko‘paytmasida odatdagi yo‘l bilan ko‘paytmani
aniqlaymiz. Ya’ni, x
1 ⨂ x
2 va y
1 ⨂ y
2 lar uchun
( x
1 ⨂ x
2 ) ·( y
1 ⨂ y
2 ) = x
1 y
1 ⨂ x
2 y
2
ifodani aniqlaymiz. Bu holda biz ikkita algebraning Kronecker ko‘paytmasiga ega
bo‘lamiz. Bu Kronecker ko‘paytma ham evolyutsion algebra bo‘ladi, chunki
Kronecker ko‘paytma uchun bazislar to ‘plami
{ e
i ⨂ η
j | i ∈ Λ
1 , j ∈ Λ
2 }
dan iborat. Ular
o‘ratsida aniqlangan munosabat quyidagicha bo‘ladi:
(ei⨂ ηj)·(ei⨂ ηj)≠0,
(ei⨂ ηj)·(ek⨂ ηl)=0,agar i≠kyoki j≠lbo'lsa .
Bu algebraning o ‘lchami uchun ushbu dim
( E
1 ⨂ E
2 ) = dim ( E
1 ) · dim ( E
2 )
tenglik o
‘rinli, ya’ni
E1⨂ E2 ning o‘lchami har bir E1 va E2 ning o‘lchamlari ko‘paytmasiga
teng. Ko‘paytuvchilar soni 2 dan katta bo‘lgan holda ham isbot shunga o‘xshash.
Evolyutsion algebraning xossalarini yaxshiroq tushunish uchun ikki
o’lchamli hol uchun quyidagi misolni qaraylik.
2.2.1- misol . Quyidagi bazislar ko‘paytmasi bilan berilgan evolyutsion
algebrani qaraymiz:
{
e
1 · e
1 = e
1 + 2 e
2
e
1 · e
2 = e
2 · e
1 = 0
e
2 · e
2 = 3 e
1 − e
2 .
Assosiativlikni tekshirib ko’rsak, ( e
1 · e
1 ) · e
2 va e
1 · ( e
¿ ¿ 1 · e
2 ) ¿
ko ‘paytmalarni
qaraylik:
(e1·e1)·e2=(e1+2e2)·e2=e1·e2+2e2·e2=¿
¿ 0 + 2
( 3 e
1 − e
2 ) = 6 e
1 − 2 e
2 ,
29

e1·(e¿¿1·e2)=e1·0=0.¿Demak,
(e1·e1)·e2≠e1·(e¿¿1·e2)¿ ekan.
Darajali-assosiativlikni tekshirib ko’raylik. Buning uchun
(e1·e1)·(e1·e1) va
(
( e
1 · e
1 ) · e
1 ) · e
1 ko‘paytmalarni qaraymiz.
(
e
1 · e
1 ) ·( e
1 · e
1 ) = ( e
¿ ¿ 1 + 2 e
2 ) · ( e
¿ ¿ 1 + 2 e
2 ) = ¿ ¿ ¿
¿e1·e1+2e1·e2+2e2·e1+4e2·e2= ¿
¿ e
1 + 2 e
2 + 4
( 3 e
1 − e
2 ) = 13 e
1 − 2 e
2 ,
endi ikkinchi ko ‘paytmani qaraymiz
((e1·e1)·e1)·e1=((e1+2e2)·e1)·e1=¿
¿
( e
1 · e
1 + 2 e
2 · e
1 ) · e
1 = ( e
1 + 2 e
2 ) · e
1 = e
1 · e
1 + 2 e
2 · e
1 = e
1 + 2 e
2 .
Bundan
(e1·e1)·(e1·e1)≠((e1·e1)·e1)·e1 ekanligini hosil qilamaiz. Ya’ni evolyutsion
algebralar umumiy holda darajali-assosiativ emas.
Kommutativlik
e1·e2= e2·e1 ekanligidan kelib chiqadi. Umuman ixtiyoriy
algebraning kommutativ algebra bo‘lishi uchun bazislar ko‘paytmasida ixtiyoriy i
va
j uchun
ei·ej=ej·ei
tenglikning bajarilishi zarur va yetarli.
Yuqorida ko‘rsatilganidek, bu kommutativ algebra moslashuvchan ham
bo‘ladi.
Umumiy holda evolyutsion algebralar assosiativ va darajali-assosiativ emas
ekan. Assosiativ va darajali assosiativ evolyutsion algebralar mavjudmi? Agar
mavjud bo‘lsa ularga misollar tuzish mumkinmi? Bu savollarga javob topish
albatta qiziqarli. Bu savollarga quyidagicha javob beramiz:
Assosiativ va darajali assosiativ evolyutsion algebralar mavjud va bunday
algebralarga quyidagi keltiradigan algebramiz misol bo‘la oladi .
2.2.2-misol. Quyidagi bazislar ko‘paytmasi bilan berilgan evolyutsion
algebrani qaraymiz:
{
e1·e1=e1
e1·e2=e2·e1=0
e2·e2= e2.
30

Bu algebramiz assosiativ va darajali assosiativ evolyutsion algebra bo‘la oladi.
Haqiqatan, assosiativlikni tekshirish ushbu (e1·e1)·e1= e1·(e¿¿1·e1),¿
(e1·e1)·e2=e1·(e¿¿1·e2)¿ ,
(
e
1 · e
2 ) · e
1 = e
1 · ( e
¿ ¿ 2 · e
1 ) , ¿
( e
2 · e
1 ) · e
1 = e
2 · ( e
¿ ¿ 1 · e
1 ) ¿
,
(e1·e2)·e2= e1·(e¿¿2·e2),(e2·e2)·e1= e2·(e¿¿2·e1),¿¿

(e2·e1)·e2= e2·(e¿¿1·e2),¿
(e2·e2)·e2=e2·(e¿¿2·e2)¿
tengliklarning bajarilishini tekshirish demakdir. Bu tengliklar bizning tuzgan
misolimiz uchun o‘rinli.
Drajali-assosiativlik ham o‘rinli, uni quyidagicha isbotlashimiz mumkin.
Ushbu tenglik
( e
i · e
i · … · e
i )
⏟
n
1 · ( e
i · e
i · … · e
i ) ⏟
n
2 · … · ( e
i · e
i · … · e
i ) ⏟
n
k = e
i
n1,n2,… ,nk∈{1,2 ,… ,n−1}
larning ixtiyoriy qiymatlarida, i=1yoki 2 bo‘lganda
doimo o‘rinli. Bu esa algebraning darajali assosiativ evolyutsion algebra
bo‘lishini anglatadi.
2.3- §. ABSOLYUT NILPOTENT VA IDEMPOTENT ELEMENTLAR
Evolyutsion algebraning absolyut nilpotent va idempotent elementlari haqida
fikrlarimizni aytishdan oldi, dastlab umumiy holda biror halqaning nilpotent va
idempotent elementlari tushunchasiga to‘xtalsak [2].
Bizga
R halqa berilgan bo‘lsin. Uning ixtiyoriy a∈R elementi va n butun son uchun
na
elementni quyidagicha aniqlaymiz:
0a=0,na =a+a+… +a ⏟ ,n>0,na =(−n)(− a),n<0.nta
Halqaning ixtiyoriy a , b ∈ R
elementlari va ixtiyoriy m , n
butun sonlar uchun
quyidagi xossalar o‘rinli ekanligi osongina kelib chiqadi:
(m+n)a= ma +na ,m(a+b)= ma +mb
(mn )a=m (na ),m (ab )= (ma )b= a(mb ),(ma )(nb )=mn (ab )
2.3.1-ta’rif. Agar shunday n
natural soni mavjud bo‘lib, ixtiyoriy a
element
uchun
na =0 tenglik o‘rinli bo‘lsa, u holda bu shartni qanoatlantiruvchi eng kichik
31

$natural songa, halqaning xarakteristikasi deb ataladi. Agar bunday natural son mavjud bo‘lmasa, u holda halqaning xarakteristikasi nolga teng deyiladi. Masalan, Z, Q, R, C halqalar xarakteristikasi nolga teng bo‘lgan halqalar bo‘lsa, Z n halqa esa, xarakteristikasi n ga teng bo‘lgan halqadir. Quyidagi misolda xarakteristikasi 2 ga teng bo‘lgan halqaga misol keltiramiz. 2.3.1-misol. Ixtiyoriy bo‘sh bo‘lmagan X to‘plamning qism to‘plamlaridan tuzilgan P ( X ) to‘plamlar oilasini qaraymiz. Ma’lumki, P ( X ) to‘plam simmetrik ayirma amaliga nisbatan kommutativ gruppa tashkil qiladi. Agar (P(X ),∆,∩) uchlikni qarasak, u holda bu uchlik halqa tashkil qiladi, ya’ni P ( X ) to‘plam simmetrik ayirma va kesishma amallariga nisbatan halqa tashkil qiladi. Bu halqa kommutativ, birlik elementga ega halqa bo‘lib, nol element vazifasini bo‘sh to‘plam bajaradi, ya’ni 0 = ∅ . Ushbu halqaning xarakteristikasi 2 ga teng, chunki 2A = A ∆ A = (A \ A) ∪ (A \ A) = ∅ . Quyidagi teoremada butunlik sohasining xarakteristikasi qanday songa teng bo‘lishi mumkinligi haqida ma’lumot beramiz. 2.3.1-teorema . Butunlik sohasining xarakteristikasi faqat nolga yoki tub songa teng bo‘ladi. Isbot . Faraz qilaylik, R butunlik sohasi chekli xarakteristikaga ega bo‘lib, u murakkab n soniga teng bo‘lsin. U holda n= n1n2,1<n1,n2<n hamda ixtiyoriy a∈R uchun na = 0 , xususan n 1 = 0 . U holda 0=n1=(n1n2)1=(n11)(n21) bo‘ladi . R nolning bo‘luvchisiga ega bo‘lmaganligi uchun n11= 0 yoki n21=0 . Agar n11= 0 bo‘lsa, u holda ixtiyoriy a∈R uchun n1a= n1(1a)=(n11)a=0 . Bu esa, halqaning xarakteristikasi n ekanligiga, ya’ni n ning minimalligiga zid. Xuddi shunday, n 2 1 = 0 ekanligidan ham ziddiyat kelib chiqadi. Demak, n tub son. Endi halqaning nilpotent va idempotent elementlari tushunchalarini kiritamiz. 2.3.2-ta’rif . Agar halqaning a∈R elementi uchun a 2 = a shart bajarilsa, u holda bu element idempotent element deb ataladi. Agar qandaydir n natural son uchun an=0 bo‘lsa, u holda bu element nilpotent element deb ataladi. Halqaning nilpotent va idempotent elementlari uchun quyidagi sodda xossalar o‘rinli. 32$

1. Agar noldan farqli a∈R element idempotent bo‘lsa, u holda u nilpotent
emas.
2. Agar
a∈R element nilpotent bo‘lsa, u holda u teskarilanuvchi emas.
3. Agar a ∈ R
element nilpotent bo‘lsa, u holda u nolning bo‘luvchisi bo‘ladi.
4. Agar
R kommutativ halqa bo‘lib, a va b elementlar nilpotent bo‘lsa, u holda
a + b
ham nilpotent bo‘ladi.
5. Agar
R birlik elementli, nolning bo‘luvchilariga ega bo‘lmagan halqa bo‘lsa,
u holda halqaning 0 va 1 dan boshqa idempotent elementlari mavjud emas.
2.3.2 -misol. Z
12 halqaning idempotent elementlari 0, 1, 4 va 9, nilpotent
elementlari esa 0 va 6 lardan iborat bo‘ladi.
Endi evolyutsion algebraning absolyut nilpotent va idempotent elementlari
haqida fikrlarimizni bayon qilsak [33].
2.3.3-ta’rif . Algebraning
x elementi uchun
x 2
= 0 tenglik o‘rinli bo‘lsa, u
absolyut nilpotent element deyiladi.
Yuqorida keltirilgan idempotent element ta’rifida esa,
x2= x tenglik bajarilishi
lozim. Absolyut nilpotent va idempotent elementlar genetik algebralar va
evolyutsion algebralarning muhim elementlari hisoblanadi. Ularning biologik
jihatdan ahamiyati mos ravishda biror turning yoki uning biror xossasining ma’lum
bir davrdan keyin butunlay yo‘qolib ketishi yoki takrorlanishi bilan izohlanadi.
Shuning uchun ham bu elementlarni o‘rganish bu yo‘nalishning muhim
masalalaridan biridir.
33

III.BOB. EVOLYUTSION ALGEBRALARNING TADBIQLARI
3.1- §. EVOLYUTSION ALGEBRANING BIOLOGIYAGA TADBIQI
Evolyutsion algebraning biologiyaga tadbiqini ko‘rishda dastlab ayrim
biologik tushuncha va ta’riflarga to‘xtalsak [40].
Prokariotlar - bir hujayrali organizmlar bo ‘ lib, ular yer yuzidagi hayotning
eng qadimgi va eng ibtidoiy shakllaridir (3.1.1-rasm). Prokariotlar bakteriyalar va
arxeylarni (ular bakteriyalardan farq qiladi, a rxeylar 1970-yillarning boshlarida
kashf etilgan mikroskopik organizmlar guruhidir, ko ‘ pchiligi ekstremal
organizmlar bo ‘ lib, ular juda issiq, kislotali yoki ishqoriy muhit kabi eng ekstremal
sharoitlarda yashaydi va rivojlanadi ) o ‘ z ichiga oladi. Ba’zi prokariotlar, masalan,
siyanobakteriyalar fotosintez qiluvchi organizmlardir. Ko ‘ pgina
prokariotlar ekstremofil bo ‘ lib, har xil turdagi ekstremal muhitda, shu jumladan
gidrotermal teshiklarda, issiq buloqlarda, botqoqlarda, odamlar va hayvonlarning
ichaklarida ( Helicobacter pylori ) yashashi va rivojlanishi mumkin. Prokariotik
bakteriyalarni deyarli hamma joyda topish mumkin va ular inson
mikrobiotanasining bir qismidir. Ular sizning teringizda, tanangizda va
atrofingizdagi kundalik narsalarda yashaydilar.
3.1.1-rasm
34

Eukariotlar (yunoncha: eu yaxshi, haqiqiy, butun va karion — yadro degan
ma’nolarni beradi) — to ‘ liq shakllangan, haqiqiy yadroga ega bo ‘ lgan hujayrali
organizmlar. Eukariotlarga suvo ‘ tlar, yuksak o‘simliklar, barcha hayvonlar,
zamburug‘lar kiradi.
Barcha tirik organizmlarni hujayralarining asosiy tuzilishiga qarab ikki
guruhdan biriga ajratish mumkin: prokariotlar va eukariotlar. Prokariotlar yuqorida
ta’kidlaganimizdek hujayra yadrosi yoki membrana bilan qoplangan organellalar
mavjud bo ‘ lmagan hujayralardan tashkil topgan organizmlar. Eukariotlar esa
genetik materialni , hamda membrana bilan bog ‘ langan organellalarni saqlaydigan,
membrana bilan bog ‘ langan yadroga ega bo ‘ lgan hujayralardan tashkil topgan
organizmlardir.
Prokariotlarning ko‘payish jarayoni. Prokariotlar jinsiy bo ‘ lmagan
reproduktiv organizmlardir. Prokariotik hujayralar, eukaryotik hujayralardan farqli
o‘laroq, yadroga ega emas. Genetik material (DNK) nukleoid deb ataladigan
hududda to‘plangan va bu hududni hujayraning qolgan qismidan ajratib turadigan
membrana yo‘q. Prokariot merosida mitoz va meioz bo‘lmaydi. Buning o‘rniga
prokariotlar ikkilik bo‘linish orqali ko‘payadi. Ya’ni, prokariotik xromosoma
ko‘payib, hujayra kattalashgandan so‘ng, kattalashgan hujayra, hujayra devori
bilan bo‘lingan ikkita kichik hujayraga aylanadi. Asosan, bir avloddan ikkinchisiga
o‘tadigan genetik ma’lumot DNKning o‘z-o‘zini replikatsiyasining qat’iyligi
tufayli saqlanishi kerak. Biroq, atrof-muhitda genetik ma’lumotlarning avloddan-
avlodga o‘zgarishiga olib kelishi mumkin bo‘lgan ko‘plab omillar mavjud.
Prokariotlarning irsiyati Mendel genetikasiga bo‘sunmaydi. Birinchi omil - bu
DNK mutatsiyasi (3.1.2-rasm).
Ikkinchi omil prokariotik gen va virusli gen o‘rtasidagi gen rekombinatsiyasi bilan
bog‘liq, masalan, bakteriofagning geni shunday xususiyatga ega. Prokariotik gen
va virus gen o‘rtasidagi rekombinatsiya jarayoni gen transduksiyasi deb ataladi.
Transduktsiyaning batafsil jarayoni Nell Kempbellning ishlarida keltirilgan [31].
Uchinchi omil jinsiy plazmidlar tomonidan qo‘zg‘atilgan konjugatsiyadan kelib
chiqadi.
35

3.1.2-rasm
Ya’ni bu ikkita prokariotik hujayralar o‘rtasida genetik materialning to‘g‘ridan-
to‘g‘ri uzatilishidir. Eng ko‘p o‘rganilgan holat bu - ichak tayoqchasidir, 3.1.3-
rasmda bakterial hujayraning bo‘linishi tasvirlangan [31].
Keling, jinsiy bo‘lmagan ko‘payish jarayonini matematik tarzda tuzamiz.
Faraz qilaylik, bizda genetik jihatdan bir-biridan farq qiluvchi n
ta prokariot
mavjud bo‘lib, ularni p1,p2,… ,pn bilan ifodalaylik. Shuningdek, biz bir xil atrof-
muhit sharoitlari avloddan-avlodga saqlanib qoladi deb taxmin qilamiz. Biz ikki
avlod davomida gen chastotalaridagi o‘zgarishlarni ko‘rib chiqamiz. Biz buni aholi
nuqtai nazaridan ham, individual nuqtai nazardan ham ko‘rishimiz mumkin.
Buning uchun biz quyidagi munosabatlarni o‘rnatishimiz mumkin:
{
p
i · p
j = 0 , ⅈ ≠ j ,
p
i · p
i =
∑
k = 1n
c
ik p
k .
Bu erda biz ko‘payishni jinssiz ko‘payish sifatida qaraymiz.
36

3.1.3-rasm
3.2- §. EVOLYUTSION ALGEBRANING FIZIKAGA TADBIQI
Evolyutsion algebraning fizikaga tadbiqini ko‘rib chiqaylik. Buning uchun
zarrachalar harakatlanadigan graf va uning uchlari, qirralari tushunchalarini
keltiramiz [40].
1736- yilda L.Eyler tomonidan o‘z davrning qiziqarli amaliy masalalardan
biri hisoblangan Kyonigsberg ko‘priklari haqidagi masalaning qo‘yilishi va
yechilishi graflar nazariyasining paydo bo‘lishiga olib keldi. Masalaning qo‘yilishi
quyidagicha: Shaharning ixtiyoriy qismida joylashgan uydan chiqib yettita
ko‘prikdan faqat bir martadan o‘tib yana o‘sha uyga qaytib kelish mumkinmi?
37

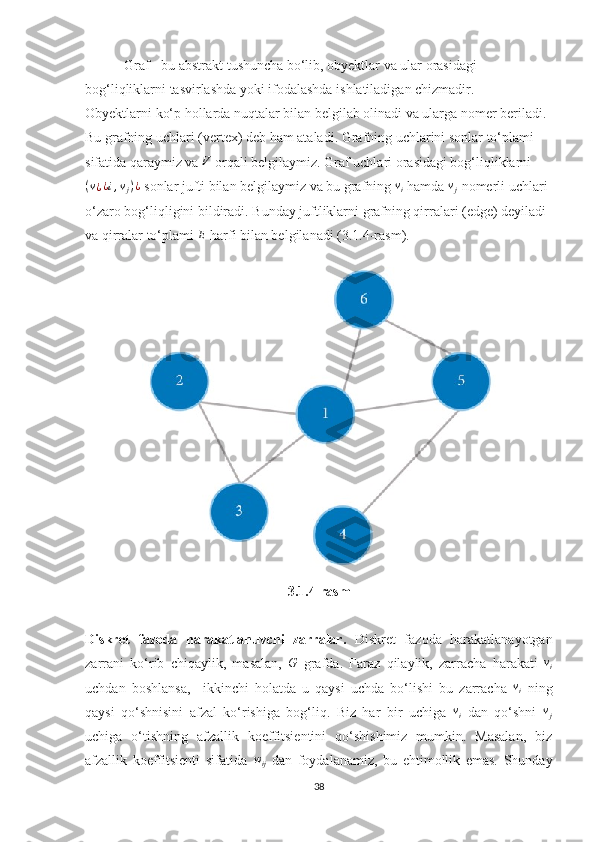
Graf - bu abstrakt tushuncha bo‘lib, obyektlar va ular orasidagi
bog‘liqliklarni tasvirlashda yoki ifodalashda ishlatiladigan chizmadir.
Obyektlarni ko‘p hollarda nuqtalar bilan belgilab olinadi va ularga nomer beriladi.
Bu grafning uchlari (vertex) deb ham ataladi. Grafning uchlarini sonlar to‘plami
sifatida qaraymiz va V orqali belgilaymiz. Graf uchlari orasidagi bog‘liqliklarni
(v¿¿i,vj)¿
sonlar jufti bilan belgilaymiz va bu grafning vi hamda vj nomerli uchlari
o‘zaro bog‘liqligini bildiradi. Bunday juftliklarni grafning qirralari (edge) deyiladi
va qirralar to‘plami E
harfi bilan belgilanadi (3.1.4-rasm).
3.1.4-rasm
Diskret fazoda harakatlanuvchi zarralar. Diskret fazoda harakatlanayotgan
zarrani ko‘rib chiqaylik, masalan,
G grafda. Faraz qilaylik, zarracha harakati vi
uchdan boshlansa, ikkinchi holatda u qaysi uchda bo‘lishi bu zarracha v
i ning
qaysi qo‘shnisini afzal ko‘rishiga bog‘liq. Biz har bir uchiga
vi dan qo‘shni vj
uchiga o‘tishning afzallik koeffitsientini qo‘shishimiz mumkin. Masalan, biz
afzallik koeffitsienti sifatida
wij dan foydalanamiz, bu ehtimollik emas. Shunday
38

qilib, ikkinchi pozitsiya bu zarracha eng ko‘p afzal ko‘rgan uch bo‘ladi. Bu
zarracha graf ustida uzluksiz harakat qiladi. Agar zarracha biron bir uchda to‘xtasa,
uning izi umumiy afzallik koeffitsientining maksimal qiymatiga ega bo‘lgan yo‘l
bo‘ladi. Endi bizni qiziqtirgan savol shundan iboratki, zarrachaning harakatini
algebraik tarzda qanday tasvirlash mumkin va boshlang‘ich uch va oxirgi uch
berilgandan so‘ng umumiy afzallik koeffitsientlari maksimal bo‘lgan yo‘lni qanday
topish mumkin. Ushbu muammolarni muhokama qilish uchun bazislar to‘plamini
va ular o‘rtasidagi munosabatlarni aniqlovchi ifodani quyidagi tarzda berib,
algebraik modelni o‘rnatishimiz mumkin.
Uchlar to‘plami V={v1,v2,… ,vr} ni bazislar to‘plami sifatida olsak, u holda
munosabatlarni aniqlovchi ifoda quyidagicha beriladi:
{
v
i · v
i =
∑
j = 1r
w
ij v
j
v
i · v
j = 0 , i ≠ j ,
Bu yerdagi w
ij va
wji afzallik koeffitsientlari turli bo‘lishi mumkin va i , j = 1,2 , … , r .

3.3- §. EVOLYUTSION ALGEBRANING EHTIMOLLAR
NAZARIYASIGA TADBIQI
Dastlab ehtimollar nazariyasi va matematik statistikada keng
qo‘llaniladigan Markov zanjirlari yoki jarayonlari tushunchasiga to‘xtalamiz [40].
Markov zanjiri yoki Markov jarayoni - bu har bir hodisaning ehtimoli faqat
oldingi hodisada erishilgan holatga bog‘liq bo‘lgan hodisalar ketma-ketligini
tavsiflovchi stoxastik modeldir (3.1.5-rasm).
Stoxastik jarayon - ketma-ket sodir bo‘ladigan tasodifiy hodisalarning
matematik tavsifi. Ushbu hodisalarni ular sodir bo‘lgan vaqtga qarab tartiblash
mumkin.
39

Holatlar to'plami S sanoqli bo‘lgan to‘plamda harakatlanadigan stoxastik
jarayonni ko‘rib chiqamiz.
n−¿ bosqichda jarayon oldingi holatga yoki hatto n
vaqtga emas, balki faqat joriy holatga bog‘liq ravishda tasodifiy mexanizm orqali
keyingi holatda qayerda bo‘lishini hal qiladi. Bu jarayonlar sanoqli holatlar
fazolarida Markov zanjirlari deb ataladi. Aniqrog‘i, X
n holatlar fazosi S =
{ s
i| i ∈ Λ }
,
bo‘lgan diskret vaqtli Markov zanjiri bo‘lsin, shuningdek o‘tish ehtimoli
pij= Pr {Xn+1= sj|Xn= si}
berilgan bo‘lsin. Bu yerda biz birinchi navbatda statsionar
Markov zanjirlarini ko ‘ rib chiqamiz. Keyin, biz bunday Markov zanjirini algebra
orqali qayta shakllantirishimiz mumkin. Bazislar to ‘ plami sifatida
S ni qabul qilish
va ular orasidagi munosabatlarni aniqlovchi ifodani quyidagicha:
{
s
i · s
i =
∑
j p
ij s
j
s
i · s
j = 0 , i ≠ j ,
aniqlash mumkin.
3.1.5-rasm
XULOSA
40

Ushbu bitiruv malakaviy ishimda zamonaviy algebraning keng o‘rganilayotgan
sohalaridan biri bo‘lgan evolyutsion algebra va uning tadbiqlarini o‘rgandim.
Jumladan evolyutsion algebraning xossalari, uning muhim elementlari hamda bu
algebraning biologiya, fizika va ehtimollar nazariyasiga tadbiqlarini o ‘ rgandim.
Mavzuning barcha nazariy ma’lumotlarini o’rganib, shu asosida qo‘yilgan masalal
o’rganildi.
Ushbu bitiruv malakaviy ishida quyidagilar o’rganildi. Dastlab abstrakt
algebra kursida muhim bo’lgan umumiy tushunchalar bilan tanishdim, jumladan
gruppa, halqa va maydon tushunchalari, ularga doir turli misollar o‘rganildi.
Vektor fazo va unga doir misollar, algebra tushunchasi, assosiativ va noassosiativ
algebralar hamda noassosiativ algebralarning yaxshi o‘rganilgan ayrim muhim
turlarini o‘rganildi. Sohaning asosiy predmeti bo‘lgan genetik va evolyutsion
algebralar, evolyutsion algebraning xossalari, uning muhim elementlari o ‘ rganildi
va ularning amaliy ahamiyatini izohlash, hamda evolyutsion algebraning
biologiyaga, fizikaga va ehtimollar nazariyasiga tadbiqlari o’rganildi.
Odatda umumiy holda evolyutsion algebralar noassosiativ va darajali-assosiativ
emas, bitiruv malakaviy ishida assosiativ va darajali-assosiativ evolyutsion
algebraga misol tuzildi.
Bitiruv malakaviy ishidagi natijalardan foydalanib quyidagi masalani qarash
mumkin: evolyutsion algebraning strukturaviy matritsalariga qanday shart
qo‘yilganda u assosiativ va darajali-assosiativ evolyutsion algebra bo‘ladi.
Oxirgi bobda evolyutsion algebraning biologiyaga, fizikaga va ehtimollar
nazariyasiga tadbiqlari o’rganildi. Hamda bu tadbiqlarning mohiyatini yaxshiroq
tushunish maqsadida ularga doir misollar va chizmalar keltirildi.

ADABIYOTLAR RO‘YXATI
41

1. Abraham V.M., Linearising quadratic transformations in genetic
algebras , Thesis ,Univ. of London ,1976.
2. Ayupov Sh.A., Omirov B.A., Xudoyberdiyev A.X., “ Abstrakt algebra ”
o’quv qo’llanma Toshkent-2022
3. Ayupov Sh.A., Omirov B.A., Xudoyberdiyev A.X., “ Chiziqli algebra ”
darslik Toshkent-2023.
4. Baur E., Zeit. Vererbungsl. 1, 330-251, 1909.
5. N. Bacäer, A short history of mathematical population dynamics , Springer-
Verlag London, Ltd., London, (2011).
6. Ballonoff P., Genetics and Social Structure , Dowden, Hutchinson& Ross,
Stroudsburg, PA. 1974.
7. E. Baur, Das Wesen und die Erblichkeitsverhältnisse der ”Varietates
albomarginatae hort.” von Pelargonium zonale . Zeitschr find Abst u
Vererbungsl 1 , (1909), 330-351.
8. Y.C. Casado, M.S. Molina, M.V. Velasco, Classiﬁcation of three-
dimensional evolution algebras, Linear Algebra Appl., 524 , (2017), 68-
108.
9. Cotterma C.W., A calculus for statistico –genetics , Dissertation, The Ohio
State University, OH. 1940.
10. C. Correns, Vererbungsversuche mit blass(gelb)grünen und
buntblättrigen Sippen bei Mirabilis jalapa, Urtica pilulifera und Lunaria
annua. Zeitschr f ind Abst u Vererbungsl 1 , (1909), 291-329.
11. Correns C., Zeit. Vererbungsl. 1, 291-329,1909.
12. Etherington I.M.H., Non-associative algebra and the symbolism of
genetics , Proc.Roy.Soc.Edinburgh B 61,24-42, 1941.
13. Gonshor H., Contributions to genetic algebras , Proc. Edinburg Math.Soc
(2), 273-279, 1973.
14. N.N. Ganikhodjaev, H. Akin, F.M. Mukhamedov, On the ergodic
42

principle for Markov and quadratic stochastic processes and its relations,
Linear Algebra Appl. 416 (2-3), (2006), 730–741.
15. N.N. Ganikhodjaev, On stochastic processes generated by quadric
operators, J. Theoret. Probab. 4 (4), (1991), 639–653.
16. Glivenkov V., Algebra Mendelienne comptes rendus (Doklady) de
I’Acad.des Sci. de I’URSS 4,(13) ,385-386, 1938 (in Russian).
17. Holgate P., Sequences of powers in genetic algebras , J. London Math.,
42, 489-496, 1967.
18. Holgate P., Selfing in genetic algebras , J.Math .Biology ,6, 197-206,
1978.
19. Hench I., Sequences in genetic algebras for overlapping generations ,
Proc. Edinburgh Math. Soc. (2) 18, 19-29, 1972.
20. A. Hillion, Mathematical theories of populations, What Do I Know ?
(French), 2258. Presses Universitaires de France, Paris, (1986), 128 pp.
21. A.N. Imomkulov, Classiﬁcation of a family of three dimensional real
evolution algebras, TWMS J. Pure Appl. Math., 10 (2), (2019), 225-238.
22. Jianjun (Paul) Tian& Petr Vojtechovskiy, Mathematical concepts of
evolution algebras in non-Mendelian genetics , Quasigroup and Related
System, Vol.24, pp111-122,2006.
23. Lyubich Y. I., Mathematical Structures in Population Genetics , Springer-
Verlag, New York, 1992.
24. Kostitzin V.A., Sur les coefficients mendelians d’heredite, Comptes
rendus de I’Acad. Des Sci . 206,883-885, 1938 ( in French ).
25. Mendel G., Experiments in plant-hybridization, Classic Papers in
Genetics , pages 1-20 ,J.A.Peter editor, Prentice-Hall Inc. 1959.
26. Murray R. Bremner, Lucia I. Murakami, Ivan P. Shestakov, “ Handbook
of Linear Algebra - Nonassociative Algebras ” , 2006, Chapman and
Hall/CRC.
27. F.M. Mukhamedov, N.N. Ganikhodjaev, Quantum quadratic operators
and processes . Lecture Notes in Mathematics, 2133. Springer, Cham,
43

(2015).
28. Sh. Murodov, Classiﬁcation dynamics of two-dimensional chains of
evolution algebras, International Jour. Math. 25 (02), (2014), 1450012.
29. Sh.N. Murodov, Classiﬁcation of two-dimensional real evolution
algebras and dynamics of some two-dimensional chains of evolution
algebras , Uzb. Mat. Jour . 2 , (2014), 102-111.
30. B.A. Narkuziyev, U.A. Rozikov, Classification in chains of three-
dimensional real evolution algebras , Linear and Multilinear Algebra,
2022.
31. Nell Campbell, Biology, fourth edition, the Benjamin Cummings
Company, Inc. 1996.
32. Reiser O., Genetic algebras studied recursively and by means of
differential operators , Math. Scand. 10, 25-44, 1962.
33. U.A.Rozikov, “ Population dynamics: algebraic and probabilistic
approach ” (World Sci. Publ. Singapore, (2020), 460 pp).
34. U.A. Rozikov, B.A. Narkuziyev, Classification of algebras in two chains
of real evolution algebras, Dok. Akad. Nauk. Uzbekistan, 2021, no. 04,
p.8-12.
35. Reed M.L., Algebraic structure of genetic inheritance , Bull. of AMS, 34,
(2), 107-130, 1997.
36. T.A. Sarymsakov, N.N. Ganikhodjaev, Analytic methods in the theory of
quadric stochastic operators , J. Theoret. Probab. 3 (1), (1990), 51-70.
37. Serebrowsky A., On the properties of the Mendelian equations , Doklady
A.N.SSSR. 2,33-36, 1934 (in Russian).
38. S loane N.J.A., and Wyner A.D., (editors) Claude Elwood Shannon
Collected Papers, IEEE Press, Piscataway , NJ. 1993
39. Schafer R.D., An introduction to non-associative algebras , Acad. Press,
New York , 1966.
40. J.P. Tian, Evolution algebras and their applications , Lecture Notes in
Mathematics, 1921, Springer-Verlag, Berlin, 2008.
44

41. Worz-Busekros A., Algebras in Genetics , Lecture Notes in Biomath. 36,
Springer-Verlag, Berlin , 1980.
45

“ EVOLYUTSION ALGEBRA VA UNING TADBIQLARI ” MUNDARIJA Kirish………………………………………………………………………………3 I.BOB. UMUMIY TUSHUNCHALAR. GRUPPA, HALQA, MAYDON VA VEKTOR FAZO TUSHUNCHALARI. ASSOSIATIV VA NOASSOSIATIV ALGEBRALAR 1.1 - § . Gruppa, halqa va maydon…………………………………………….......5 1.2 - § . Vektor fazo va unga misollar…………………………………………...14 1.3 - § . Algebra tushunchasi. Assosiativ va noassasiativ algebralar……………18 II.BOB. GENETIK VA EVOLYUTSION ALGEBRALAR. ABSOLYUT NILPOTENT VA IDEMPOTENT ELEMENTLAR 2.1 - § . Genetik va evolyutsion algebralar tarixi……………………………......21 2.2 - § . Evolyutsion algebralar va ularning xossalari…………………………...25 2.3 - § . Absolyut nilpotent va idempotent elementlar…………………………..31 III.BOB. EVOLYUTSION ALGEBRALARNING TADBIQLARI 3.1 - §. Evolyutsion algebraning biologiyaga tadbiqi………………..................33 3.2 - §. Evolyutsion algebraning fizikaga tadbiqi………………........................37 3.3 - §. Evolyutsion algebraning ehtimollar nazariyasiga tadbiqi……………...39 1. Xulosa ..........................................................................................................41 2. Foydalanilgan adabiyotlar ............................................................................42 1

KIRISH Bitiruv malakaviy ishining dolzarbligi: Ushbu bitiruv malakaviy ishimda zamonaviy algebraning keng o ‘ rganilayotgan sohalaridan biri bo ‘ lgan evolyutsion algebra va uning tadbiqlari o ‘ rganilgan. Jumladan evolyutsion algebraning xossalari, uning muhim elementlari hamda bu algebraning biologiya, fizika va ehtimollar nazariyasiga tadbiqlari o ‘ rganilgan. Bitiruv malakaviy ishining maqsadi: Evolyutsion algebraning xossalarini, uning muhim elementlarini hamda uning fizikaga, biologiyaga va ehtimollar nazariyasiga tadbiqlarini o ‘ rganishdan iboratdir. Bitiruv malakaviy ishining vazifalari: Bitiruv malakaviy ishining vazifalari evolyutsion algebraning xossalarini, uning muhim elementlarini o ‘ rganish va ularning amaliy ahamiyatini izohlash, hamda evolyutsion algebraning fizikaga, biologiyaga va ehtimollar nazariyasiga tadbiqlarini o’rganish, bu yo ‘ nalishga qizziqgan va o ‘ rganishni istagan talabalar, magistrlar va yosh olimlar uchun o ‘ zbek tilida yozilgan dastlabki muhim ma’lumotlar bazasini shakllantirishdan iborat. Bitiruv malakaviy ishining o ‘ rganilganlik darajasi: Ushbu malakaviy bitiruv ishida qo’yilgan talablar bajarildi, qo’yilgan vazifa yuzasidan ma’lumotlar o ‘ rganildi va ularning o ‘ zbek tilidagi dastlabki namunasi shakllantirildi. Gruppa, halqa va maydon haqidagi dastlabki muhim ma’lumotlar va ularga doir misollar, vektor fazo va unga misollarni o ‘ rganishda Sh.A.Ayupov, B.A.Omirov, A.X.Xudoyberdiyev “Abstrakt algebra” o ‘ quv qo ‘ llanmasidan, noassosiativ algebralarni o ‘ rganishda Murray R. Bremner, Lucia I. Murakami, Ivan P. Shestakovlarning “Nonassociative Algebras” nomli ilmiy asaridan, genetik va evolyutsion algebralar tarixi, evolyutsion algebralar, hamda bu algebralarning absolyut nilpotent va idempotent elementlarini o ‘ rganishda bu yo ‘ nalishda fundamental ma’lumotlar bazasini o ‘ zida mujassamlashtirgan Jianjun Paul Tianning “Evolution Algebras and their Applications” ilmiy asaridan, J.M.Casas, M.Ladra, B.A.Omirov va U.A.Rozikovlarning “On Evolution Algebras” nomli ilmiy maqolasidan, B.A.Narkuziyevning “ On absolute 2

nilpotent and idempotent elements of an evolution algebra corresponding to permutations” nomli maqolasidan va “Evolution algebras and their three- dimensional chains” nomli PhD dissertatsiya ishlari qaraldi. Evolyutsion algebralarning tadbiqlari haqidagi asosiy ma’lumotlarni o ‘ rganishda Jianjun Paul Tianning “Evolution Algebras and their Applications” ilmiy asariga hamda U.A. Rozikovning “Population dynamics: algebraic and probabilistic approach” (World Sci. Publ. Singapore, (2020), 460 pp) nomli ilmiy kitobiga tayanildi [33]. Bitiruv malakaviy ishining ob’yekti: Ushbu ishning ob’yekti evolyutsion algebraning xossalari, uning muhim elementlari va ularning amaliy ahamiyatini izohlash, hamda evolyutsion algebraning fizika, biologiya va ehtimollar nazariyasiga tadbiqlari o ‘ rganish, bu sohadagi dastlabki o ‘ zbek tilidagi ilmiy ma’lumotlarni to ‘ plash va bu sohani o’rganishni boshlagan yosh olimlarga sohaga kirish uchun fundamental ma’lumotlarni yetkazish hisoblanadi. Bitiruv malakaviy ishining predmeti: Evolyutsion algebralarning paydo bo ‘ lish tarixi, uning boshqa algebralardan farqi, uning xossalari va fanning turli sohalariga tadbiqlarini o ‘ rganish, shu paytgacha bu sohada to ‘ plangan ma’lumotlarni o ‘ zbek tilida o’quvchiga yetkazishdan iborat. Bitiruv malakaviy ishida qo ‘ llanilgan metodikaning tavsifi: Ishda chiziqli va abstrakt algebraning usullaridan, ilmiy tadqiqot ishlarini nazariy va amaliy jihatdan bog ‘ lashning tayanch usullaridan, hamda noassosiativ algebralarni o ‘ rganishning umumiy usullaridan foydalanilgan. Bitiruv malakaviy ishi mundarija, kirish, uchta bob, xulosa va adabiyotlar ro ‘ yxatidan iborat. Bitiruv malakaviy ishimda qo ‘ yilgan masala yuzasidan asosiy va yordamchi adabiyotlar o ‘ rganildi. Shuningdek, bu soha algebraning yangi va zamonaviy sohalaridan biri bo‘lganligi va bu yo ‘ nalishdagi dastlabki o ‘ zbek tilidagi fundamental ma’lumotlar to ‘ planganligi bilan ahamiyatlidir. 3

I.BOB. UMUMIY TUSHUNCHALAR. MAYDON VA VEKTOR FAZO TUSHUNCHALARI. ASSOSIATIV VA NOASSOSIATIV ALGEBRALAR. 1.1- §. GRUPPA, HALQA VA MAYDON Bizga bo‘sh bo‘lmagan A to‘plam va A × A dekart ko‘paytma berilgan bo‘lsin. A × A dekart ko‘paytmani A to‘plamga o‘tkazuvchi ∗ : A × A → A asklantirish berilgan bo‘lsa, u holda A to‘plamda binar amal aniqlangan deyiladi [2]. Ushbu (A, ∗ ) juftlikka esa algebraik sistema yoki gruppoid deb ataladi. Odatda (a, b) elementning bu akslantirishdagi qiymati a ∗ b, a · b yoki ab kabi belgilanadi. 1.1.1-misol. • Bizga biror A to‘plam berilgan bo‘lib, ushbu to‘plamdan olingan ixtiyoriy x va y elementlar uchun x ∗ y = x ko‘rinishda aniqlangan ∗ amali binar amal bo‘ladi. • N natural sonlar to‘plamida quyidagi amallar binar amal bo‘ladi: natural sonlarni qo‘shish, ko‘paytirish, ikki sonning maksimumi, minimumi, eng katta umumiy bo‘luvchisi va eng kichik umumiy karralisi. • Z butun sonlar to ‘ plamida qo ‘ shish (+) va ko ‘ paytirish (·) amallari binar amal bo’ladi. • [a, b] kesmada uzluksiz bo‘lgan barcha funksiyalar fazosi C[a, b] da ixtiyoriy f, g ∈ C [a, b] funksiyalar uchun (f ◦ g)(x) = f (g(x)) kabi aniqlangan funksiyalar kompozitsiyasi (superpozitsiya) deb ataluvchi amal binar amal bo‘ladi. 1.1.1-ta’rif . Agar (S, ∗ ) algebraik sistemada ixtiyoriy a, b, c ∈ S elementlar uchun assosiativlik xossasi, ya’ni (a ∗ b) ∗ c = a ∗ (b ∗ c) tenglik o‘rinli bo‘lsa, u holda (S, ∗ ) algebraik sistemaga yarim gruppa deyiladi. 1.1.2-misol . • (N, +), (N, ·), (Z, ·) algebraik sistemalar yarim gruppa bo‘ladi. • A to‘plamda olingan ixtiyoriy x, y elementlar uchun ∗ amali x ∗ y = x 5

O'xshashlar

KARRALI XOSMAS INTEGRALLAR VA ULARNING TADBIQLARI

GRAFLAR NAZARIYASI ELEMENTLARI VA ULARNING MASALALAR YECHISHGA TADBIQLARI

UMUMTA’LIM MAKTABLARI ALGEBRA KURSIDA KOMBINATORIKA ELEMENTLARINI O‘QITISH METODIKASI

Matritsalar algebrasining robototexnikada qo’llaniladigan ayrim mexanizmlarning maxsusliklarini tekshirishga tadbiqlari

KVADRATIK STOXASTIK JARAYONLAR BIR SINFI UCHUN TRAYEKTORIYALAR