logo
  1. Bosh sahifa
  2. Diplom ishlar
  3. Umumiy
  4. Fenwick daraxti

Fenwick daraxti

Yuklangan vaqt:

12.08.2023

Ko'chirishlar soni:

0

Hajmi:

286.8828125 KB
Ko'chirib olish
Mavzu: “Fenwick daraxti” MUNDARIJA KIRISH ........................................................................................................... 3 1.1.Daraxt tushunchasi. ............................................................................. 5 B daraxtda element izlash .............................................................................. 13 void btree_lookup(struct btree *tree, int key, ................................................ 13 struct btree **node, int *index) ..................................................................... 13 { ..................................................................................................................... 13 int i; ................................................................................................................ 13 for (i = 0; i < tree->nkeys && key > tree->key[i]; ) { ................................... 13 i++; ................................................................................................................ 13 } ..................................................................................................................... 13 if (i < tree->nkeys && key == tree->key[i]) { .............................................. 13 *node = tree; .................................................................................................. 13 *index = i; ...................................................................................................... 13 return; ............................................................................................................ 13 } ..................................................................................................................... 13 if (!tree->leaf) { ............................................................................................. 13 /* Disk read tree->child[i] */ ......................................................................... 13 btree_lookup(tree, key, node, index); ............................................................ 13 } else { ........................................................................................................... 13 *node = NULL; } .......................................................................................... 13 II.BOB. DARAXTNING STRUKTURALARI VA DASTURI. .................. 14 2.2. Fenwick daraxti dasturiy tahlili. ....................................................... 17 Ikkilik indeksli daraxt (Fenwick Tree) massivning prefiks yig'indisini tezda hisoblash uchun ishlatilishi mumkin bo'lgan samarali ma'lumotlar strukturasidir.Agar massivda mavjud qiymatlar o'zgaruvchan bo'lsa. m   . e   .qiymatlarni Fenwick daraxti yordamida o'zgartirish mumkin, bu juda foydali.Odatda, agar biz massivdagi 0 dan n gacha bo'lgan barcha raqamlarning yig'indisini hisoblamoqchi bo'lsak, biz indeks-0 dan boshlab har bir elementni ko'rib chiqamiz va indeks-n ga qadar barcha elementlarni qo'shishni davom ettiramiz. Bu O(n) vaqtini oladi va o'lcham juda katta bo'lsa va biz ko'p so'rovlarni bajarishimiz kerak bo'lganda samarali emas.Buning bir yechimi prefiks sum massividan foydalanishdir. Prefiks yig'indisi massivi oldindan hisoblangan massiv bo'lib, unda har qanday indeksdagi qiymat asl massivdagi 0 dan ushbu indeksgacha bo'lgan barcha raqamlar yig'indisiga teng bo'ladi. Agar bizdan x va y o'rtasidagi indekslarning umumiy yig'indisini olishni so'ragan so'rovni olsak, biz x-1 indeksidagi prefiks summasini y indeksidagi prefiks yig'indisidan ayirishimiz kerak, bu bizga x indekslaridagi elementlarning yig'indisini beradi. y ga. Bu faqat 2 ta operatsiyani oladi va shuning uchun biz O (1) vaqtida diapazon summasini olishimiz mumkin. Ammo diqqatga sazovor narsa shundaki, agar indeksdagi qiymat io'zgarsa, kattaroq indekslar uchun barcha prefiks summalari io'zgaradi va bu O(N) vaqtini oladi.Xulosa qilib aytadigan bo'lsak, birinchi yondashuv O(N)har qanday berilgan indekslar orasidagi barcha elementlarning yig'indisini hisoblash uchun vaqt talab etadi, ammo O(1)har qanday elementni yangilash uchun vaqt kerak bo'ladi. Prefiks yig'indisidan foydalangan holda ikkinchi yondashuvda, O(1)har qanday berilgan indekslar orasidagi barcha elementlarning yig'indisini hisoblash uchun vaqt kerak bo'ladi, lekin O(N)agar dastlabki massivdagi biron bir element o'zgargan bo'lsa, prefiks yig'indisi qatorini yangilash uchun vaqt kerak bo'ladi.Endi savol shundaki, ikkalamiz o'rtasida muvozanat bo'lishi mumkinmi? ya'ni, har qanday elementni yangilash vaqtida o'rtacha vaqt murakkabligi va prefiks summalarini hisoblash uchun o'rtacha vaqt murakkabligi bormi? Ikkilik indeksli daraxt yoki Fenwick daraxti bu savolning bir yechimidir. 21 ADABIYOTLAR RO’YXATI ...................................................................... 22 ILOVALAR ................................................................................................... 23 ILOVA 1. Modul N1 boshlang’ich kodi. ............................................... 23 KIRISH Mavzuning dolzarbligi . Bugungi kunda ma‘lumotlar oqimining ko‘pligi tufayli ularni qisqa vaqt ichida qayta ishlash muommosi ham ortib bormoqda. Hozirgi vaqtda axborot- kommunikasiya vositalari barcha turdagi tashkilot va muassasalarga shiddat bilan kirib kelmoqda. Axborotlarning haddan tashqari ko‘pligi bu axborotlarni saqlashda, qayta ishlashda, hamda har xil turdagi tizimlarni yaratish, ulardan keng foydalanishni va axborot tizimlari yaratishni talab qiladi. O‘zbekiston Respublikasi Prezidentining 2017 yil 7 fevraldagi PF-4947-son Farmoni bilan tasdiqlangan 2017-2021 yillarda O‘zbekiston Respublikasini rivojlantirishning beshta ustuvor yo‘nalishi bo‘yicha harakatlar strategiyasi mamlakatning davlat va jamiyat rivojlanishi istiqbolini strategik rejalashtirish tizimiga sifat jihatdan yangi yondashuvlarni boshlab berdi[1]. Unda belgilangan vazifalar sirasida ta‘lim va fan sohasini rivojlantirish ham aloxida ko‘zda tutilgan. O‘zbekiston Respublikasi birinchi Prezidentining 2012 yil 21 martdagi “Zamonaviy axborot-kommunikasiya texnologiyalarini yanada joriy etish va rivojlantirish chora-tadbirlari to‘g‘risida”gi PQ-1730 Qarori hamda “O‘zbekiston Respublikasida —Elektron ta‘lim milliy tarmog‘ini yaratish” investision loyihasini amalga oshirish chora-tadbirlari to‘g‘risida” gi PQ-1740 Qarori va me‘yoriy hujjatlar asosida algoritmik ta‘minot ishlab chiqish va joriy etish keng ko‘lamli hisoblanadi. Barcha tashkilot va muassasalarda avtomatlashtirilgan tizimlar yaratish ulardan keng ko‘lamda foydalanish uchun algoritmlash tillarini o‘rni katta hisoblanadi. Axborot tizimlari axborotni to‘plash, saqlash va qayta ishlash uchun, keng imkoniyatli maqsadlarda samarali foydalanish uchun xizmat qiladi. Zamonaviy axborotlashtirish tizimi, ma‘lumotlar integratsiyasi konsepsiyasiga asoslangan katta hajmdagi ma‘lumotlarni saqlash bilan tavsiflanadi va ko‘p sondagi foydalanuvchilarning turli xildagi talablariga javob berishi kerak bo‘ladi. Axborot tizimi va axborot texnologiyalarining avtomatlashtirilgan elementlarini qo‘llash va avtomatlashtirish asosida yangi axborot texnologiyasini yaratish avtomatlashtirish tizimlarini loyihalashtiruvchilarning asosiy vazifalaridan biri hisoblanadi                                                  3                                                  Fenwick daraxti yoki ikkilik indeksli daraxt (BIT) - bu elementlarni samarali yangilash va raqamlar jadvalidagi prefiks summalarini hisoblash mumkin bo'lgan ma'lumotlar tuzilmasi . Ushbu tuzilma 1989 yilda Boris Ryabko tomonidan taklif qilingan. 1992 yilda nashr etilgan keyingi o'zgartirish bilan. Keyinchalik u 1994 yilgi maqolasida ushbu tuzilmani tasvirlab bergan Piter Fenvik nomidan Fenvik daraxti nomi bilan mashhur bo'ldi . Yassi raqamlar qatori bilan solishtirganda, Fenwick daraxti ikkita operatsiya o'rtasida ancha yaxshi muvozanatga erishadi: elementlarni yangilash va prefiks yig'indisini hisoblash. ning tekis massivi raqamlar elementlarni yoki prefiks summalarini saqlashi mumkin. Birinchi holda, prefiks summalarini hisoblash chiziqli vaqtni talab qiladi; ikkinchi holda, massiv elementlarini yangilash chiziqli vaqtni talab qiladi (har ikkala holatda ham boshqa operatsiya doimiy vaqtda bajarilishi mumkin). Fenwick daraxtlari ikkala operatsiyani ham bajarishga imkon beradi vaqt. Bunga raqamlarn i daraxt shaklida ifodalash orqali erishiladi daraxtdagi har bir tugunning qiymati massivning asosiy (shu jumladan) indeksidan tugun indeksi (eksklyuziv)gacha bo'lgan prefiks yig'indisi bo'lgan tugunlar. Daraxtning o'zi yashirin va massiv sifatida saqlanishi mumkin raqamlar, massivdan yashirin ildiz tugunlari olib tashlangan. Daraxt tuzilishi elementni qidirish, elementni yangilash, prefiks yig'indisi va diapazon yig'indisi operatsiyalarini faqat foydalanishga imkon beradi. Kurs ishining maqsadi: Fenwick daraxti mavzusini o’rganish Kurs ishining tuzilishi : Kurs ish kirish, 2 bob, 5 bo‘lim, umumiy xulosalar va tavsiyalar, foydalanilgan adabiyotlar ro‘yhatidan iborat bo‘lib, jami 22 sahifani tashkil qiladi. 4 I Bob. Daraxt tushunchasi.Daraxtlar grafning xususiy holati. 1.1.Daraxt tushunchasi. Daraxt - bu bog langan asiklik graf, ya’ni sikllar yo q va uchlar juftligi orasidaʻ ʻ bitta yo l bor (29-rasm). Kirishning nol darajasiga ega bo lgan uch daraxtning ildizi, ʻ ʻ chiqish nol darajaga ega tugunlar esa barglar deb nomlanadi. Daraxtlar quyidagi belgilari bilan tavsiflanadi:daraxtda ildiz deb ataluvchi shunday yagona element mavjudki, unga boshqa elementlardan murojaat mavjud emas; daraxt ixtiyoriy elementga murojaat (element qiymatini olish) chekli sondagi ketma-ket murojaatlar yoki ko‘rsatkichlardan o‘tib borish orqali amalga oshiriladi; 1-rasm.Yo’naltirilgan daraxt. Yo naltirilgan (oriyentirlangan) daraxt - bu faqat bitta vertikal kirish nol darajasiga ʻ ega bo lgan (boshqa yoylar unga olib kelmaydigan), boshqa uchlarning kirish ʻ 5 darajasi 1 bo lgan siklik orgraf (sikllarni o z ichiga olmaydigan yo naltirilganʻ ʻ ʻ graf). Daraxtning asosiy tushunchalari . Ildiz tuguni - daraxtning eng yuqori tuguni (2-tugun). Ildiz – ixtiyoriy tanlab olingan uchlardan biri. Barg yoki terminal tuguni – avlodi mavjud bo lmagan tugun. (2,10,5,11,4- ʻ tugunlar) Ichki tugun - bu daraxtga avlodi mavjud bo lgan har qanday tugun .(7,5,9,6- ʻ tugunlar). va shuning uchun barg tuguni emas (18-rasmda 3, 6, 10, 14). Uchning darajasi - unga tushgan qirralarning soni. Daraxt osti - bu alohida daraxt sifatida namoyish etilishi mumkin bo lgan daraxtga o xshash ma’lumotlar strukturasining bir qismidir. T ʻ ʻ daraxtining har qanday tuguni va uning barcha nasl tugunlari bilan birga daraxtining pastki daraxti hisoblanadi. Daraxt osti har qanday tuguni uchun, yo ushbu kichik daraxtning ildiz tuguniga yo l bo lishi kerak, yo ʻ ʻ tugunning o zi ildiz bo lishi kerak. ʻ ʻ Daraxtdagi darajalar soni balandlik deb ataladi. Masalan 1-rasmdagi d araxtning balandligi 3 ga teng. 6 1.2. Tartiblangan va muvozanatlashgan daraxtlar AVL daraxt. AVL-daraxt (inglizcha AVL-Tree) bu muvozanatlashgan ikkilik qidiruv daraxti bo lib, unda quyidagi ʻ xususiyat qo llab-quvvatlanadi: uning har bir uchlari uchun uning ikkita ʻ ostki daraxtining balandligi 1 dan ko p bo lmagan qiymatga farq qiladi. ʻ ʻ AVL daraxtlari birinchi marta 1962-yilda AVL daraxtlaridan foydalanishni taklif qilgan G. M. Adelson-Velskiy va E. M. Landisning ismlarining birinchi harflari bilan nomlangan. Uchlarni muvozanatlash - bu |h(L) − h(R)| = 2 chap va o ng ʻ pastki daraxtlari balandliklari farqi bo lgan taqdirda, |h(L) − h(R)| ≤ 2 daraxtining ʻ xususiyati tiklanishi uchun ushbu uchlarning pastki daraxtidagi ajdod va avlod munosabatlarini o zgartiradigan amal, aks holda hech narsani o zgartirilmaydi. ʻ ʻ Daraxtning balandligi maksimal darajasi, ildizdan tashqi tugunga qadar eng uzun yo lning uzunligi sifatida aniqlanadi. Ikkilik qidiruv daraxti muvozanatli deyiladi, ʻ agar biron bir ugunning chap pastki daraxtining balandligi o ng pastki daraxtning ʻ balandligidan ± 1 dan oshmasa. 7 2-Rasm.AVL DARAXTI AVL daraxtda tugun hosil qilish dasturi. struct avltree *avltree_create(int key,char *value) { struct avltree *node; node = malloc(sizeof(*node)); if (node != NULL) { node->key = key; node->value = value; node->left = NULL; node->right = NULL; node->height = 0; } return node; } 8 Tugundan kalit bo yicha izlash funksiyasi ʻ struct avltree *avltree_lookup(struct avltree *tree, int key) { while(tree !=NULL) { if(key == tree->key) { return tree; } else if(key<tree->key) { tree = tree->left; } else { tree = tree->rigth; } } }; Daraxt strukturasi orasida tartiblangan daraxtlar eng keng tarqalgan. Binar (Ikkilik) qidiruv daraxti - tartiblangan daraxt turidir. Ikkilik daraxt - bu har bir tugunda ko pi bilan ikkita avlod (bola) ʻ bo lgan ma’lumotlarning iyerarxik tuzilishi. Odatda, birinchisi ajdod ʻ tuguni, avlodlar esa chap va o ng merosxo rlar deb nomlanadi. ʻ ʻ 9 2-rasm.Binar(ikkilik daraxt) daraxt. 1.3. Muvozanatlashgan daraxtlar.B daraxt . B daraxti (inglizcha B-tree) – izlash, qo'shish va o'chirish imkonini beradigan, juda ko pshoxli muvozanatlashgan qidiruv daraxti. Tugunlari ʻ n bo'lgan B daraxti O(logn) balandlikka ega bo‘ladi. Tugun shoxlari soni bittadan bir necha minggacha bo'lishi mumkin (odatda, B-daraxtining shoxlanish darajasi daraxt ishlaydigan qurilma (disklar) xususiyatlari bilan belgilanadi). B-daraxtlar O(logn) ko'p dinamik to'plam amallarini o'z vaqtida bajarish uchun ham ishlatilishi mumkin. B daraxti birinchi marta 1970-yilda R. Bayer va E. Makkreyt tomonidan taklif qilingan. B daraxt strukturasi. B daraxti mukammal muvozanatlashgan ya'ni uning barcha barglarining chuqurligi bir xil. B daraxti quyidagi xususiyatlarga ega ( t – bu daraxt parametrlari, B daraxtining minimal darajasi deyiladi, 2 dan kam emas ): Ildizdan tashqari har bir tugun hech bo'lmaganda t-1 kalitni o'z 10 ichiga oladi va har bir ichki tugun kamida avlodli t tugunlarga ega. Agar daraxt bo'sh bo'lmasa, ildizda kamida bitta kalit bo'lishi kerak. Har bir tugunning kalitlari kamaymaydigan tartibda tartiblangan. Barcha barglar bir xil darajada. 3-RASM. B DARAXT. B daraxtni hosil qilish. 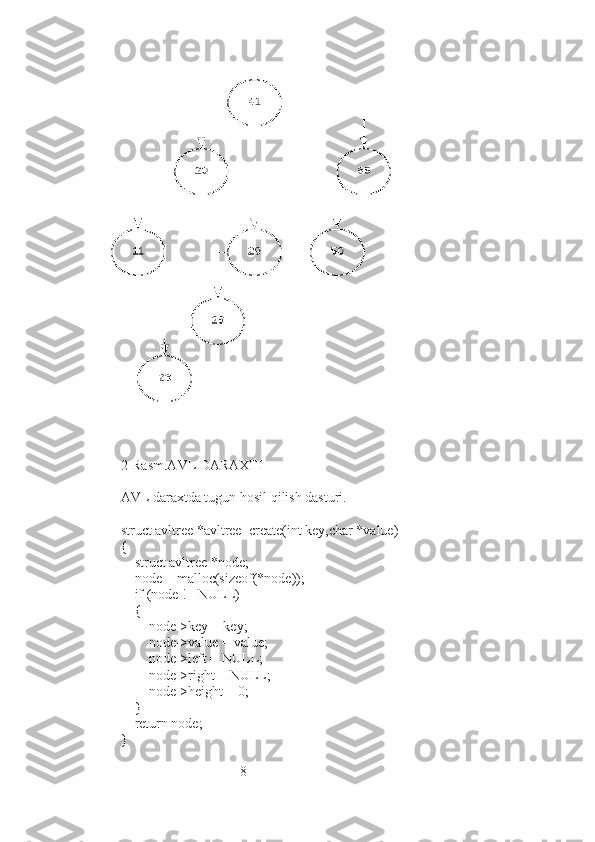struct btree *btree_create() { struct btree *node; node = malloc(sizeof(*node)); node->leaf = 1; node->nkeys = 0; node->key = malloc(sizeof(*node->key) * 2 * T - 1); node->value = malloc(sizeof(*node->value) 2 * T - 1); node->child = malloc(sizeof(*node->child) 2 * T); 11 return node; } B daraxtda element izlash void btree_lookup(struct btree *tree, int key, struct btree **node, int *index) { int i; for (i = 0; i < tree->nkeys && key > tree->key[i]; ) { i++; } if (i < tree->nkeys && key == tree->key[i]) { *node = tree; *index = i; return; } if (!tree->leaf) { /* Disk read tree->child[i] */ btree_lookup(tree, key, node, index); } else { *node = NULL; } 12 II.BOB. DARAXTNING STRUKTURALARI VA DASTURI. 2.1. Fenwick daraxti. Fenwick daraxti   yoki   ikkilik   indeksli daraxt   (BIT)   - bu elementlarni samarali yangilash va raqamlar jadvalidagi   prefiks summalarini   hisoblash mumkin bo'lgan ma'lumotlar tuzilmasi . Ushbu tuzilma 1989 yilda Boris Ryabko tomonidan taklif qilingan.   1992 yilda nashr etilgan keyingi o'zgartirish bilan.   Keyinchalik u 1994 yilgi maqolasida ushbu tuzilmani tasvirlab bergan   Piter Fenvik   nomidan Fenvik daraxti nomi bilan mashhur bo'ldi .   Yassi raqamlar qatori bilan solishtirganda, Fenwick daraxti ikkita operatsiya o'rtasida ancha yaxshi muvozanatga erishadi: elementlarni yangilash va prefiks yig'indisini hisoblash.   ning tekis massivi raqamlar elementlarni yoki prefiks summalarini saqlashi mumkin.   Birinchi holda, prefiks summalarini hisoblash chiziqli vaqtni talab qiladi;   ikkinchi holda, massiv elementlarini yangilash chiziqli vaqtni talab qiladi (har ikkala holatda ham boshqa operatsiya doimiy vaqtda bajarilishi mumkin).   Fenwick daraxtlari ikkala operatsiyani ham bajarishga imkon beradi vaqt.   Bunga raqamlarni   daraxt   shaklida ifodalash orqali erishiladi daraxtdagi har bir tugunning qiymati massivning asosiy (shu jumladan) indeksidan tugun indeksi (eksklyuziv)gacha bo'lgan prefiks yig'indisi bo'lgan tugunlar.   Daraxtning o'zi yashirin va massiv sifatida saqlanishi mumkin raqamlar, massivdan yashirin ildiz tugunlari olib tashlangan.   Daraxt tuzilishi elementni qidirish, elementni yangilash, prefiks yig'indisi va diapazon yig'indisi operatsiyalarini faqat foydalanishga imkon beradi. 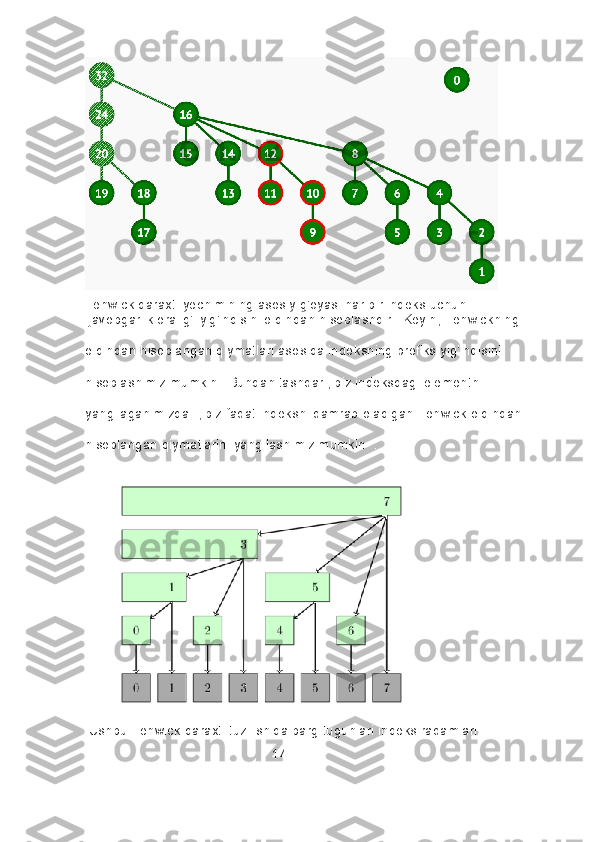13 Fenwick daraxti yechimining asosiy g'oyasi har bir indeks uchun javobgarlik oralig'i yig'indisini oldindan hisoblashdir. Keyin, Fenwickning oldindan hisoblangan qiymatlari asosida indeksning prefiks yig'indisini hisoblashimiz mumkin . Bundan tashqari, biz indeksdagi elementni yangilaganimizda , biz faqat indeksni qamrab oladigan Fenwick oldindan hisoblangan qiymatlarini yangilashimiz mumkin . Ushbu Fenwick daraxti tuzilishida barg tugunlari indeks raqamlari 14 hisoblanadi. Har bir ichki tugun Fenwick qiymatini o'z ichiga oladi, uni o'z farzandlari Fenwick qiymatlari va o'zining indeks qator raqamidan tuzish mumkin. Fenwick daraxti, shuningdek, Binary Indexed Tree deb ataladi yoki shunchaki BIT qisqartiriladi. Fenwick Tree deb ham ataladigan ikkilik indeksli daraxt massivdagi samarali hisoblash imkonini beradi. Masalan, massiv [2, 3, -1, 0, 6] uzunlikdagi 3 prefiksi [2, 3, -1] yig'indisi 2 + 3 + -1 = 4). Prefiks summalarini samarali hisoblash turli stsenariylarda foydalidir. Keling, oddiy muammodan boshlaylik.Bizga a[] massivi berilgan va biz u bilan ikki turdagi amallarni bajara olishni xohlaymiz.i indeksida saqlangan qiymatni o'zgartiring. (Bu nuqta yangilash operatsiyasi deb ataladi ) 1.Uzunligi k bo‘lgan prefiksning yig‘indisini toping. (Bu diapazon yig'indisi so'rovi deb ataladi ) Yuqoridagilarning to'g'ridan-to'g'ri amalga oshirilishi shunday ko'rinadi . int a [] = { 2 , 1 , 4 , 6 , - 1 , 5 , - 32 , 0 , 1 }; void update ( int i , int v ) { a [ i ] = v ; } int prefixsum ( int k ) { int sum = 0 ; for ( int i = 0 ; i < k ; i ++) sum += a [ i ]; return sum ; } Bu mukammal yechim, lekin afsuski, prefiks yig'indisini hisoblash uchun zarur bo'lgan vaqt massiv uzunligiga mutanosibdir, shuning uchun ko'p sonli aralashgan operatsiyalar bajarilganda bu vaqt tugaydi. 15 Bundan yaxshiroq ish qila olamizmi? Albatta. Samarali yechimlardan biri O(logN) vaqtida ikkala operatsiyani ham bajara oladigan segment daraxtidan foydalanishdir. Ikkilik indekslangan daraxtdan ham foydalanib, biz ikkala vazifani O(logN) vaqtida bajarishimiz mumkin. 2.2. Fenwick daraxti dasturiy tahlili. Ikkilik indeksli daraxtni tushunish uchun quyidagi masalani ko'rib chiqaylik. Bizdaarr[0massivibor. . . n-1]. Biz 1 Birinchi i elementlarning yig'indisini hisoblamoqchimiz . 2 arr[i] = x massivning belgilangan elementining qiymatini o'zgartiring, bu erda 0 <= i <= n-1. Oddiy yechim 0 dan i-1 gacha bo'lgan tsiklni bajarish va elementlarning yig'indisini hisoblashdir. Qiymatni yangilash uchun arr[i] = x ni bajaring. Birinchi operatsiya O(n) vaqtni oladi, ikkinchi operatsiya esa O(1) vaqtni oladi. Yana bir oddiy yechim qo‘shimcha massiv yaratish va bu yangi massivda i-indeksdagi birinchi i-chi elementlarning yig‘indisini saqlashdir. Berilgan diapazonning yig'indisi endi O(1) vaqt ichida hisoblanishi mumkin, ammo yangilash jarayoni hozir O(n) vaqtni oladi. Agar so'rov operatsiyalari ko'p bo'lsa, lekin yangilash operatsiyalari juda oz bo'lsa, bu yaxshi ishlaydi. O (log n) vaqtida so'rov va yangilash operatsiyalarini bajara olamizmi? S amarali yechimlardan biri O(Logn) vaqtida ikkala operatsiyani bajaradigan SegmentTree-dan foydalanishdir . Muqobil yechim ikkilik indeksli daraxt bo'lib, u ikkala operatsiya uchun ham O(Logn) vaqt murakkabligiga erishadi. Segment daraxti bilan solishtirganda, Binary Indexed Tree kamroq joy talab qiladi va amalga oshirish osonroq. Binary Indexed Tree massiv sifatida taqdim etiladi. Massiv BITree[] bo‘lsin. Ikkilik indeksli daraxtning har bir tugunida kirish massivining ba'zi elementlari yig'indisi saqlanadi. Ikkilik indeksli daraxtning o'lchami kirish massivining o'lchamiga teng 16 bo'lib, n bilan belgilanadi. Quyidagi kodda biz amalga oshirish qulayligi uchun n+1 o'lchamidan foydalanamiz. Bu g‘oya barcha musbat sonlarni 2 ning darajalari yig‘indisi sifatida ifodalash mumkinligiga asoslanadi. Masalan, 19 ni 16 + 2 + 1 sifatida ko‘rsatish mumkin. BITree ning har bir tugunida n ta element yig‘indisi saqlanadi. 2 ning kuchi. Masalan, yuqoridagi birinchi diagrammada (getSum() diagrammasi) dastlabki 12 ta elementning yig‘indisi oxirgi 4 ta elementning yig‘indisi (9 dan 12 gacha) va 8 ning yig‘indisi bilan olinishi mumkin. elementlar (1 dan 8 gacha). n sonining ikkilik ko'rinishidagi o'rnatilgan bitlar soni O(Logn) dir. Shuning uchun biz getSum() va update() operatsiyalarida eng ko'p O(Logn) tugunlarini kesib o'tamiz. Qurilishning vaqt murakkabligi O(nLogn) dir, chunki u barcha n element uchun update() ni chaqiradi. // Ikkilik indeks daraxtining amallarini ko'rsatish uchun C++ kod #include <iostream> using namespace std; { int sum = 0; index = index + 1; while (index>0) { sum += BITree[index]; index -= index & (-index); } return sum; } void updateBIT(int BITree[], int n, int index, int val){ index = index + 1; while (index <= n) { BITree[index] += val; index += index & (-index); 17 } } int *constructBITree(int arr[], int n) { int *BITree = new int[n+1]; for (int i=1; i<=n; i++) BITree[i] = 0; for (int i=0; i<n; i++) updateBIT(BITree, n, i, arr[i]); for (int i=1; i<=n; i++) cout << BITree[i] << " "; return BITree; } int main() { int A[] = {2, 1, 1, 3, 2, 3, 4, 5, 6, 7, 8, 9}; int n = sizeof(A)/sizeof(A[0]); int *BITree = constructBITree(A, n); cout << "Sum of elements in arr[0..5] is " << getSum(BITree, 5); A[3] += 6; updateBIT(BITree, n, 3, 6); cout << "\nYangilanishdan keyin arr[0..5] dagi elementlar yig indisi "ʻ << getSum(BITree, 5); return 0;} Ikkilik indeksli daraxt (Fenwick Tree)   massivning prefiks yig'indisini   tezda hisoblash   uchun ishlatilishi mumkin bo'lgan   samarali ma'lumotlar strukturasidir. Agar massivda mavjud qiymatlar o'zgaruvchan bo'lsa . m   .   e   . qiymatlarni Fenwick daraxti   yordamida o'zgartirish mumkin,   bu juda foydali. Odatda, agar biz 18 Ikkilik indeksli daraxt (Fenwick Tree)   massivning prefiks yig'indisini   tezda hisoblash   uchun ishlatilishi mumkin bo'lgan   samarali ma'lumotlar strukturasidir. Agar massivda mavjud qiymatlar o'zgaruvchan bo'lsa . m   .   e   . qiymatlarni Fenwick daraxti   yordamida o'zgartirish mumkin,   bu juda foydali. Odatda, agar biz massivdagi 0 dan n gacha bo'lgan barcha raqamlarning yig'indisini hisoblamoqchi bo'lsak, biz indeks-0 dan boshlab har bir elementni ko'rib chiqamiz va indeks-n ga qadar barcha elementlarni qo'shishni davom ettiramiz.   Bu O(n) vaqtini oladi va o'lcham juda katta bo'lsa va biz ko'p so'rovlarni bajarishimiz kerak bo'lganda samarali emas.Buning bir yechimi prefiks sum massividan foydalanishdir.   Prefiks yig'indisi massivi oldindan hisoblangan massiv bo'lib, unda har qanday indeksdagi qiymat asl massivdagi 0 dan ushbu indeksgacha bo'lgan barcha raqamlar yig'indisiga teng bo'ladi.   Agar bizdan x va y o'rtasidagi indekslarning umumiy yig'indisini olishni so'ragan so'rovni olsak, biz x-1 indeksidagi prefiks summasini y indeksidagi prefiks yig'indisidan ayirishimiz kerak, bu bizga x indekslaridagi elementlarning yig'indisini beradi. y ga.   Bu faqat 2 ta operatsiyani oladi va shuning uchun biz O (1) vaqtida diapazon summasini olishimiz mumkin.   Ammo diqqatga sazovor narsa shundaki, agar indeksdagi qiymat   i o'zgarsa, kattaroq indekslar uchun barcha prefiks summalari   i o'zgaradi va bu O(N) vaqtini oladi.Xulosa qilib aytadigan bo'lsak, birinchi yondashuv   O(N) har qanday berilgan indekslar orasidagi barcha elementlarning yig'indisini hisoblash uchun vaqt talab etadi, ammo   O(1) har qanday elementni yangilash uchun vaqt kerak bo'ladi.   Prefiks yig'indisidan foydalangan holda ikkinchi yondashuvda,   O(1) har qanday berilgan indekslar orasidagi barcha elementlarning yig'indisini hisoblash uchun vaqt kerak bo'ladi, lekin   O(N) agar dastlabki massivdagi biron bir element o'zgargan bo'lsa, prefiks yig'indisi qatorini yangilash uchun vaqt kerak bo'ladi.Endi savol shundaki, ikkalamiz o'rtasida muvozanat bo'lishi mumkinmi?   ya'ni, har qanday elementni yangilash vaqtida o'rtacha vaqt murakkabligi va prefiks summalarini hisoblash uchun o'rtacha vaqt murakkabligi bormi?   Ikkilik indeksli daraxt yoki Fenwick daraxti bu savolning bir yechimidir . 19 ADABIYOTLAR RO’YXATI 1.Misty E Vermaat, Susan L Sebok, Steven M Freund. Discovering Computers (C)2016 (2016 edition). Textbook.USA, 2016. 2.Mamarajabov M., Tursunov S. Kompyuter grafikasi va Web dizayn: Darslik. T.: Cho‘lpon, 2013. 3.A.A. Xoidjigitov , Sh.f.Madraximov, U.E.Adamboyev “Informatika va programmalash ” .O`quv qo`llanma, O`z.MU . 2005-yil. 4..B. Straustrop. “Yazik programmirovaniya C++. ” Binom press, 2006-yil. 5. Boltayev B.J , Azamatov A.R , Rahimov A.D “Algoritmlash va dasturlash asoslari” kitobi 6.A.M. Po’latov “Algoritmlash va C++ dasturlash asoslari” kitobi 7. A.R. Azamatov “Algoritmlash asoslari” kitobi 1. https://library.ziyonet.uz/uz/book/126181 https://library.ziyonet.uz/uz/book/index?Book%5Blevel_id%5D=&Book %5Btype_id%5D=1&Book%5Bcategory_id%5D=53&Book%5Btitle %5D=&Book%5Bdescription%5D=&Book%5Blanguage_id%5D=&yt0=Qidiruv 20 ILOVALAR ILOVA 1. Modul N1 boshlang’ich kodi. class FenwickTree { private : //xususiy vector < int > data; //vector e’lon qilinyabdi int getParent ( int i) const {// return i - (i & ( - i)); //qiymatini qaytarayabdi } int getNext ( int i) const { return i + (i & ( - i)); //qiymatini qaytarayabdi } public : //dasturning ixtiyoriy joyida ishlaydi FenwickTree( int n) : data(n +1 , 0 ) { } int getSum( int i) const { int sum = 0 ;//s=0 deb uzgaruvchi olayabmiz ++ i; while (i > 0 ) { sum += data[i]; i = getParent(i); } return sum; } void update( int i, int v) { ++ i; while (i < data.size()) {// massiv o’lchamini olish data[i] += v; i = getNext(i); } } }; 21

Mavzu: “Fenwick daraxti” MUNDARIJA KIRISH ........................................................................................................... 3 1.1.Daraxt tushunchasi. ............................................................................. 5 B daraxtda element izlash .............................................................................. 13 void btree_lookup(struct btree *tree, int key, ................................................ 13 struct btree **node, int *index) ..................................................................... 13 { ..................................................................................................................... 13 int i; ................................................................................................................ 13 for (i = 0; i < tree->nkeys && key > tree->key[i]; ) { ................................... 13 i++; ................................................................................................................ 13 } ..................................................................................................................... 13 if (i < tree->nkeys && key == tree->key[i]) { .............................................. 13 *node = tree; .................................................................................................. 13 *index = i; ...................................................................................................... 13 return; ............................................................................................................ 13 } ..................................................................................................................... 13 if (!tree->leaf) { ............................................................................................. 13 /* Disk read tree->child[i] */ ......................................................................... 13 btree_lookup(tree, key, node, index); ............................................................ 13 } else { ........................................................................................................... 13 *node = NULL; } .......................................................................................... 13 II.BOB. DARAXTNING STRUKTURALARI VA DASTURI. .................. 14 2.2. Fenwick daraxti dasturiy tahlili. ....................................................... 17 Ikkilik indeksli daraxt (Fenwick Tree) massivning prefiks yig'indisini tezda hisoblash uchun ishlatilishi mumkin bo'lgan samarali ma'lumotlar strukturasidir.Agar massivda mavjud qiymatlar o'zgaruvchan bo'lsa. m   . e   .qiymatlarni Fenwick daraxti yordamida o'zgartirish mumkin, bu juda foydali.Odatda, agar biz massivdagi 0 dan n gacha bo'lgan barcha raqamlarning yig'indisini hisoblamoqchi bo'lsak, biz indeks-0 dan boshlab har bir elementni ko'rib chiqamiz va indeks-n ga qadar barcha elementlarni qo'shishni davom ettiramiz. Bu O(n) vaqtini oladi va o'lcham juda katta bo'lsa va biz ko'p so'rovlarni bajarishimiz kerak bo'lganda samarali emas.Buning bir yechimi prefiks sum massividan foydalanishdir. Prefiks yig'indisi massivi oldindan hisoblangan massiv bo'lib, unda har qanday indeksdagi qiymat asl massivdagi 0 dan ushbu indeksgacha bo'lgan barcha raqamlar yig'indisiga teng bo'ladi. Agar bizdan x va y o'rtasidagi indekslarning umumiy yig'indisini olishni so'ragan so'rovni olsak, biz x-1 indeksidagi prefiks summasini y indeksidagi prefiks yig'indisidan ayirishimiz kerak, bu bizga x indekslaridagi elementlarning yig'indisini beradi. y ga. Bu faqat 2 ta operatsiyani oladi va shuning uchun biz O (1) vaqtida diapazon summasini

olishimiz mumkin. Ammo diqqatga sazovor narsa shundaki, agar indeksdagi qiymat io'zgarsa, kattaroq indekslar uchun barcha prefiks summalari io'zgaradi va bu O(N) vaqtini oladi.Xulosa qilib aytadigan bo'lsak, birinchi yondashuv O(N)har qanday berilgan indekslar orasidagi barcha elementlarning yig'indisini hisoblash uchun vaqt talab etadi, ammo O(1)har qanday elementni yangilash uchun vaqt kerak bo'ladi. Prefiks yig'indisidan foydalangan holda ikkinchi yondashuvda, O(1)har qanday berilgan indekslar orasidagi barcha elementlarning yig'indisini hisoblash uchun vaqt kerak bo'ladi, lekin O(N)agar dastlabki massivdagi biron bir element o'zgargan bo'lsa, prefiks yig'indisi qatorini yangilash uchun vaqt kerak bo'ladi.Endi savol shundaki, ikkalamiz o'rtasida muvozanat bo'lishi mumkinmi? ya'ni, har qanday elementni yangilash vaqtida o'rtacha vaqt murakkabligi va prefiks summalarini hisoblash uchun o'rtacha vaqt murakkabligi bormi? Ikkilik indeksli daraxt yoki Fenwick daraxti bu savolning bir yechimidir. 21 ADABIYOTLAR RO’YXATI ...................................................................... 22 ILOVALAR ................................................................................................... 23 ILOVA 1. Modul N1 boshlang’ich kodi. ............................................... 23

KIRISH Mavzuning dolzarbligi . Bugungi kunda ma‘lumotlar oqimining ko‘pligi tufayli ularni qisqa vaqt ichida qayta ishlash muommosi ham ortib bormoqda. Hozirgi vaqtda axborot- kommunikasiya vositalari barcha turdagi tashkilot va muassasalarga shiddat bilan kirib kelmoqda. Axborotlarning haddan tashqari ko‘pligi bu axborotlarni saqlashda, qayta ishlashda, hamda har xil turdagi tizimlarni yaratish, ulardan keng foydalanishni va axborot tizimlari yaratishni talab qiladi. O‘zbekiston Respublikasi Prezidentining 2017 yil 7 fevraldagi PF-4947-son Farmoni bilan tasdiqlangan 2017-2021 yillarda O‘zbekiston Respublikasini rivojlantirishning beshta ustuvor yo‘nalishi bo‘yicha harakatlar strategiyasi mamlakatning davlat va jamiyat rivojlanishi istiqbolini strategik rejalashtirish tizimiga sifat jihatdan yangi yondashuvlarni boshlab berdi[1]. Unda belgilangan vazifalar sirasida ta‘lim va fan sohasini rivojlantirish ham aloxida ko‘zda tutilgan. O‘zbekiston Respublikasi birinchi Prezidentining 2012 yil 21 martdagi “Zamonaviy axborot-kommunikasiya texnologiyalarini yanada joriy etish va rivojlantirish chora-tadbirlari to‘g‘risida”gi PQ-1730 Qarori hamda “O‘zbekiston Respublikasida —Elektron ta‘lim milliy tarmog‘ini yaratish” investision loyihasini amalga oshirish chora-tadbirlari to‘g‘risida” gi PQ-1740 Qarori va me‘yoriy hujjatlar asosida algoritmik ta‘minot ishlab chiqish va joriy etish keng ko‘lamli hisoblanadi. Barcha tashkilot va muassasalarda avtomatlashtirilgan tizimlar yaratish ulardan keng ko‘lamda foydalanish uchun algoritmlash tillarini o‘rni katta hisoblanadi. Axborot tizimlari axborotni to‘plash, saqlash va qayta ishlash uchun, keng imkoniyatli maqsadlarda samarali foydalanish uchun xizmat qiladi. Zamonaviy axborotlashtirish tizimi, ma‘lumotlar integratsiyasi konsepsiyasiga asoslangan katta hajmdagi ma‘lumotlarni saqlash bilan tavsiflanadi va ko‘p sondagi foydalanuvchilarning turli xildagi talablariga javob berishi kerak bo‘ladi. Axborot tizimi va axborot texnologiyalarining avtomatlashtirilgan elementlarini qo‘llash va avtomatlashtirish asosida yangi axborot texnologiyasini yaratish avtomatlashtirish tizimlarini loyihalashtiruvchilarning asosiy vazifalaridan biri hisoblanadi   

                                              3                                                  Fenwick daraxti yoki ikkilik indeksli daraxt (BIT) - bu elementlarni samarali yangilash va raqamlar jadvalidagi prefiks summalarini hisoblash mumkin bo'lgan ma'lumotlar tuzilmasi . Ushbu tuzilma 1989 yilda Boris Ryabko tomonidan taklif qilingan. 1992 yilda nashr etilgan keyingi o'zgartirish bilan. Keyinchalik u 1994 yilgi maqolasida ushbu tuzilmani tasvirlab bergan Piter Fenvik nomidan Fenvik daraxti nomi bilan mashhur bo'ldi . Yassi raqamlar qatori bilan solishtirganda, Fenwick daraxti ikkita operatsiya o'rtasida ancha yaxshi muvozanatga erishadi: elementlarni yangilash va prefiks yig'indisini hisoblash. ning tekis massivi raqamlar elementlarni yoki prefiks summalarini saqlashi mumkin. Birinchi holda, prefiks summalarini hisoblash chiziqli vaqtni talab qiladi; ikkinchi holda, massiv elementlarini yangilash chiziqli vaqtni talab qiladi (har ikkala holatda ham boshqa operatsiya doimiy vaqtda bajarilishi mumkin). Fenwick daraxtlari ikkala operatsiyani ham bajarishga imkon beradi vaqt. Bunga raqamlarn i daraxt shaklida ifodalash orqali erishiladi daraxtdagi har bir tugunning qiymati massivning asosiy (shu jumladan) indeksidan tugun indeksi (eksklyuziv)gacha bo'lgan prefiks yig'indisi bo'lgan tugunlar. Daraxtning o'zi yashirin va massiv sifatida saqlanishi mumkin raqamlar, massivdan yashirin ildiz tugunlari olib tashlangan. Daraxt tuzilishi elementni qidirish, elementni yangilash, prefiks yig'indisi va diapazon yig'indisi operatsiyalarini faqat foydalanishga imkon beradi. Kurs ishining maqsadi: Fenwick daraxti mavzusini o’rganish Kurs ishining tuzilishi : Kurs ish kirish, 2 bob, 5 bo‘lim, umumiy xulosalar va tavsiyalar, foydalanilgan adabiyotlar ro‘yhatidan iborat bo‘lib, jami 22 sahifani tashkil qiladi. 4

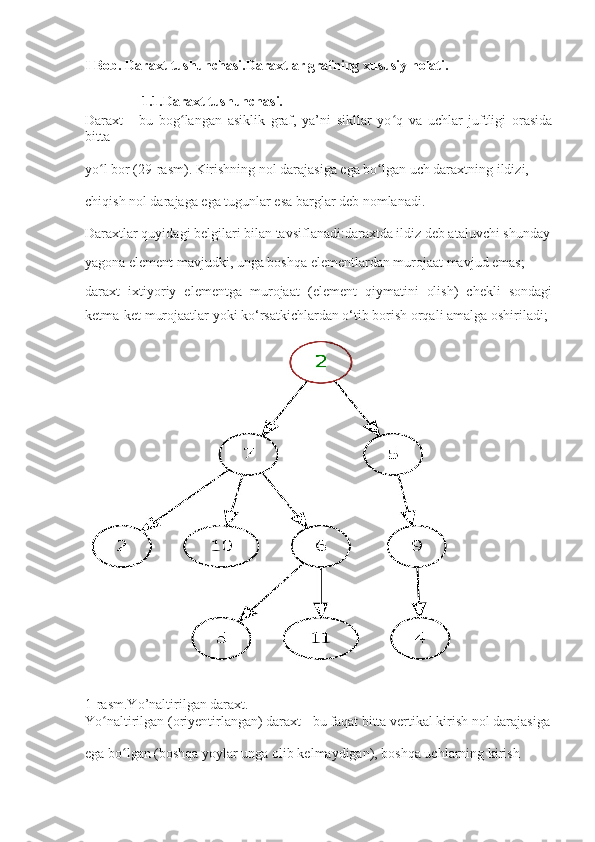
I Bob. Daraxt tushunchasi.Daraxtlar grafning xususiy holati. 1.1.Daraxt tushunchasi. Daraxt - bu bog langan asiklik graf, ya’ni sikllar yo q va uchlar juftligi orasidaʻ ʻ bitta yo l bor (29-rasm). Kirishning nol darajasiga ega bo lgan uch daraxtning ildizi, ʻ ʻ chiqish nol darajaga ega tugunlar esa barglar deb nomlanadi. Daraxtlar quyidagi belgilari bilan tavsiflanadi:daraxtda ildiz deb ataluvchi shunday yagona element mavjudki, unga boshqa elementlardan murojaat mavjud emas; daraxt ixtiyoriy elementga murojaat (element qiymatini olish) chekli sondagi ketma-ket murojaatlar yoki ko‘rsatkichlardan o‘tib borish orqali amalga oshiriladi; 1-rasm.Yo’naltirilgan daraxt. Yo naltirilgan (oriyentirlangan) daraxt - bu faqat bitta vertikal kirish nol darajasiga ʻ ega bo lgan (boshqa yoylar unga olib kelmaydigan), boshqa uchlarning kirish ʻ

O'xshashlar

Fenvik daraxti
Ikkkilik qidruv daraxti
Fenvik daraxti va algoritmi
DEKART DARAXTI (TREAP, DERAMID)
Lindonning dekompozisiyasi. Duval algoritimi