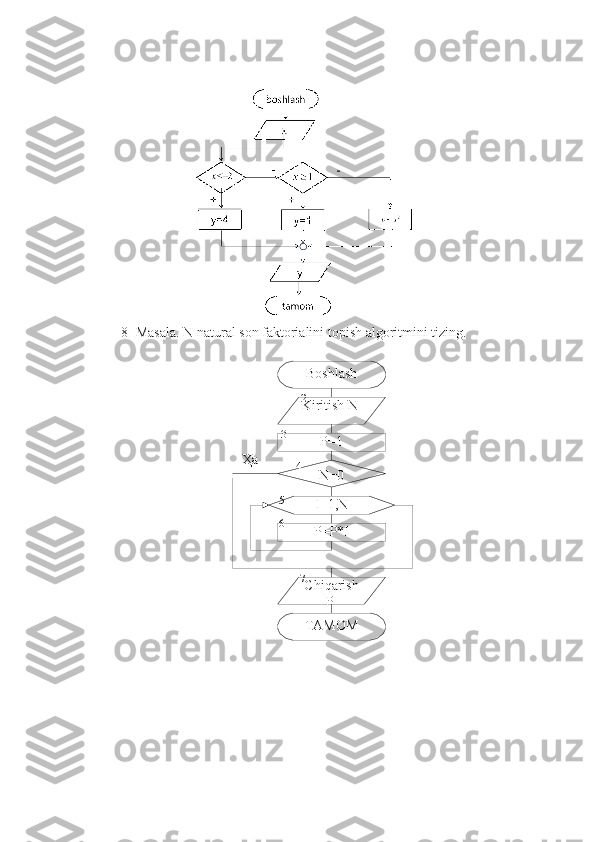
Algoritm turlari 1. Chiziqli strukturali algoritmlar 2. Tarmoqli strukturali algoritmlar 3. Siklik strukturali algoritmlar

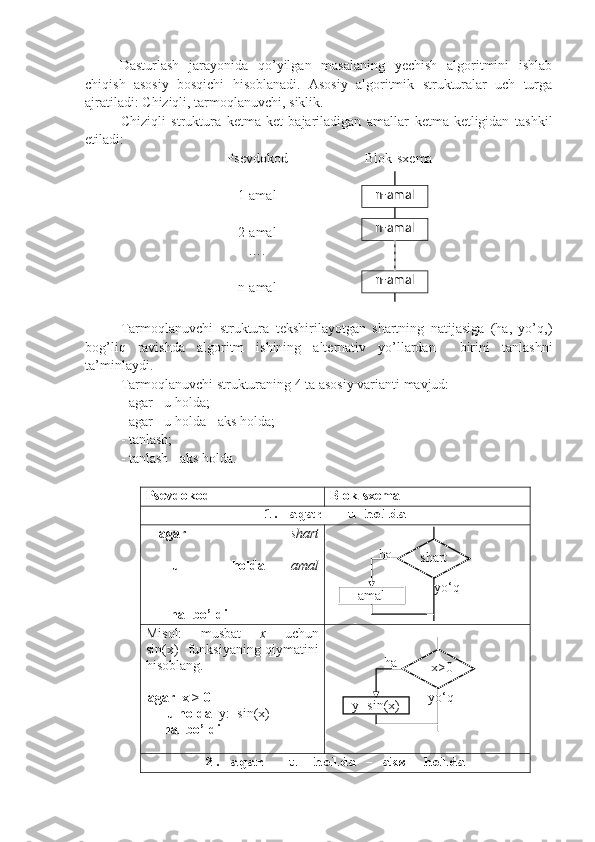
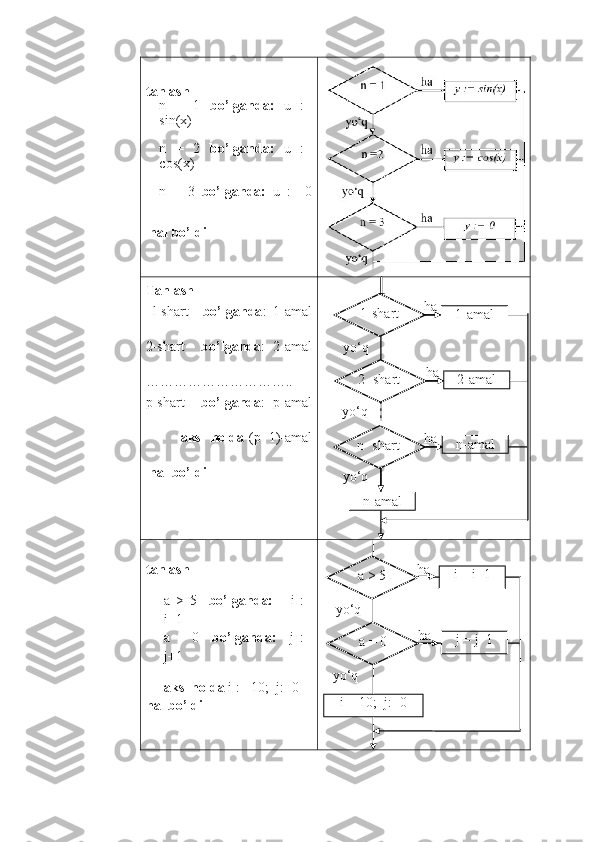
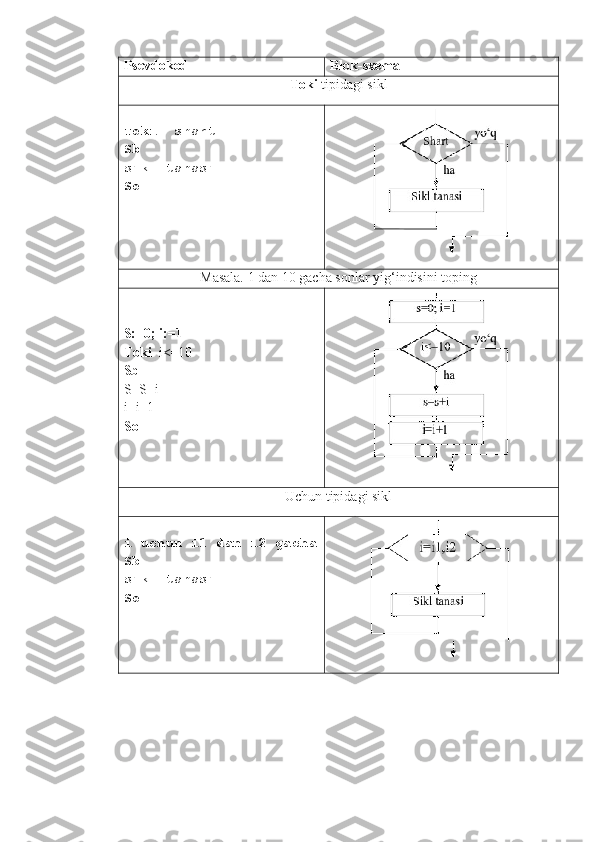
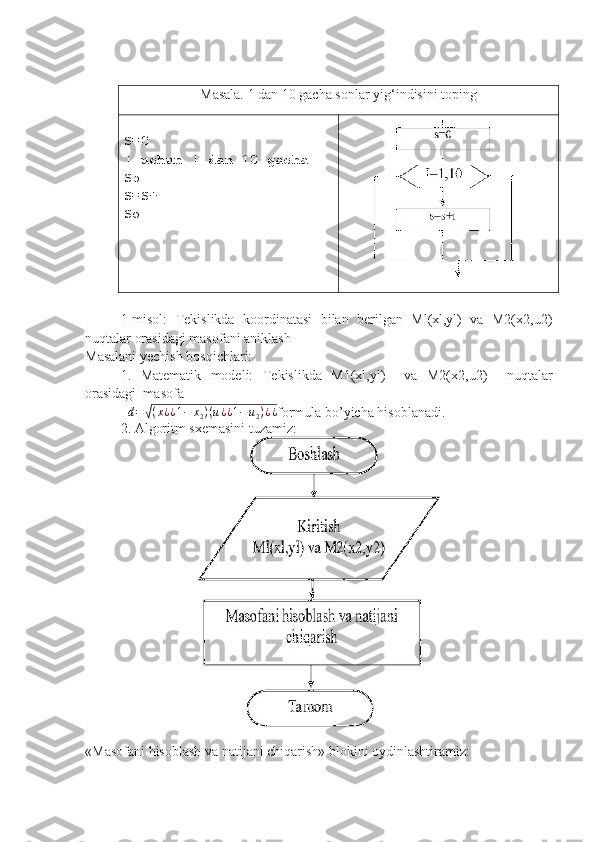
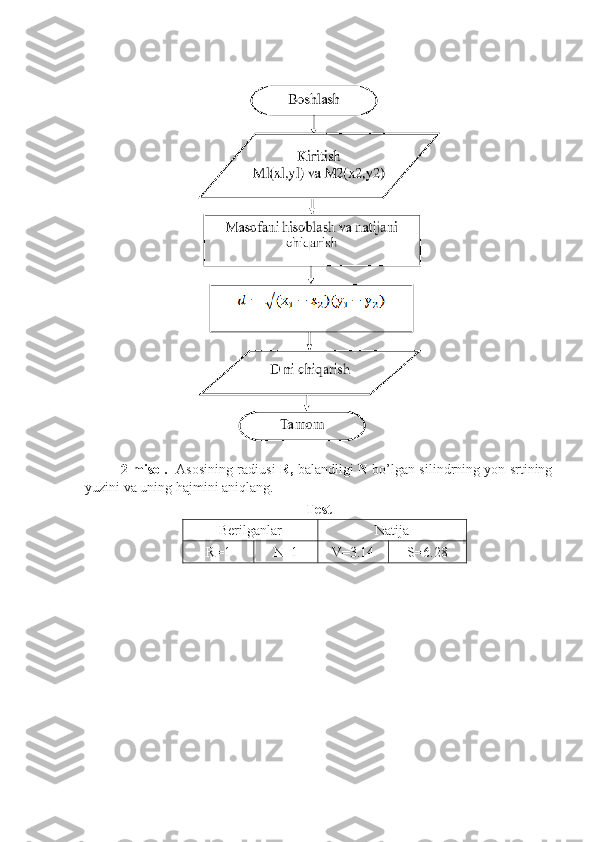
Dasturlash jarayonida qo’yilgan masalaning yechish algoritmini ishlab chiqish asosiy bosqichi hisoblanadi. Asosiy algoritmik strukturalar uch turga ajratiladi: Chiziqli, tarmoqlanuvchi, siklik. Chiziqli struktura ketma-ket bajariladigan amallar ketma-ketligidan tashkil etiladi: Psevdokod Blok-sxema 1-amal 2 -amal …. n -amal Tarmoqlanuvchi struktura tekshirilayotgan shartning natijasiga (ha, yo’q,) bog’liq ravishda algoritm ishining alternativ yo’llardan birini tanlashni ta’minlaydi. Tarmoqlanuvchi strukturaning 4 ta asosiy varianti mavjud: - agar - u holda; - agar - u holda - aks holda; - tanlash; - tanlash - aks holda. Psevdokod Blok-sxema 1. agar - u holda agar shart u holda amal hal bo’ldi Misol: musbat x uchun sin(x) funksiyaning qiymatini hisoblang. agar x > 0 u holda y:=sin(x) hal bo’ldi 2. agar - u holda - aks holda n-amaln-amal n-amal yo‘qha shart amal yo‘qha х>0 y=sin(x)

Agar shart u holda 1-amal aks holda 2-amal hal bo’ldi Masala. Ikkita a, b sonlar berilgan. Agar birinchi son ikkinchi sondan katta bo’lsa, u holda uni ikkilantiring, ikkinchi sonni bir soni bilan almashtiring, aks holda birinchi sonni o’zgarishsiz qoldiring, ikkinchi sonni esa ikkilantiring. agar a>b u holda a:= 2*a; b= 1 aks holda b= 2*b hal bo’ldi 3. tanlash Tanlash 1-shart bo’lganda: 1-amal 2-shart bo’lganda: 2- amal …………………………… n-shart bo’lganda: n-amal hal bo’ldi Masala . Natural son n qiymatiga bog ’ liq ravishda , 1, 2 yoki 3 qiymatlar qabul qilganda , mos ravishda u ga sinx , cosx yoki nol kiymatlarni ta ’ minlang . yo‘q ha Shart 1- amal 2-amal yo‘q ha a>b а = 2*а; b= 1 b= 2*b

tanlash n = 1 bo’lganda: u := sin(x) n = 2 bo’lganda: u := cos(x) n = 3 bo’lganda: u := 0 hal bo’ldi Tanlash l-shart bo’lganda : 1-amal 2-shart bo’lganda : 2-amal ………………………….. p-shart bo’lganda : p-amal aks holda (p+1)-amal hal bo’ldi tanlash a > 5 bo’lganda: i := i+1 a = 0 bo’lganda: j := j +1 aks holda i := 10; j:=0 hal bo’ldi yo‘q yo‘q ha ha ha 1-amal yo‘q 1- shart n- shart 2- shart 2- amal n-amal n-amal yo‘q haha i = i+1 yo‘q а > 5 а = 0 j = j+1 i = 10; j:=0

Siklik struktura sikl tanasi deb nomlanuvchi qandaydir amallar to’plamini bir necha takror bajarilishini ta’minlaydi. Sikllarni asosiy ko’rinishlari jadvalda keltirilgan.