Fazoda to`g`ri chiziqning normal tenglamalari





Fazoda to`g`ri chiziqning normal tenglamalari.
Tekislik va uning tenglamalari • Fazoda ikki nuqta berilgan bo’lsin. Bu nuqtalardan bir xil masofada turgan nuqtalar to’plami (nuqtalarning geometrik o’rni) tekislik deb qaraladi.
• Te kislikning fazodagi o’rnini uning koordinatalar boshqacha bo’lgan masofasi p ya’ni O nuqtadan unga o’tkazilgan OP perpendikulyarning uzunligi bilan, hamda O dan tekislik tomon yo’nalgan birlik vektor bilan aniqlash mumkin. p M O np n 0 o n n r M O np 0
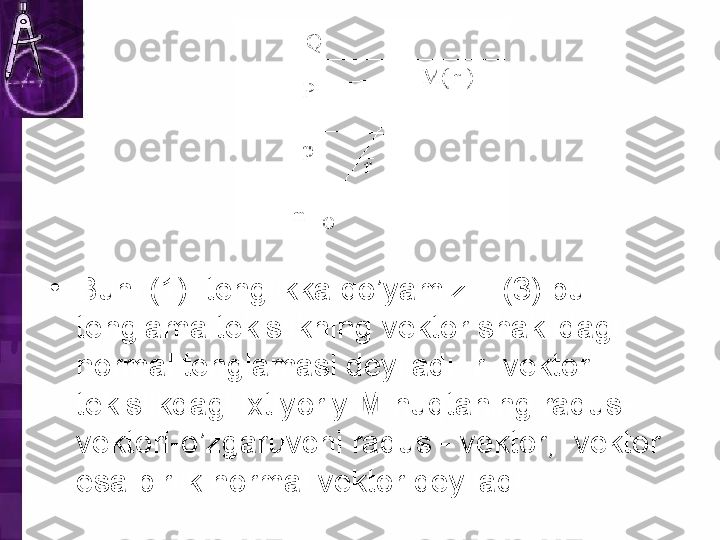
• Buni (1) tenglikka qo’yamiz. (3) bu tenglama tekislikning vektor shaklidagi normal tenglamasi deyiladi. r vektor tekislikdagi ixtiyoriy M nuqtaning radus- vektori-o’zgaruvchi radus - vektor, vektor esa birlik normal vektor deyiladi.
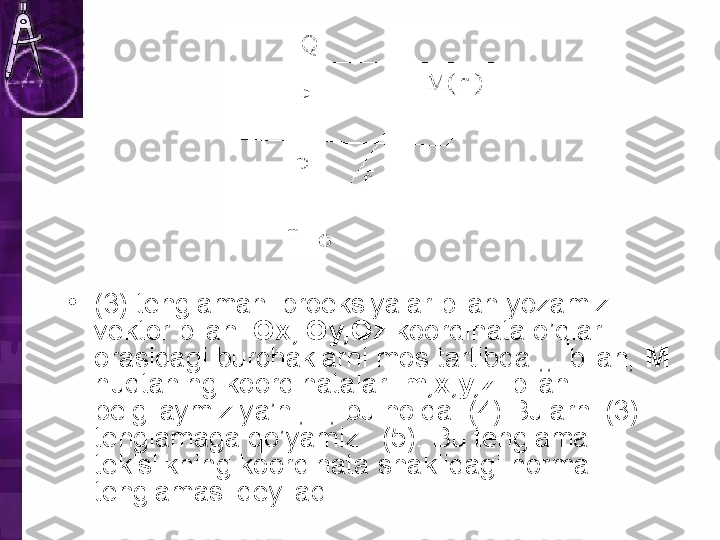
• (3) tenglamani proeksiyalar bilan yozamiz. … vektor bilan Ox, Oy,Oz koordinata o’qlari orasidagi burchaklarni mos tartibda ,, bilan, M nuqtaning koordinatalari m,x,y,z bilan belgilaymiz ya’ni, , bu holda (4) Bularni (3) tenglamaga qo’yamiz: (5). Bu tenglama tekislikning koordinata shaklidagi normal tenglamasi deyiladi.
