Geometriyadan burchaklarga doir mashqlar

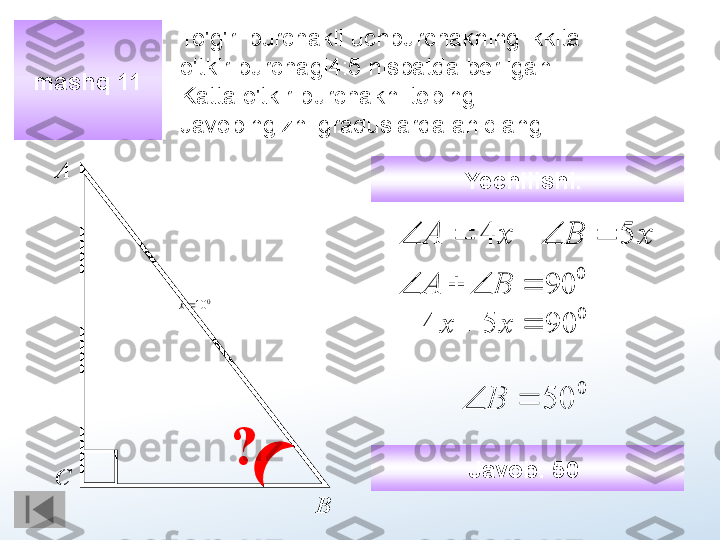






To'g'ri burchakli uchburchakning ikkita o'tkir burchagi4:5 nisbatda berilgan. Katta o'tkir burchakni toping. Javobingizni graduslarda aniqlang.mashq 11 А ВС ? Javob : 50 Yechilishi : х А 4 х В 5 0 90 В А 0 10х 0 90 5 4 х х 0 50 В
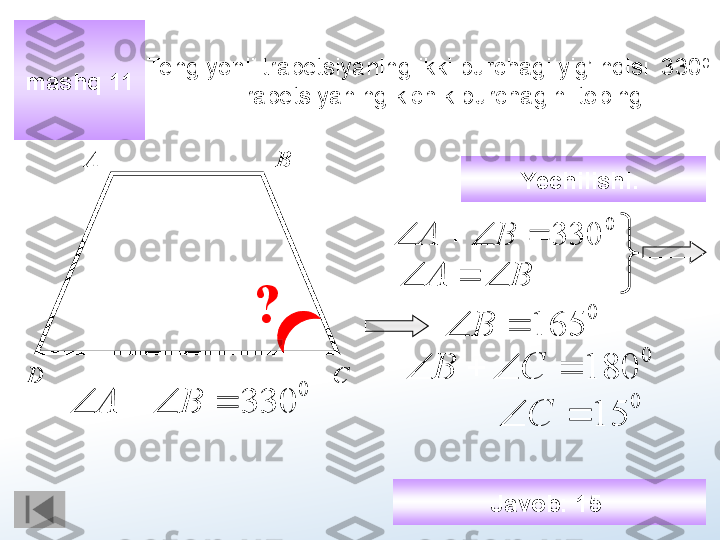
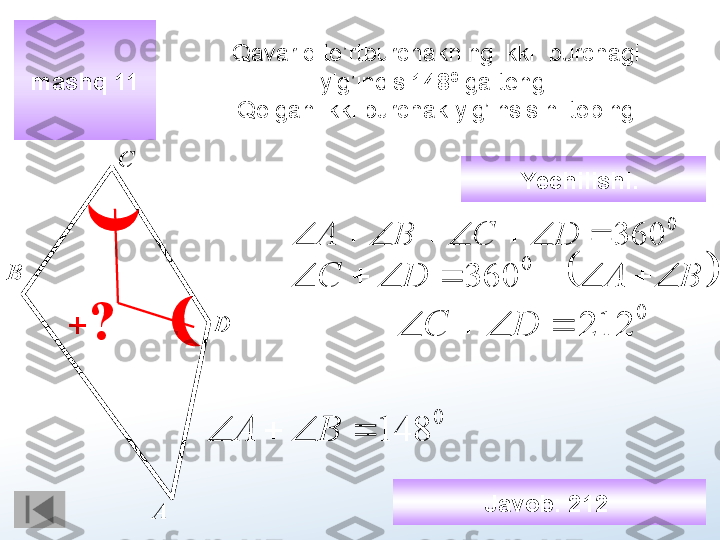
Parallelogrammning bir tomonida yotuvchi burchaklarining farqi ga teng. Paralelogrammaning kichik burchagini toping. Javobni graduslarda aniqlang.mashq 11 А В СD 0126 В А 0 180 ух 0 126 ух 0 306 2 х? Yechilishi : х А у В + 0 153х 0 27у Javob : 27
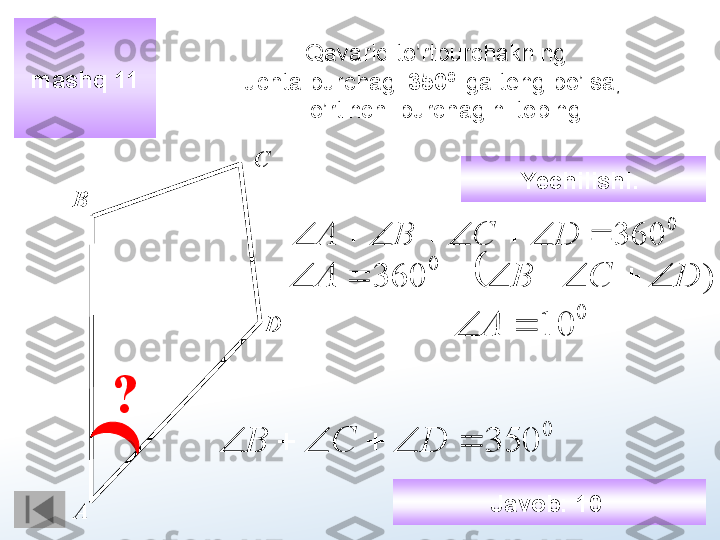
Parallelogramning bir burchagi ikkinchisidan 12 marta katta bo’lsa, Kichik burchagini (graduslarda) toping mashq 11 А В СDВ А 19 0 18019 хх? Yechilishi : х А 19 х В 0 9 х 0 180 20 х Javob : 9
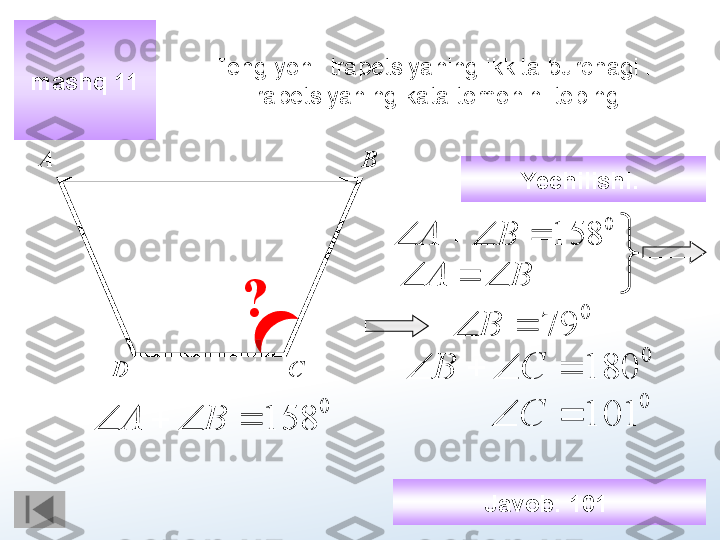
mashq 11 Teng yonli trapetsiyaning ikkita burchagi . Trapetsiyaning kata tomonini toping А В СD0 158 В А ? Yechilishi : 0 158 В А ВА 0 79 В 0 180 С В 0 101 С Javob : 101
