Sinus va kosinuslar teoremalari














Sinus va kosinuslar teoremalari
FRANSUA VIY ET (1540 -1603) Vi уе t t rigonomet riy ani y arat ilishida k at t a hissa qo'shgan. Ko'pgina t rigonomet rik formulalar birinchi mart a Viy et t omonidan y ozilgan. 1593 y ilda u k osinus t eoremasini og'zak i shak lda birinchi bo'lib y arat di Kosinus - bu lot in t ilidagi ex presssinus ifodasining qisqarishi, y a'ni " k omplement ar sinus" (y ok i boshqa y o'l bilan " t o'ldiruv chi y oy ning sinusi" ; cosa = sin (90 ° - a)).
Sin x v a cos x belgilari bilan zamonav iy sinus v a k osinus y ozuv lari birinchi mart a 1739 y ilda Bernulli t omonidan Sank t -Pet erburg mat emat igi L. Ey lerga y ozilgan xat da k irit ilgan. Ushbu belgilar juda qulay degan xulosaga k elib, ularni mat emat ik ishlarida ishlat a boshladi. Bundan t ashqari, Ey ler x burchak ning t rigonomet rik funk t siy alari uchun quy idagi qisqart malarni k irit adi: t ang x, cot x, sec x, cosecx.
Uchburchak y uzi formulasi Uchburchak ning y uzi uning ik k i t omoni v a ik k i t omoni orasidagi burchak ning sinusi y armiga t eng. CBCACBBCABS sin 21 sin 21 BAC CAB CACBAB sinsin sinsin A AC AB sin 2 1 AВС sin А В С
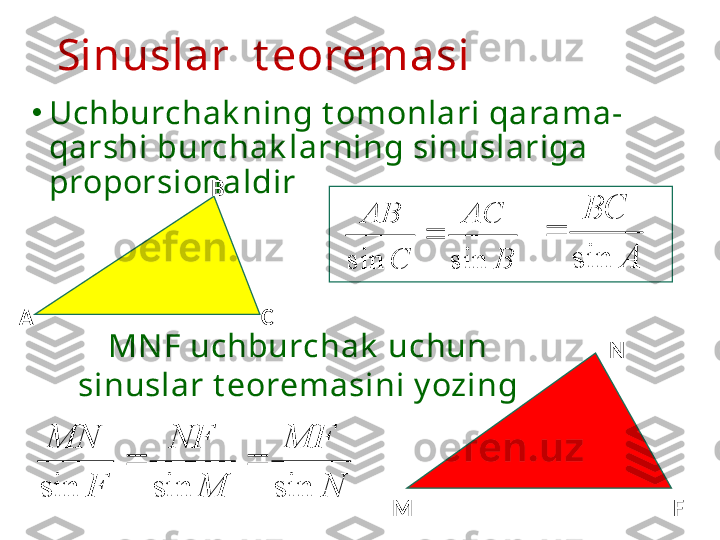
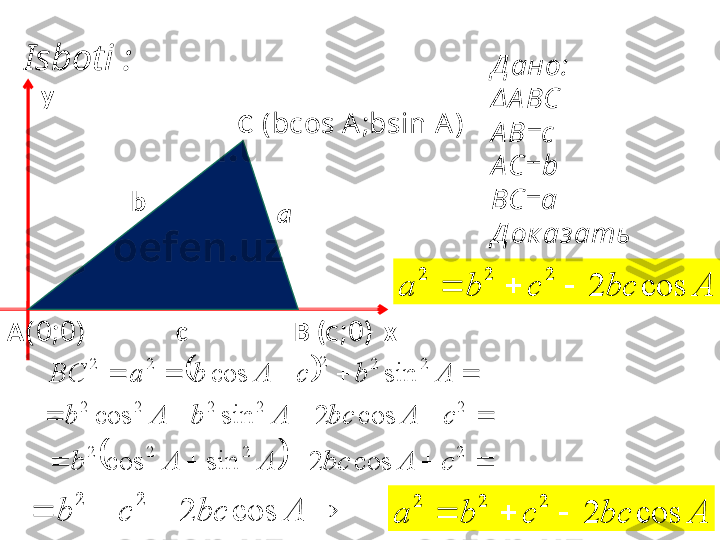
Sinuslar t eoremasi • Uchburchak ning t omonlari qarama- qarshi burchak larning sinuslariga proporsionaldir M FN NMF MNF FMN sinsinsin BAC CAB sinsin A ВС sin А В С MN F uchburchak uchun sinuslar t eoremasini y ozing
