NEFT VA GAZ KONLARINI BURG’ULASHDA HARORAT REJIMI MODELLARINI TADQIQ QILISH












i , k = r , φ , z ; ρ = σ
rr + σ
φφ + σ
zz
Harorot ta’sirida tog jinsining siljishi quyidagicha tenglama orqali
aniqlanadi:
∆u− u
r2+ 1
1−2μ
∂l
∂r+Fr
l− ρ
l
∂2u
∂z2= 2(1+μ)
1− 2μ
∂(αT )
∂r (1.12 )
Bunda
∆= ∂r
∂r2+1
2
∂
∂r+ ∂2
∂z2
l = ∂ u
∂ r + u
r ;
σ
ik − ¿
slindir sirtida kuchlanish komponentalari;
12](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_12.png)


![Quduq stvolining tekis deformatsiyalangan holati uchun temperatura kuch-
lanishlari quyidagi tenglamalardan aniqlanadi:
δrr= E
1−ϑ[
−1
r2∫r0
r
α∆Trdr + r2−r0
r2(R2− r02)∫r0
R
α∆Trdr ];
δθθ= E
1−ϑ¿
δ
zz = E
1 − ϑ ¿
(1.15) ifodalarni (1.16) formulalarga qo’yib, integrallab, ba’zi shakl
almashtirishlarni bajarib, quyidagilarni hosil qilamiz:
δ
rr = αBF
2 ( 1 − ϑ ) r 2 { 1
2
( r 2
− r 0 )
+ r 2
ln r
R + r
02
¿
δ
θθ = αBF
2
( 1 − ϑ ) r 2 ¿
δ
zz αBE
1 − ϑ ( 1 + 2 r
0 2
R 2
− r
02 ln r
0
R − 2 ln r
R )
Bunda α − ¿
termik kengayish koeffitsiyenti; E-stvoldagi tog’ jinsilarining
elatiklik moduli;
ϑ−¿ Puasson koeffitsiyenti.
Termik kuchlanishlarni baholash shuni ko’rsatadiki, quduqlarning mavjud
rejimlarida ular ancha katta qiymatlarda ega va ularning, boshqa mexanik
kuchlar bilan birgalikdagi ta’siri quduq stvoli atrofidagi tog’ jinslaridagi
kuchlanganlikni chegaraviy qiymatlarga yaqinlashish jarayonlarini
kuchaytiradi.
15](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_15.png)







![Quvurda kuchlanish quyidagi formulalar orqali aniqlanadi:
´σ
rr = 1
b 2
− a 2[ a 2
P
a ( 1 − b 2
r 2 ) − b 2
P
b ( 1 − a 2
r 2 )] ,
σφφ= 1
b2−a2[a2Pa(1+b2
r2)−b2Pb(1+a2
r2)],(2.22 )
(2.22) formulada (2.20a), (2.20b) tengliklarni qo’yib radial va aylanma
kuchlanishlarni quyidagicha aniqlaymiz:
´σ
rr = − 2 GK
b 2
− a 2
[ a 2 (
2 + 1
logβ )( 1 − b 2
r 2 ) − b 2
logβ ( 1 − a 2
r 2 )] = 2 GK [ 2
( b 2
r 2 − 1 )
β 2
− 1 + 1
logβ ] ,
´σφφ= −2GK
b2− a2[a2
(2+ 1
logβ )(1+b2
r2)− b2
logβ (1+a2
r2)]= 2GK [
−2(
b2
r2+1)
β2−1 + 1
logβ ],(2.23 )
Haqiqiy kuchlanishlar
σrr= σrr+´σrrva
σφφ=σφφ+´σφφ
Tenglikka asosan
σrr= 2GK [− 2
log b
r
logβ − 1
logβ +
2(
b2
r2−1)
β2−1 + 1
logβ ]=− 4GK [
log b
r
log b
a
−
b2
r2−1
b2
a2−1
]
σφφ=2GK [−2
log b
r
logβ + 1
logβ −
2(
b2
r2+1)
β2−1 + 1
logβ ]=− 4GK [
log b
r
log b
a
+
b2
r2+1
b2
a2−1
]
Normal kuchlanish quyidagicha bo’ladi:
23](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_23.png)
![σzz=−2G 1+μ
1− μαT +μ(´σrr+´σφφ)=−4GK
[
log b
r− μ
log b
a
+ 2μ
b2
a2−1]
.3-bob. QUDUQ DEVORIDA HARORATNING VAQT BO’YICHA
O’ZGARISHIDA HOSIL BO’LGAN KUCHLANISHNI HISOBLASH
3.1.Quduq devorida hosil bo’ladigan harorat natijasida hosil bo’lgan
kuchlanishni aniqlash.
Chuqur quduqlarni burg’ulashda quduq devorida harorat kuchlanishi sodir
bo’lib, devor ustuvorligiga katta ta’sir ko’rsatadi. Quduq devorida harorat
kuchlanishi aniqlash uchun avvola quduq devoridagi harorat almashinuv
qiymatini aniqlash kerak .Quduq devorida harorat almashinuvini aniqlashda
T.K. Malikov, A.I.Sherbon , V.P.Chernyak ishlari mavjud.
Quduq devorida issiqlik almashinuva quyidagi differensial tenglama orqali
aniqlanadi.
∂∆T(r,t)
∂t =a(
1
r
∂∆T
∂r +∂2∆T
∂r2 )(3.1 )
Bunda ∂ ∆ T
( r , t ) = T ( r , t ) − T
0
T0−¿
sirkulyatsiya qilinadigan suyuqlik harorati ;
r-quduq o’qi bo’ylab radius;
a−¿
tog’ jinsining issiqlik o’tkazuvchanlik koeffitsiyenti;
24](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_24.png)
![Bu holda sirkulyatsiya qilinadigan suyuqlik harorati natijasida quduq
devorida vaqtga bog’liq natijasida harorat o’zgarishi quyidagi formula orqali
aniqlanadi. [7]
T=T0−(T0−Tc)√
rc
rerfc r−rc
2√at (3.2 )
Formula orqali aniqlanadi, bu yerda
erfcx =1− 2
√π∫0
x
e−t2dt (3.3 )
Tc−¿
tog’ jinsi devoridagi boshlang’ich harorat;
Quduq devorida hosil bo’ladigan deformatsiya quyidagicha aniqlanadi:
e
rt = 1
E [
σr− μ(σθ+σz) ]+
αT ( r ) ;
e
θ t = 1
E [ σ
θ − μ ( σ
r + σ
z )
]+
αT ( r ) ; (3.4)
e
zt = 1
E [
σz− μ(σθ+σr) ]+ αT (r);
Bu yerda
eθ,er,ez−¿ nisbiy deformatsiya;
σ
r − ¿
radial kuchlanish;
σ
θ − ¿
aylanma kuchlanish;
σ
z − ¿
vertikal kuchlanish;
σ
rt E
( 1 + μ ) ( 1 − 2 μ )
[( 1 − μ ) ε
rt + μ ε
θ t + μ ε
z t − ( 1 + μ ) αT ( r ) ] ;
σ
θt E
( 1 + μ ) ( 1 − 2 μ )
[( 1 − μ ) ε
θt + μ ε
r t + μ ε
z t − ( 1 + μ ) α ( T ) r ]
;
σ
zt E
( 1 + μ ) ( 1 − 2 μ )
[( 1 − μ ) ε
zt + μ ε
θt + μ ε
r t − ( 1 + μ ) αT ( r ) ] ;
(3.5)
25](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_25.png)



![Demak (1− μ) (A1+c1− c2
Rt2+A2¿+μ¿ + c2
Rt2− A1¿+μA3−(1− μ)A2 =0 (3.21)
(3.21) tenglamadan foydalanib o’zgarmas c
1 va
c2 larni
topamiz.
c
1 = μ
R
t2
− r
c 2 ¿
+ 2 A
2 R
t2
¿ − A
1 R
t2
(
1 − 2 μ )
R
t2
− r
c2 ;
(3.22)
c
2 = μ r
c R
t2
( A
4 − r
c A
3 + 2 r
c A
2 )
(
1 − 2 μ ) ( R
t2
− r
c 2
) − A
1 R
t2
R
t2
− r
c2
(3.23)
Aniqlangan c
1 va c
2 larni kuchlanish formulalariga qo’yamiz:
σ
rt = E
(
1 − μ )( 1 − 2 μ ){( 1 − μ )[
( 1 + μ )
(
1 − μ ) αT ( r) − 1
r 2 1 + μ
1 − μ ∫
r
cr
αT ( r) + c
1 − c
2
r 2 ] + μ [ 1
r 2 1 + μ
1 − μ ∫
r
cr
αT ( r) rdr + c
1 + c
2
r 2 ] + μ 2
r 2
− r
c2 ∫
r
cr
αT ( r) − ( 1 + μ ) αT ( r)} ;
(3.24)
σ
θt = E
(
1 − μ )( 1 − 2 μ ) { (1− μ)[
1
r2
1+μ
1− μ∫rc
r
αT (r)rdr +c1+c2
r2]− μ¿
σzt= E
(1− μ)(1−2μ) {
(1− μ) 2
r2−rc2∫rc
r
αT (r)dr +μ[
1
r2
1+μ
1− μ∫rc
r
αT (r)dr ¿+c1+c2
r2¿]+μ[
1+μ
1− μαT (r)− 1
r2
1+μ
1− μ∫rc
r
αT (r)rdr ¿+c1− c2
r2¿]−(1+μ)αT (r)};
(3.25)
Jadvalda ba’zi tog’ jinslarining elastiklik va teplofizik qiymatlari keltirilgan
[4].
29](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_29.png)
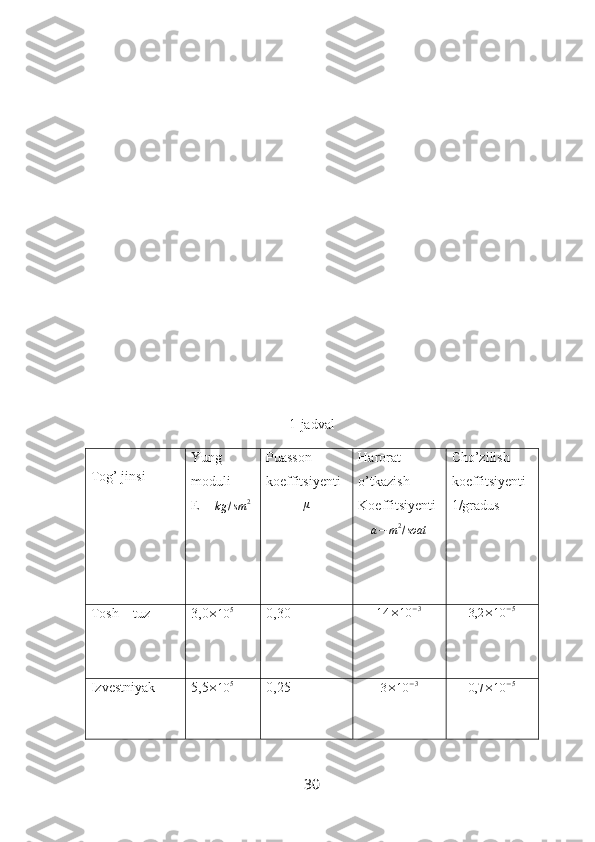




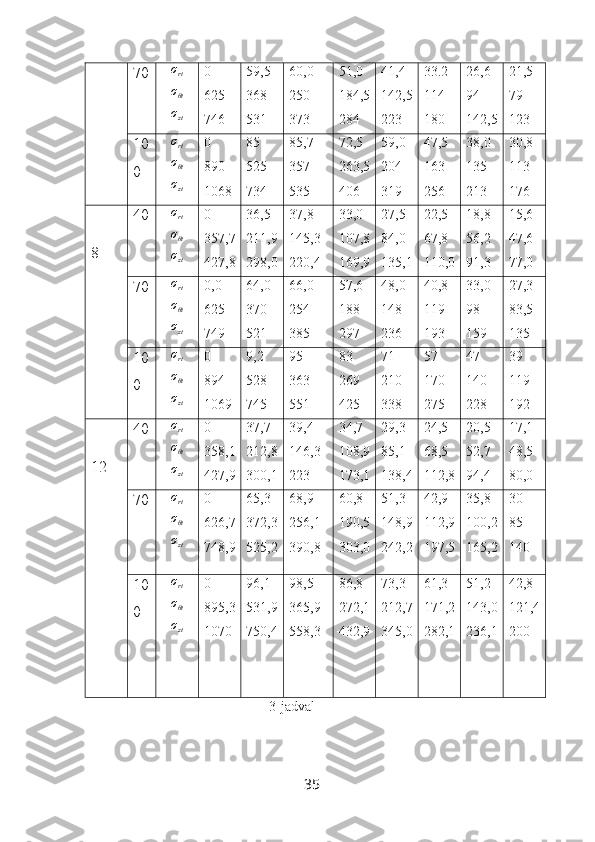


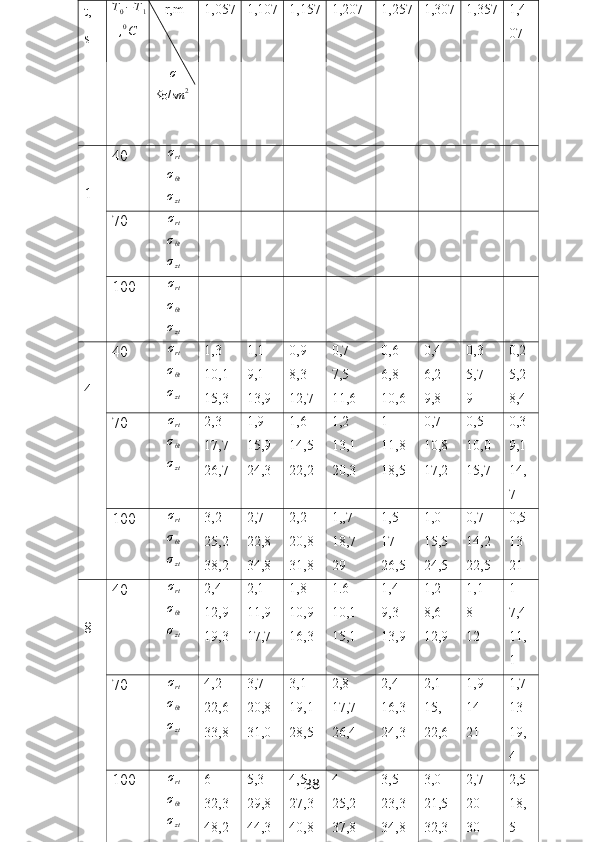







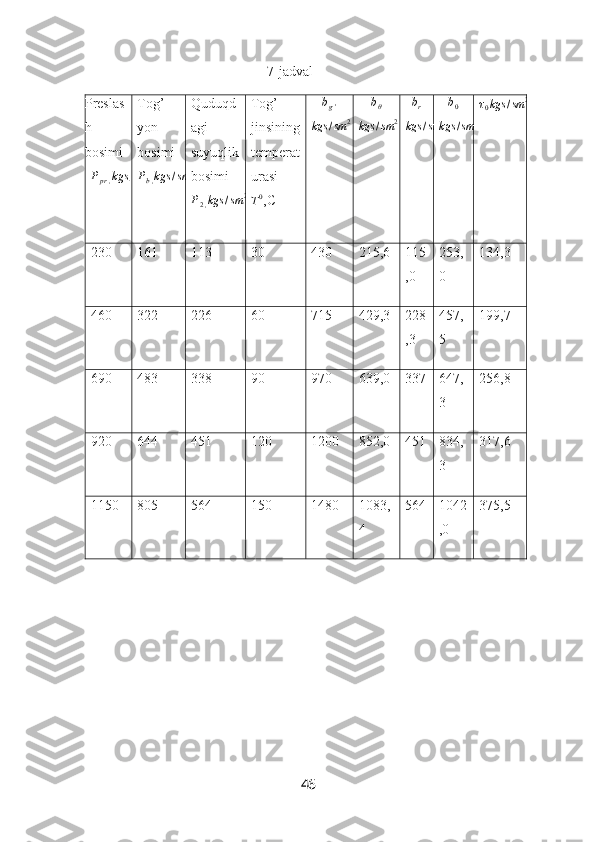




![r = R da ϑ T
rϑ = 0 ( 3.28 )
Temperatura bir tekis o’zgarishini hisobga olib, (3.26),(3.27) masalani
masalani yechish uchun o’rtalashtirish usulini qo’llash mumkin. Bu usulga
muvofiq quyidagicha yozamiz:
ϑ T
ϑ t = 1
r ϑ T
ϑ r +
ϑ2T
ϑr2=φt= 1
R−1∫1
RϑT
ϑtdr (3.29)
φ(t)= aT0
r02 (φt) (3.29) tenglamadan :
T
( r , t ) = ( φ t ) r 2
4 + C
1 ln r + C
2 (3.30)
Chegaraviy shartlar yordamida
C1va C2 aniqlagach ushbuni olamiz:
T(r,t)= φt
2 [
r2
2− R2ln r+R2
m − 1
m− 1
2]+T1 (3.31)
(3.31) formulani φ t
ning ifodasiga qo’yamiz. Unda
φt= φI(t)
2(R−1)∫
1
R
[
r2
2−(ln r− 1
m )R2−(
1
m +1
2)]dr;
d φ t
φ t = a
0 d t ;
( φ t ) = C
3 e a
0 t
,
(3.32)
Bunda
a0= 2(R−1)
R3−1
6 − 1
2(R−1)− R3(ln R−1)− R2+(R−1)(R2−1)1
m
Integrallash o’zgaruvchisi C
3 ni
51](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_51.png)
![t = 0 da T = a
2 [ 1
2( r 2
− 1 ) − R 2
ln r + 1
m ( R 2
− 1 ) ]
Shartdan aniqlaymiz:
C3=¿ a0
(3.33)
Unda
φ(t)=a0ea0t
(3.33) ifodani (3.31) ga qo’yib quyidagini olamiz :
∆T ( r,t )= T ( r,t )- T1= a0
2 ea0t
[
1
2(r2−1)− R2ln r+1
m (R2−1)]. (3.34)
(3.32) ifoda yordamida temperatura farqini topgach , uning ta’sirida quduq
stvoli atrofida yuzaga keluvchi kuchlanganlik va deformatsiyalanish holatini
aniqlash mumkin.
Quduq stvolining tekis deformatsiyalanish holati uchun sovish holati
uchun kuchlanishlarni quyidagi formulalardan aniqlanadi:
δ
r = − E
1 − ϑ
( − 1
r 2 ∫
r
0r
α ∆ Trdr + r 2
− r
02
r 2 (
R 2
− r
02 ) ∫
r
0R
α ∆ Trdr ) ;
δ
θ = − E
1 − ϑ
( − 1
r 2 ∫
r
0r
α ∆ Trdr + r 2
+ r
0 2
r 2 (
R 2
− r
02 ) ∫
r
0R
α ∆ Trdr ) ;
¿δz= − E
1−ϑ(
2ϑ
R2− r02)∫r0
R
α∆Trdr +(1−ϑ)εz−α∆T; (3.35)
ε
z miqdorni qaralayotgan elementni cho’zuvchi bo’ylama kuchni nolga
tenglashtirib topish mumkin:
P=
2π∫r0
R
δzrdr = 0 bundan
52](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_52.png)
![ε
z = 2
R 2
− r
02 ∫
r
0R
α ∆ Trdr
Va δz uchun quyidagi ifodani olamiz:
δ
z = − E
1 − ϑ ¿
(3.36)
(3.35) va (3.36) tenglamalarni o’lchovsiz miqdorlar yordamida yozamiz:
δ
r = − 1
r 2
[ r 2
− 1
R 2
− 1 ∫
1R
∆ T r d r
∫
1r
∆ T r d r ] ;
δ
θ = − 1
r 2 ¿
] (3.37)
δz= −1
r2[ 2r2
R2−1∫1
R
∆Trdr− ∆Tr2] .
(3.37) ifodalarga (3.34) formula yordamida topilgan temperatura farqini qo’yib,
o’lchovsiz temperatura kuchlanishlari uchun quyidagilarni olamiz:
δr= 1
4a0ea0t
[(1− 1
r2)A− R2ln r+1
4(r2−1)];
δ
θ = 1
4 a
0 e a
0 t
[
r 2
− ( 1 − 1
r 2 ) A − R 2
ln r − 1
4 ( r − 1 ) − A
1 ] ;
(3.38)
δz= 1
4a0ea0t
[
r 2
− ¿ 2 R2ln r− A1¿;
Bunda
A= 1
R 2
− 1
[ R 2 (
ln R − 3
4 ) + R 2
− 1
4 ] + R 2
2 − 1
4 ;
53](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_53.png)
![A
1 =1+ 1
2(R2−1)[R2(3− 4ln R)−4]R2+1;
(3.38) formula yordamida issiqlik ta’siri radiusi va nostatsionar temperatura
kuchlanishlarini hisoblash uchun turli tog’ jinslarining teplofizik parametrlari
qiymatlarini va jinslar bilan suyuqlik o’rtasidagi issiqlik almashish
koeffitsiyentini halqaviy soha uchun aniqlash zarur bo’ladi.Issiqlik almashish
koeffitsiyentini odamda Nusselt kretiriyasi orqali topiladi.
A.X.Mirzajonzoda quduqlardagi issiqlik hisoblashlari uchun Nusselt
kretiriyasining quyidagi taqribiy qiymatlarini tavsiya etgan.
- Doiraviy truba uchun Nu=4,47;
- Tekis truba uchun Nu=4,29;
Sh.F.Mextiyev, A.X.Mirzajonzoda (va boshqalar) ning ishida halqa soha
uchun Nusselt sonining taqribiy qiymqti aniqlangan: Nu=4,38;
Issiqlik almashish koeffitsiyenti h- halqa sohadan strukturaviy oqim uchun
(burg’ulash amaliyotida oqim strukturaviy bo’lishi kuzatilgan) ushbu
h = Nu ∗ K
gr
D − d
formuladan topiladi,bunda K
gr − ¿
loyli burg’ulash suyuqligining issiqlik
o’tkazish koeffitsiyenti,D- quduq diametri; d-burg’ulash kolonnasining tashqi
diametri;
Turli xususiyatlarga ega loyli burg’ulash suyuqliklarning issiqlik
o’tkazish koeffitsiyenti yetarlicha o’rganilmagan. Ammo V.N. Daxnov va
D.I.D’yakanovlarning tekshirishlari ko’rsatadiki, loyli burg’ulash suyuqligining
solishtirma issiqlik qarshiligi
54](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_54.png)

![Bunda T-tog’ jinsi harorati; t-vaqt; z-vertikal koordinatasi; a − ¿
harorat
uzatish koeffitsiyenti;
Quduq tubida suyuqlik harorati quyidagicha o’zgaradi deb qaraymiz:Tz=T0cos 2πnτ
τ0
=T0cosωτ
(3.40)
T0−¿
quduq tubi sirtida suyuqlik harorati;
(3.39) tenglamaning chegaraviy shartlarini qanoatlantirishi kerak.Quduq tubi
sirti issiqlik konveksiyasi natijasida,quyidagi shartlar bajariladi.
Bunda k-tog’ jinsining sirtida issiqlik o’tkazuvchi koeffitsiyenti;
h-issiqlik almashinuv koeffitsiyenti;
Quduq tubi sirtida chegaraviy shart quyidagicha :
k ∂ T
∂ z = − h ( T − T
z )
(3.41)
(3.39) tenglamaning yechimini quyidagicha yozish mumkin[7].
T = ∁ e −
√ 1
2 z
∗ cos ( aτ − √ 1
2 z − B ) ( 3.42 )
C va B lar boshlang’ich va chegaraviy shartlarda aniqlanadi.
Masalaning yechimi quyidagicha :
56](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_56.png)
![T = T
0 e −√ πn
a τ
0 z
√
1 + 2 √ πn k 2
a τ
0 h 2 + 2 πn k 2
a τ
0 h 2 ×
×cos
[
2πnτ
τ0
−√
πn
aτ0
z− arctg
(
1
1+
√
aτ0h2
πn k2)]
;(3.43 )
Quduq tubi sirtida haroratning o’garishi quyidagicha bo’ladi:
Tz=0= T0
√
1+2
√
πn k2
aτ0h2+2 πn k2
aτ0h2
cos 2πnτ
τ0
(3.44 )
Agar kriteriy BIO ni
B
i 2
= a τ
0 h 2
πn k 2
Deb olsak ,tog’ jinsining harorat o’tkazichi katta bo’lsa , ya’ni Bio sonining
katta qiymatida
z
max = 2 τ
√ πn a
τ
0 = 2 τ √ ωa
2 = τ √ 2 ωa
, (3.45)
bo’ladi
Bio sonining kichik qiymatlarida haroratning tebranishini quyidagicha
yozish mumkin:
zmin = √πn aτ0
πn (
2πnτ
τ0
− π
4)=τ√2ωa − π
4√
2a
ω .(3.46 )
bo’ladi.
Issiqlik tebranishi tog’ jinslarida z
min dan z
max gacha o’zgaradi.
57](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_57.png)

![×
[
T0e−ω0z
√
1+ 2
Bi + 2
Bi 2
cos (ωτ −ω0z−arctg 1
1+Bi )−To'rt
]
,(3.51 )
σzz= 2μ
1−3μαE ×
×
[
T0e−ω0z
√
1+ 2
Bi + 2
Bi 2
cos (ωτ −ω0z−arctg 1
1+Bi )−To'rt
]
,(3.52 ) Bunda ω
0 =
√ πn
a τ
0 ; ω = 2 πn
τ 0 va Bi 2= aτ0h2
πn k2
Tog’ jinsi sirtida hosil bo’lgan kuchlanishlar quyidagicha bo’ladi:
σ
xx = σ
yy =
( 1 − 2 μ
1 − 3 μ ) αE
[ T
0√
1 + 2
Bi + 2
Bi 2 cos ωτ − T
o ' rt ] ,
( 3.53 )
σzz=(
2μ
1−3μ)αE
[
T0
√
1+ 2
Bi + 2
Bi 2
cos ωτ −To'rt
]
(3.54 )
3.6.Quduq tubi sferik holda kuchlanishlarni aniqlash
Ko’p hollarda quduq tubi yassi holda bo’lmasdan sferik ko’rinishda
bo’ladi. Sferik shakldagi quduq tubi uchun harorat tenglamasi quyidagicha
bo’ladi:
∂T
∂τ= a(
2
r
∂T
∂r+∂2T
∂r2)(3.55 )
59](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_59.png)
![Sferik shaklda bo’lgan quduq tubi radiusi r = r
0 da chegaraviy shart
quyidagicha yoziladi.T(r0,τ)=T0cosωt (3.56 )
(3.55) tenglamada yangi o’zgarish
ϑ = rT ( r , τ )
kiritib quyidagi tenglamani hosil qilamiz.
∂ ϑ
∂ τ = a ∂ 2
ϑ
∂ r 2
( 3.57 )
Chegaraviy shart quyidagicha bo’ladi.
ϑ=(r0τ)= r0τ0cosωτ (3.58 )
(3.57) tenglama (3.58) shart orqali quyidagi yechimni hosil qilamiz.
ϑ(r,τ)=T0r0e−√ω2a(r−r0)cos [ωτ −√
ω
2a(r− r0)].(3.59 )
Yangi o’zgaruvchini hisobga olganda harorat qiymati quyidagicha aniqlanadi
Differensial tenglama (3.55) ning (3.56) chegaraviy shartda yechimi
quyidagicha yoziladi:
T
( r , τ ) = r
0 T
0
r e − √ ω
2 a
cos [ ωτ − √ ω
2 a ( r − r
0 )]( 3.60 )
Bu holda haroratning eng katta qiymati
[ωτ − √
ω
2a(r− r0)]=0 bo’ladi.
Bundan R = r
0 + τ
√ 2 ωa ( 3.61 )
Sferik tubda hosil bo’ladigan kuchlanishlar quyidagi formula orqali
o’rganiladi. Bu formuladan ko’rinadiki,harorat ta’siri radiusi sirkulyatsiya vaqti
tog’ jinsi harorat o’tkazuvchanligi va yuvish chastotasiga bog’liqdir.
60](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_60.png)
![Harorat radius ta’sirining qonuniyatlarini bilib hosil bo’ladigan
kuchlanishni aniqlanadi. `
σ
rr = 2 S
1 − 2 μ[( 1 − μ ) ∂ u
∂ r + 2 μ u
r − ( 1 + μ ) a ∆ T ] ;
σφφ=σθθ= 2S
1−2μ[
u
r+μ∂u
∂r−(1+μ)a∆T](3.62 )
Kuchlanishlar muvozanat tenglamasi quyidagicha bo’ladi.
∂σrr
σr
+2
r(σrr− σθθ)=0;
σ
φφ = σ
θθ ( 3.63 )
(3.61) va (3.63) tengliklardan kuchlanish natijasida tog’ jinsining siljishi
uchun quyidagi tenglamani hosil qilamiz.
∂
∂ r
[ 1
r 2 ∂
∂ r ( u r 2 )]
= ∂ 2
u
∂ r 2 + 2
r ∂ u
∂ r − 2 u
r 2 = ( 1 + μ
1 − μ ) α ∂ ∆ T
∂ r ( 3.64 )
(3.64) tenglamani integrallab quyidagini hosil qilamiz.
u = a
r 2 ∫
r
0r
∆ T
( r , τ ) r 2
dr ;
∂ u
∂ r = a ∆ T ( r
1 τ ) − 2 a
r 3 ∫
r
0r
∆ T ( r , τ ) r 2
dr
(3.65)
(3.65) tenglamalardan siljish qiymatlarini (3.62) ga qo’yib quyidagi
tangensianal kuchlanishlar quyidagicha topiladi:
σ
rr = − 2 aE
(
1 − μ ) r 3 ∫
r
0r
∆ T ( r , τ ) r 2
dr ;
σφφ=σθθ= dE
1− μ[
1
r3∫r0
r
∆T(r,τ)r2dr − ∆T(r,τ)](3.66 )
Suyuqlik o’rtacha harorati
To'rt va tog’ jinsi harorati orasidagi farq
quyida-gicha bo’ladi:
∆ T
( r , τ ) = T ( r , τ )
- T
o ' rt (3.66)
61](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_61.png)
![(3.60) va (3.66) haroratni hisobga olib (3.65) formulaga qo’yib
integrallashdan keyin kuchlanishlarni aniqlaymiz.
σ
rr = aE T
0 r
0 e − ω
0 ( r − r
0 )(
1 − μ ) r 3 { r
ω
0 ¿
(3.67)
σ
θθ = aE
1 − μ T
0 r
0 e − ω
0
( r − r
0 )
r 3 { B
0 e ω
0 ( r − r
0 )
− r
2 ω
0 ¿
ω0=√
ω
2a ;
B
0 = 5
2 ω
0 [ r
0
( sinωτ + cosωτ ) + sinωτ
ω
0 ]
Quduq tubi sferik holati uchun radial kuchlanish 0 ga teng.
Tangensianal kuchlanish esa quiyidagicha bo’ladi:
σ
θθ = aE
1 − μ
( T
o '
rt − T
0 cosωτ ) = aE T
o '
rt
1 − μ ( 1 − T
0
T
o '
rt cosωτ )( 3.69 )
Quduq tubi tekis yuza va sferik sirtlardan farq qilgani uchun
kuchlanishning garmonik tebranishi (3.51),(3.52) formula va (3.68),(3.69)
qiymatlarni o’rtasida bo’ladi. Hisoblash oson bo’lishi uchun quduq tubi
yuzasida z=0 kuchlanishlarni quyidagicha yoziladi.
Yuqoridagi keltirilgan formulalarni o’lchovsiz holda yozamiz, hisoblashlar
oson bo’lishi uchun kuchlanishlarni quduq tubi sirti va maksimal chuqurlikdagi
uchun yozamiz.
Tekis kuchlanish holati uchun z = 0
quyidagicha:
62](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_62.png)
![σxx= σxx= σyy
(
1−2μ
1−3μ)αE Tcr
=−
[
1− T0
Tcr
cos 2π τ
τ0
√
1+ 2
Bi
+ 2
Bi2]
;
σ
zz = σ
zz
2 μ
1 − 3 μ αE T
cr = −
( 1 − T
0
T
cr cos 2 π τ
τ
0 √
1 + 2
B
i + 2
B
i2 ) ( 3.70 )
Maksimal chuqurlik uchun quyidagi formula hosil qilamiz:
σxx= σxx= σyy
(
1−2μ
1−3μ)αE Tcr
=−
(
1− T0
Tcr
e
−2πττ0
√
1+ 2
Bi
+ 2
Bi2)
;
σzz= σzz
2μ
1−3μαE Tcr
=
(
1− T0
Tcr
e
−2πττ0
√
1+ 2
Bi
+ 2
Bi2)
(3.71)
Quduq tubi sferik holdagi uchun
r= r0da σrr= 0
σφφ=σθθ= σφφ= σθθ
αE Tcr
1− μ
=1− T0
Tcr
cos 2π τ
τ0
(3.72 )
r=R da
σφφ=σθθ= σθθ
αE Tcr
1− μ
=
T0
Tcr
¿¿
63](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_63.png)
![+r0cosωτ ¿−r0[
1
2√
2a
ω −(r0+τ√2ωa ¿2]e−ωτ
}+¿+ 1 + 1
3 ∗ ¿
(3.70) formulaning grafigi
>
>
>
>
64](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_64.png)



![ω = 31
.chastota σxx= σxx= σyy
(
1−2μ
1−3μ)αE Tcr
=−
[
1− T0
Tcr
cos 2π τ
τ0
√
1+ 2
Bi
+ 2
Bi2]
;
σ
zz = σ
zz
2 μ
1 − 3 μ αE T
cr = −
( 1 − T
0
T
cr cos 2 π τ
τ
0 √
1 + 2
B
i + 2
B
i2 ) ( 3.70 )
Quduq tubi sferik holdagi uchun
r= r0da σrr= 0
σφφ=σθθ= σφφ= σθθ
αE Tcr
1− μ
=1− T0
Tcr
cos 2π τ
τ0
(3.72 )
r=R da
σφφ=σθθ= σθθ
αE Tcr
1− μ
=
T0
Tcr
¿¿
+ r
0 cosωτ ¿ − r
0
[ 1
2 √ 2 a
ω − ( r
0 + τ √ 2 ωa ¿ 2 ]
e − ωτ }
+ ¿
+ 1 + 1
3 ∗ ¿
Hisoblash qiymatlari rasmlarda keltirilgan.
r0=0,135 ;
ω=31 ch ;
68](/data/documents/6dea3260-7b65-46a7-b623-2ce1c691a400/page_68.png)









NEFT VA GAZ KONLARINI BURG’ULASHDA HARORAT REJIMI MODELLARINI TADQIQ QILISH MUNDARIJA KIRISH………………………………………………………..…………………4 I BOB. NEFT VA GAZ KONLARINI BURG’ULASHDA HARORATNING QUDUQ DEVORIGA TA’SIRINING TAHLILI 1.1.Quduqda suyuqlik haroratining burg’ulangan tog’ jinsiga bo’lgan ta’sirining o’rganilganlik holati……………….. …………………………………………….6 1.2.Harorat maydoni orqali hosil bo’ladigan termoelastik kuchlanish tenglamalari……………………………………………………………………...1 1.3. Quduq devori tog’ jinslarining ichki konveksiya hisobiga olingandagi statsionar termoelastik kuchlanganlik holati…………. ………………………...14 II BOB. QUDUQ DEVORIDA STATSIONAR HARORAT KUCHLANISHI 2.1.Statsionar harorat ta’sirida hosil bo’ladigan kuchlanish …………………… 17 2.2.Devori qalin slindr quvurida harorat kuchlanishi…………………….....21 III BOB. QUDUQ DEVORIDA HARORATNING VAQT BO’YICHA O’ZGARISHIDA HOSIL BO’LGAN KUCHLANISHNI HISOBLASH 3.1.Quduq devorida hosil bo’ladigan harorat natijasida hosil bo’lgan kuchlanishni aniqlash…………………………………………………………...25 3.2.Burg’ulash jarayonida hosil bo’lgan quduq devorida kuchlanishning tahlili……………………………………………………………………………45 1
3.3.Chuqur quduqlarning issiqlik rejimi hamda uning zaboy va quduq devori yemirilishlariga ta’siri…………………. ………………………………………………………...47 3.4. Quduq stvolining sovishi va isishi natijasida yuzaga keladigan quduq devori tog’ jinslaridagi nostatsionar temperatura kuchlanishlar ……….. ………………………………………………………………………...49 3.5. Burg’ulashda kuchlanishlarning quduq tubida davriy o’zgarishi…………… ………………………………………………………….55 3.6.Quduq tubi sferik holda kuchlanishlarni aniqlash…………………………………………………………………………59 XULOSA ………………………………………………….…………………...70 FOYDALANILGAN ADABIYOT …………..……………………………….71 ILOVA ……………………………………...………………………………….73 2
Kirish Mavzuning dolzarbligi: Neft va gaz konlarini burg’ulashda quduq chuqurligi oshgan sari yerning geotermik gradienti oshib boradi. Burg’ulash jarayonida qazilgan tog’ jinsini yer yuziga olib chiqish uchun maxsus yuvish suyuqligi quduqqa haydalanadi. Yer sathida suyuqlik ma’lum bir haroratga ega bo’ladi. Suyuqlikning quduqda sirkulyatsiya natijasida quduq devoridagi tog’ jinsi harorat almashinuvi natijasida uning harorati suyuqlik haroratiga qadar kamayadi. Natijada tog’ jinsining harorati doimiy ravishda o’zgarib turadi.Tog’ jinsida haroratning o’zgarishi vaqt bo’yicha o’zgaruvchi kuchlanishlarga keltiradi. Bu kuchlanishlar tog’ jinsida xoliqishga kelib quduq devori o’z ustuvorligini yuqotib, yemirilishga olib keladi. Natijada devor qatlamlarining ag’anab turishi yoki quduq devori torayishi va boshqa asoratlar sodir bo’ladi. Chuqur quduqlarni burg’ulashda harorat ta’sirida quduq devorining ustuvorligiga bo’lgan ta’sirini o’rganish muhim ahamiyatga ega. Yuqorida keltirilgan mulohazalarga asosan neft va gaz konlarini qazishda burg’ulash suyuqligining haroratining ta’sirida hosil bo’ladigan kuchlanishlarni aniqlash dolzarb masalalardan hisoblanadi. Tadqiqotning maqsadi : Burg’ulash suyuqligining quduq harakatidagi quduq devorida sodir bo’ladigan harorat kuchlanishini tadqiqot qilish . Tadqiqotning vazifalari: Neft va gaz quduqlarini burg’ulash jarayonida yuvish suyuqligi haroratining quduq devorida hosil bo’ladigan kuchlanishning 3
xususiyatlari va o’rganilganlik holatini tahlil qilish.Statsionar issiqlik almashinuvi natijasida sodir bo’ladigan kuchlanishlarni va tog’ jinsi bilan nostatsionar issiqlik almashinuvi hosil bo’ladigan kuchlanishlarni aniqlash va sonli tahlil qilish. Tadqiqotning obyekti sifatida neft va gaz konlarini burg’ulashda quduqni yuvish suyuqligi va quduq devoridagi tog’ jinsi harorat almashinuvida hosil bo’ladigan kuchlanish. Tadqiqotning yangiligi: 1.Neft gaz konlarini burg’ulashda yuvish suyuqligining statsionar oqimi uchun tog’ jinsida sodir bo’ladigan kuchlanish qiymatlari aniqlanadi va sonli hisob qilinadi. 2.Yuvish suyuqligini harorati ta’siri nostatsionar harakatida tog’ jinsida tuz, qum, izvestnyaklarda harorat ta’sirida hosil bo’ladigan radial aylanma kuchlanishlar. 3.Burg’ulash jarayonida quduq tubi sathida harorat almashinuv natijasida tekis quduq tubi va sferik shakldagi quduq tubida sodir bo’ladigan kuchlanishlar aniqlanadi. Tadqiqotning ilmiy va amaliy ahamiyati: Tadqiqot natijalarining ilmiy ahamiyati neft va gaz konlarini burg’ulashda suyuqlikning quduqda sirkulyatsiya jarayonida tog’ jinsida sodir bo’ladigan kuchlanishlarni hisoblashdan iborat. Tadqiqot natijalarining amaliy ahamiyati : quduqlarni burg’ulash sohasida mutaxassislar uchun quduq devori tog’ jinsilarining ustuvorligini oshirish uchun ishlatishi mumkin. 4
Dissertatsiyaning tuzulishi va hajmi : Kirish qismi, uchta bob,xulosa,foydalanilgan adabiyotlardan tashkil topgan bo’lib 70 betdan iborat. 1-bob.NEFT VA GAZ KONLARINI BURG’ULASHDA HARORATNING QUDUQ DEVORIGA TA’SIRINING TAHLILI 1.1.Quduqda suyuqlik harakatining tog’ burg’ulangan jinsiga bo’lgan ta’sirining o’rganilganlik holati. Quduqlarni burg’ulashda suyuqlik haroratining o’zgarishi va uning tog’ jinsiga bo’lgan ta’sirini olimlardan A.X.Mirzajonzoda, E.B.Chekalyuk, A.N. Sherban, A.I. Bo’latov, G.G.Gabuzov, N.S.Timofeev, I.A.Charniy, S.M.Kuliyev, B.I.Esman, Yarimiychuk kabi va boshqa olimlar tomonidan o’rganilgan. Chuqurlikda joylashgan neft va gaz konlarni burg’ulashda geotermik qonuni-ga asosan quduq harorati oshib boradi. Haroratning oshishi quduq devori ustuvorligiga ta’sir etib burg’ulash texnologiyasiga ta’sir etadi. Oxirgi yillarda haroratning quduq ustuvorligiga ta’siri bo’yicha ko’pgina ilmiy izlanishlar olib borilgan. Quduqlarni burg’ulashda uning devori murakkab kuchlanishlar holatida bo’ladi. Quduqda haroratning ozgina o’zgarish va harorat kuchlanishi kam bo’lib, haroratlar ayirmasi oshgan sari quduq devoriga cho’ziluvchan kuchlanishlar sodir bo’ladi. Timofeev ishda burg’ulash jarayonida haroratning o’zgarishi hosil bo’ladigan kuchlanishlar, quduq devorining harorat o’zgarishi bilan ustuvorligi masalalari qaralgan. 5
