logo
  1. Главная страница
  2. Дипломные работы
  3. Общий
  4. ISHLAB CHIQARISHNI REJALASHTIRISH MASALASINI TADQIQ QILISH VA DASTURIY TA’MINOTINI YARATISH

ISHLAB CHIQARISHNI REJALASHTIRISH MASALASINI TADQIQ QILISH VA DASTURIY TA’MINOTINI YARATISH

Загружено в:

12.08.2023

Скачано:

0

Размер:

1249.5703125 KB
Скачать
ISHLAB CHIQARISHNI REJALASHTIRISH MASALASINI TADQIQ QILISH VA DASTURIY TA’MINOTINI YARATISH 1 MUNDARIJA KIRISH……………………………………………………………… 3 1-BOB Ishlab chiqarish va uni rejalashtirish masalasining umumiy tavsifi ………………. . ……… . ……………………............................. 6 1 .1 Ishlab chiqarishni rejalashtirish va undagi samaradorlik tushunchalari 6 1.2 Ishlab chiqarishni tashkil qilish va rejalashtirish masalalari …...... …... 7 1.3 Chiziqli dasturlash masalasining umumiy qo‘yilishi ............................. 1 1 1.4 Chiziqli dasturlash masalasini yechish uchun simpleks usul …. ……... 2 2 2-BOB Ishlab chiqarishni rejalashtirish va samarali daromad olish masalalari uchun dasturiy ta’minot ………………………………. 27 2 .1 Ishlab chiqarishni samarali rejalashtirish va daromad olish masalalarining matematik modellari ………………………………. 27 2.2 Dasturiy ta’minotdan foydalanuvchilar uchun ko‘rsatmalar ............... 29 2.3 Dasturiy taminotni boshqa mavjud bo‘lgan dasturiy ta‘minotlar bilan taqqoslash ………………………………………………………….. 35 XULOSA…………………………………………………………….. 44 Foydalanilgan adabiyotlar.………………………………………… 45 ILOVALAR 2 Kirish Masalaning qo‘yilishi. Ishlab chiqarishni tashkil etishda samarali reja va daromad olish masalalarini tadqiq qilish va matematik modellari chiziqli dasturlash masalasiga keluvchi ishlab chiqarish masalalari uchun qulay interfeysga ega bo‘lgan dasturiy ta‘minot yaratish. Mavzuning dolzarbligi. Jamiyatning barcha sohalarida ishlab chiqarish va daromad olishni optimallashtirish muhum masala hisoblanadi. Ayniqsa bugungi kunda rivojlanayorgan, shiddat bilan sanoatlashayotgan jamiyatda, tabiiy holda raqobatning kuchayishi ortidan ishlab chiqarishni optimal rejalashtirish va optimal daromad olish eng dolzarb masalalardan biri bo’lib qolmoqda. Ishlab chiqarishni optimallashtirish masalalari nazariy jihatdan, ya’ni ularning matematik va boshqa modellarini yaratish ularni yechish va hakozolar, birmuncha yaxshiroq o’rganilgan bo’lishiga qaramay amaliy jihatda o’rganishga yetarlicha ishlar mavjud bo’lib bulardan biri bu nazariy tomondan yaratilgan modellar uchun dasturiy ta’minot yaratish. Shuning uchun bu ishda ishlab chiqarishni samarali rejalashtirish va daromad olish masalalari uchun dasturiy taminot yaratish masalasi qaraladi. Ishning maqsad va vazifalari. Bitiruv malakaviy ishning asosiy maqsad va vazifasi bu ishlab chiqarish sohalar, ularning turi, yo’nalishi, ishlab chiqarish jarayoni, moddiy ta’minoti va boshqa parametrlariga ko’ra optimal rejalari va daromadlarini hisoblashlarni yengillashtirish. Ilmiy-tatqiqot usullari. Ushbu bitiruv malakaviy ishida ishlab chiqarishni tashkil etishda eng samarali reja va doromad olish masalalarining matematik modeli chiziqli dasturlash masalasiga keladigan hollar uchun o’rganilgan bo’lib bu modelni yechish uchun yaratilgan dasturiy ta’minot simpleks usuliga asoslangan. Mavzuning o‘rganilish darajasi. Yuqorida aytib o’tganimizdek ishlab chiqarishni va daromadni optimallashtirish masalasi nazariy jihatdan ko’plab olimlar tomonida yaxshi o’rganilgan bo’lib ular ushbu masalaning turli xil modellarini yaratish va ularni yechish kabi natijalarni olishgan. Bu kabi natijalar 3 keltirilgan ko’plab adabiyotlar mavzuni tadqiq qilishda o’rganilgan. Mavzuning o’rganilishi boshlang’ch darajada bo’lib, bu mavzuni o’rganish natijasida olingan natija ya’ni yaratilga dasturiy ta’minot sodda bo’lib u faqat bir yo’nalishga mo’ljallangan hisob kitoblarni bajaradi. Bu dasturiy ta’minotni kelajakda yanada mukammallashtirish rejalashtirilgan. Tadqiqotning ilmiy yangiligi. Bitiruv malakaviy ishida olingan natijalar amaliy-uslubiy xarakterga ega bo‘lib, ishda ishlab chiqarishni eng samarali rejalashtirish va daromad olish masalalarini yechishga mo’ljallangan dasturiy ta’minot yaratligan. Bu dasturiy ta’minot PHP dasturlash tilida yaratilgan bo’lib, u vizuallashgan qulay interfeysga ega. Tadqiqot predmeti va ob’ekti. Tadqiqotning predmeti “Jarayonlar tadqiqoti”, “Iqtisodiyotda jarayonlar tadqiqoti”, “Iqtisodiyot masalalarini matematik modellashtirish”, “Matematik dasturlash” , “Java dasturlash tili” va shu kabi fan sohalari bo‘lib, ob’ekti ishlab chiqarishni rejalshtirish masalalarining matematik modellaridan iborat. Tatqiqotnig ilmiy va amaliy ahamiyati. Ishda olingan natijalar va unda qo‘llanilgan usullardan turli iqtisodiy, ijtimoiy sohalarning ko‘pgina amaliy masalalari, jumladan, ishlab chiqarishni rejalashtirish va samarali daromad olish masalalarini tadqiq qilishda, “Jarayonlar tadqiqoti”, “Iqtisoriyotda jarayonlar tadqiqoti”, “Iqtisodiyot masalalarini matematik modellashtirish” va shu kabi fanlarning amaliy mashg‘ulotlari o‘quv jarayonlarida dasturiy vosita sifatida foydalanish mumkin. Ishning tuzilishi. Ushbu ish kirish, ikki bob, xulosa, foydalanilgan adabiyotlar ro‘yxati va ilovalardan iborat. I bob to‘rtta paragrafdan iborat bo‘lib, unda adabyotlardan foydalanilgan holda, bitiruv malakaviy ishiga qo’yilgan “ Ishlab chiqarishni tashkil etishda samarali reja va daromad olish” masalasi ni tavfislash va natija olish uchun zarur bo‘lgan asosiy tushunchalar, ta’riflar, tasdiqlar va matematik modellar keltirilgan. Bularning asosiylari quyidagilardan iborat: Ishlab chiqarishni tashkil qilish va 4 rejalashtirish masalalari va ularning qo’yilishi, Chiziqli dasturlash masalalari va ularning shakllari, Chiziqli dasturlash masalalarini yechish usullari-Simpleks usuli. II bob uchta paragrafdan iborat bo’lib, birinchi paragrafda ishalab chiqarishni tashkil etishda samarali reja va daromad olish masalalarining matematik modellari haqida so’z yuritilgan, ikkinchi paragrafda bu modellardan biri bo‘lgan chiziqli dasturlash masalasini simpleks usuli orqali yechishga asoslangan PHP dasturlash tilida qulay interfeysga ega bo‘lgan dasturiy ta’minotning funksional sxemasi keltirilgan hamda turli masalalarni yechish orqali dasturiy ta’minotdan foydalanuvchilar uchun ko‘rsatmalar berilgan . Uchinchi paragrafda dasturiy ta’minotning to’gri ishlashini tekshirish uchun bir nechta mavjud standartlashgan dasturiy ta’minotlar bilan taqqoslashlar o’tkazilgan. Olingan natijalarning qisqacha mazmuni. Bitiruv malakaviy ishida ishalab chiqarishni samarali rejalashtirish masalalari va ularni yechish uchun olingan matematik modellar bilan tanishib chiqildi hamda bu modellardan biri bo’lgan chiziqli dasturlash masalasini simpleks usuli yordamida yechishga asoslangan dasturiy ta’minot yaratildi. Bu dasturiy ta’minotdan foydalanib, turli xil cheklanmalar orgali berilgan chiziqli dasturlash masalalarini yechish mumkin, qaysiki bu masalalar ishlab chiqarishni rejalashtirish va samarali daromad olish masalalarining asosiy matematik modellaridan biri hisoblanadi. Chiziqli dasturlash masalasi simpleks usuliga asoslanib yechiladi. Dasturiy ta’minot yordamida olingan chiziqli dasturlash masalasining yechimi ishlab chiqarishni optimal rejalashtirish va optimal daromad olishning yechimi bo’ladi, ya’ni maqsad funksiyasining maksimumi optimal daromad olishga va shu funksiyani maksimumga erishtiruvchi o’zgaruvchilarning qiymati optimal rejalarga mos keladi. 5 I -BOB Ishlab chiqarish va uni rejalashtirish masalasining umumiy tavsifi 1.1. Ishlab chiqarishni rejalshtirish va samaradorlik tushunchalari. Ishab chiqarishni rejalashtirish bu kelajakda ishlab ishlab chiqish uchun tuzilgan reja bo’lib unda barcha kerakli narsalar oldindan aniqlanadi va taqsimlanadi. Ishlab chiqarishni rejalashtirish bu kompaniya yoki sanoatda ishlab chiqarishning rejasini tuzish demakdir. Talabgorlarga xizmat ko’rsatish uchun ishlab chiqarishni rejalashtirishda ishchi kuchi, mahsulot, ishlab chiqarish hajmi kabi zaxiralarni taqsimlashdan fydalaniladi. Har hil ishlab chiqarish turlari mavjud bo’lib buladga bir xil turdagi mahsulot ishlab chiqarishni, har xil turdagi mahsulot ishlab chiqarishni, uzluksiz ishlab chiqarish, ya’ni biror turdagi standartlashgan mahsulotni uzoq muddatli ishlab chiqarishni va boshqa shu kabilarni misol qilishimiz mumkin. Bu ishlab chiqarishlarning har birining o’ziga hos ishalb chiqarish rejalari mavjud. Ishlab chiqarishni rejalashtirish uni shu rejaga ko’ra nazorat qilish masalalasi bilan birga qaraladi. Ishlab chiqarish masalalari sof hayotiy masalalar bo’lib bu masalalarni yechish nazariy jihatdan ko’plab olimlar tomonidan o’rganilgan va ularning natijalari ushbu adabyotlarda keltirilgan (qarang: [1], [3], [4], [6], [7], [8], [9] ). Bu masalalar uchun turli xil modellar yaratilgan va ularni yechish uchun bir qancha usullar keltirilgan. Ishlab chiqarishni tashkil etish masalalarini yechishning umumiy bir metod yoki modellar mavjud bo’lmay masalalrning turiga qarab ularni yechishning ko’plab usullari ular uchun modellar mavjud masalan, ishlab chiqarishni tashkil etish, rejalashtirish va samarali daromadga ega bo’lishning soddaroq masalalarining asosiy qismining matematik modeli chiziqli dasturlash masalasiga keladi, murakkabroq maslalari ya’ni ko’p tarmoqli, takrorlanuvchi va boshq ko’plab parametrga ega bo’lgan masalalrining matematik modeli dinamik dasturlash, qavariq dasturlash va boshqa dasturlash masalalariga hamda modellarga keladi. Quyida biz ishlab chiqarishni rejalashtirish va samarali daromad olish masalalarini yaxshiroq tushunish uchun oddiy misollar qaraymiz. Korxona bolalar uchun 2 turdagi (A va B) o’yinchoq ishlab chiqaradi. Har bir B o’yinchoqni ishlab chiqish A o’yinchoqni ishlab chiqishga nisbatan 2 marta 6 ko’p vaqt talab qiladi va korxonaning o’yinchoq ishlab chiqarish uchun kunlik vaqti maksimumi 2000 dona o’yinchoq ishlab chiqarishga etadi. Xomashyo (plastik) zaxirasi bir kunda 1500 ta o’yinchoq ishlab chiqarishga yetadi. B o’yinchoqni qo’shimcha bezash uchun kunlik 600 tasiga yetadigan xomashyo bor. Agar korxona A o’yinchoqdan 3 so’m va B o’yinchoqdan 5 so’mdan foyda olsa, bir kunda nechta qo’g’irchoq ishlab chiqish kerak?( maksimal foyda olish uchun). Endi bu masalani yechish uchun uning matematik modelini tuzamiz. X1 va X2 bilan , mos ravishda bir kunda ishlab chiqariladigan A va B o’yinchoq lar sonini belgilaymiz. A qo’g’irchoqni ishlab chiqarish uchun t soat vaqt talab qilinsin, u holda B qo’g’irchoqni ishlab chiqarish uchun 2t vaqt kerak bo’ladi. Demak X1 va X2 o’yinchoq larni ishlab chiqarish 2000t soatdan oshmasligi kerak. Shuning uchun tX1+2tX2<=2000t. Xomashyo zaxirasini etiborga olib, X1+X2<=1500 shartni olamiz va ikkinchi o’yinchoq uchun qo’shimcha xomashyo miqdorini e’tiborga olib X2<=600 ni hosil qilamiz. Bundan tashqari o’yinchoqlar soni nomanfiy va umumiy foyda 3X1+5X2 ko’rinishda bo’ladi. Demak masalaning matematik modeli quyidagicha: Max: Y=3X1+5X2 X1+2X2<=2000 X1+X2<=1500 X2<=600 X1>=0, X2>=0. 1.2. Ishlab chiqarishni tashkil qilish va rejalashtirish masalasi . Ishlab chiqarishni optimal rejalashtirish va samarali daromad olish masalalarini yaxshiroq tushinish uchun bu paragrafda sodda misollar qaraymiz. Faraz qilaylik, korxonada m xil mahsulot ishlab chiqarilsin: ulardan ixtiyoriy birini i(i=1,2 ,… ,m) bilan belgilaymiz. Bu mahsulotlarni ishlab chiqarish uchun n xil ishlab chiqarish faktorlari zarur bo’lsin. Ulardan ixtiyoriy birini j(j=1,2 ,… ,n) bilan belgilaymiz. 1. Har bir ishlab chiqarish faktorining zaxirasi va ularning bir birlik mahsulotni 7 ishlab chiqarish uchun sarf qilinadigan me’yori quyidagi jadvalda berilgan: i/ch faktorlari i/ch mahsulot turlari1 2 3 … n Mahsulot birligidan olinadigan daromad 1 a11 a12 a13 … a1n C1 2 a21 a22 a23 … a2n C2 … … … … … … … m am1 am2 am3 … amn Cm i / ch faktorining zaxirasi b1 b2 b3 … bn 2. Jadvaldagi har bir bj – j -ishlab chiqarish faktorining zaxirasini; ai – i - mahsulotning bir birligini ishlab chiqarish uchun sarf qilinadigan j - faktorning me’yori; Ci – korxonaning i -mahsulot birligini realizatsiya qilishdan oladigan daromadini bildiradi. 3. Masalaning iqtisodiy ma’nosi: korxonaning ishlab chiqarish rejasini shunday tuzish kerakki: a) hamma mahsulotlarni ishlab chiqarish uchun sarf qilinadigan har bir ishlab chiqarish faktorining miqdori ularning zaxirasidan oshmasin; b) mahsulotlarni realizatsiya qilishidan korxonananing oladigan daromadi maksimal bo’lsin. 4. Rejalashtirilgan davr ichida ishlab chiqariladigan i -mahsulotining miqdorini xi bilan belgilaymiz. U holda masaladagi a) shart quyidagi tengsizliklar sistemasi orqali ifodalanadi: { a11x1+a21x2+...+am1xm≤b1, a12x1+a22x2+...+am2xm≤b2, ..................................................., a1nx1+a2nx2+...+amnxm≤bn. 5. Masalaning iqtisodiy ma’nosiga ko’ra hamma noma’lumlar manfiy bo’lmasligi kerak, ya’ni: xi≥ 0,(i= 1,2 ,… ,m ) 6. Masaladagi b) shart uning maqsadini aniqlaydi. Demak masalaning maqsadi 8 mahsulotlarni realizatsiya qilishdan korxonaning oladigan umumiy daromadini maksimallashtirishdan iborat va uniY = c1x1+c2x2+...+cmxm→ max ko’rinishdi ifodalash mumkin. Shunday qilib, ishlab chiqarishni rejalashtirish masalasining matematik modeli quyidagi ko’rinishda bo’ladi. { a11x1+a21x2+...+am1xm≤b1, a12x1+a22x2+...+am2xm≤b2, ..................................................., a1nx1+a2nx2+...+amnxm≤bn, x1≥ 0, x2≥ 0,… , xm≥ 0, Y = c1x1+c2x2+...+cmxm→ max Bu esa chiziqli dasturlash masalasi bo’lib bu masalni yechishning bir nechta usullari mavjud bular simpleks, ikki yoqli simpleks, grafik usullari va boshqa usullardir. Quyidagi ikkinchi masala ham huddi yuqoridagiga o’xshab ishlab chiqarishni rejalashtirish talab etiladi. Endi ushbu masalani qaraymiz. Faraz qilaylik farmasevtika fabrikasi 2 turdagi (A va B) dori ishlab chiqarishni rejalashtirgan. Bu dorilar bir hil shisha idishchalarda ishlab chiqariladi. Fabrikaning xomashyosi A dori uchun 20000 ta shisha idishchaga yetadi B dori uchun 40000 ta ammo barcha idishchalarning soni 45000 ta. 1000 shisha idishcha A doridan ishlab chiqish uchun 3 soat vaq ketadi, B doridan shuncha miqdorda ishlab chiqish uchun 1 soat vaqt ketadi. A va B dorilardan ishlab chiqish uchun fabrikaning ixtiyorida 66 soat mavjud. A dorining har bir shishasidan 8 so’m B dorinikidan esa 7 so’m foyda qoladi. Maksimal foyda olish uchun fabrikaning ishlab chiqish rejasi qanday bo’lishi kerak. Bu masalani yechish uchun matematik modelni quyidagicha tuzamiz. A doridan 1000 shisha ishlab chiqishni X1 orqali belgilaymiz va huddi shunday X2 orqali B doridan 1000 ta ishlab chiqishni belgilaymiz.A doridan 1000 shisha ishlab chiqarish uchun 3 soat vaqt talab qilingani uchun har 1000 ta dori uchun 3X1 vaqt ketadi xuddi shunday har 1000 ta B dori uchun X2 vaqt ketadi. Ikkala dorining har 1000 tasini ishlab chiqish uchun 3X1+X2 vaqt ketadi. Fabrikada dori ishlab 9 chiqish uchun 66 soat vaqt bo’lgani uchun ikkita doridan ishlab chiqish uchun ketgan vaqt 66 dan oshmasligi kerak, ya’ni 3X1+X2<=66. Barcha idishalr soni 45000 ta bo’gani uchun hamma ishlab chiqilgan A va B dorilar soni idishlar sonidan oshmaydi, ya’ni X1+X2<=45. A dorini ishlab chiqish uchun xomaysho 20000 idishga va B dorini ishlab chiqich uchun xomashyo 40000 idishga yetishini etiborga olib ushbu shartlarni olamiz X1<=20 va X2<=40. A dorining har bir shishasi uchun foydaning 8 so’mligina va B dori uchun 7 so’mligini etiborga olsak, u holda umumiy foyda 8000X1+7000X2 ko’rinishda bo’ladi va yana shisha idishlar soni nomanfiyligini etiborga olsak, X1>=0 va X2>=0 ga ega bo’lamiz. Shunday qilib berilgan masalaning matematik modeli quydagicha ekan: Max: Y=8000X1+7000X2 3X1+X2<=66 X1+X2<=45 X1<=20 X2<=40 X1>=0, X2>=0. Demak masalning matematik modeli 2 ta o’zgaruvchi (X1 va X2) va 4 ta chegaraviy shartlar (cheklanmalar)dan iborat bo’lgan chiziqli dasturlash masalasiga keldi. Firma ishlab chiqaradigan A,B,C tipdagi mahsulotlar uchun α , β , γ texnologik operasiyalardan foydalaniladi. α operasiyaning A,B,C tipdagi mahsulotlar birligini tayyorlash uchun zarur vaqti mos ravishda 2 minut, 1 minut, 2 minutni hamda bu operasiyaning sutkalik vaqt zaxirasi 450 minutni tashkil etadi. β operasiya uchun bu miqdorlar 1, 2, 3, 470ga, γ operasiya uchun esa 3, 2, 1, 430ga teng. Agar A,B,C tipdagi mahsulotlarning 1 birligini sotishdan olinadigan foyda mos ravishda 40, 50, 30 pul birligini tashkil etsa, firma uchun eng ma’qul ishlab chiqarish rejasini aniqlash talab etiladi. 10 1.3. Chiziqli dasturlash masalasining umumiy quyilishi Yuqorida aytib o’tganimizdek chiziqli dasturlash masalasi ishlab chiqarishni tashkillashtirish va samarali daromad masalalrining asosiy matematik modellaridan biri bo’lgani va biz yaratgan dasturiy ta’minot chiziqli dasturlash masalasini yechishga qaratilganligi uchun biz bu paragrafda chiziqli dasturlash masalasining asosiy tushunchalarini keltiramiz. Chiziqli dasturlash masalasi umumiy holda quyidagicha ifodalanadi:{ a11x1+a12x2+...+a1nxn≥(≤)b1, a21x1+a22x2+...+a2nxn≥(≤)b2, ..............................................., am1x1+am2x2+...+amn xn≥(≤)bm, (1) x1≥ 0,x2≥ 0,...,xm≥ 0, (2) Y = c1x1+c2x2+⋯ +cmxm→ min (max ) (3) (1) va (2) shartlarni qanoatlantiruvchi noma’lumlarning shunday qiymatlarini topish kerakki, ular (3) chiziqli funksiyaga minimal (maksimal) qiymat bersin. Masalaning (1) va (2) cheklamalari uning chegaraviy shartlari deb, (3) chiziqli funksiya esa masalaning maqsadi yoki maqsad funksiyasi deb ataladi. Masaladagi barcha cheklamalar shartlar va maqsad funksiya chiziqli ekanligi ko’rinib turibdi. Shuning uchun ham (1)–(3) masala chiziqli dasturlash masalasi deb ataladi. Konkret masalalarda (1) shart tenglamalar sistemasidan, « ¿ » yoki « ¿ » ko’rinishdagi tengsizliklar sistemasidan yoki aralash sistemadan iborat bo’lishi mumkin. Lekin ko’rsatish mumkinki, (1)–(3) ko’rinishdagi masalani osonlik bilan quyidagi ko’rinishga keltirish mumkin: { a11x1+a12x2+...+a1nxn=b1, a21x1+a22x2+...+a2nxn=b2, ..............................................., am1x1+am2x2+...+amn xn=bm, (4) x1≥0,x2≥ 0,...,xn≥0, (5) 11 Y = c1x1+c2x2+⋯ +cnxn→ min(6) (4)–(6) ko’rinish chiziqli dasturlash masalasining kanonik ko’rinishi deb ataladi. Bu masala vektorlar yordamida quyidagicha ifodalanadi: P1x1+P2x2+⋯ +Pnxn= P0 (7) X≥0, (8) Y = C TX → min (9) bu yerda P1= ( a11 a21 ... am1 ) , P2= ( a12 a22 ... am2 ) ,...,Pn= ( a1n a2n ... amn ) , P0= ( b1 b2 ... bm ) , CT=(c1,c2,… ,cn) – vektor - qator. X =(x1,x2,… ,xn) – vektor - ustun. (4) – (6) masalaning matritsa ko’rinishdagi ifodasi quyidagicha tuziladi: AX = P0 (10) X≥0, (11) Y = C TX → min (12) bu yerda CT=(c1,c2,… ,cn) – qator vektor, A= (aij) – (4) sistema koeffitsiyentlaridan tashkil topgan matritsa; X =(x1,x2,… ,xn) va P0=(b1,b2,… ,bn) – ustun vektorlar. (1. 17) – (1. 19) masalani yigindilar yordamida ham ifodalash mumkin: ∑ j=1 n aij= bi, ( i=1,2 ,… ,m ) (13) xj≥0, ( j=1,2 ,… ,n ) (14) Y = ∑ j=1 n cjxj→ min (15) 1-ta’rif . Berilgan (4) – (6) masalaning joiz yechimi yoki rejasi deb, uning (4) va (6) shartlarini qanoatlantiruvchi X =(x1,x2,… ,xn) vektorga aytiladi. 2-ta’rif. Agar joiz rejalar to’plamiga tegishli bo’lgan X0 vektorning n−m 12 ta koordinatasi (n – noma’lumlar soni, m – tenglamalar soni) nolga teng bo’lib, qolgan m ta koordinatalariga mos kelgan shart vektorlar(masalan, Pn+1 , Pn+2, ..., Pn+m vektorlar) chiziqli erkli bo’lsa, u holda X0 joiz reja basis (asosiy) reja deyiladi. 3-ta’rif. Agar X =(x1,x2,… ,xn) bazis rejadagi musbat koordinatalar soni m ga teng bo’lsa, u holda bu reja aynimagan bazis reja, aks holda aynigan bazis reja deyiladi. 4-ta’rif. Chiziqli funksiya (6) ga eng kichik qiymat beruvchi X =(x1,x2,… ,xn) bazis reja masalaning optimal rejasi yoki optimal yechimi deyiladi. Chiziqli dasturlash masalasi ustida quyidagi teng kuchli almashtirishlarni bajarish mumkin. 1. max Y ni min Y ga aylantirish. Har qanday chiziqli dasturlash masalasini kanonik ko’rinishga keltirish uchun (1) tengsizliklar sistemasini tenglamalar sistemasiga va max Y ni min Y ga aylantirish kerak. max Y ni min Y ga keltirish uchun, max Y ni qarama-qarshi ishora bilan olish, ya’ni − max Y= min Y yoki aksincha max Y=− min Y ko’rinishda olish yetarlidir. Haqiqatan ham, har qanday f(x1,x2,… ,xn) funksiyaning minimumi qarama-qarshi ishora bilan olingan shu funksiya maksimumining qiymatiga teng, ya’ni min f(x1,x2,… ,xn) va − max [f(x1,x2,… ,xn)] , max f(x1,x2,… ,xn) va −min [f(x1,x2,… ,xn)] ifodalar noma’lumlarning bir xil qiymatlaridagina o’zaro teng bo’lishini ko’rsatish mumkin. 2. Tengsizliklarni tenglamaga aylantirish. n noma’lumli a1x1+a2x2+...+anxn≤ b (16) chiziqli tengsizlikni qaraymiz. Bu tengsizlikni tenglamaga aylantirish uchun uning kichik tomoniga nomanfiy o’zgaruvchini, ya’ni xn+1≥0 ni qo’shamiz. 13 Natijada n+1 noma’lumli chiziqli tenglamaga ega bo’lamiz: a1x1+a2x2+...+anxn+xn+1= b (17) (16) tengsizlikni tenlamaga aylantirish uchun qo’shilgan xn+1 o’zgaruvchi qo’ shimcha o’zgaruvchi deb ataladi. (16) tengsizlik va (17) tenglamaning yechimlari bir xil ekanligi quyidagi teoremada ko’rsatilgan. 1-teorema. Berilgan (16) tengsizlikning har bir X =(α1,α2,… ,αn) yechimiga (17) tenglamaning faqat bitta Y0= (α1,α2,… ,αn,αn+1) yechimi mos keladi va aksincha, (17) tenglamaning har bir Y0 yechimiga (16) tengsizlikning faqat bitta X0 yechimi mos keladi. Teorema isboti. Faraz qilaylik, X0 (16) tengsizlikning yechimi bo’lsin. U holda a1α1+a2α2+… +anαn≤ b munosabat o’rinli bo’ladi. Tengsizlikning chap tomonini o’ng tomonga o’tkazib hosil bo’lgan ifodani αn+1 bilan belgilaymiz 0≤ b− (a1α1+a2α2+… +anαn)= αn+1. Endi Y0= (α1,α2,… ,αn,αn+1) vektorni (17) tenglamaning yechimi ekanligini ko’rsatamiz. a 1α 1+ a 2α 2+ … + a nα n+ α n+1= a1α1+ a 2α 2+ … + a nα n+ + (b − a1α 1− a2α 2− … − a nα n)= b Endi agar Y0 (17) tenglamani qanoatlantirsa, u holda u (16) tengsizlikni ham qanoatlantirishini ko’rsatamiz. Shartga ko’ra: a1α1+a2α2+… +anαn+αn+1= b ,αn+1≥ 0. Bu tenglamadan αn+1≥ 0 sonni tashlab yuborish natijasida a1α1+ a2α2+… + anαn≤ b ,αn+1≥ 0 tengsizlikni hosil qilamiz. Bundan ko’rinadiki, X =(α1,α2,… ,αn)T – (16) tengsizlikning yechimi ekan. 14 Shunday yo‘l bilan chiziqli dasturlash masalasining cheklamalaridagi tengsizliklarni tenglamalarga aylantirish mumkin. Bunda shunga e’tibor berish kerakki, sistemadagi turli tengsizliklarni tenglamalarga aylantirish uchun ularga bir-birlaridan farq qiluvchi nomanfiy o’zgaruvchilarni qo’shish kerak. Masalan, agar chiziqli dasturlash masalasi quyidagi{ a11x1+a12x2+...+a1nxn≤b1, a21x1+a22x2+...+a2nxn≤b2, ............................................., am1x1+am2x2+...+amn xn≤bm, (18) x1≥0,x2≥ 0,...,xn≥0, (19) Y = c1x1+c2x2+⋯ +cnxn→ max (20) ko’rinishda bo’lsa, bu masaladagi tengsizliklarning kichik tomoniga xn+1≥ 0 , xn+2≥ 0 , ..., xn+m≥ 0 qo’shimcha o’zgaruvchilar qo’shish yordamida tenglamalarga aylantirish mumkin. Bu o’zgaruvchilar Y= CTX ga 0 koeffitsiyent bilan kiritiladi. Natijada berilgan (18) – (20) masala quyidagi ko’rinishga keladi. { a11x1+a12x2+...+a1nxn+xn+1=b1, a21x1+a22x2+...+a2nxn+xn+2=b2, .........................................................., am1x1+am2x2+...+amn xn+xn+m=bm, (21) x1≥ 0,x2≥ 0,...,xn≥ 0,… ,xn+m≥ 0 (22) Y = c1x1+c2x2+⋯ +cnxn+0(xn+1+⋯ + xn+m)→ max (23) Xuddi shuningdek, { a11x1+a12x2+...+a1nxn≥b1, a21x1+a22x2+...+a2nxn≥b2, ............................................., am1x1+am2x2+...+amn xn≥bm, (24) x1≥0,x2≥ 0,...,xn≥0, (24) Y = c1x1+c2x2+⋯ +cnxn→ min (25) ko’rinishda berilgan chiziqli dasturlash masalasini kanonik ko’rinishga keltirish mumkin. Buning uchun qo’shimcha xn+1≥ 0 , xn+2≥ 0 , ..., xn+m≥ 0 o’zgaruvchilar 15 tengsizliklarning katta tomonidan ayriladi. Natijada quyidagi masala hosil bo’ladi:{ a11x1+a12x2+...+a1nxn−xn+1=b1, a21x1+a22x2+...+a2nxn−xn+2=b2, .........................................................., am1x1+am2x2+...+amn xn−xn+m=bm, (26) x1≥ 0,x2≥ 0,...,xn≥ 0,… ,xn+m≥ 0 (27) Y = c1x1+c2x2+⋯ +cnxn+0(xn+1+⋯ + xn+m)→ min (28) Endi chiziqli dasturlash masalasi yechimlarining xossalari bilan tanishamiz. Buning uchun eng avval qavariq kombinatsiya va qavariq to’plam tushunchasini eslatib o’tamiz. 5-ta’rif. A1,A2,… ,An vektorlarning qavariq kombinatsiyasi deb αi≥ 0, ∑ i=1 n αi= 1, i= 1,n shartlarni qanoatlantiruvchi A= α1A1+α2A2+⋯ +αnAn vektorga aytiladi. n− o’lchovli fazodagi har bir A= (a1,a2,… ,an) vektorga koordinatalari (a1,a2,… ,an) bo’lgan nuqta mos keladi. Shuning uchun bundan keyin A= (a1,a2,… ,an) vektorni n− o’lchovli fazodagi nuqta deb qaraymiz. 6-ta’rif. Agar n− o’lchovli vektor fazodagi C to’plam o’zining ixtiyoriy A1 va A2 nuqtalari bilan bir qatorda bu nuqtalarning qavariq kombinatsiyasidan iborat bo’lgan A= α1A1+α2A2 ( α1>0 , α1>0 , α1+α2= 1 ) nuqtani ham o’z ichiga olsa, ya’ni A1,A2∈C ⇒ A∈C bo’lsa, bu to’plam qavariq to’plam deb ataladi. 2-teorema. Chiziqli dasturlash masalasining mumkin bo’lgan rejalaridan tashkil topgan to’plam qavariq to’plam bo’ladi. Isboti. Chiziqli dasturlash masalasining ixtiyoriy ikkita mumkin bo’lgan rejasining qavariq kombinatsiyasi ham reja ekanligini ko’rsatamiz. Faraz qilaylik, X1 va X2 berilgan chiziqli dasturlash masalasining mumkin bo’lgan rejalari 16 bo’lsin. U holdaAX 1= P0, X1≥ 0 (29) va AX 2= P0, X 2≥ 0 (30) munosabatlar o’rinli bo’ladi. Endi x1 va x2 rejalarning qavariq kombinatsiyasini tuzamiz. X = αx 1+(1− α)x2, 0≤ α≤ 1 hamda uni reja ekanligini ko’rsatamiz: AX = A[αx 1+(1− α)x2]= α Ax 1+(1− α)Ax 2. Endi (29) va (30) tenglamalarni inobatga olib topamiz: AX = αP 0+(1− α)P0= P0. Bu munosabat X vektor ham reja ekanligini ko’rsatadi. 3-teorema. Chiziqli dasturlash masalasining maqsad funksiyasi uzining optimal qiymatiga shu masalaning rejalaridan tashkil topgan qavariq to’plamning burchak nuqtasida erishadi. Agar chiziqli funksiya K qavariq to’plamning birdan ortiq burchak nuqtasida optimal qiymatga erishsa, u shu nuqtalarning qavariq kombinatsiyasidan iborat bo’lgan ixtiyoriy nuqtada ham o’zining optimal qiymatiga erishadi. Isboti. Deylik, X0 nuqta chiziqli funksiyaga ekstremum qiymat beruvchi nuqta bo’lsin. Agar X0 nuqta burchak nuqta bo’lsa, u holda teorema o’z-o’zidan isbot qilingan bo’ladi. Faraz qilaylik, X0 nuqta K qavariq to’plamning ichki nuqtasi, x1,x2,… ,xp , nuqtalar esa uning burchak nuqtalari bo’lsin (1.1-shakl): 17 X0 nuqta chiziqli funksiyaga minimum qiymat beruvchi nuqta bo ’ lganligi sababli Y(X 0)≤Y(X ) tengsizlik ixtiyoriy X ∈ K uchun o’rinli bo’ladi. X0 nuqta ichki nuqta bo’lganligi uchun uni burchak nuqtalarning qavariq kombinatsiyasi orqali ifodalash mumkin: X0= ∑ i=1 p αiXi, ∑ i=1 p αi= 1, αi≥ 0,(i= 1,...,p) (31) Y(X) chiziqli funksional bo’lganligi sababli Y (X 0)= Y (∑ i=1 p αiX i)= ∑ i=1 p αiY (X i)= m (32) bu yerda m har qanday X ∈ K uchun funksiyaning minimal qiymati. (32) tenglikdagi har bir Y(X) ni min Y(X i)= Y(X m) bilan almashtirib quyidagi tengsizlikni hosil qilamiz: Y(X 0)≥ ∑ i=1 p αiY(X m)= Y (X m)∑ i=1 p αi= Y(X m), ya’ni Y(X0)≥Y (X m). Bu tengsizlikni (32) tenglik bilan solishtirib quyidagiga ega bo’lamiz Y(X 0)= Y (X m)= m . Demak, Xm burchak nuqtada chiziqli funksiya uzining minimal qiymatiga 18 erishar ekan. Endi maqsad funksiya o’zining minimal qiymatiga X1,X2,… ,X p nuqtalarda erishsin, ya’ni Y (X 1)= Y (X 2)= ⋯ = Y (X p)= m shart o’rinli bo’lsin deb faraz qilamiz. Bu nuqtalarning qavariq kombinatsiyasidan iborat bo’lgan X nuqtani qaraymiz. X = ∑ i=1 p αiX i, αi≥ 0, (i= 1,...,p) ∑ i=1 p αi= 1. U holda Y(X 0)= Y (∑ i=1 p αiX i)= ∑ i=1 p αiY(X i)= m . Demak, maqsad funksiya X nuqtada ham minimum qiymatga erishar ekan. Shu bilan teorema isbot qilindi. 4-teorema . Agar k ta o’zaro chiziqli bog’liq bo’lmagan P1,P2,… ,Pk vektorlar berilgan bo’lib, ular uchun P1x1+ P2x2+⋯ + Pkxk= P0 (33) tenglik barcha xi>0 lar uchun o’rinli bo’lsa, u holda X=(X1,X2,… ,X k,0… 0) vektor K qavariq to’plamning burchak nuqtasi bo’ladi. Isboti. Ma’lumki (33) tenglikni qanoatlantiruvchi nomanfiy koordinatali X=(x1,x2,… ,xk) vektor chiziqli dasturlash masalasining rejasi bo’ladi. Deylik X burchak nuqta bo’lmasin. U holda X rejani X1 va X2 burchak nuqtalarning qavariq kombinatsiyasi orqali ifodalash mumkin, ya’ni X = α1X1+(1− α1)X2 0≤ α1≤ 1 X vektorning n− k ta komponentasi nolga teng bo’lib, X1 va X2 vektorlarning koordinatalari musbat va 0≤ α1≤ 1 tengsizlik o’rinli bo’lganligi sababli X1 va X2 19 vektorlarning ham n-k ta koordinatasi noldan iborat bo’ladi, ya’niX1=(x1 (1),x2 (1),...,xk (1),0,0 ,...,0), X2=(x1 (2),x2 (2),...,xk (2),0,0 ,...,0) X1 va X2 vektorlar chiziqli dasturlash masalasining rejalari, shuning uchun AX 1= P0 AX 2= P0 tengliklar o’rinli bo’ladi. Bu shartlarni quyidagi formada tuzamiz: P1x1 (1)+ P2x2 (1)+⋯ + Pkxk (1)= P0, P1x1 (2)+ P2x2 (2)+⋯ + Pkxk (2)= P0. Ma’lumki, P0 vektorning o’zaro chiziqli bog’liq bo’lmagan P1,P2,… ,Pk vektorlar orqali faqat bitta yoyilmasini topish mumkin. Sh.uning uchun X = X i (1)= X i (2) Demak, X vektorni K to’plamning ixtiyoriy ikkita nuqtasining qavariq kombinatsiyasi orqali ifodalash mumkin emas ekan. Bundan X nuqta K to’plamning burchak nuqtasi bo’ladi degan xulosa kelib chikadi. Shu bilan teorema isbot qilindi. 5-teorema . Agar X=(x1,x2,… ,xn) burchak nuqta bo’lsa, u holda musbat xi larga mos keluvchi vektorlar o’zaro chiziqli erkli vektorlar sistemasini tashkil qiladi Quyidagi kanonik ko’rinishda yozilgan chiziqli dasturlash masalasini qaraymiz. { a11 x1+a12 x2+...+a1nxn= b1, a21 x1+a22 x2+...+a2nxn= b2, −− −−−−−−−− −−−−− am1x1+am2x2+...+amn xn= bm, (1) x1≥ 0,x2≥ 0,...,xn≥ 0, (2) Y = c1x1+c2x2+...+cnxn→ min (3) Faraz qilaylik, kanonik ko’rinishdagi (1) – (3) chiziqli dasturlash 20 masalasining optimal yechimini topish kerak bo’lsin. Masalaning optimal yechimi uning bazis yechimlaridan biri bo’lib, unda (3) maqsad funksiya minimal qiymatga erishadi. Demak, optimal yechimni bazis yechimlar ichidan qidirish kerak. Faraz qilaylik, (1) sistema x1,x2,...,xm bazis o’zgaruvchilarga nisbatan aniqlangan quyidagi ko’rinishga keltirilgan bo’lsin: { x1=b10+b11xm+1+b12xm+2+...+b1n−mxn, x2= b20+b21xm+1+b22xm+2+...+b2n−mxn, ........................................................... xm=bm0+bm1xm+1+bm2xm+2+...+bmn−mxn, (4) Bu sistema x -tenglamalar sistemasi deyiladi. Bu sistemadan foydalanib, (3) maqsad funksiyani erkli o’zgaruvchilarning funksiyasi, ya’ni Y= c00+ ∑ j=1 n−m c0jxm+j (5) ko’rinishida ifodalash mumkin. (4) ifodadagi erkli o’zgaruvchilarni 0 ga tenglab, x1=b 10 , x2=b 20,...,xm=b m0 bazis yechimni topamiz. Bu bazis yechimdagi (5) maqsad funksiyaning qiymati Y= c00 bo’ladi. Topilgan bazis yechimni optimal yechim bo’lishini tekshirish hamda, agar bu bazis yechim optimal yechim bo’lmasa, boshqa bazis yechimga o’tish qoidasi bilan tanishish uchun (4) sistemani va (5) funksiyani quyidagi ko’rinishdagi jadvalga joylashtiramiz. Bazis o'zgaruvchi B0 Erkli o'zgaruvchilar xm+1 xm+2 … xm+s … xn x1 b10 b11 b12 … b1s b1n−m x2 b20 b21 b22 … b2s b2n−m … … … … … … … … xk bk0 bk1 bk2 … bks bkn−m … … … ... … … … … xm bm0 bm1 bm2 … bms … Bmn−m Y C00 C01 C02 … C0s C0n−m 21 Bunday jadval simpleks* jadval deb ataladi. Simpleks jadvalning bir necha turlari mavjud bo’lib, ularning ba’zilari bilan keyingi bandlarda tanishamiz. Agar B0 vektorning barcha elementlari uchun bi0>0 (i=1,...,m) shart o’rinli bo’lsa, u holda X0=(b10,b20 ,...,bm0,0,0 ,...,0) vektor berilgan masalaning bazis rejalaridan biri bo’ladi. Bu rejaga maqsad funksiyaning Y(X 0)= c00 qiymati mos keladi. Agar (5) yoyilmadagi c01,c02,...,c0n−m, elementlarning barchasi nomanfiy bo’lsa, ya’ni c0j≥ 0 (j=1,2 ,...,n−m) shart o’rinli bo’lsa, u holda topilgan X0 bazis reja optimal reja bo’ladi. Optimal rejadagi maqsad funksiyaning eng kichik qiymati Ymin = Y (X 0)= c00 bo’ladi. 1.4. Chiziqli dasturlash masalasini yechish uchun simpleks usul Dansig yaratgan simpleks usul har bir tenglamada bittadan ajratilgan no’malum (bazis o’zgaruvchi) qatnashishi shartiga asoslangan. Boshqacha aytganda, ChD masalasida m ta o’zaro chiziqli erkli vektorlar mavjud deb qaraladi. Umumiylikni buzmagan holda bu vektorlar birinchi m ta P1,P2,...,Pm vektorlardan iborat bo’lsin, deylik. U holda masala quyidagi ko’rinishda bo’ladi: { x1+a1m+1xm+1+...+a1nxn= b1, x2+a2m+1xm+1+...+a2nxn= b2, −− −−−−−−−− −−−−−− xn+amm +1xm+1+...+amn xn= bm, (6) x1≥ 0 ,x2≥ 0,...,xn≥ 0, (7) Y = c1x1+c2x2+...+cnxn→ min, (8) (6) sistemani vektor shaklida yozib olaylik: 22 P1x1+P2x2+...+Pmxm+Pm+1xm+1+...+Pnxn= P0(9) Bu yerda P1= ( 1 0 ... 0 ) , P2= ( 0 1 ... 0 ) , …, Pm= ( 0 0 ... 1 ) , Pm+1= ( a1m+1 a2m+1 ... amn +1 ) , …, Pn= ( a1n a2n ... amn ) , P0= ( b1 b2 ... bm ) , P1,P2,...,Pm vektorlar sistemasi m -o’lchovli fazoda o’zaro chiziqli erkli bo’lgan birlik vektorlar sistemasidan iborat. Ular m o’lchovli fazoning bazisini tashkil qiladi. Ushbu vektorlarga mos keluvchi x1,x2,...,xm o’zgaruvchilarni «bazis o’zgaruvchilar» deb ataladi. xm+1,xm+2,...,xn – bazis bo’lmagan (erkli) o’zgaruvchilar. Agar erkli o’zgaruvchilarga 0 qiymat bersak, bazis o’zgaruvchilar ozod hadlarga teng bo’ladi. Natijada X0=(b1,b2,...,bm,0,...,0) yechim hosil bo’ladi. Bu yechim boshlang’ich joiz yechim bo’ladi. Ushbu yechimga x1P1+x 2P2+⋯ +x mPm = P 0 yoyilma mos keladi. Bu yoyilmadagi P1, P 2, ..., P m vektorlar o’zaro erkli bo’lganligi sababli topilgan joiz yechim bazis yechim bo’ladi. Dansig usulida simpleks jadval quyidagi ko’rinishda bo’ladi: Bazis vekt. Cbaz P0 c1 c2 … cm cm+1 … ck … cn P1 P2 … Pm Pm+1 … Pk … Pn P1 c1 b1 1 0 ... 0 a1m+1 ... a1k ... ... a1n P2 c2 b2 0 1 ... 0 a2m+1 ... a2k ... a2n … P1 … c1 … b1 … 0 ... 0 ... ... 0 ... a1m+1 ... ... a1k ... ... ... a1n … Pm … cm … bm … 0 ... 0 ... ... ... 1 ... amm +1 ... ... ... amk ... ... ... amn Δj … Y0 Δ1 Δ2 … Δm Δm+1 … Δk … Δn 23 bu yerda Δj= Z j− cj , Y0=∑ i=1 m cibi , Δi= 0,i=1,m , Δk= ∑ i=1 m aijck− ck, k= m+1,n. Jadvaldagi Cbaz bilan belgilangan ustun x1,x2,...,xm bazis o’zgaruvchilarning chiziqli funksiyadagi koeffitsiyentlardan tashkil topgan vektor, ya’ni Cbaz =(c1,c2,… ,cm) (10) Jadvalda har bir Pj vektorning ustiga xj noma’lumning chiziqli funksiyadagi koeffitsiyenti cj yozilgan. m +1 - qatorga esa x1,x2,...,xm bazis o’zgaruvchilardagi chiziqli funksiyaning qiymati Y0= ∑ i=1 m bici (11) hamda bazis yechimning optimallik mezonini baholovchi son Δ j= Z j− cj= ∑ i=1 m aijci− cj (i=1,...,m ; j=1,...,n) (12) yozilgan. Bazis o’zgaruvchilarga mos keluvchi P1,P2,...,Pm vektorlar bazis vektorlar deb belgilangan. Bu vektorlar uchun Δ j= Z j− cj= 0 ( j=1,m ) bo’ladi. Agar barcha ustunlarda Δj≤ 0 bo’lsa, u holda X=(x1,x2,...,xm)=(b1,b2,...,bm) yechim optimal yechim bo’ladi. Bu yechimdagi chiziqli funksiyaning qiymati Y1 ga teng bo’ladi. max Zj−cj>0 (Z j− cj)= Zk− ck= Δk shartni qanoatlantiruvchi Pk vektorni bazisga kiritib, bazisdan min aik>0 (bi¿aik)= bl¿alk (13) shartni qanoatlantiruvchi Pl vektorni chiqarish kerak bo’ladi. Bu holda alk element hal qiluvchi element sifatida belgilandi. Shu element joylashgan l -qatordagi Pl vektor o’rniga u joylashgan ustundagi Pk vektor bazisga kiritiladi. Pl vektorning 24 o’rniga Pk vektorni kiritish uchun simpleks jadval quyidagi formulalar asosida almashtiriladi. { b'i= bi− (bl/alk)⋅aik bl '= bl/alk { a'ij= aij− (alj/alk)⋅aik alj'= alj/alk Simpleks jadval almashgandan so’ng yana qaytadan Δj≤ 0 baholar aniqlanadi. Agar barcha j lar uchun Δj≤ 0 bo’lsa, optimal yechim topilgan bo’ladi. Aks holda topilgan bazis reja boshqa bazis reja bilan almashtiriladi. Bunda quyidagi teoremalarga asoslanib ish ko’riladi: 1-teorema. Agar X=(x1,x2,...,xm) bazis reja uchun Δ j= Z j− cj≤ 0 j=1,n tengsizlik o’rinli bo’lsa, u holda bu reja optimal reja bo’ladi. 2-teorema. Agar X0 bazis rejada tayin bir j uchun shart o’rinli bo’lsa, u holda X0 optimal reja bo’lmaydi va shunday X1 rejani topish mumkin bo’ladiki, uning uchun Y(X1)<Y (X0) tengsizlik o’rinli bo’ladi. Agar tayin bir j uchun Δ j= zj− cj> 0 tengsizlik o’rinli bo’lsa, u holda 2 -teoremaga asosan bu bazis rejani ham yangi bazis rejaga almashtirish kerak bo’ladi. Bu jarayon optimal reja topilguncha yoki masaladagi maqsad funksiyaning quyidan chegaralanmagan ekanligi aniqlanguncha takrorlanadi. Masalaning optimal yechimining mavjud bo’lmaslik sharti quyidagicha: Agar tayin j uchun Δ j= zj− cj> 0 tengsizlik o’rinli bo’lib, bu ustundagi barcha elementlar aij≤ 0 (i= 1,m ) bo’lsa, u holda masalaning maqsad funksiyasi chekli ekstremumga ega bo’lmaydi. Faraz qilaylik, simpleks jadvalda optimallik sharti ( Δj≤ 0 , j=1,n ) bajarilsin. 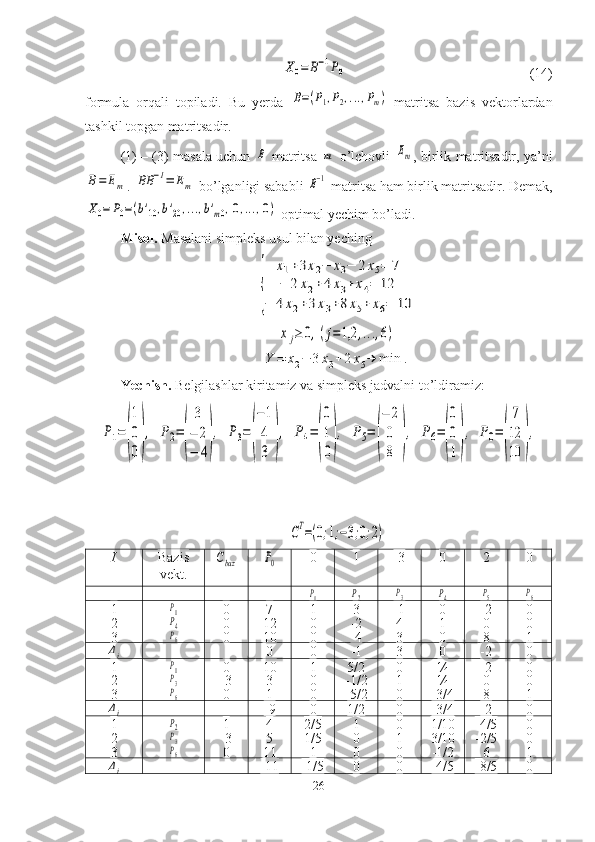Bu holda bu yechim 25 X0= B−1P0(14) formula orqali topiladi. Bu yerda B=(P1,P2,...,Pm) matritsa bazis vektorlardan tashkil topgan matritsadir. (1) – (3) masala uchun B matritsa m o’lchovli Em , birlik matritsadir, ya’ni B= Em . BB −1= Em bo’lganligi sababli B−1 matritsa ham birlik matritsadir. Demak, X0= P0=(b'10,b'20,...,b'm0,0,...,0) optimal yechim bo’ladi. Misol. Masalani simpleks usul bilan yeching { x1+3x2− x3− 2x5= 7 − 2 x2+4x3+x4= 12 − 4x2+3x3+8x5+ x6= 10 xj≥ 0,(j=1,2 ,...,6) Y = x2− 3x3+2x5→ min . Yechish. Belgilashlar kiritamiz va simpleks jadvalni to’ldiramiz: P1= ( 1 0 0) , P2= ( 3 − 2 − 4) , P3= ( − 1 4 3 ) , P4= ( 0 1 0) , P5= ( − 2 0 8 ) , P6= ( 0 0 1) , P0= ( 7 12 10 ) , CT=(0;1;−3;0;2) I Bazis vekt. 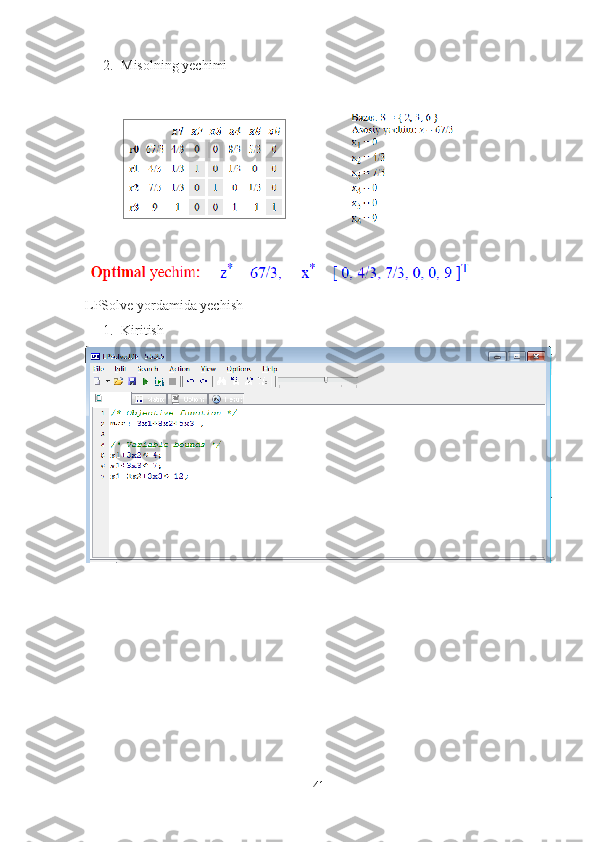Cbaz P0 0 1 -3 0 2 0 P1 P2 P3 P4 P5 P6 1 P1 0 7 1 3 -1 0 -2 0 2 P4 0 12 0 -2 4 1 0 0 3P6 0 10 0 -4 3 0 8 1 Δj 0 0 -1 3 0 -2 0 1 P1 0 10 1 5/2 0 ¼ -2 0 2P3 -3 3 0 -1/2 1 ¼ 0 0 3 P6 0 1 0 -5/2 0 -3/4 8 1 Δj -9 0 1/2 0 -3/4 -2 0 1 P2 1 4 2/5 1 0 1/10 -4/5 0 2P3 -3 5 1/5 0 1 3/10 -2/5 0 3 P6 0 11 1 0 0 -1/2 6 1 Δj -11 -1/5 0 0 -4/5 -8/5 0 26 Simpleks usulning I bosqichida bazisga P3 vektor kiritilib P4 vektor chiqarildi, II bosqichida P2 kiritildi va P1 chiqarildi. Simpleks jadval (7) formulalar asosida almashtirilib borildi. III bosqichda optimal yechim topildi: X=(0;4;5;0;0;11 ),Ymin =−11 . II Bob. Ishlab chiqarishni samarali rejalashtirish va samarali daromad olishni hisoblash uchun dasturiy ta’minot Bu bobda ishlab chiqarishni samarali tashkillashtirish va daromad olishni hisoblash uchun ob’ektga yo‘naltirilgan “PHP” dasturlash tilida yaratilgan viziullashtirilgan dasturiy ta’minotdan foydalanish ishlab chiqarish sohalariga tegishi bo’gan bir nechta hayotiy masalalarning optimal rejasini tuzish va daromad olishni hisoblash orqali ko‘rsatgan. Dasturiy ta’minotni yaratishda [10], [11],[12] adabiyotlardan hamda internet tarmog‘idan foydalanilgan. 2.1. Ishlab chiqarishni samarali rejalshtirish va daromad olish masalalarining matematik modellari Yuqoridagi bobda keltirib o’tganimizdek ishlab chiqarishin rejalashtirish va samarali daromad olish masalalarining matematik modellari asosan chiziqli dasturlash masalasiga keladi. 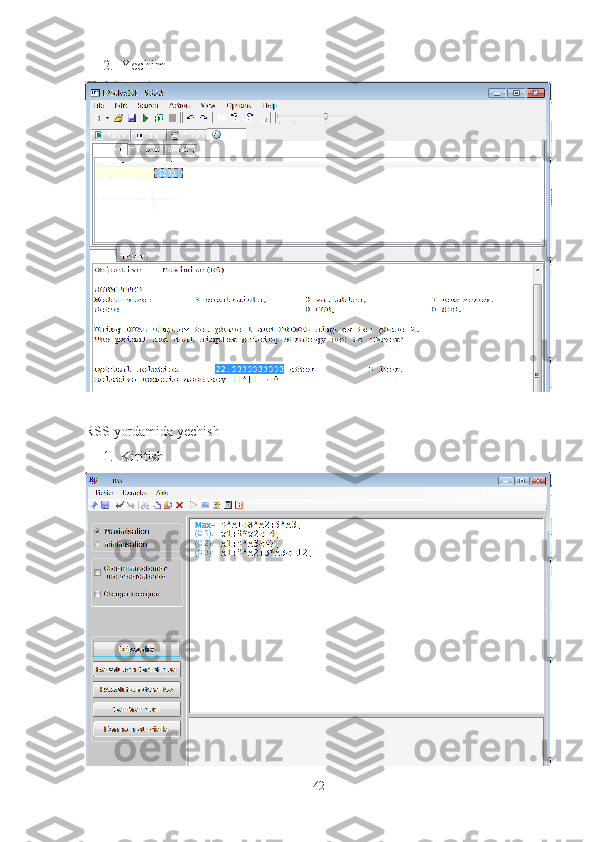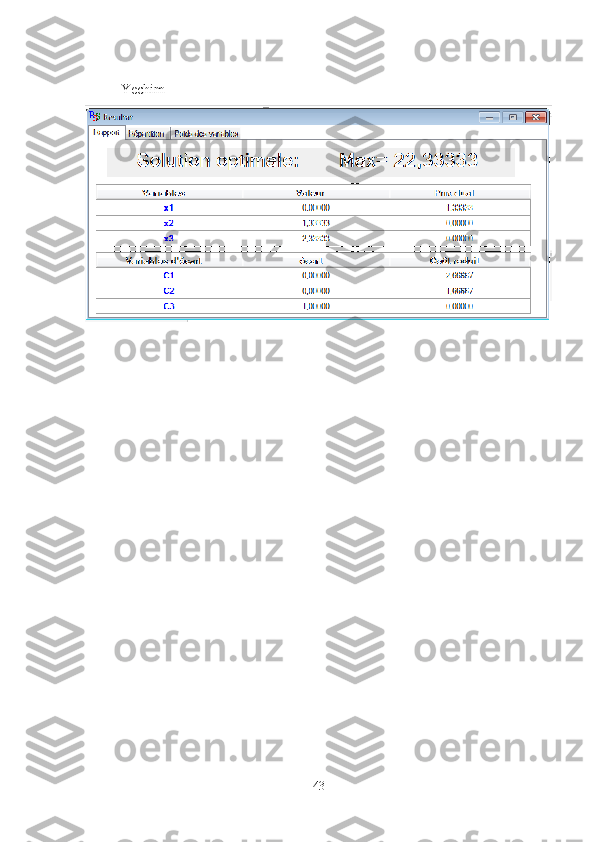Bu masalani yechish uchun bir qancha usullar mavjud, simpleks, ikkilik simpleks, grafik usullari va hakozolar. Bundan tashqari bu masalani yechish uchun bir qancha dasturiy taminotlar ham mavjud, masalan LINDO, LPSolve va hakozolar. Biz quyida ishlab chiqarish sohalariga tegishli bo’lgan bir nechta sodda masalalrning matematik modellarini tuzamiz va bu masalalarni simpleks usuliga asoslangan php dasturlash tili yordamida yaratgan dasturiy taminotimizdan foydalanib yechamiz. 27 Misol . Farmasevtika fabrikasi 2 turdagi (A va B) dori ishlab chiqarishni rejalashtirgan. Bu dorilar bir xil shisha idishchalarda ishlab chiqariladi. Fabrikaning hom ashyosi A dori uchun 20000 ta shisha idishchaga yetadi. B dori uchun 40000 ta ammo barcha idishchalarning soni 45000 ta. 1000 shisha idishcha A doridan ishlab chiqish uchun 3 soat vaq ketadi, B doridan shuncha miqdorda ishlab chiqish uchun 1 soat vaqt ketadi. A va B dorilardan ishlab chiqish uchun fabrikaning ixtiyorida 66 soat mavjud. A dorining har bir shishasidan 8 so’m B dorinikidan esa 7 so’m foyda qoladi. Maksimal foyda olish uchun fabrikaning ishlab chiqish rejasi qanday bo’lishi kerak. Yechish. A doridan 1000 shisha ishlab chiqishni X1 orqali belgilaymiz va huddi shunday X2 orqali B doridan 1000 ta ishlab chiqishni belgilaymiz.A doridan 1000 shisha ishlab chiqarish uchun 3 soat vaqt talab qilingani uchun har 1000 ta dori uchun 3X1 vaqt ketadi huddi shunday har 1000 ta B dori uchun X2 vaqt ketadi. Ikkala dorining har 1000 tasini ishlab chiqish uchun 3X1+X2 vaqt ketadi. Fabrikada dori ishlab chiqish uchun 66 soat vaqt bo’lgani uchun ikkita doridan ishlab chiqish uchun ketgan vaqt 66 dan oshmasligi kerak, ya’ni 3X1+X2<=66. Barcha idishlar soni 45000 ta bo’gani uchun hamma ishlab chiqilgan A va B dorilar soni idishlar sonidan oshmaydi, ya’ni X1+X2<=45. A dorini ishlab chiqish uchun xomashyo 20000 idishga va B dorini ishlab chiqich uchun hom ashyo 40000 idishga yetishini e’tiborga olib ushbu shartlarni olamiz X1<=20 va X2<=40. A dorining har bir shishasi uchun foydaning 8 so’mligina va B dori uchun 7 so’mligini e’tiborga olsan u holda umumiy foyda 8000X1+7000X2 ko’rinishda bo’ladi va yana shisha idishlar soni nomanfiyligini e’tiborga olsak X1>=0 va X2>=0 ga ega bo’lamiz. Shunday qilib berilgan masalaning matematik modeli quydagicha ekan: Max: Y=8000X1+7000X2 3X1+X2<=66 X1+X2<=45 X1<=20 X2<=40 28 X1>=0, X2>=0. Demak masalning matematik modeli 2 ta o’zgaruvchi (X1 va X2) va 4 ta chegaraviy shartlar (cheklanmalar)dan iborat bo’lgan chiziqli dasturlash masalasiga keldi. Misol. Korxona bolalar uchun 2 turdagi (A va B) o’yinchoq ishlab chiqaradi. Har bir B o’yinchoqni ishlab chiqish A o’yinchoqni ishlab chiqishga nisbatan 2 marta ko’p vaqt talab qiladi va korxonaning o’yinchoq ishlab chiqarish uchun kunlik vaqti maksimumi 2000 dona o’yinchoq ishlab chiqarishga etadi. Hom ashyo (plastik) zaxirasi bir kunda 1500 ta o’yinchoq ishlab chiqarishga yetadi. B o’yinchoqni qo’shimcha bezash uchun kunlik 600 tasiga yetadigan hom ashyo bor. Agar korxona A o’yinchoqdan 3 so’m va B o’yinchoqdan 5 so’mdan foyda olsa, bir kunda nechta qo’g’rchoq ishlab chiqish kerak? (maksimal foyda olish uchun) Yechish. Dastlab masalaning masalaning matematik modelini tuzamiz. X1 va X2 bilan , mos ravishda bir kunda ishlab chiqariladigan A va B o’yinchoq lar sonini belgilaymiz. A qo’g’irchoqni ishlab chiqarish uchun t soat vaqt talab qilinsin, u holda B qo’g’irchoqni ishlab chiqarish uchun 2t vaqt kerak bo’ladi. Demak X1 va X2 o’yinchoq larni ishlab chiqarish 2000t soatdan oshmasligi kerak. Shuning uchun tX1+2tX2<=2000t. Xomashyo zaxirasini e’tiborga olib, X1+X2<=1500 shartni olamiz va ikkinchi o’yinchoq uchun qo’shimcha hom ashyo miqdorini e’tiborga olib X2<=600 ni hosil qilamiz. Bundan tashqari o’yinchoqlar soni nomanfiy va umumiy foyda 3X1+5X2 ko’rinishda bo’ladi. Demak masalaning matematik modeli quyidagicha: Max: Y=3X1+5X2 X1+2X2<=2000 X1+X2<=1500 X2<=600 X1>=0, X2>=0. 29 Bu chiziqli dasturlash masalasini keyingi paragrafda yechamiz, buning uchun biz o’zimiz yaratgan dasturiy ta’minotdan foydalanamiz va shu tariqa ushbu dasturiy ta’minotda foydalanish uchun ko’rsatma ham berib o’tamiz. 2.2. Dasturiy ta’minotdan foydalanuvchilar uchun ko’rsatma Dasturiy ta’minotdan foydalanuvchilar uchun ko’rsatmani yuqoridagi paragrafda keltirilgan misollarni yechish orqali keltiramiz. Dasturiy ta’minotning ko’rinishi quyidagicha: 2.1-rasm. Dasturiy ta’minotning asosiy oynasi . Ushbu dasturda masalani yechish uchun dastlab “Yangi masala kiritish” tugmasi bosiladi. Undan keyin ekranda “immissione_dati_0.php” sahifasi ochiladi. Bu sahifada masaladagi noma’lumlar va cheklovlar sonini kiritamiz. ( 2.2- rasm) 2.2-rasm. Dasturiy ta’minotning o’zgaruvchilar va cheklovlar sonini kiritish oynasi . Ma x: Y=8000X1+7000X2 3X1+X2<=66 X1+X2<=45 X1<=20 X2<=40 X1>=0, X2>=0. Masalan, quyidagi chiziqli dasturlash masalasini qaraylik. Ushbu masala uchun 30 noma’lumlar soni 2 ta , cheklovlar soni esa 4 ta. Sonlarni kiritib, “Hisoblash” tugmasini bosganimzda “immissione_dati_1.php” sahifasi ochiladi. Bu sahifa quyidagicha ko’rinishga ega. 2.3-rasm. Dasturiy ta’minotning masala kiritilgan oynasi . Ushbu sahifada masalani dasturga kiritamiz va “Hisoblash” tugmasini bosamiz. Natijada bizga “simplesso.php” sahifasida masalaning yechimi paydo bo’ladi. 31 2.4-rasm. Masalning yechimi keltirilgan oyna . Demak dasturga ko’ra masalaning yechimi quyidagiga teng ekan: X1*=10.5 X1*=34.5 Y*=32550 Misol. Korxona bolalar uchun 2 turdagi (A va B) o’yinchoq ishlab chiqaradi. Har bir B o’yinchoqni ishlab chiqish A o’yinchoqni ishlab chiqishga nisbatan 2 marta ko’p vaqt talab qiladi va korxonaning o’yinchoq ishlab chiqarish uchun kunlik vaqti maksimumi 2000 dona o’yinchoq ishlab chiqarishga etadi. Hom ashyo (plastik) zaxirasi bir kunda 1500 ta o’yinchoq ishlab chiqarishga yetadi. B o’yinchoqni qo’shimcha bezash uchun kunlik 600 tasiga yetadigan hom ashyo bor. Agar korxona A o’yinchoqdan 3 so’m va B o’yinchoqdan 5 so’mdan foyda olsa, bir kunda nechta qo’g’rchoq ishlab chiqish kerak maksimal foyda olish uchun. Yechish. Dastlab masalaning masalaning matematik modelini tuzamiz. X1 va X2 bilan , mos ravishda bir kunda ishlab chiqariladigan A va B o’yinchoq lar sonini belgilaymiz. A qo’g’irchoqni ishlab chiqarish uchun t soat vaqt talab qilinsin, u holda B qo’g’irchoqni ishlab chiqarish uchun 2t vaqt kerak bo’ladi. Demak X1 va X2 o’yinchoq larni ishlab chiqarish 2000t soatdan oshmasligi kerak. 32 Shuning uchun tX1+2tX2<=2000t. Xomashyo zaxirasini etiborga olib X1+X2<=1500 shartni olamiz va ikkinchi o’yinchoq uchun qo’shimcha xomashyo miqdorini e’tiborga olib X2<=600 ni hosil qilamiz. Bundan tashqari o’yinchoqlar soni nomanfiy va umumiy foyda 3X1+5X2 ko’rinishda bo’ladi. Demak, masalaning matematik modeli quyidagicha: Max: Y=3X1+5X2 X1+2X2<=2000 X1+X2<=1500 X2<=600 X1>=0, X2>=0. Bu chiziqli dasturlash masalasini yechish uchun dasturiy taminotdan foydalanamiz. 2.5-rasm. Dasturiy ta’minotning o’zgaruvchilar va cheklovlar sonini kiritish oynasi . 2.6-rasm. Dasturiy ta’minotning masala kiritilgan oynasi . 33 2.6-rasm. Masalaning yechimi keltirilgan oyna Demak dasturga ko’ra yechim quyidagiga teng: X1*=1000 34 X2*=500 Y*=5500 Bu esa A o’yinchoqdan 1000 dona B o’yinchoqdan 500 dona ishlab chiqarishni va o’sha holda optimal daromad olishni bildiradi daromad esa 5500 so’mga teng bo’ladi. 2.3. Dasturiy ta’minotni boshqa mavjud bolgan dasturiy taminotlar bilan taqqoslash. Ushbu paragrafda biz yaratgan dasturiy taminotni boshqa mavjud bo’lgan dasturiy ta’minotlar bilan taqqoslaymiz. Albatta bizning dasturimiz soda bo’lib bir vazifani bajarishga yo’naltirilgan, ya’ni faqat chiziqli dasturlash masalasini simpleks usuli yordamida yechadi. Bizning maqsadimiz yaratgan dasturimizning berilgan masalani qanchalik darajada to’g’ri yechishini tekshirishdan iborat va shuning uchun taqqoslash o’tkazamiz. Taqqoslashni, bir xil masalani bir nechta dasturlar yordamida yechish bilan o’tkazamiz. Internet tarmog’dan LPSolve, LINDO6.1, RSS kabi dasturlarni topdik. Bu dasturlar ko’p funksiyali mukammal dasturlar bo’lib, ular bir qancha chiziqli, chiziqli bo’lmagan, dinamik, qavariq va boshqa dasturlash masalalarini bir nechta usullar bilan yechishga mo’ljallangan. Taqqoslashni eng soda masaladan boshlaymiz, ya’ni yuqorida yechilgan masalalardan birini boshqa dasturlar yordamida yechib ko’ramiz. Yuqoridagi ikkinchi masala, o’yinchoq ishlab chiqarish masalasini qaraylik, bizning dasturimizga ko’ra optimal yechim quyidagicha edi: X1*=1000 X2*=500 Y*=5500 Endi bu masalani LPSolve dasturi yordamida yechamiz. 35 2.7-rasm. LPSolve5.5.2.5 ning masala kiritilgan oynasi . 2.8-rasm. LPSolve5.5.2.5 ning masala yechimini keltirgan oynasi . Ikkinchi oynadan ko’rinib turibdiki masalaning yechimi bizning yechim bilan bir xil chiqqan, ya’ni 36 X1=1000 X2=500 va optimal yechim 5500 Endi ikkinchi dastur LINDO6.1 yordamida huddi shu masalani yechamiz. 37 2.9-rasm. LINDO6.1 ning masala kiritilgan oynasi . 2.10-rasm. LINDO6.1 ning masala yechimini keltirgan oynasi . Bu yerda ham ikkinchi oynada masalaning yechimi keltirilgan va u ham bizning natija bilan bir xil ya’ni maqsad funksiyasining qiymati 5500, o’zgaruvchilarning qiymatlari X va Y lar mos ravishda 1000 va 500 ga teng. Endi masalani uchinchi dastur yordamida yechamiz, dastur fransuz tilida. 38 2.11-rasm. RSS ning masala kiritilgan oynasi . 2.12-rasm. RSS ning masala yechimini keltirgan oynasi . Ushbu dastur ham bir xil natijani berdi. Demak, eng sodda masala uchun natijalar bir xil chiqdi. Endi quyidagi misollarni yechish orqali dasturiy ta’minotni taqqoslaymiz. 39 { x1+2x2+x3= 6, x1+x2+x4= 9, 3x1− x2+x5= 12 ,b ) { x1− x2− 2x3= 4, 2x1+4x3+x4= 8, x3+x5= 6, xj≥ 0 (j= 1,..,5). xj≥0 (j=1,..,5). Y= 7x1+x2− 4x3+x4→ max . Y = x1+2x2− x3− x4− 2x5→ max . d ) {x 1 +3x 2 ≤4,¿{x 1 +3x 3 ≤7,¿¿¿¿ xj≥0 (j=1,..,3). Y = 3x1+8x2+5x3→ max . Dasturiy ta’minotlar yordamida yechish: 1. Misolning kiritilishi 40 2. Misolning yechimi LPSolve yordamida yechish 1. Kiritish 41 2. Yechim RSS yordamida yechish 1. Kiritish 42 Yechim 43 Xulosa Bitiruv malakaviy ishida ishalab chiqarishni samarali rejalashtirish masalalari va ularni yechish uchun olingan matematik modellar bilan tanishib chiqildi hamda bu modellardan biri bo’lgan chiziqli dasturlash masalasini simpleks usuli yordamida yechishga asoslangan dasturiy ta’minot yaratildi. Bu dasturiy ta’minotdan foydalanib, turli xil cheklanmalar orqali berilgan chiziqli dasturlash masalalarini yechish mumkin, bu masalalar ishlab chiqarishni rejalashtirish va samarali daromad olish masalalarining asosiy matematik modellaridan biri hisoblanadi. Chiziqli dasturlash masalasi simpleks usuliga asoslanib yechiladi. Dasturiy ta’minot yordamida olingan chiziqli dasturlash maslasining yechimi ishlab chiqarishni optimal rejalashtirish va optimal daromad olishning yechimi bo’ladi, ya’ni maqsad funksiyasining maksimumi optimal daromad olishga va shu funksiyani maksimumga yerishtiruvchi o’zgaruvchilarning qiymati optimal rejalarga mos keladi. Ishda olingan natijalar va unda qo‘llanilgan usullardan turli iqtisodiy, ijtimoiy sohalarning ko‘pgina amaliy masalalari, jumladan, ishlab chiqarishni samarali rejalashtirish va daromad olishni tadqiq qilishda, ularning dasturiy ta’minotini yaratishda, “Jarayonlar tadqiqoti”, “Chekli o’lchovli ekstemal masalalar”, va shu kabi fanlarning amaliy mashg‘ulotlari o‘quv jarayonlarida dasturiy vosita sifatida foydalanish mumkin. 44 Foydalanilgan adabiyotlar 1. Вагнер Г. Основы исследований операции. Т. 1–3. М.: Мир. 1972-73. 2. Ху Т. Целочисленное программирование и потоки в сетях. М.: Мир, 1974. 3. Зайченко Ю. Б. Исследование операций. Киев. 1979. 4. Таха Х. Введение в исследование операций. Т. 1, 2. М.: Мир. 1981. 5. Q. Safayeva. Matematik dasturlash. Darslik. TMI-2003y. 6. Волков И. К., Загоруйко Е. А. Исследование операций. М.:Изд. МГТУ им. Н. Э. Баумана.- 2000. 7. Конюховский П. В. Математические методы исследования операций. Ст. Петербург. Изд. Питер.- 2001. 8. Вентцель Е. С. Исследование операций. Задачи, принципы, методология. М.: Высшая школа.- 2001. 9. Афанасьев М. Ю., Суворов Б. П. Исследование операций в экономике: модели, задачи, решения. М.: Инфра – М.- 2003. 10. PHP 7 Д. В. Котеров И. В. Симдянов СПб.: БХВ – Петербург, 2016. - 1088 11. . https :// www . w 3 schools . com / php / default . asp 45 ILOVA _____________________________________________________________________________ ____ index.php <?php require 'template.php'; $title = "PHPda SIMPLEKS METODni amalga oshirish"; $content = ''; $pagina = new template; $pagina->setta_titolo($title); $pagina->setta_filename(basename($_SERVER["SCRIPT_NAME"])); $pagina->setta_contenuto($content); print ($pagina->mostra_pagina()); ?> _____________________________________________________________________________ ____ immissione_dati_0.php <?php require 'template.php'; $content = ' <script language="javascript" type="text/javascript"> function checkData () { if (document.form0.numVariables.value == "" || document.form0.numConstraints.value == "") { alert("Devi riempire interamente il modulo prima di procedere.") return false } if (! isFinite(document.form0.numVariables.value) || document.form0.numVariables.value < 0 || document.form0.numVariables.value > 10) { alert("Introduci come numero delle variabili di decisione valori compresi fra 0 e 10 . ") return false } if (! isFinite(document.form0.numVariables.value) || document.form0.numConstraints.value < 0 || document.form0.numConstraints.value > 10) { alert("Introduci come numero di vincoli valori compresi fra 0 e 10. ") return false } document.form0.submit() } </script> <form name="form0" method="post" action="immissione_dati_1.php"> <p>Tanlang <input type="radio" name="minmax" value="min" checked><strong>min</strong> <input type="radio" name="minmax" 46 value="max"><strong>max</strong></p> <p>O\'zgaruvchilar soni <input type="text" name="numVariables" size="3" maxlength="3"></p> <p>Cheklovlar soni: <input type="text" name="numConstraints" size="3" maxlength="3"></p> <p>Manfiy o\'zgaruvchilar mavjud <input type="checkbox" name="intera" value="true"></p> <table border="0" summary="invio form"> <thead> <tr> <th><input type="button" value=" Hisoblash " onClick="checkData()"></th> <th><input type="reset" value=" Bekor qilish "></th> </tr> </thead> </table> </form> '; $title = 'Masalaning turini tanlang'; $pagina = new template; $pagina->setta_titolo($title); $pagina->setta_filename(basename($_SERVER["SCRIPT_NAME"])); $pagina->setta_contenuto($content); print ($pagina->mostra_pagina()); ?> _____________________________________________________________________________ ____ immissione_dati_1.php <?php require 'template.php'; foreach ($_POST as $var => $value) { $$var = $value; } date_default_timezone_set('UTC'); $content = '<script language="javascript" type="text/javascript"> function looksLikeANumber(theString) { // returns true if theString looks like it can be evaluated var result = true; var length = theString.length; if (length == 0) return (true); // valutato da simplesso.php come var x = "" var y = "1234567890-+*. /" var yLength = y.length; for (var i = 0; i <= length; i++) { x = theString.charAt(i); result = false; for (var j = 0; j <= yLength; j++) { 47 if (x == y.charAt(j)) {result = true; break} } // j if (result == false) return(false); } // i return(result); } // looks like a number function checkData(dataForm) { for (var i = 0; i < dataForm.length-2; i++) { name = dataForm.elements[i].name; if (name.substr(0,3) == "lge" || name == "minmax" || name == "name" || name == "intera" || name == "XDEBUG_SESSION_START") {} else { if (! looksLikeANumber (dataForm.elements[i].value)) { alert (name + " non e\' un numero!\n") return false } } } // check data dataForm.submit() } </script> <form name="form1" method="post" action="simplesso.php"> <input type="hidden" name="minmax" value="' . $minmax . '"> <input type="hidden" name="numVariables" value="' . $numVariables . '"> <input type="hidden" name="numConstraints" value="' . $numConstraints . '"> <input type="hidden" name="name" value="tmp' . date("siH") . '">' . '<input type="hidden" name="XDEBUG_SESSION_START" value="testID">' . '<input type="hidden" name="XDEBUG_PROFILE" value="">' . "\n"; if (isset($intera) && !strcmp($intera, "true")) $content.= '<input type="hidden" name="intera" value="true">'; else $content.= '<input type="hidden" name="intera" value="false">'; $content.= ' <strong>' . $minmax . ' z = '; // 1ma riga: c^t x + ... for ($j = 0; $j < $numVariables; $j++) { $content.= sprintf("<input type=\"text\" name=\"c[%d]\" size=\"5\" maxlength=\"5\"> x<sub>%d</sub> +\n", $j + 1, $j + 1); } $content.= ' <input type="text" name="d" size="5" maxlength="5"><br><br><br><br>'; for ($i = 0; $i < $numConstraints; $i++) { $content.= $i + 1 . ') '; $content.= sprintf("<input type=\"text\" name=\"a[%d][1]\" size=\"5\" maxlength=\"5\"> x<sub>1</sub>\n", $i + 1); for ($j = 1; $j < $numVariables; $j++) { $content.= sprintf("+ <input type=\"text\" name=\"a[%d][%d]\" size=\"5\" 48 maxlength=\"5\"> x<sub>%d</sub>\n", $i + 1, $j + 1, $j + 1); } $content.= sprintf("<select name=\"lge[%d]\"><option>=&lt;<option>&gt;=<option>=</select> <input type=\"text\" name=\"b[%d]\" size=\"5\" maxlength=\"5\"><br>\n", $i + 1, $i + 1); } $content.= '&nbsp; &nbsp; x<sub>i</sub> &gt;= 0'; if (isset($intera) && !strcmp($intera, "true")) $content.= ' '; $content.= ' &nbsp; i =1,...,' . $numVariables; $content.= '</strong><br> <table border="0" summary="invio form"> <thead> <tr> <th><input type="button" value=" Hisoblash " onClick="checkData(this.form)"></th> <th><input type="reset" value=" Bekor qilish "></th> </tr> </thead> </table>'; $title = 'Ma\'lumotlarni kiriting'; $pagina = new template; $pagina->setta_titolo($title); $pagina->setta_filename(basename($_SERVER["SCRIPT_NAME"])); $pagina->setta_contenuto($content); print ($pagina->mostra_pagina()); ?> _____________________________________________________________________________ __ template.php <?php class template { var $titolo; var $filename; var $alta; var $bassa; var $pagina; var $contenuto; var $setta_alta; var $setta_bassa; Function setta_titolo($title) { $this->titolo = $title; } Function setta_filename($filename) { $this->filename = $filename; } Function setta_alta() { if (!isset($this->setta_alta)) { $this->setta_alta = 1; } 49 $testata = implode('', file('testata.php')); $keywords = ' <meta name="keywords" content="metodo del simplesso, programmazione lineare, forma standard, forma canonica, tableau, metodo delle due fasi, programmazione lineare intera, medodo dei piani di taglio, variabili slack, variabili surplus, variabili ausiliarie, variabili artificiali, forma di inamissibilità, regione di ammissibilità, Gionata Massi"> '; $style = ' <link rel="StyleSheet" href="stile.css" type="text/css" media="screen">'; $this->alta = '<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN"> <html> <head> <title>Simplex - ' . $this->titolo . '</title> <meta http-equiv="Content-Type" content="text/html; charset=ISO- 8859-1"> <meta name=author content="Gionata Massi"> ' . $keywords . $style . ' </head> <body> <!-- TAGLIA 1 --> <hr align="left" width="100%"> <br> <br> <!-- FINE TESTATA --> '; } Function setta_bassa() { if (!isset($this->setta_bassa)) { $this->setta_bassa = 1; } $this->bassa = ' <!-- INIZIO PIEDE --> <br> <br> <hr align="left" width="100%"> <!-- TAGLIA 2 --> <table border="0" width="100%" cellspacing="0" cellpadding="0" summary="link a fondo pagina"> <thead> <tr> <th width="25%" align="left" valign="top"><a href= "index.php"><img src="images/top.png" alt="[HOME] " height="32" width="32" border="0"> Bosh sahifa</a></th> <th width="25%" align="center" valign="top"><a href= 50 "immissione_dati_0.php"><img src="images/up.png" alt= "[NEW] " height="32" width="32" border="0"> Yangi masala kiritish</a></th> <th width="25%" align="right" valign="top"><a href= "show_src.php?script=' . $this->filename . '" target="sorgenti"> <img src="images/src.png" alt="[SRC] " height="32" width="32" border="0"> Faylning manba kodi</a></th> <th width="25%" align="right" valign="top"><a href= "info.php" target="info"><img src="images/doc.png" alt="[INFO] " height="32" width="32" border="0"> Yo\'riqnoma</a></th> </tr> </thead> </table> <hr width="100%"> <br> <br> </body> </html>'; } Function setta_contenuto($content) { $this->contenuto = $content; } Function mostra_pagina() { header("Cache-Control: no-store, no-cache, must-revalidate"); if (!isset($this->setta_alta)) { $this->setta_alta(); } if (!isset($this->setta_bassa)) { $this->setta_bassa(); } $this->pagina = $this->alta . '<h2>' . "$this->titolo" . '</h2>' . $this->contenuto . $this->bassa; return ($this->pagina); } } ?> 51

ISHLAB CHIQARISHNI REJALASHTIRISH MASALASINI TADQIQ QILISH VA DASTURIY TA’MINOTINI YARATISH 1

MUNDARIJA KIRISH……………………………………………………………… 3 1-BOB Ishlab chiqarish va uni rejalashtirish masalasining umumiy tavsifi ………………. . ……… . ……………………............................. 6 1 .1 Ishlab chiqarishni rejalashtirish va undagi samaradorlik tushunchalari 6 1.2 Ishlab chiqarishni tashkil qilish va rejalashtirish masalalari …...... …... 7 1.3 Chiziqli dasturlash masalasining umumiy qo‘yilishi ............................. 1 1 1.4 Chiziqli dasturlash masalasini yechish uchun simpleks usul …. ……... 2 2 2-BOB Ishlab chiqarishni rejalashtirish va samarali daromad olish masalalari uchun dasturiy ta’minot ………………………………. 27 2 .1 Ishlab chiqarishni samarali rejalashtirish va daromad olish masalalarining matematik modellari ………………………………. 27 2.2 Dasturiy ta’minotdan foydalanuvchilar uchun ko‘rsatmalar ............... 29 2.3 Dasturiy taminotni boshqa mavjud bo‘lgan dasturiy ta‘minotlar bilan taqqoslash ………………………………………………………….. 35 XULOSA…………………………………………………………….. 44 Foydalanilgan adabiyotlar.………………………………………… 45 ILOVALAR 2

Kirish Masalaning qo‘yilishi. Ishlab chiqarishni tashkil etishda samarali reja va daromad olish masalalarini tadqiq qilish va matematik modellari chiziqli dasturlash masalasiga keluvchi ishlab chiqarish masalalari uchun qulay interfeysga ega bo‘lgan dasturiy ta‘minot yaratish. Mavzuning dolzarbligi. Jamiyatning barcha sohalarida ishlab chiqarish va daromad olishni optimallashtirish muhum masala hisoblanadi. Ayniqsa bugungi kunda rivojlanayorgan, shiddat bilan sanoatlashayotgan jamiyatda, tabiiy holda raqobatning kuchayishi ortidan ishlab chiqarishni optimal rejalashtirish va optimal daromad olish eng dolzarb masalalardan biri bo’lib qolmoqda. Ishlab chiqarishni optimallashtirish masalalari nazariy jihatdan, ya’ni ularning matematik va boshqa modellarini yaratish ularni yechish va hakozolar, birmuncha yaxshiroq o’rganilgan bo’lishiga qaramay amaliy jihatda o’rganishga yetarlicha ishlar mavjud bo’lib bulardan biri bu nazariy tomondan yaratilgan modellar uchun dasturiy ta’minot yaratish. Shuning uchun bu ishda ishlab chiqarishni samarali rejalashtirish va daromad olish masalalari uchun dasturiy taminot yaratish masalasi qaraladi. Ishning maqsad va vazifalari. Bitiruv malakaviy ishning asosiy maqsad va vazifasi bu ishlab chiqarish sohalar, ularning turi, yo’nalishi, ishlab chiqarish jarayoni, moddiy ta’minoti va boshqa parametrlariga ko’ra optimal rejalari va daromadlarini hisoblashlarni yengillashtirish. Ilmiy-tatqiqot usullari. Ushbu bitiruv malakaviy ishida ishlab chiqarishni tashkil etishda eng samarali reja va doromad olish masalalarining matematik modeli chiziqli dasturlash masalasiga keladigan hollar uchun o’rganilgan bo’lib bu modelni yechish uchun yaratilgan dasturiy ta’minot simpleks usuliga asoslangan. Mavzuning o‘rganilish darajasi. Yuqorida aytib o’tganimizdek ishlab chiqarishni va daromadni optimallashtirish masalasi nazariy jihatdan ko’plab olimlar tomonida yaxshi o’rganilgan bo’lib ular ushbu masalaning turli xil modellarini yaratish va ularni yechish kabi natijalarni olishgan. Bu kabi natijalar 3

keltirilgan ko’plab adabiyotlar mavzuni tadqiq qilishda o’rganilgan. Mavzuning o’rganilishi boshlang’ch darajada bo’lib, bu mavzuni o’rganish natijasida olingan natija ya’ni yaratilga dasturiy ta’minot sodda bo’lib u faqat bir yo’nalishga mo’ljallangan hisob kitoblarni bajaradi. Bu dasturiy ta’minotni kelajakda yanada mukammallashtirish rejalashtirilgan. Tadqiqotning ilmiy yangiligi. Bitiruv malakaviy ishida olingan natijalar amaliy-uslubiy xarakterga ega bo‘lib, ishda ishlab chiqarishni eng samarali rejalashtirish va daromad olish masalalarini yechishga mo’ljallangan dasturiy ta’minot yaratligan. Bu dasturiy ta’minot PHP dasturlash tilida yaratilgan bo’lib, u vizuallashgan qulay interfeysga ega. Tadqiqot predmeti va ob’ekti. Tadqiqotning predmeti “Jarayonlar tadqiqoti”, “Iqtisodiyotda jarayonlar tadqiqoti”, “Iqtisodiyot masalalarini matematik modellashtirish”, “Matematik dasturlash” , “Java dasturlash tili” va shu kabi fan sohalari bo‘lib, ob’ekti ishlab chiqarishni rejalshtirish masalalarining matematik modellaridan iborat. Tatqiqotnig ilmiy va amaliy ahamiyati. Ishda olingan natijalar va unda qo‘llanilgan usullardan turli iqtisodiy, ijtimoiy sohalarning ko‘pgina amaliy masalalari, jumladan, ishlab chiqarishni rejalashtirish va samarali daromad olish masalalarini tadqiq qilishda, “Jarayonlar tadqiqoti”, “Iqtisoriyotda jarayonlar tadqiqoti”, “Iqtisodiyot masalalarini matematik modellashtirish” va shu kabi fanlarning amaliy mashg‘ulotlari o‘quv jarayonlarida dasturiy vosita sifatida foydalanish mumkin. Ishning tuzilishi. Ushbu ish kirish, ikki bob, xulosa, foydalanilgan adabiyotlar ro‘yxati va ilovalardan iborat. I bob to‘rtta paragrafdan iborat bo‘lib, unda adabyotlardan foydalanilgan holda, bitiruv malakaviy ishiga qo’yilgan “ Ishlab chiqarishni tashkil etishda samarali reja va daromad olish” masalasi ni tavfislash va natija olish uchun zarur bo‘lgan asosiy tushunchalar, ta’riflar, tasdiqlar va matematik modellar keltirilgan. Bularning asosiylari quyidagilardan iborat: Ishlab chiqarishni tashkil qilish va 4

rejalashtirish masalalari va ularning qo’yilishi, Chiziqli dasturlash masalalari va ularning shakllari, Chiziqli dasturlash masalalarini yechish usullari-Simpleks usuli. II bob uchta paragrafdan iborat bo’lib, birinchi paragrafda ishalab chiqarishni tashkil etishda samarali reja va daromad olish masalalarining matematik modellari haqida so’z yuritilgan, ikkinchi paragrafda bu modellardan biri bo‘lgan chiziqli dasturlash masalasini simpleks usuli orqali yechishga asoslangan PHP dasturlash tilida qulay interfeysga ega bo‘lgan dasturiy ta’minotning funksional sxemasi keltirilgan hamda turli masalalarni yechish orqali dasturiy ta’minotdan foydalanuvchilar uchun ko‘rsatmalar berilgan . Uchinchi paragrafda dasturiy ta’minotning to’gri ishlashini tekshirish uchun bir nechta mavjud standartlashgan dasturiy ta’minotlar bilan taqqoslashlar o’tkazilgan. Olingan natijalarning qisqacha mazmuni. Bitiruv malakaviy ishida ishalab chiqarishni samarali rejalashtirish masalalari va ularni yechish uchun olingan matematik modellar bilan tanishib chiqildi hamda bu modellardan biri bo’lgan chiziqli dasturlash masalasini simpleks usuli yordamida yechishga asoslangan dasturiy ta’minot yaratildi. Bu dasturiy ta’minotdan foydalanib, turli xil cheklanmalar orgali berilgan chiziqli dasturlash masalalarini yechish mumkin, qaysiki bu masalalar ishlab chiqarishni rejalashtirish va samarali daromad olish masalalarining asosiy matematik modellaridan biri hisoblanadi. Chiziqli dasturlash masalasi simpleks usuliga asoslanib yechiladi. Dasturiy ta’minot yordamida olingan chiziqli dasturlash masalasining yechimi ishlab chiqarishni optimal rejalashtirish va optimal daromad olishning yechimi bo’ladi, ya’ni maqsad funksiyasining maksimumi optimal daromad olishga va shu funksiyani maksimumga erishtiruvchi o’zgaruvchilarning qiymati optimal rejalarga mos keladi. 5

Похожие

ISHLAB CHIQARISHNI REJALASHTIRISH MASALASINI TADQIQ QILISH VA DASTURIY TA’MINOTINI YARATISH
Yarimo'tkazgichlarning tarixini tadqiq qilish.
PROFESSOR-O'QITUVCHILAR ILMIY REYTINGINI SHAKLLANTIRISH VA MONITORING QILISHNING INTELLEKTUAL TIZIM ALGORITMI VA DASTURIY TA’MINOTINI YARATISH
END-TO-END MODELLAR ASOSIDA O‘ZBEK TILIDAGI NUTQNI AVTOMATIK TANIB OLISHNING ALGORITMLARI VA DASTURIY TA’MINOTINI ISHLAB CHIQISH
Bir jinslimas g’ovak muhitlarda anomal modda ko’chishi masalasini sonli tadqiq etish