NORAVSHAN TO’PLAMLAR XUSUSIYATLARI

![Noravshan to’plam tushunchasi - matematik modellarni qurish uchun
noravshan ma’lumotni matematik jihatdan bayon etishga harakat qilingan
urinishlardir. Ushbu tushunchaning zaminida berilgan to’plamni tashkil
qilgan bir xil xususiyatli elementlar shu xususiyatga har xil darajada ega
bo’lishi, demak berilgan to’plamga har xil darajada tegishli bo’lishi
mumkinligi to’g’risidagi tasavvur yotadi. Bunday yondashuvga asosan
“qandaydir element berilgan to’plamga tegishli” ko’rinishidagi mulohazalar
ma’noga ega bo’lmay qoladi, chunki aniq bir element berilgan to’plamni
qanday darajada yoki “qanchalik kuchli” qoniqtirishini ko’rsatish zarur.
U tashuvchi- bu baholanayotgan kvazistatistika doirasidagi kuzatishlarning
barcha natijalari tegishli bo’lgan universal to’plamdir. Masalan, agar biz
paxtaning hosildorligini kuzatayotgan bo’lsak, u holda tashuvchi - o’lchov
birligi senter bo’lgan bir gektardan olinadigan paxta miqdori qo’yilgan
haqiqiy o’qdan ajratilgan kesmadir.
U universal top’lamdagi ~
A noravshan to’plam (fuzzy set) deb ( μ~A,u )
juftliklar majmuiga aytiladi, bunda
μ~A - elementning ~A noravshan
to’plamga tegishlilik darajasidir. Tegishlilik darajasi - [0, 1] oraliqdagi
sondir. Tegishlilik darajasi qanchalik yuqori bo’lsa, universal to’plamning
elementi [116,126,152] noravshan to’plamning xossalariga shunchalik
ko’proq darajada tegishli bo’ladi.
А noravshan to’plam – tashuvchining har bir qiymatiga ushbu qiymatning
A to’plamga tegishlilik darajasi mos qo’yilgan tashuvchining qiymatlar
to’plamidir [107,128]. Masalan: lotin alifbodagi X,Y,Z harflar, albatta,
Alphabet = { A, B, C, X, Y, Z } to’plamga tegishli va shu nuqtai nazardan
Alphabet – ravshan . Lekin “Paxtaning muqobil hosildorligi” to’plamini
tahlil qiladigan bo’lsak, u holda 50 s/ga hosildorlik berilgan noravshan](/data/documents/21a448db-2161-40c9-b723-b5197f33e8fc/page_2.png)
![to’plamga ma’lum darajada tegishli bo’lib, uni tegishlilik funksiyasi deb
ataydilar.
Tegishlilik funksiyasi (membership function) - bu universal to’plamdagi
ixtiyoriy elementning noravshan to’plamga tegishlilik darajasini hisoblashga
imkon beruvchi funksiyadir.
Agar universal to’plam U ={u1,u2,...,uk} chekli sondagi elementlardan
iborat bo’lsa, u holda
~
A noravshan to’plam
~A= ∑
j=1
k
μ~A(uj)/uj ko’rinishida
yoziladi. Uzluksiz U to’plam holida
~A= ∫
[u,u]
μ~A(u)/u belgilashdan
foydalanishga kelishilgan.
Masalan, “paxtaning o’rtacha hosildorligi” tushunchasini noravshan
to’plam ko’rinishida quyidagicha tasvirlash mumkin:
~
A
= 0/21+0.1/22 + 0.3/23 + 0.8/24 +1/25 +1/26 + 0.5/27 +0/28.
1-rasmda “Paxtaning hosildorligi” noravshan to’plamining bir qator
mutaxassislar o’rtasida so’rov o’tkazish orqali hosil qilingan tegishlilik
funksiyasi keltirilgan.](/data/documents/21a448db-2161-40c9-b723-b5197f33e8fc/page_3.png)




![Основной Основной Основной
Основной
Основной
Основной
x
m(x)7-rasm. Noravshan to’plam
α
- darajali noravshan to’plam.
Tegishlilik qiymatlari ma’lum
α∈[0,1 ] darajadan yuqori bo’lgan
elementlarning oddiy to’plami A to’plamning
α -kesimi Аα deyiladi:
Аα= {x∈ X ,μA(x)≥ α}
.
Qat’iy
α -kesim
Аα= {x∈ X ,μA(x)>α}
tariqasida aniqlanadi.
Noravshan to’plam berilgan bo’lsin.
A=0.2/5+0.4/6+0.6/7+0.8/8+0.9/9+1.0/10+0.9/11+0.8/12+
+0.6/13+0.4/14+0.2/15 .
Agar
α=0.3 , α=0.5 va α=0.8 bo’lsa, u holda α -darajali
to’plamlarning ko’rinishi quyidagicha bo’ladi:
A
0,3 =0.4/6+0.6/7+0.8/8+0.9/9+1.0/10+0.9/11+0.8/12+0.6/13+0.4/14,
A
0,5 =0.6/7+0.8/8+0.9/9+1.0/10+0.9/11+0.8/12+0.6/13,
A
0,8 =0.9/9+1.0/10+0.9/11.](/data/documents/21a448db-2161-40c9-b723-b5197f33e8fc/page_9.png)

![A noravshan to’plam B noravshan to’plamga tegishli (А⊆В) deyiladi,
faqat va faqat
∀ x∈X , μA(x)≤ μB(x) bo’lsa. Tengsizlik qat’iy bo’lsa,
tegishlilik qat’iy hisoblanib,
A⊂B orqali belgilanadi.
x
α darajali A ga tegishli bo’ladi, faqat va faqat x∈A bo’lsa, ∀x∈X,μ¯A(x)=1−μA(x) B ga
sust tegishli bo’ladi (
A− ¿αB ), agar X ning barcha elementlari α darajada ¯A
yoki B ga tegishli bo’lsa, matematik ko’rinishda esa
A− ¿αB , agar x∈(¯A∪ B)α
∀ x∈X
yoki
∀ x∈X , max (1− μA(x),μB(x))≥α
.
A>− − ¿B
sust tenglama quyidagicha aniqlanadi:
μA(x)
va μB(x) tegishlilik belgilari ½ dan yoki katta yoki teng, yoki ikkalasi
½ dan kichik yoki teng.
A>− − ¿B , faqat va faqat
∀ x∈X ,min [max (1− μA(x),μB(x)),min (1− μA(x),1−μB(x))]≥1/2
bo’lsa.
Kartezian ko’paytma . Agar
A1,...,An mos ravishda U1,...,Un dagi
norvashan to’plamlar bo’lsa,
A1,...,An kartezian ko’pyatma U1×U2×...×Un
fazodagi
μ A1×...× An(u 1,u 2,...,u n)= min ¿ ¿ ¿
yoki
μA1×...×An(u1,u2,...,un)= μA1(u1)⋅μA2(u2)⋅...⋅μAn(un)
tegishlilik funksiyali noravshan to’plam bo’ladi.
Noravshan qismga agratish.](/data/documents/21a448db-2161-40c9-b723-b5197f33e8fc/page_11.png)

MAVZU : NORAVSHAN TO’PLAMLAR XUSUSIYATLARI REJA: 1. Noravshan to’plamlar balandligi. 2. Normal noravshan to’plam, normallashtirish 3. Noravshan to’plam ifodalovchisi 4. Noravshan bo’sh to’plam, qavariq noravshan to’plam
Noravshan to’plam tushunchasi - matematik modellarni qurish uchun noravshan ma’lumotni matematik jihatdan bayon etishga harakat qilingan urinishlardir. Ushbu tushunchaning zaminida berilgan to’plamni tashkil qilgan bir xil xususiyatli elementlar shu xususiyatga har xil darajada ega bo’lishi, demak berilgan to’plamga har xil darajada tegishli bo’lishi mumkinligi to’g’risidagi tasavvur yotadi. Bunday yondashuvga asosan “qandaydir element berilgan to’plamga tegishli” ko’rinishidagi mulohazalar ma’noga ega bo’lmay qoladi, chunki aniq bir element berilgan to’plamni qanday darajada yoki “qanchalik kuchli” qoniqtirishini ko’rsatish zarur. U tashuvchi- bu baholanayotgan kvazistatistika doirasidagi kuzatishlarning barcha natijalari tegishli bo’lgan universal to’plamdir. Masalan, agar biz paxtaning hosildorligini kuzatayotgan bo’lsak, u holda tashuvchi - o’lchov birligi senter bo’lgan bir gektardan olinadigan paxta miqdori qo’yilgan haqiqiy o’qdan ajratilgan kesmadir. U universal top’lamdagi ~ A noravshan to’plam (fuzzy set) deb ( μ~A,u ) juftliklar majmuiga aytiladi, bunda μ~A - elementning ~A noravshan to’plamga tegishlilik darajasidir. Tegishlilik darajasi - [0, 1] oraliqdagi sondir. Tegishlilik darajasi qanchalik yuqori bo’lsa, universal to’plamning elementi [116,126,152] noravshan to’plamning xossalariga shunchalik ko’proq darajada tegishli bo’ladi. А noravshan to’plam – tashuvchining har bir qiymatiga ushbu qiymatning A to’plamga tegishlilik darajasi mos qo’yilgan tashuvchining qiymatlar to’plamidir [107,128]. Masalan: lotin alifbodagi X,Y,Z harflar, albatta, Alphabet = { A, B, C, X, Y, Z } to’plamga tegishli va shu nuqtai nazardan Alphabet – ravshan . Lekin “Paxtaning muqobil hosildorligi” to’plamini tahlil qiladigan bo’lsak, u holda 50 s/ga hosildorlik berilgan noravshan
to’plamga ma’lum darajada tegishli bo’lib, uni tegishlilik funksiyasi deb ataydilar. Tegishlilik funksiyasi (membership function) - bu universal to’plamdagi ixtiyoriy elementning noravshan to’plamga tegishlilik darajasini hisoblashga imkon beruvchi funksiyadir. Agar universal to’plam U ={u1,u2,...,uk} chekli sondagi elementlardan iborat bo’lsa, u holda ~ A noravshan to’plam ~A= ∑ j=1 k μ~A(uj)/uj ko’rinishida yoziladi. Uzluksiz U to’plam holida ~A= ∫ [u,u] μ~A(u)/u belgilashdan foydalanishga kelishilgan. Masalan, “paxtaning o’rtacha hosildorligi” tushunchasini noravshan to’plam ko’rinishida quyidagicha tasvirlash mumkin: ~ A = 0/21+0.1/22 + 0.3/23 + 0.8/24 +1/25 +1/26 + 0.5/27 +0/28. 1-rasmda “Paxtaning hosildorligi” noravshan to’plamining bir qator mutaxassislar o’rtasida so’rov o’tkazish orqali hosil qilingan tegishlilik funksiyasi keltirilgan.
Ос новной Ос новной Ос нов ной Ос нов ной Ос нов ной Ос нов ной Ос нов ной Ос нов ной Ос нов ной m( u) u1-rasm. Tegishlilik funksiyasining ko’rinishi 20 dan 35 gacha bo’lgan hosildorlik mutaxassislar tomonidan so’zsiz muqobil, 60 va undan yuqoriroq - so’zsiz nomuqobil deb baholandi. 35 dan 60 gacha bo’lgan oraliqda mutaxassislar o’zlarining sinflashtirishlarida noqatiy xulosalarni ko’rsatdilar va bu noqatiylikning tuzilishi tegishlilik funksiyasining grafigida namoyon bo’ldi. Tegishlilik funksiyasini (F-funksiyalarni) qurish masalasi noravshan to’plamlar nazariyasidagi asosiy masalalardan biri bo’lib, bu muammo nafaqat noravshan to’plamlar uchungina muhim hisoblanadi. Tegishlilik funksiyasining aniq ko’rinishi mavjud noaniqlikning haqiqiy holatlarini hisobga olgan holda ushbu funksiyalarning xossalariga oid qo’shimcha farazlar (birinchi tartibli hosilaning simmetrilik, monotonlik, uzluksizlik xossalari) asosida aniqlanadi. Ko’pgina amaliy holatlarda tegishlilik funksiyasi unga oid qismiy axborotdan, aytaylik uning chekli х 1 ,..., х n tayanch nuqtalar to’plamida qabul qilinadigan qiymatlardan kelib chiqqan holda baholanishi kerak.
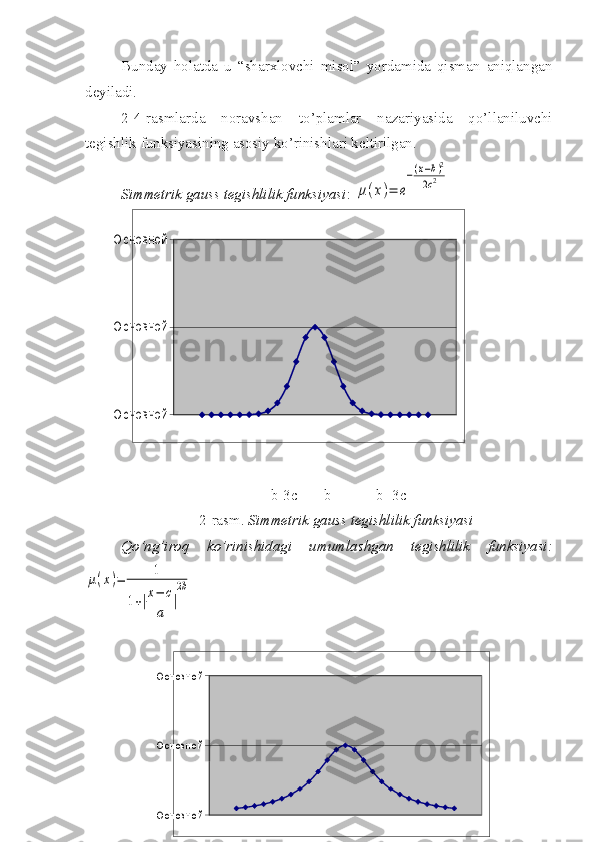
Bunday holatda u “sharxlovchi misol” yordamida qisman aniqlangan deyiladi. 2-4-rasmlarda noravshan to’plamlar nazariyasida qo’llaniluvchi tegishlik funksiyasining asosiy ko’rinishlari keltirilgan. Simmetrik gauss tegishlilik funksiyasi : μ(x)= e −(x−b)2 2c2 b-3c b b+3c 2-rasm. Simmetrik gauss tegishlilik funksiyasi Qo’ng’iroq ko’rinishidagi umumlashgan tegishlilik funksiyasi: μ(x)= 1 1+|x− c a | 2b Основной Основной Основной Основной Основной Основной
