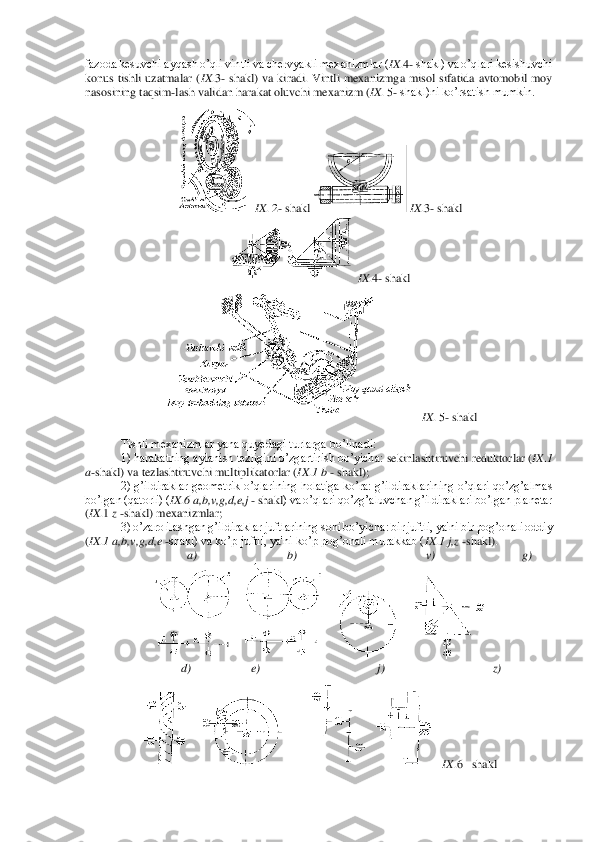
6-mavzu. TISHLI UZATMALAR Reja: 1. Tishli mexanizmlar. Turlari, ishlatilish sohalari. 2. Tishli ilashmaning asosiy qonuni. 3. Evolventali tishli ilashma: elementlari, xossalari va asosiy o’lchamlari. 4. Evolventali tishli ilashma chiqarish va uning sifat kursatkichlari . Adabiyotlar: 1. Yuldoshbekov S.A. Mexanizm va mashinalar nazariyasi. – T.:2006. 2. Djurayev A. va boshq. Mex anizm va mashinalar nazariyasi. -T.: O’qituvchi, 2004. 3. Usmonxo’jayev X..X Mashina va mexanizmlar nazariyasi.Toshkent: O’qituvchi, 1981. 4. Frolov K.V. Mashina va mexanizmlar nazariyasi. – T.: O’qituvchi, 1990. Tayanch iboralar: Tishli mexanizm, tishli reyka , tishli g’ildirak , reduktor , qiya tishli silindrsimon g’ildiraklar , chervyakli uzatma , gipoid uzatma , konussimon g’ildirak , planetar tishli mexanizmlar , Tishli mexanizmlar. Turlari, ishlatilish sohalari. Talab qilinuvchi harakatlarni tarkibida faqat qo’yi kinematik juftliklar bo’lgan mexanizmlar orqali amalga oshirish ularning kinematik sxemasi murakkabligi tufayli hamma vaqt ham maqsadga muvofiq bo’lavermaydi. Bunday hollarda talab qilinuvchi harakatni kam sonli bo’g’inla r yordamida bajariluvchi oliy kinematik juftli mexanizmlar qo’llaniladi. Bunda bo’g’inlarning soni kamida uchta bo’ladi: kirish (yetaklovchi), chiqish (yetaklanuvchi) va qo’zg’almas bo’g’in (tayanch). Muayyan shakldagi egri chiziqli profilga ega bo’lgan ti shlar ko’rinishidagi geometrik elementlarining o’zaro ilashishi orqali bog’langan bo’g’inlardan tuzilgan kinematik zanjirlar tishli mexanizmlar deyiladi. Tishlar bo’g’inning doiraviy sirtida joylashsa - tishli g’ildirak, tekis sirtida joylashsa - tishli re yka hosil bo’ladi. Tishli mexanizmlar odatda aylanma harakatning tezligini va yo’nalishini o’zgartirib uzatish uchun xizmat qiladi, shuning uchun ularni tishli uzatmalar deb ham ataladi. Tishli mexanizmlar yetakchi va yetaklanuvchi bo’g’inlarning aylanish tezliklari doimiy bo’lishi talab qilinadigan hollarda ishlatiladi va texnikada juda ko'p qo’llaniladi. Bu mexanizmning asosiy ko’rinishi IX.l -a shaklda berilgan, u ikkita tishli g’ildirak va stoykalardan iborat. Bo’g’in 2 (yetakchi)ning soat mili yo’nalish iga teskari aylanishi yetaklanuvchi bo’g’in 1 ni soat mili aylanishida aylantiradi. Demak, bu xildagi tishli ilashishda yetakchi va yetak -lanuvchi g’ildiraklar qarama -qarshi tomonga aylanadi. Bunday mexanizm sirtqi ilashishli mexanizm deyiladi. Agar bitta g’ildirakning tishlari silindr tashqi sirtida, ikkin -chiniki ichki sirtida ilashib harakatlansa ( IX. 1 -б shakl), yetakchi va yetaklanuvchi g’ildiraklar bir tomonga aylanadi va bunday mexanizmlar ichki ilashishli mexanizm deyiladi. IX. 1 -shakl Agar tishli g’ildiraklardan birining o’lchamlari juda katta bo'1 -gani holda g’ildirak aylanasi to’g’ri chiziqqa yaqin bo’lsa, bunday birikma reykali mexanizm deyiladi (IX .1-d shakl). Tishli mexanizmlarda aniq aylanish nihoyatda zarur, buni mash ina tirsakli vali bilan gaz taqsimlash valining bir -biriga nisbatan aylanishi misolida ko’rish mumkin ( IX . 2 - shakl). Yuqorida biz tekislikda harakat qiladigan tishli mexanizmlarnigina ko’rdik, bulardan tashqari, texnikada fazoviy shesternyali mexanizmlar ham ko’p ishlatiladi. Bular jumlasiga o’qlari

fazoda kesuvchi ayqash o’qli vintli va chervyakli mexanizmlar ( IX .4- shakl) va o’qlari kesishuvchi konus tishli uzatmalar ( IX .3- shakl) va kiradi. Vintli mexanizmga misol sifatida avtomobil moy nasosining taqsi m-lash validan harakat oluvchi mexanizm ( IX . 5 - shakl)ni ko’rsatish mumkin. IX . 2 - shakl IX .3- shakl IX .4- shakl IX . 5 - shakl Tishli mexanizmlar yana quyedagi turlarga bo’linadi: 1) harakatning aylanish tezligini o’zgartirish bo’yicha: sekinlashtiruvchi reduktorlar ( IX .1 a-shakl) va tezlashtiruvchi multiplikatorlar ( IX .1 b - shakl); 2) g’ildiraklar geometrik o’qlarining holatiga ko’ra: g’ildiraklarining o’qlari qo’zg’almas bo’lgan (qatorli) ( IX .6 a,b,v,g,d,e,j - shakl ) va o’qlari qo’zg’aluvchan g’ildiraklari bo’lgan planetar (IX .1 z -shakl) mexanizmlar; 3) o’zaro ilashgan g’ildiraklar juftlarining soni bo’yicha: bir juftli, ya'ni bir pog’onali oddiy (IX .1 a,b,v,g,d,e -shakl) va ko’p juftli, ya'ni ko’p pog’onali murakkab ( IX .1 j,z -shakl). a) b) v) g) d) e) j) z) IX .6 –shakl

Uzliksiz aylanma harakatni bir valdan boshqasiga berilgan uzatish nisbati bilan uzatish ham ko’pincha tishli uzatmalar yordamida amalga oshiriladi. Tishli mexanizmlar yuqori darajada ishonchli ishlashi hamda berilgan harakat qonunini aniq bajarishi tufayli mashinasozlik va asbobsozlikda juda keng qo’llaniladi. Bulardan tashqari mush tli, friksion, malta va xrapovikli mexanizmlar ham ko’p qo’llaniladi. Tishli uzatmalarda tashqi ( IX .6 - shakl, a), ichki ( IX .6 - shakl - shakl, b) va reykali (IX .6 - shakl, v) ilashmalar farq qilinadi: 1- shesternya, 2- g’ildirak (yoki g’ildirakning xususiy holi - reyka). G’ildiraklar o’qlarining joylashuviga ko’ra tishli mexanizmlar o’qlari parallel joylashgan - silindrsimon ( IX .6 - shakl, a, b), o’qlari kesishuvchi - konussimon ( IX .6 -shakl, g), o’qlari ayqash yoki giperboloid uzatmala r bo’lishi mumkin. Giperboloid uzatmalarning variantlariga vintli ( IX .6 -shakl, d), chervyakli ( IX .6 -shakl, e), gipoid ( IX .6 -shakl, j) uzatmalar kiradi. Vintli uzatmada bo’g’inlar 1, 2 - qiya tishli silindrsimon g’ildiraklar; chervyakli uzatmada bo’g’in 1- chervyak, 2 - chervyak g’ildiragi; gipoid uzatmada bo’g’inlar 1, 2 - konussimon g’ildiraklar. a) b) e) g) d) e) j) IX .6 – shakl Ko’p bo’g’inli tishli uzatmalar - reduktorlar ( IX .7 - shakl, a), planetar tishli mexanizmlar (IX .7 - shakl, b) keng qo’llaniladi. Planetar reduktor tarkibiga o’qlari qo’zg’almas bo’lgan g’ildiraklar 1 va 4 gina emas, balki o’qlari aylana bo’yicha harakatlanadigan g’ildiraklar 2, 3 ham kiradi. IX .7 – shakl Tishli ilashmaning asosiy teoremasi (qonu ni). Tishli mexanizmlarda g’ildiraklarning o’zaro ilashuvchi tishlarining bir -biriga urinuvchi sirtlari, ya'ni profillari aniq belgilangan qonuniyatga asosan loyihalangan bo’lishi kerak. Bu qonuniyat g’ildiraklarning bir -biriga nisbatan aylanma harakatiga qo’yiladigan talablardan kelib chiqadi. Ilashuvchi tishlarining profili va ularning nisbiy harakati orasida bog’lanishni aniqlaylik ( IX .8 -shakl). Shakldan ko’rinib turibdiki, VN1 > V N2 bo’lsa P, profil P2 profilining ichiga botib ketishi, VNi < V N2 bo’lganda esa Pt profil P2 dan orqada qolishi va ular bir -biridan ajralib ketishi mumkin. Bunday hollarning ikkalasiga ham yo'l qo’yib bo’lmaydi, demak P, va P2 profillarning nisbiy harakatida uzluksiz urinishlar iga erishish uchun birinchi navbatda VN1 = V N2 tenglikni ta'minlovchi

ω1(O 1M1) = - ω2O2M2) sharti bajarilishi kerak. Ilashuvchi sirtlar geometriyasini belgilovchi ikkinchi shart Vt va V2 tezliklarning urinma chiziq KK ga proektsiyalarining munosabatidan kelib chiqadi. Agar proektsiyalar VKi ≠ V K2 bo’lsa, ularning orasidagi farqdan hosil bo’luvchi nisbiy sirpanish rinuvchi sirtlarning o’zaro ishqalanishi va natijada eyilishiga olib keladi. Rasmdan ko’rinib turibdiki, VKi = V K2 sharti faqat bitta holatdagina, ya'ni umumiy urinish nuqtasi C NN normal chiziqning markazlar chizig’i O1O2 bilan kesishgan joyidagi P nuqta bilan ustma -ust tushgandagina bajariladi, chunki bunda V1 = V 2 bo’lib qoladi. IX .8 -shakl O1M1P va O2M 2P uchburchaklarning o’xshashligidan Bu yerdan (IX.1 ) (IX.1 ) munosabat tishli ilashishning quyidagi asosiy qonunini ifodalaydi: o’zaro ilashgan tishlarning profillariga ulaming urinish nuqtasidan o’tkazilgan umumiy normal chiziq g’ldiraklarning markazlararo masofasini burchak tezliklarga teskari proportsional bo’l aklarga bo’ladi. Ushbu qonun Villis tomonidan teorema sifatida ochib berilgan. Umumiy normal NN bilan markazlararo O1O2 chiziqning kesishish nuqtasi P g’ildiraklar nisbiy aylanishining oniy markazi bo’lib, ilashish qutbi deb ataladi. Burchak tezliklar ω1 va ω2 orasidagi nisbat ω1/ ω 2 uzatish nisbati deb ataladi va U12 bilan belgilanadi. Ilashish qutbi P ning O1O2 markazlararo chiziqda joylashish holati ω1 va ω2 burchak tezliklarning ham qiymatlariga, ham yo’nalishlariga bog’liq bo’ladi. Agar ω1 va ω2 yo’nalishlari har xil bo’lsa P nuqta IX .8-shakldagiday O1O2 oralig’ida, bir xil bo’lganda esa – O1O2 dan tashqa rida joylashadi. Demak (7.4) ifodani umumiy holda quyidagicha yozish mumkin: (IX.2 ) Uzatish nisbatining doimiylik sharti tishlarining profillari evolventa, tsikloida va doira chiziqlari bilan hosil qilingan ilashishlarda ta'minlanadi. Hozirgi paytda evolventa profilli tishli g’ildiraklar eng ko’p ishlatiladi. Evolventali tishli ilashma: elementlari, xossalari va asosiy o’lchamlari. Aylanaga urinma joylashgan to’g’ri chiziqning sirpanmasdan harakatlanishi nat ijasida undagi istalgan nuqtaning chizgan trayektoriyasi evolventa deyiladi. Bu aylana asosiy aylana, to’g’ri chiziq esa uning yasovchisi deyiladi. To’g’ri chiziq N— N asosiy aylanaga nisbatan sirpanmay harakatlanar ekan ( IX.9 - shakl), undagi ( N1B) kesma uzunligi N1A yoy bo’lagiga teng bo’ladi: P O P O M O M O l 2 1 1 2 2 = P O P O l 2 2 1 −=   P O P O U l 2 2 1 12 = =  

Загрузите документ, чтобы увидеть его полностью.

Похожие