Geometriyadagi ba’zi masalalarni vektorlar usulida yechish






















![3) tekisligiga perpendikulyar bo’lib, (1.2.15-chizma)
1.2.15-chizma. Vektorlarning vektorial ko’paytmasi⃗avektor
ning ⃗bvektor ga vektorial ko’paytmasi:
[⃗
a⃗ b]
ravishda belgilanadi, ya’ni
⃗
c = [⃗ a⃗ b]
Uch vektorning aralash ko’paytmasi
⃗ava ⃗b
vektorlarning vektorial ko’paytmasining uchinchi ⃗c vektorga skalyar
ko’paytmasiga uch vektorning aralash ko’paytmasi deyiladi.
[⃗
a⃗ b]⃗ c ( 1.2 .4 )
⃗ava ⃗b
vektorlarning [⃗a⃗b] vektorial ko’paytmasi vektor bo’lgani uchun, bu
vektorning
⃗c vektorga skalyar ko’paytmasi skalyar bo’ladi, demak, ⃗a,⃗b , ⃗c
vektorlarning (1.2.4) aralash ko’paytmasi skalyardan iborat.
Bu ko’paytma oddiy geometrik ma’noga egadir. Uchala vektor
⃗a,⃗b , ⃗c biror
umumiy O nuqtaga keltirilganda, ularning o’rinlari 1.2.16-chizmadagi kabi bo’lsin.
23](/data/documents/c794ef57-17c8-4988-b65a-95ac8bf7648d/page_23.png)
![1.2.16-chizma. Uch vektorning aralash ko’paytmasi
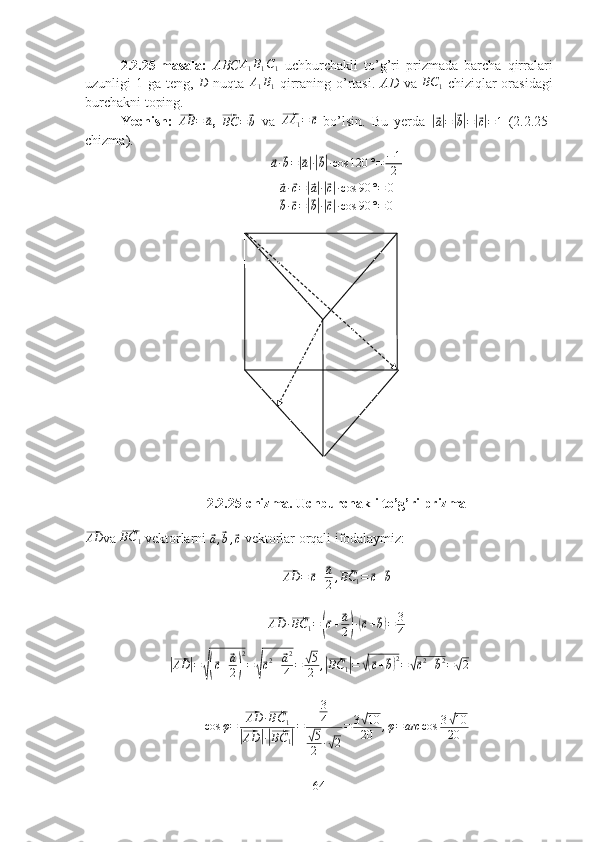
Qirralari berilgan vektorlardan iborat parallelepiped yasaymiz.⃗ava ⃗b
vektorlarda yasalgan parallelogrammning yuzi
|[⃗a⃗b]|
bo’ladi. Ikkinchi tomondan
[⃗a⃗b] vektor ⃗ava ⃗b vektorlarga qurilgan
parallelogrammning tekisligiga perpendikulyar bo’lgani uchun
⃗ c
vektorni [⃗a⃗b]
vektorning yo’nalishiga proyeksiyasini olib, parallelepipedning balandligini hosil
qilish mumkin.
Natijada
V =
[⃗ a⃗ b]⃗ c ( 1.2 .5 )
aralash ko’paytma
⃗a,⃗b , va ⃗ c
vektorlarda yasalgan parallelepipedning hajmini
ifodalaydi.
⃗a,⃗b
, va ⃗c vektorlar o’ng sistema tashkil qilganda, bu ko’paytma musbat va
aks holda manfiy bo’ladi. Shu bilan birga bu yerda
⃗a,⃗b , ⃗c vektorlarni ko’paytirish
tartibiga diqqat qilish kerak, chunki uchala ko’paytuvchidan ikkitasining o’rinlari
o’zaro almashtirilsa, ko’paytmaning ishorasi qarama-qarshi bo’ladi, masalan:
[⃗
a⃗ b]⃗ c = − [⃗ b⃗ a]⃗ c ( 1.2 .6 )
Lekin
⃗a,⃗b , ⃗c vektorlarni doiraviy almashtirganda (ya’ni ⃗a ni ⃗b ga, ⃗b ni ⃗c ga, ⃗c ni ⃗a
ga almashtirganda) aralash ko’paytma o’zgarmaydi, masalan:
[⃗a⃗b]⃗c=−[⃗b⃗a]⃗c=[⃗c⃗a]⃗b(1.2 .7)
chunki bundan asosiy sistema o’zgarmaydi.
Agarda
⃗a,⃗b , ⃗c vektorlar komplanar bo’lsa, bu holda [⃗
a⃗ b] vektor ⃗c vektorga
perpendikulyar bo’lgani uchun
[⃗
a⃗ b]⃗ c = 0 ( 1.2 .8 )
24O](/data/documents/c794ef57-17c8-4988-b65a-95ac8bf7648d/page_24.png)
![geometriya nuqtai nazaridan, albatta shunday bo’lishi kerak, chunki ⃗a,⃗b , ⃗c
vektorlar komplanar bo’lganda parallelepipedning hajmi nolga aylanadi.
Xususiy holda uchala vektordan ikkitasi o’zaro teng bo’lsa, u holda aralash
ko’paytma nolga aylanadi, masalan:
[⃗a⃗a]⃗b=[⃗a⃗b]⃗a=[⃗b⃗a]⃗a=0
Aksincha, (1.2.8) tenglik bajarilganda parallelepipedning hajmi nolga teng
bo’ladi va bu holda: yo uchala vektordan biri nolga teng yoki ulardan ikkitasi
kollinear yoki ular komplanar bo’ladi.
Xulosa
Birinchi bob yordamchi xarakterga ega bo’lib, o’rganilgan mavzuni
yoritishda zarur bo’lgan tushunchalar, vektorlar haqida ma’lumot, vektorlar
yig’indisi, skalyar ko’paytma, vektorlar ko’paytmasiva boshqa bir qancha
ma’lumotlar keltirilgan.
25](/data/documents/c794ef57-17c8-4988-b65a-95ac8bf7648d/page_25.png)














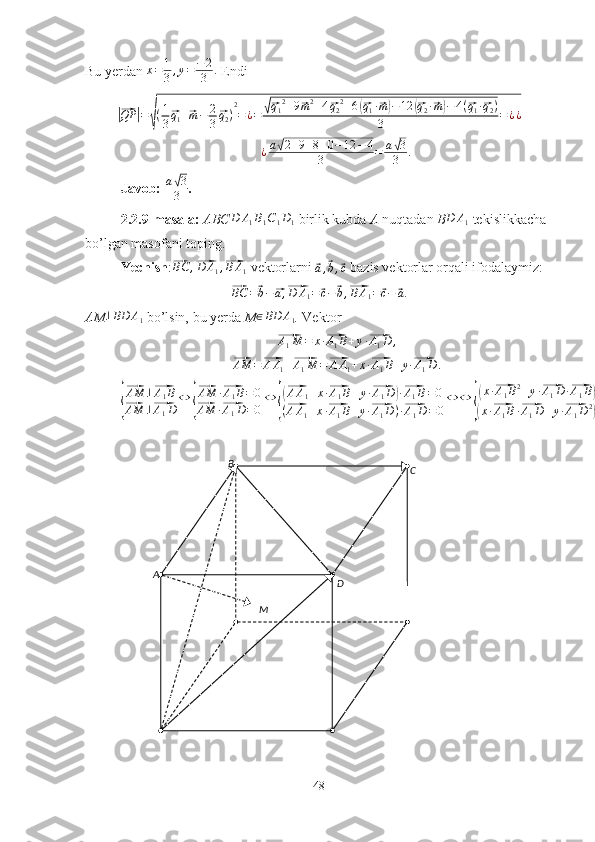


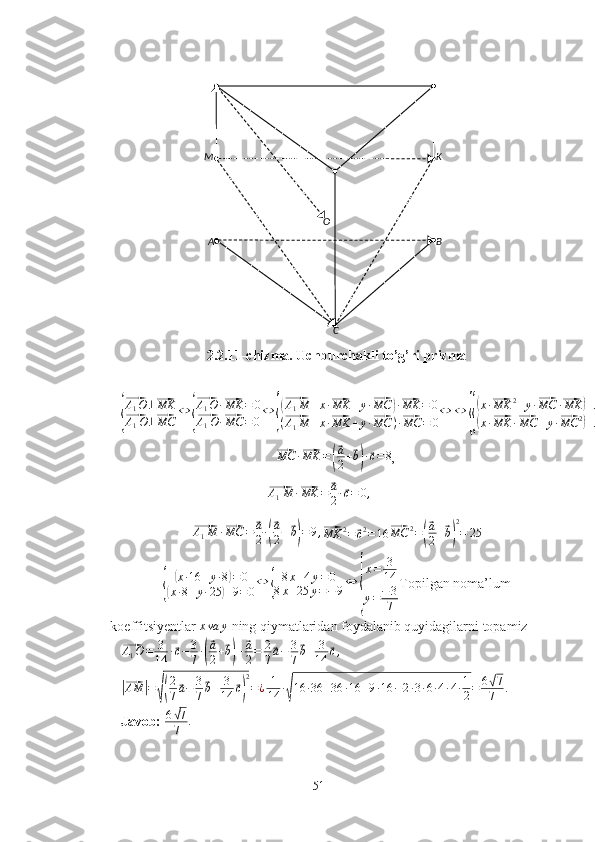
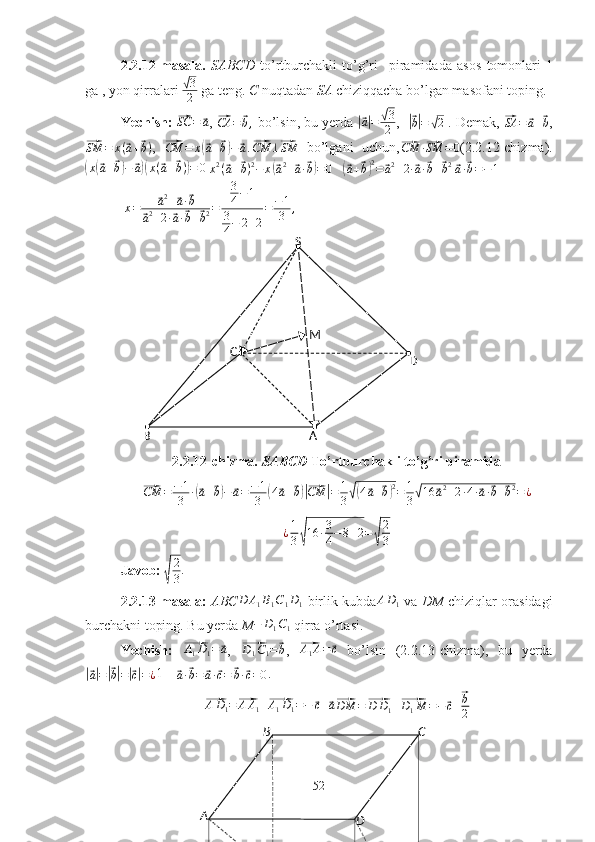
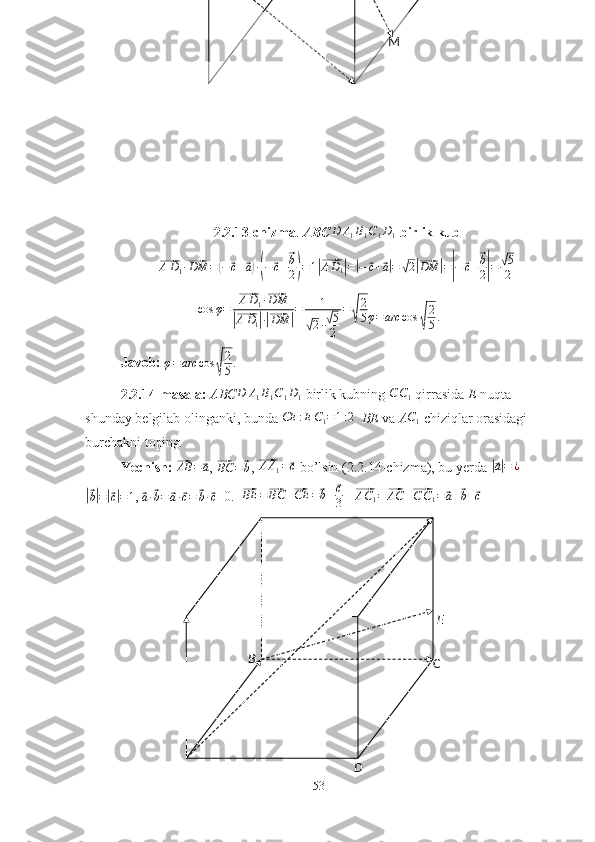













Geometriyadagi ba’zi masalalarni vektorlar usulida yechish Mundarija. Kirish................................................................................................ ........... ....3 I. Asosiy tushunchalar 1.1 Vektorning kelib chiqish tarixi .................................................................7 1.2 Vektorlar haqida umumiy tushunchalar....................................................9 II. Geometriya masalalarini yechishda vektorlarning qo’llanilishi 2.1 Planimetrik masalalarni yechishda vektorlar tadbiqi…………… …….. 28 2.2 Stereometrik masalalarni yechishda vektorlar tadbiqi...........................43 2.3 Vektorlar usulidan foydalanib yechish uchun masalalar …….............. ...75 Xotima ..........................................................................................................79 Foydalanilgan adabiyotlar ..........................................................................80 1
KIRISH Ta’lim va ma’rifat tizimini takomillashtirish,mamlakatimiz kelajagi bo’lgan yoshlarni zamonaviy bilim olishga yo’naltirish,barkamol shaxsini tarbiyalash bilan bog’liq ekanini biz yaxshi anglaymiz. Sh.M.Mirziyoev. O‘zbekiston jahonning taraqqiy etgan mamlakatlari qatoridan o‘rin egallash va uni mustahkam saqlab turish uchun O‘zbekistonda fundamental fanlar jahon andozalari darajasida bo‘lishi kerak. Shu o‘rinda O‘zbekiston Respublikasi Birinchi Prezidenti I.A.Karimovning “O‘zbekiston innovatsion rivojlanish turining hozirgi zamon modeliga o‘tish uchun zarur sharoitlarga ega. Bu model vujudga keltirilgan ilmiy-texnikaviy salohiyatdan keng va samarali foydalanishga, fundamental va amaliy fanning yutuqlarini, chuqur ilm talab qiladigan amaliyotga keng qamrovda joriy etishga, yuqori malakali, iqtidorli kadrlar sonini ko‘paytirishga asoslanadi. Bu mamlakatimiz jahondagi iqtisodiyoti va sanoati rivojlangan davlatlar qatoriga kirib borishining zarur sharti va mustahkam poydevori bo‘lib xizmat qiladi” degan fikrlarini keltirib o‘tish o‘rinli. Respublikamizda “Talim to‘g‘risida”gi qonun va Kadrlar tayyorlash Milliy Dasturini qabul qilinishi, qolaversa, O‘zbekiston Respublikasi Birinchi Prezidenti I. A. Karimovning O‘zbekiston Respublikasi Oliy Majlisi Qonunchilik palatasi va Senatining 2010 yil 27 yanvar kuni bo‘lib o‘tgan qo‘shma majlisidagi “Mamlakatni modernizatsiya qilish va kuchli fuqarolik jamiyati barpo etish – ustuvor maqsadimizdir” hamda Vazirlar Mahkamasining 2010 yil 29 yanvar kuni bo‘lib o‘tgan majlisidagi “Asosiy vazifamiz – Vatanimiz taraqqiyoti va xalqimiz farovonligini yanada yuksaltirish” mavzusidagi ma’ruzalari zamirida ham aynan shu muammoni hal etish ko‘zda tutilgan. Shavkat Mirziyoyevning O‘zbekiston Respublikasi Prezidenti lavozimiga kirishish tantanali marosimiga bag‘ishlangan Oliy Majlis palatalarining qo‘shma 2
majlisidagi nutqida “ Biz yoshlarga doir davlat siyosatini hech og‘ishmasdan, - qat’iyat bilan davom ettiramiz. Nafaqat davom ettiramiz, balki bu siyosatni eng ustuvor vazifamiz sifatida bugun zamon talab qilayotgan yuksak darajaga ko‘taramiz. Yoshlarimizning mustaqil fikrlaydigan, yuksak intellektual va ma’naviy salohiyatga ega bo‘lib, dunyo miqyosida o‘z tengdoshlariga hech qaysi sohada bo‘sh kelmaydigan insonlar bo‘lib kamol topishi, baxtli bo‘lishi uchun davlatimiz va jamiyatimizning bor kuch va imkoniyatlarini safarbar etamiz ” deb ta’kidlagan edi. Biz ta’lim va tarbiya tizimining barcha bо‘g‘inlari faoliyatini bugungi zamon talablari asosida takomillashtirishni o‘zimizning birinchi darajali vazifamiz deb bilamiz. Yosh avlod tarbiyasi haqida gapirganda, Abdurauf Fitrat bobomizning mana bu fikrlariga har birimiz, ayniqsa, endi hayotga kirib kelayotgan o‘g‘il- qizlarimiz amal qilishlarini men juda-juda istardim. Mana, ulug‘ ajdodimiz nima deb yozganlar: “Xalqning aniq maqsad sari harakat qilishi, davlatmand bo‘lishi, baxtli bo‘lib izzat-hurmat topishi, jahongir bo‘lishi yoki zaif bo‘lib xorlikka tushishi, baxtsizlik yukini tortishi, e’tibordan qolib, o‘zgalarga tobe va qul, asir bo‘lishi ularning o‘z ota-onalaridan bolalikda olgan tarbiyalariga bog‘liq”. Qarang, qanday bebaho, oltinga teng so‘zlar! Bugungi kunda yon- atrofimizda diniy ekstremizm, terrorizm, giyohvandlik, odam savdosi, noqonuniy migrasiya, “ommaviy madaniyat” degan turli balo-qazolarning xavfi tobora kuchayib borayotganini hisobga oladigan bo‘lsak, bu so‘zlarning chuqur ma’nosi va ahamiyati yanada yaqqol ayon bo‘ladi. O‘zbekistonning kelajagi, uning istiqboli,birinchi navbatda yoshlar tarbiyasiga, ularni sog‘lom qilib o‘stirishga, milliy g‘oya, milliy mafkura va o‘z vataniga sadoqat ruhida tarbiyalashga bog‘liq bo‘lib, bu murakkab jarayonni muvaffaqiyatli amalga oshirish mustaqil mamlakatning eng dolzarb vazifalaridan biridir. Shuning uchun ham, Prezidentimiz Islom Abdug‘aniyevich Karimovning “Mamlakatimizning istiqboli yosh avlodlarimiz qanday tarbiya topishiga, qanday ma’naviy fazilatlar egasi bo‘lib voyaga yetishiga, farzandlarimizning hayotga nechog‘lik faol munosabati bo‘lishiga, qanday oliy maqsadlarga xizmat qilishiga 3
bog‘liq ekanligini hamisha yodda tutishimiz kerak” deb ta’kidlagani bejiz emas. Shu boisdan ham bugungi kunda yoshlarning ta’lim-tarbiyasi mustaqil O‘zbekistonning davlat siyosatida ustivor ahamiyat kasb etmoqda. Yurtimizning birinchi prezidenti Islom Karimovning “Yuksak ma’naviyat – yengilmas kuch” asarida ta’kidlaganidek, yoshlarimizning ma’naviy olamida bo‘shliq vujudga kelmasligi uchun ularning qalbi va ongida sog‘lom hayot tarzi, milliy va umummilliy qadriyatlarga hurmat- ehtirom tuyg‘usini bolalik paytidan boshlab shakillantirishimiz zarur. Talabalarga bilim berishda zamonaviy ta’lim texnologiyalarining ahamiyati to‘g‘risida so‘z borganda birinchi prizidentimiz I.A.Karimovning “O‘quv jarayoniga yangi axborot va pedagogik texnologiyalarni keng joriy etish, bolalarimizni komil insonlar etib tarbiyalashda jonbozlik ko‘rsatadigan o‘qituvchi va domlalarga e’tiborimizni yanada oshirish, qisqacha aytganda, ta’lim-tarbiya tizimini sifat jihatidan butunlay yangi bosqichga ko‘tarish diqqatimiz markazida bo‘lishi darkor”degan so‘zlarini ta’kidlash o‘rinlidir. Hozirgi kunda jahon tajribasidan ko‘rinib turibdiki, ta’lim jarayoniga o‘qitishning yangi, zamonaviy usul va vositalari kirib kelmoqda va samarali foydalanilmoqda. Bitiruv malakaviy ishining dolzarbligi: vektorlar tushunchasi matematikaning ko’p sohalarida, geometriyada, fizikaviy, mexanikaviy masalalarni yechishda qo’llaniladi. Bitiruv malakaviy ishining maqsadi: vektorlarni geometrik masalalarni yechishda qo’llash. Bitiruv malakaviy ishining vazifalari: Bitiruv malakaviy ishi quyidagi vazifalarni o’z ichiga oladi: 1. Vektorlarga oid ma’lumotlarni o’rganish. 2. Vektorlarni planimetrik masalalarda tadbiq qilish. 3. Vektorlarni stereometrik masalalarda tadbiq qilish. Bitiruv malakaviy ishining o’rganilganlik darajasi: to’liq o’rganilgan. 4
Bitiruv malakaviy ishining predmeti va obyekti: ko’pburchaklar, ko’pyoqlar. Bitiruv malakaviy ishining yangiligi: bitiruv malakaviy ishi referativ xarakterga ega. Bitiruv malakaviy ishining amaliy ahamiyati: bitiruv malakaviy ishidan maktab o’quvchilari, abituriyentlar, akademik litsey va kasb-hunar kolleji talabalari geometrik masalalarni yechishda bilimlarini mustahkamlashda foydalanishlari mumkin. Bitiruv malakaviy ishning hajmi va tuzilishi: BMI kirish, ikki ta bob, beshta paragraf, ikki bobning xulosasi, xotima va foydalanilgan adabiyotlar ro’yxatidan iborat . 5
