Viyetning umumlashgan teoremasi. Kvadrat uchhadni chiziqli ko'paytuvchilarga ajratish dars ish








O’ZBEKISTON RESPUBLIKASI OLIY TA’LIM FAN VA INNOVATSIYALAR VAZIRLIGI MIRZO ULUG’BEK NOMIDAGI SAMARQAND DAVLAT ARXITEKTURA – QURILISH UNIVERSITETI AKADEMIK LITSEY “Tasdiqlayman” O’quv ishlari bo’yicha direktor o’rinbosari ________ F. Xoliqulov ________ 2024-yil SamDU Matematika fakulteti Amaliy matematika yo`nalishi talabasi SamDAQU akademik litsey 104-guruhda ALGEBRA fanidan o`tkazilgan ochiq dars MAVZU: Viyetning umumlashgan teoremasi. Kvadrat uchhadni chiziqli ko'paytuvchilarga ajratish. SAMARQAND-2024 O‘quv predmetining nomi: Algebra OCHIQ DARS ISHLANMASI
O‘ quv m а shg’ul о tid а t а ’lim t ех n о l о giyasi m о d е li Mavzu: Viyetning umumlashgan teoremasi. Kvadrat uchhadni chiziqli ko'paytuvchilarga ajratish. O‘quv soati: 80 - minut O‘quvchilar soni : 12 ta O‘quv mashg‘uloti shakli va turi Amaliy. Yangi bilimlarni egallash bo‘yicha amaliy o‘ quv mashg‘ulot i. M ashg‘ulot rejasi 1 Kvadrat tenglamaning xususiy hollari ; 2 . Viyetning umumlashgan teoremasi ; 3. Chala kvadrat tenglamalar ; O’quv mashg’ulotining maqsadi: Viyetning umumlashgan teoremasi. Kvadrat uchhadni chiziqli ko'paytuvchilarga ajratish haqidagi tushunchalarini va ularni yechish usullari bo’yicha malakalarni shakllantirish . Ta’limiy maqsadi : Kvadrat tenglamalar ustida amallar haqidagi tushunchalarini va ularni yechish usullari bo’yicha ko‘ nikmalarni shakillantirish. Tarbiyaviy maqsadi: O‘quvchilarda t o‘ g‘ri s o‘zlik, bir-birini tushunish, hurmat qilish, misolni yechishda estetik did bilan chiroyli yozish ko‘nikmalarni shakllantirish; Rivojlantiruvchi maqsadi: O‘quvchilarning nutqi, mantiqiy fikrlashi, tasavvuri, irodasi, qobiliyati, ijodiy ishlashini rivojlantirishdan iborat. Pedagogik vazifalar: Pedagogik vazifalar: Kvadrat tenglama haqida tushuncha berish; Kvadrat tenglama yechishning maxsus usullari haqida tushuncha berish; ; O‘quv faoliyatining natijalari : Diskriminant haqida tushuncha berish; Kvadrat tenglamalar yechishning maxsus usullari amallarni bajarish; Viyet haqida tushuncha berish ; Kvadrat tenglama yechishning maxsus usullari Ta’lim usullari Ma’ruza, tushuntirish. Aqliy hujum, ko’rgazmali qurollar Ta’lim shakli Jamoaviy, kichik guruxlar Ta’lim vositalari Darslik, ma’ruza matni, yozuv taxtasi, tarqatma materiallar.
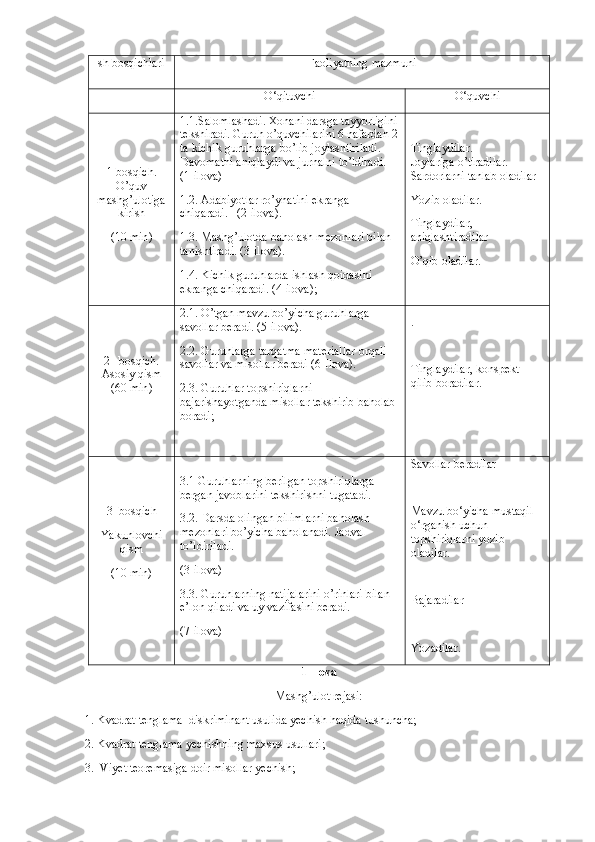
1- Ilova Mashg’ulot rejasi: 1. Kvadrat tenglama diskriminant usulida yechish haqida tushuncha ; 2 . Kvadrat tenglama yechishning maxsus usullari ; 3. V i yet teoremasiga doir misollar yechish ; Ish bosqichlari Faoliyatning mazmuni O‘qituvchi O‘quvchi 1-bosqich. O’quv mashg’ulotiga kirish (10 min ) 1.1. Salomlashadi. Xonani darsga tayyorligini tekshiradi. Guruh o’quvchilarini 6 nafardan 2 ta kichik guruhlarga bo’lib joylashtiriladi. Davomatni aniqlaydi va jurnalni to’ldiradi. (1-ilova) 1.2. Adabiyotlar ro’yhatini ekranga chiqaradi. (2-ilova). 1.3. Ma shg’ulotda baholash mezonlari bilan tanishtiradi. (3-ilova) . 1.4. Kichik guruhlarda ishlash qoidasini ekranga chiqaradi. (4-ilova); Tinglaydilar. Joylariga o’tiradilar. Sardorlarni tanlab oladilar Yozib oladilar. Tinglaydilar, aniqlashtiradilar O’qib oladilar. 2 – bosqich. Asosiy qism (60 min ) 2.1. O’tgan mavzu bo’yicha guruhlarga savollar beradi. (5-ilova). 2.2. Guruhlarga tarqatma materiallar orqali savollar va misollar beradi (6-Ilova). 2.3. Guruhlar topshiriqlarni bajarishayotganda misollar tekshirib baholab boradi; . Tinglaydilar, konspekt qilib boradilar. 3- bosqich Yakunlovchi qism ( 1 0 min) 3.1 Guruhlarning berilgan topshiriqlarga bergan javoblarini tekshirishni tugatadi. 3.2. Darsda olingan bilimlarni baholash mezonlari bo’yicha baholanadi. Jadval to’ldiriladi. (3-ilova) 3.3. Guruhlarning natijalarini o’rinlari bilan e’lon qiladi va uy vazifasini beradi. (7-ilova) Savollar beradilar Mavzu bo‘yicha mustaqil o‘rganish uchun topshiriqlarni yozib oladilar. Bajaradilar Yozadilar.
2 – Ilova Adabiyotlar ro’yxati: 1. Matematikadan mavzulashtirilgan testlar to’plami ю (1996-2007) . 2.F.Xoliqulov M. Jabborov.Q.Janiqulov 3. Jumaniyozov Q.S. Masalalarni turli usullar bilan yechish asosida O’quvchilarning matematik tasavvurinio rivojlantirish. Ma’ruzalar to’plami.-Toshkent: TDPU, 2000.-111-115-b. 3. www. ziyonet.uz 4. mathnet.uz. 5. Abituriyentlar uchun mavzulashtirilgan tetslar to’plami (1996-2003). 3 - Ilova Guruhlar ishini baholash mezonlari:Guruh 1-2 topshiriq uchun Мах балл: 5; 5 ball 3-4 topshiriq uchun Мах балл: 5; 5 ball 5-6 topshiriq uchun Мах балл: 5; 5 ball 7-8 topshiriq uchun Мах балл: 5; 5 ball 9-10 topshiriq uchun Мах балл: 5; 5 ball Qo’shimcha savol Jami Мах балл: 50 ball 1 2 3 4 – Ilova Guruhlarda ishlash qoidasi Sherigingizni diqqat bilan tinglang. Guruh ishlarida o’zaro faol ishtirok eting, berilgan topshiriqlarga javobgarlik bilan yondoshing. Agar sisga yordam kerak bo’sa, albatta guruh a’zolariga murojaat qiling Agar sizdan yordam so’rashsa, albatta yordam bering. Guruhlar faoliyati natijalarini baholashda hamma ishtirok etishi shart! Shuni tushunmog’ingiz lozim: Boshqalarga o’rgatish orqali o’zimiz o’rganamiz; Biz bir kemadamiz: yoki birgalikda suzib chiqamiz, yoki birgalikda cho’kib ketamiz; 5– Ilova. Mavzuning bayoni. Kvadrat tenglama
I. ax 2 +bx+c=0, a≠0 ko'rinishdagi tenglama, bir noma'lumli kvadrat tenglama deyiladi. a - birinchi, b - ikkinchi koeffitsiyent, c - ozod had. Kvadrat tenglama ildizlari formulasi: D=b 2 -4ac ifoda diskriminant deyiladi. 1) Agar D<0 bo'lsa, tenglama yechimga ega bo'lmaydi. 2) Agar D=0 bo'lsa, tenglama ikkita bir xil X=-b/2a yechimga ega. 3) Agar D>0 bo'lsa, tenglama ikkita yechimga ega: Misol. 1) 2x 2 -10x+12=0 kvadrat tenglamada a=2, b=-10, c=12. D=(-10) 2 -4∙2∙12=100-96=4. D>0 demak, tenglama 2 ta yechimga ega: Javob: x 1 =3, x 2 =2 2) 3x 2 +2x+4=0 kvadrat tenglamada a=3, b=2, c=4. D=2 2 -4∙3∙4=4-48=-44. D<0 demak, tenglama yechimga ega emas. 3) x 2 +2x+1=0 kvadrat tenglamada a=1, b=2, c=1. D=2 2 -4∙1∙1=4-4=0. D=0 demak, tenglama bitta yechimga ega: x=-2/2=-1. II. Agar kvadrat tenglamada b yoki c nolga teng bo'lsa, tenglama chala kvadrat tenglama deyiladi. ax 2 +c=0 bo'lsa, x 2 =-c/a. Bunda -c/a<0 bo'lganda yechimga ega. ax 2 +bx=0 bo'lsa, x(ax+b)=0. x 1 =0, x 2 =-b/a yechimga ega. Misol. 1) 2x 2 -8=0 tenglamadan x 2 =8/2=4. bundan x 1 =2, x 2 =-2. 2) x 2 +9=0 tenglamadan x 2 =-9 tenglama yechimga ega emas. 3) 3x 2 +6x=0 tenglamani x(3x+6)=0 ko'rinishga keltirsak, x 1 =0, x 2 =-6/3=-2 yechimlarini topamiz. III. Kvadrat tenglamada birinchi koeffitsiyent birga teng bo'lsa x 2 +px+q=0 bo'ladi. Unga keltirilgan kvadrat tenglama deyiladi. Keltirilgan kvadrat tenglama ildizlari formulasi:
