Kombinatorikaning asosiy qoidasi














KOMBINATORIKA ELEMENTLARI KOMBINATORIKANING ASOSIY QOIDALARI
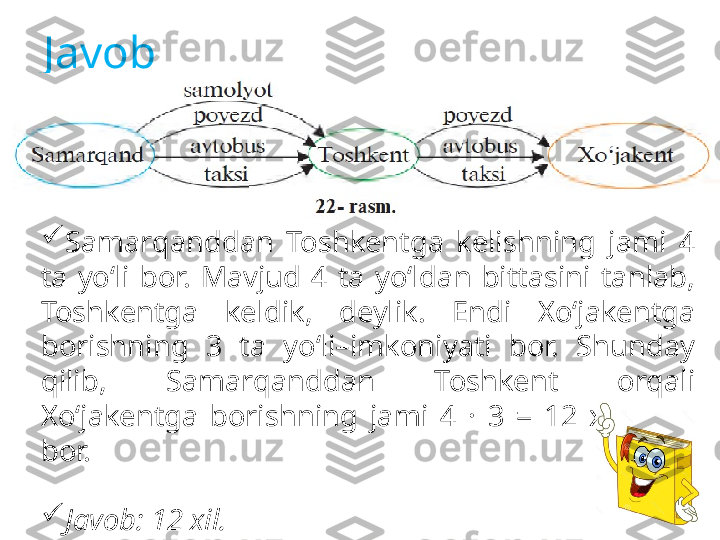
1- masala. Samarqanddan Toshk ent ga 4 xil y o‘l bilan k elish mumk in: samolyot, poyezd, avtobus va yengil mashina(taksi). Toshkentdan Xo‘jakentga 3 xil transport vositasi olib boradi: poyezd, avtobus, taksi. Samarqanddan Xo‘jakentga necha xil usulda kelish mumkin (22- rasm)?
Javob Samarqanddan Toshkentga kelishning jami 4 ta yo‘li bor. Mavjud 4 ta yo‘ldan bittasini tanlab, Toshkentga keldik, deylik. Endi Xo‘jakentga borishning 3 ta yo‘li–imkoniyati bor. Shunday qilib, Samarqanddan Toshkent orqali Xo‘jakentga borishning jami 4 · 3 = 12 xil usuli bor. Javob: 12 xil.
Bu qoida ko‘paytirish qoidasidir va u kombinatorikaning asosiy qoidasi hisoblanadi. Umuman, A shahardan B shaharga kelishning m ta, B dan C shaharga kelishning n ta yo‘li bo‘lsa, u holda A dan C ga kelishning jami m · n ta yo‘li bor, ya’ni A dan C ga m· n xil usuli bilan kelish mumkin.
