tg x va ctgx funksiya



![х у= tg x
0
± π ∕ 6
± π ∕ 4
± π ∕ 3
± π ∕ 2y
x1
- 1
0
2
2
у = tg x
0
≈ ± 0,6
± 1
≈ ±1,7
Не
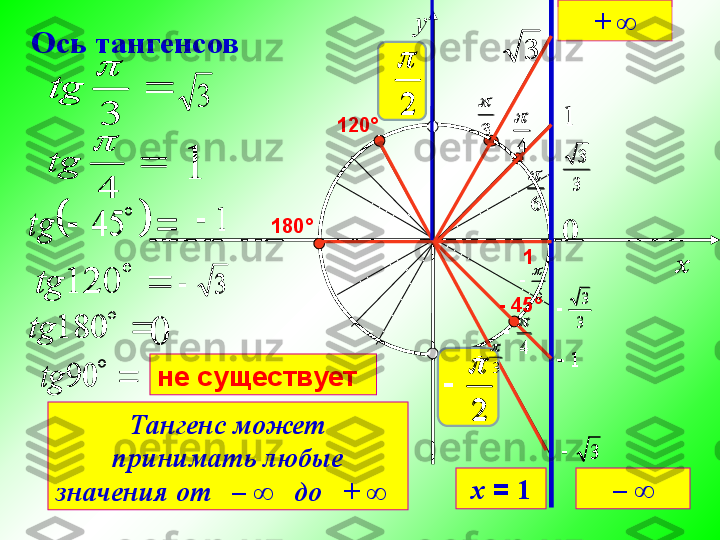
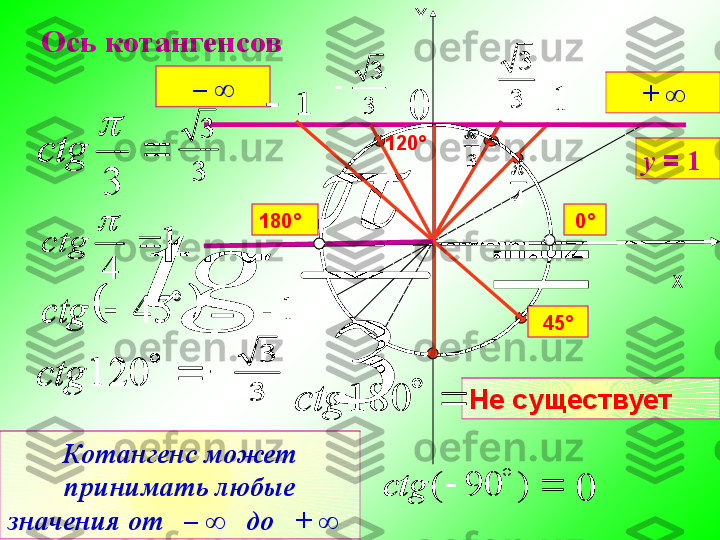
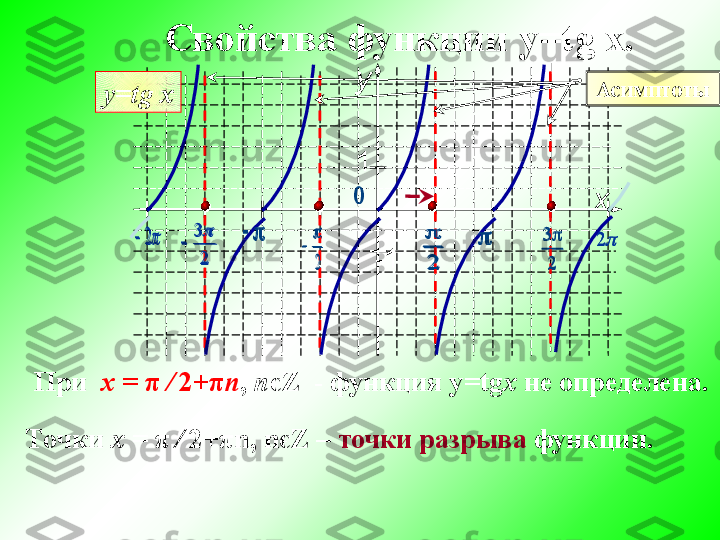
существ.Построение графика функции y = tg x ,
если х Є [
̶ π ∕ 2; π ∕ 2 ]
0
2
2
](/data/documents/c98dba78-3f24-47bf-8d29-0078853c44c2/page_6.png)
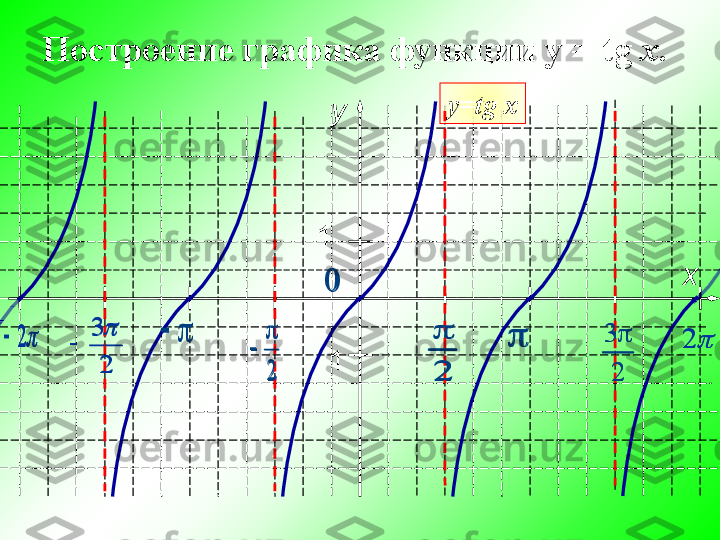
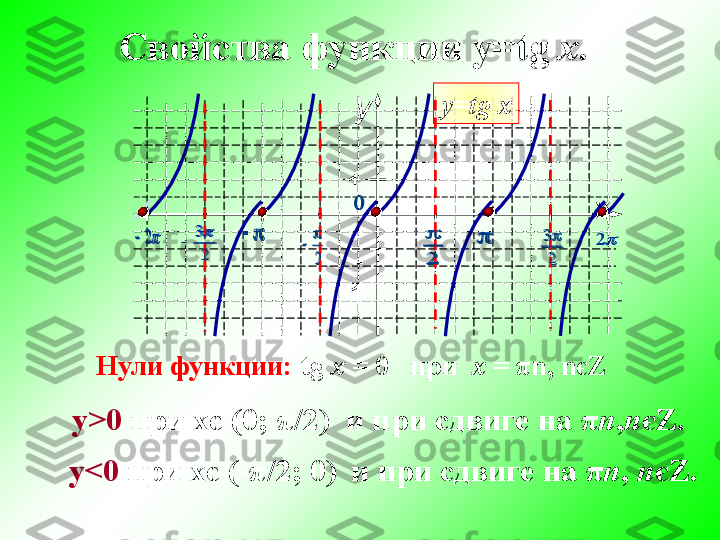

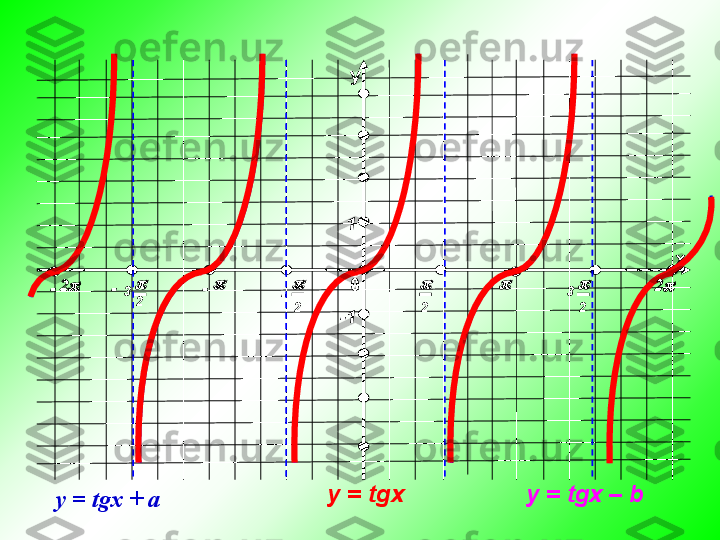
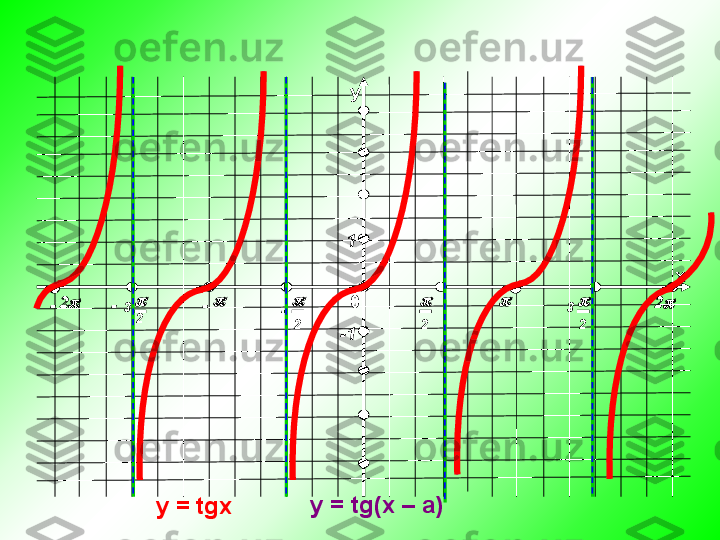
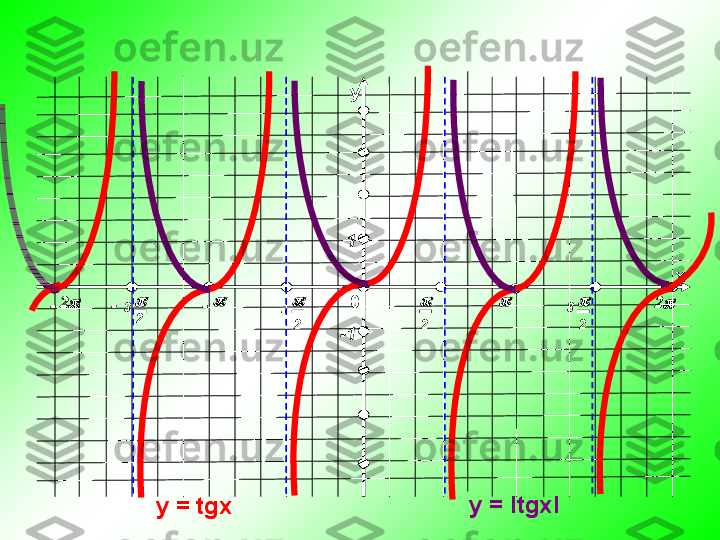

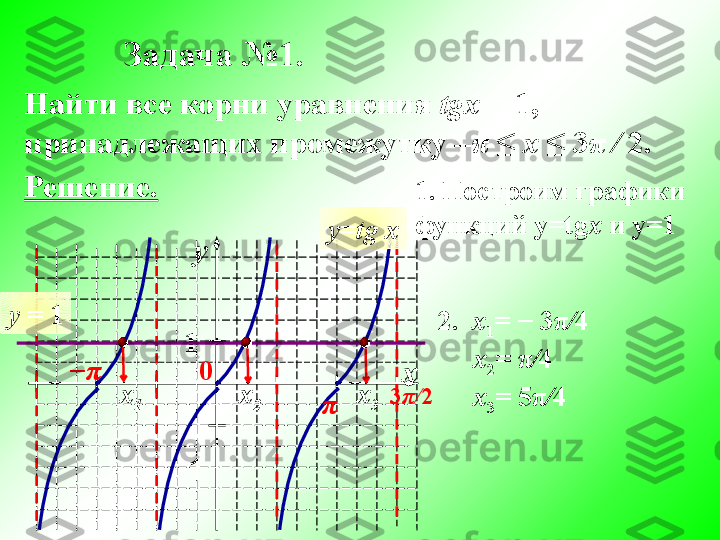
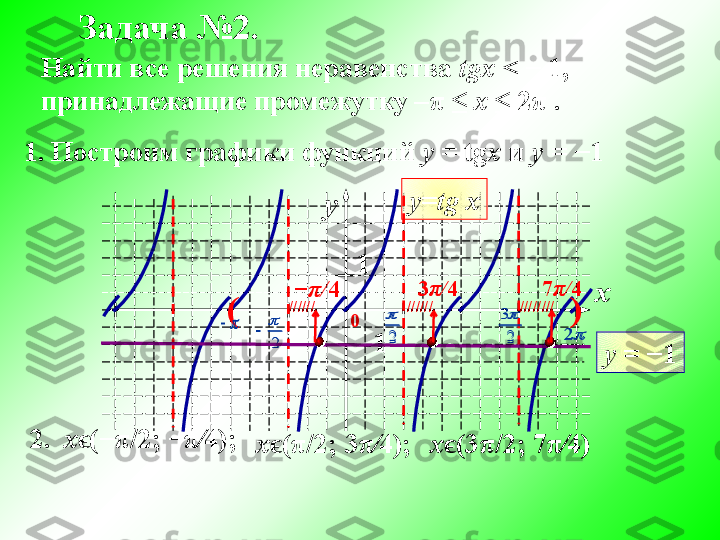
y = tgx va y = ctgx funksiya grafigi va xossalari
Определение Тангенс определён для всех углов α , кроме тех, для которых косинус равен нулюТангенсом угла α называют число, равное отношению sin α к cos α , обозначают tg α , т. е. cos sin tg Z k k , 2 Для любого угла α ≠ π /2 + π k , k Є Z существует, и притом единственный tg α cos sin tg Z k k , 2
x 6 3 3 0 3 3 3 3 1 1 y 3 4 4 6 3 Ось тангенсов 3 tg 3 4 tg 1 45 tg 1 120 tg 3 180tg 0 90 tg не существует 1180° - 45°120° х = 12 2 Тангенс может принимать любые значения от – ∞ до + ∞ – ∞+ ∞ 6 3 3 0 3 3 3 3 1 1 3 4 4 6 3 3 tg 3 4 tg 1 45 tg 1 120 tg 3 180 tg 0 90 tg 2 2
Определение Котангенс определён для всех углов α , кроме тех, для которых синус равен нулюКотангенсом угла α называют число, равное отношению cos α к sin α , обозначают с tg α , т. е. sin cos сtg Z k k , Для любого угла α ≠ π k , k Є Z существует, и притом единственный с tg α sin cos сtg Zkk ,
X0 3 3 3 3 1 1 Y Ось котангенсов 3 tg 1 1 0 Не существует 3 сtg 4 сtg 45 сtg 120 сtg 180 сtg )90(сtg 3 3 3 3 3 4 у = 1120° 180° 0° Котангенс может принимать любые значения от – ∞ до + ∞ – ∞ + ∞ 45° 0 3 3 3 3 1 1 1 1 0 3 сtg 4 сtg 45 сtg 120 сtg 180 сtg ) 90 ( сtg 3 3 3 3 3 4
