Arifmetik amallar


















![α= α
1 × α
2 =( a
1 a
2 – b
1 b
2 ) + (a
1 b
2 + a
2 b
1 )i
kompleks songa aytiladi. Kompleks sonlarni ko’paytirganda i 2
=-1, i 3
= -
i , i 4
= i 2
×i 2
=1, i 5
=i va hokazo, umuman k butun bo’lganda i 4k
=1,
i 4k+1
=i, i 4k+2
=-1 , i 4k+3
=-
i ekanligini e’tiboga olish kerak.
Misol: (5+2i)(3-4i)= 23-14i
(2+i)(2-i)= 4+1=5
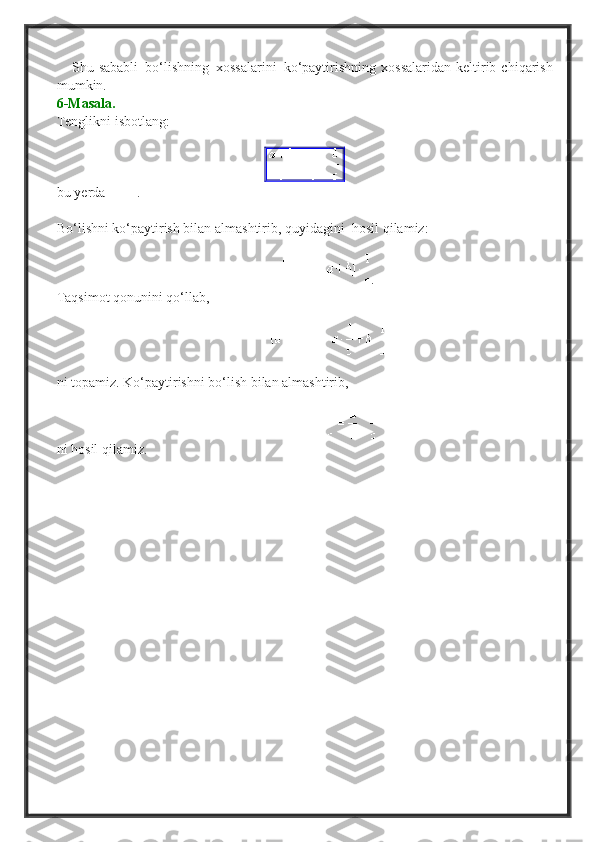
4. Bo’lish amali. . α
1 =a
1 +b
1 i kompleks sonning α
2 =a
2 +b
2 i kompleks songa bo’linmasi
deb α
1 = α× α
2 tenglikni qanoatlantiradigan α kompleks songa aytiladi va u quyidagi
formula bilan topiladi:
Misol:
O’rin almashtirish, gruppalash qonuni kompleks sonlarda ham to’g’ri:
(a+bi)
+ (c+di) = (c+di) + (a+bi)
(a+bi)
· (c+di) = (c+di) · (a+bi)
(a+bi)
+ (c+di) + (e+fi) = (a+bi) + [(c+di) + (e+fi)]](/data/documents/b0bff267-1238-4f7f-a3d5-ab77d111f0b9/page_20.png)






Mavzu: Arifmetik amallar Reja: 1. Arifmetika haqida tushuncha. 2. Arifmetik amallarni o’rgatishda amallar bajarishni umumiy metodikasi . 3. Arifmetik amallarning xossalari . a) Qo’shish va ko’paytirish b) Ayirish c) Bo’lish 4. Arifmetik amallar. a) Butun sonlar ustida b) Ratsional sonlar ustida c) Haqiqiy sonlar ustida d) Kompleks sonlar ustida 5. Ilova
Kirish O’zbekiston Respublikasida shakllangan uzluksiz ta’lim tizimi barkamol shaxs va malakali mutaxassisni tayyorlash jarayonining samarali tashkil etilishini ta’minlashga xizmat qiladi. Uzluksiz ta’lim tizimi doirasida faoliyat olib boruvchi ta’lim muassasalari ilg’or, demokratik hamda insonparvar g’oyalarga tayangan, hamda yangicha mazmunga ega bulgan ta’lim jarayonini tashkil etishda muhim o’rin tutadi. «Kadrlar tayyorlash milliy dasturi»da ta’kidlanganidek, ta’limning yangi tizimi va mazmunini shakllantirish uchun «ilg’or texnologiyalarni hamda o’quv-tarbiyaviy jarayonning didaktik ta’minotini yaratish» talab etiladi. Bu muhim vazifaning ijobiy hal etilishi ta’lim jarayonini tashkil etishga nisbatan yangicha yondashuvni taqozo qiladi. O’zbekiston Respublikasining mustaqilligi sharoitida uzluksiz ta’lim tizimining barcha bosqichlarida ta’lim jarayonining samaradorligini oshirishga xizmat qiluvchi omillarni izlab topish , bu borada eng maqbul omil deb topilgan yangi pedagogik texnologiyalarni umumiy o’rta ta’lim kasb-hunar kollejlari, akademik litseylari va oliy o’quv yurti faoliyatlariga tatbiq etish borasida amaliy harakatlarni olib borish maqsadga muvofiq deb hisoblanmoqda. Umumiy o’rta ta’lim kasb-hunar kollejlari, akademik litsey va oliy o’quv yurtlarida turli o’nalishlarda malakali kadrlarni tayyorlash davrning o’ta muhim talabi bo’lib, bu borada barcha imkoniyatlarni ishga solish alohida dolzarblik kasb etadi. Ta’lim – tarbiya jarayoni sifati va samaradorligini oshirish kelgusi taraqqiyotimizning asosi ekanligi ma’lum. Bu haqda Prezidenttimizning quyidagi so’zlari ibratlidir: “Shuni unutmasligimiz kerakki, kelajagimiz poydevori bilim dargohlarida yaratiladi, boshqacha aytganda, xalqimizning ertangi kuni qanday bo’lishi farzandlarimizning bugun qanday ta’lim va tarbiya olishiga bog’liq. Axborot oqimi keskin ortgan,turli yangiliklar hayotimizga shitob bilan kirib kelayotgan davrda mustaqil tanqidiy fikrlash ko’nikmalariga ega bo’lgan,yangilikni o’rganishga doim tayyor bo’lgan, hamkorlikdan cho’chimaydigan , muloqotga erkin kirisha oladigan shaxsni tarbiyalash ta’lim-tarbiya jarayonining asosiy maqsadi bo’lishi kerak va bu borada ta’limda yangi texnologiyalarning qo’llanishiga yo’l ochilishi maqsadga erishish yo’lidagi to’g’ri qadamdir. Hozirgi kunda yangi texnologiya elementi bo’lgan interfaol usullardan keng foydalanilmoqda. Boshlang’ich sinf matematik darslarida ilg’or pedagogik texnologiyadan foydalanib dars o’tilsa, o’qitish jarayoni takomillashadi. Kurs ishi dolzarbligi ana shu bilan asoslanadi. Kurs ishi maqsadi: Boshlang’ich sinflarda arifmetik amallarni o’rgatishda pedagogik texnologiyalardan foydalanish pedagogik asoslarini ishlab chiqish. Kurs ishi obyekti: Umumiy o’rta ta’limning boshlang’ich sinflaridagi o’quv-tarbiyaviy jarayoni. Kurs ishi predmeti: Boshlang’ich sinflarda arifmetik amallarni o’rgatishda pedagogik texnologiyalardan foydalanish. Kurs ishi tuzilishi: Kurs ishiga kirish, murakkab reja, xulosa, foydalanilgan adabiyotlar ro’yxatidan iborat.
1. Arifmetika haqida tushuncha. Arifmetika (lotincha. arithmos — son) — sonlar va sonli to plamlarda berilgan ʻ amallar (qo shish, ayirish, ʻ ko paytirish ʻ va bo lish ʻ )ni o rganuvchi ʻ fan . Sonlar yordamida beriladigan misol va masalalar o ziga xos sodda usullarda yechiladi va kelgusida mat. ni ʻ chuqur o rganishga ʻ zamin bo ladi. Arifmetika deganda ʻ son tushunchasining paydo bo lishi va rivojlanishi, hisoblash usullari va hisoblash qurollari takomillashuvi va turli ʻ tarzdagi sonlar bilan amallar bajarish tushuniladi. Sonlar bilan mantiqiy mulohazalar yuritishga urg u ʻ berilganda nazariy Arifmetika tushunchasi ishlatiladi. Butun sonlarning xususiyatlari sonlar nazariyasida o rganiladi. Arifmetika tushunchasi har xil buyumlar, ʻ narsalar ustida amallar bajarish zaruriyati tug ilganda ham ishlatiladi. ʻ Arifmetika algebra bilan uzviy bog liq. ʻ Arifmetika qadimda odamlar barmoklari yordamida sanash va hisoblashni boshlagan paytlarda paydo bo lgan. Keyinchalik hisoblash va sodda ʻ o lchov ʻ ishlarini amalga oshirish natijasida Arifmetika tez rivojlandi. Ayniqsa, pul paydo bo lgandan so ng pul ʻ ʻ hisobi, i. ch. vositalarining ko payishi, boshqa fanlarga tatbiq qilinishi tufayli ʻ Arifmetika fan sifatida shakllandi. Arifmetika rivojlanish jarayonining eng muhim bosqichlari Hindiston madaniyati taraqqiyoti bilan bog liq. ʻ O rta dengiz ʻ atrofidagi davlatlarning juda ko p qismida, G arbiy Osiyodan tortib to Hindistongacha, Arifmetika ʻ ʻ va umuman mat. ning rivojlanishiga katta ta sir ko rsatgan ʼ ʻ o rta asr ʻ sharqi olimlari uz tarjimalari va asarlarida yunon matematiklari merosini saqlabgina qolmay, hindlarning yutuqlarini targ ib etish bilan cheklanmay, ularni ʻ yana ham boyitdilar. Muhammad al- Xorazmiy Arifmetikaga doir asar yezdi. Bu asarda Arifmetika izchil bayon qilingani uchun u madrasalarda mat. dan asosiy qullanma bo lib kelgan. Arifmetik amallarni ʻ bajarishda hind hisob tizimi (unli sanoq tizi-mi)ga asoslangan yangi usullar 10-a. da Yevropaga tarqala boshlaydi. Yevropaliklarga arifmetik amallarni ishlatish usullari, malakasi hindlardan utgan bo lsa ham bu ʻ jarayon al-Xorazmiyning lotin tiliga tarjima qilingan Arifmetika qo llanmasi yordamida amalga oshirilgan. Bu ʻ asarning usha davrdagi tarjimasi hozirgacha saqlanib qolgan.
2. Arifmetik amallarni o’rgatishda amallar bajarishni umumiy metodikasi I nterfaol metod - ta’lim jarayonida o’quvchilar hamda o’qituvchi o’rtasidadagi faollikni oshirish orqali o’quvchilarning bilimlarni o’zlashtirishini faollashtirish, shaxsiy sifatlarini rivojlantirishga xizmat qiladi. Interfaol metodlarni qo’llash dars samaradorligini oshirishga yordam beradi. Interfaol ta’limning asosiy mezonlari: norasmiy bahs – munozaralar o’tkazish, o’quv materialini erkin bayon etish va ifodalash imkoniyati,o’quvchilar tashabbus ko’rsatishlariga imkoniyatlar yaratilishi, kichik guruh, sinf jamoasi bo’lib ishlash uchun topshiriqlar berish va boshqa metodlardan iborat bo’lib, ular ta’lim – tarbiyaviy ishlar samaradorligini oshirishda o’ziga xos ahamiyatga ega. Hozirda ta’lim metodlarini takomillashtirish sohasidagi asosiy yo’nalishlardan biri interfaol ta’lim va tarbiya usullarini joriy qilishdan iboratdir. Barcha fan o’qituvchilari shu jumladan boshlang’ich sinf o’qituvchilari ham dars mashg’ulotlari jarayonida interfaol metodlardan borgan sari keng ko’lamda foydalanmoqdalar. Interfaol metodlarni qo’llash natijasida o’quvchilarning mustaqil fikrlash, tahlil qilish, xulosalar chiqarish, o’z fikrini bayon qilish, uni asoslangan holda himoya qila bilish, sog’lom muloqot, munozara, bahs olib borish ko’nikmalari shakllanib, rivojlanib boradi. Interfaol degani, o’qituvchi va o’quvchilar orasida o’zaro hamkorlik tufayli dars samaradorligini oshadi, yangi darsni o’quvchi mustaqil harakat, mulohaza, bahs- munozara orqali o’rganadi, qo’yilgan maqsadga mustaqil o’zi darsda o’quvchi faol ishtirok etgan holda kichik guruhlarda javob topishga harakat qiladi,ya’ni ham fikrlaydi , ham baholaydi, ham yozadi, ham gapiradi, ham tinglaydi, eng keragi o’zi faol ishtirok etadi. Interfaol usullarining negizidagi topshiriq mazmunini anglab yetgan o’quvchilar ta’lim jarayoniga o’zlari bilmagan holda qiziqish bilan kirishib ketadilar. “ Aqliy hujum” texnologiyasini qo’llash bir muammoni hal qilish yo’lidan turlicha va iloji boricha ko’proq taklif, fikr – mulohazalarni yig’ishdan iborat. Avvaliga har qanday takliflar qabul qilinadi. Keyin esa, ularning ichidan eng ma’qulini tanlab olinadi. Bu metodni qo’llashda eng nozik tomoni hamma takliflarni “Eslab” qolishdir. Shuning uchun ularni yozib borish kerak bo’ladi. O’qituvchi ularni shartli belgilar va qisqartirishlar bilan doska yoki vatman qog’ozga yozib boradi. Masalan: 3 – sinfda mavzuga oid quyidagi mashqni hal qilish yuzasidan hamma takliflarni yig’ish mumkin. manfiy butun sonlar ustida arifmetik amallarni o’rgatish metodikasi O'quvchilarni matematikadagi arifmetik amallarni bajarishga o'rgatish metodikasi. Bu mavzu ustida ishlashda o'qituvchi oldida turgan asosiy maqsadlar quydagilardan iborat: 1) O'quvchilarni qo'shish va ayirish , ko'paytirish va bo'lish amallarining mazmuni bilan tanishtirish; 2) Hisoblash usullaridan O'quvchilarni o'nlik foydalanishlarini ta'minlash;
a) sonni qismlari bo'yicha qo'shish va ayirish usuli. b) Yig'indining o'rin almashtirish xossalaridan foydalanish qo'shish usuli. c) sonlarni ayirishda qo'shishning tegishli holini bilishdan yoki yig'indi va qo'shiluvchilardan biri bo'yicha ikkinchi qo'shiluvchilarni topish malakasidan foydalanadigan holda yig'indi bilan qo'shiluvchilar orasida bog'lanishlarni bilganlikda asoslanib ayirish usuli. 3) Qo'shish va ayirish, ko'paytirish va bo'lish ko'nikma, malakalarni shakllantirish. Qo'shish va ayirishni o'rganish ishini o'zaro bog'langan bir nechta bosqichga bo'lish mumkin. O'quvchilarda og'zaki va yozma ko'nikmalarni tarkib toptirish matematika dasturining asosiy yo'nalishlardan biridir. Arifmetik amallarni o'rganishdan oldin bolalar ongiga uning ma'nosini, mazmunini yetkazish kerak. Bu vazifa turli xil amaliy ishlarni bajarish asosida o'tkaziladi. U: "o'nlik" mavzusini qo'shish va ayirish amallarning ma'nosi ikki to'plam elementlarini birlashtirish va to'plamdan uning qismlarini ajratish kabi amallar yordamida olib boriladi .Ko'paytirishni uning komponentlari bilan natijasi orasidagi bog'lanishlarni o'rganish asos bo'lib hizmat qiladi. Demak, o'qitishning 1-bosqichida abstrakt bo'lgan narsa navbatdagi bosqichda yanada abstraktroq bilimlarni shakllantirish uchun aniq asos bo'lib hizmat qiladi. Turli hisoblash usullarining o'zlashtirilishi uchun dasturda arifmetik amallarning ba'zi muhim xossalari va ulardan kelib chiqadigan natijalar bilan tanishtirishni nazarda tutadi. Dasturda arifmetik amallarning xossalarini o'rganishdan tashqari arifmetik amal hadlari va natijalari orasidagi bog'lanishlarni ham ko'zda tutadi. Bu ish amallarni, tenglamalarni tekshirishda muhim ahamiyatga ega. Masalan: 6x4=24 bo'lsa, uni bo'lishga bog'lab 24:6=4; 24:4=6 kabi holler hosil qilinadi. Muhim vazifalaridan biri hisoblash ko'nikmalarni shakllantirishdir. Og'zaki va yozma usulda hisoblashlar sinflarning har bir mavzusida o'z aksini topgan. Masalan: og'zaki 276 + 432 = (200+400) + (70+30) + (6+2) = 600+100+8 =708 Yozma: Og'zaki hisoblashlarning asosiy ko'nikmalari Iva2- sinflarda shakllanadi. Og'zaki hisoblash usullari ham, yozma hisoblash usullari ham amallar xossalari va ulardan kelib chiqadigan natijalarni amallar kompanentlari bilan natijalari orasidagi bog'lanishlarni bilganlikka asoslanadi. Yozma va og’zaki hisoblashda pedagogik texnologiyadan foydalanish
