BOSHLANG’ICH SINF O’QUVCHILARIGA ENG SODDA GEOMETRIK SHAKLLARNI O’RGATISHDA ZAMONAVIY TEXNOLOGIYALARNI QO’LLASH

![2
KIRISH
O ’zbekiston Respublikasi Vazirlar Mahkamasi tomonidan tasdiqlangan
“Davlat ta ’lim standarti t o’g’risidagi Nizom ”ga binoan umumiy o’rta ta ’lim, shu
jumladan, boshlang ’ich ta ’lim bosqichi uchun ham alohida -alohida davlat ta ’lim
standarti talablari va me ’yoriy k o’rsatkichlari belgilab q o’yadi.
“Ta ’lim t o’g’risida ”gi Qonunda ta ’kidlanganidek: “Maktabning birinchi sinfiga
bolalar olti -yetti yoshdan qabul qilinadi. “Boshlang ’ich ta ’lim konsepsiyasi ”da
e’tirof etilganidek, olti yoshga t o’lgan har qanday bola aqliy, ruhiy hamda jisminiy
jihatdan maktabda o’qish uchun tayyor b o’lganida, maktabning moddiy -texnik
bazasi bunday bolalarga ta ’lim berish uchun yetarli deb hisoblanganda ha mda
o’qituvchilar pedagogik va psixologik jihatdan olti yoshli bolalarni o’qitishga qodir
deb topilganda maktabga qa bul qilinadilar. Prezidentimiz SH.M.Mirziyoyev
ta ’kidla ganidek: “Boshlang ’ich ta ’lim o’qish, yozish, sanash, o’quv faoliyatining
asosiy malaka va k o’nikmalari, ijodiy fikrlash, o’zini -o’zi nazorat qilish uquvi, nutq
va xulq -atvor madaniyati, shaxsiy gigiyena va sog ’lom turmush tarzi asoslarining
egallab olishini ta ’minlashga da ’vat etilgan. Shunday ekan, ushbu asosda
boshlang ’ich sinflarda o’quvchilarning umum madaniy va axloqiy k o’nikmalari,
dastlabki savodxonlik malakalari shakllantirilishi lozim ”.[I.6 .56] Boshlang ’ich
ta ’lim jarayoni bolalarning mantiqiy tafakkur qila olish salohiyati, aqliy rivojlanishi,
duyoqarashi, kommunikativ savodx onligi va o’z- o’zini anglash salohiyatini
shakllantirishga, jismonan sog ’lom b o’lishga, moddiy borliq g o’zalliklarini his eta
olishga, g o’zallik va nafosatdan zavqlana olish, milliy urf -odatlarni o’ziga singdirish
va ardoqlash, ularga rioya qilishga o’rga tadi.Boshlang ’ich ta ’lim bosqichi oldiga
qo’yilgan vazifalarning bajarilishini nazorat qilish orqali amalga oshiriladi. Ta ’lim
standarti asosida boshlang ’ich sinf o’quvchilaridan standartda belgilab q o’yilgan
ko’rsatkichga erishishni talab qiladi va o’z na vbatida, bu k o’rsatkichlarga erishish
uchun zarur b o’lgan ta ’limiy xizmatlar va vositalar bilan ta ’minlaydi. Boshlang ’ich](/data/documents/8f6d45a3-c2a8-4703-b91f-ce62dd3f391f/page_2.png)



















![22
– Ikki t o’g’ri burchagi b o’lgan t o’rtburchakni toping. Ikki t o’g’ri burchakli
to’rtburchakni k o’rsating va t o’g’ri b o’lgan balandligini yonidan b o’yang.
– Uchta t o’g’ri burchagi b o’lgan k o’pburchakli figurani t oping. ( O ’quvchilar
bunday t o’rtburchaklarning hamma b o’lagi t o’g’ri ekanligini anglaydilar).
– To’rt burchagi t o’g’ri b o’lgan t o’rtburchaklar t o’g’ri burchakli t o’rtburchaklar
deyiladi. Bolalar t o’g’ri burchaklarning balandligi yaqinini b o’yaydilar va
o’qit uvchiga k o’rsatadilar.
O ’quvchilar t o’g’ri burchakli t o’rtburchaklarning muhim va muhim b o’lmagan
sifatlarini anglab olishlari uchun ba ’zi vaqtlar dars mashg ’ulotlari davomida o’yin
sifat mashqlarni bajarishlari mumkin. Masalan: »Ortiqcha figurani olib tas hla»
mashqida bolalar t o’rtburchaklarning muhim va muhim b o’lmagan belgilarini
topishlari uchun amaliy k o’nikma beradi.
Bolalarga har xil materiallardan yasalgan va turli ranglarga b o’yalgan
ko’pburchaklar namoyish etiladi.
– X o’sh, bu figuralarning qaysi belgisi barchasi uchun umumiydir? (Hammasi
to’g’ri burchakli k o’pburchaklardir).
– Qaysi figura ortiqcha?
– Nega? (1,2,3,5 figuralarda t o’rtta tomon bor). O ’qituvchi bu figurani olib
tashlashni taklif etadi.
– Qolgan figuralarning o’zaro farqi nimada?
– Bu figural arning umumiy sifatlari nima? (ularning ranglari turlicha, turli
materialdan, qog ’ozdan va kartondan yasalgan).
– Bu figuralar qanday nomlanadi? (t o’g’ri burchakli t o’rtburchaklar).
– Nega olib tashlangan figurani t o’g’ri burchakli t o’rtburchak deb atash
mumki n emas? (chunki, uning 6ta tomoni bor -to’g’ri burchaklarda esa 4 tomon va
4 burchak b o’ladi) .
Bunday mashqlar bolalar ongida eng muhim tushuncha -to’g’ri t o’rtburchak
belgilarini mustahkamlaydi .[II.1 9. 37]
Birinchi sinf o’quvchilari bu tushunchani chuqurroq tushunib olishlari uchun
shunday o’yin o’tkazish mumkin.](/data/documents/8f6d45a3-c2a8-4703-b91f-ce62dd3f391f/page_22.png)






![29
olishmaydi. Kichik yoshdagi o’quvchilarning esa bunga kuchalri yetmasligi
aniq .[II.20.47]
Matematika ta ’lim boshlang ’ich bosqichidagi yana bir muhim xususiyat shuki,
bu asosan an ’anaviy kurslarga ta aluqli b o’lib, bu yerda faqat geometriya elementlari
o’rganiladi. Birinchi qarashda bu bilan geometrik tushunchalar orasida hech qanday
aloqa va munosabat b o’lmaydigandek k o’rinadi. Haqiqatda esa bunday emas “I-IV
sinflarda matematik ta ’lim metodikasi ” o’quv q o’llanmasida k o’rsatiladiki,
geometrik materialning darsliklarda amalga oshirilgan dasturga kiritilgan asosiy
mazmuni “geometrik bilim -tasavvurlarning yetarlicha t o’liq sistemasini
shakllantirishga y o’naltirilgan b o’lib, bu (mazmunga) geometrik figural ar obrazlari,
ularning elementlari, figuralar orasidagi munosabatlar kiritilgan “. Bu narsa o’qitish
amaliyotida a lbatta hisobga olinishi kerak.
Barcha kichik sinflar o’qituvchilari asosiy geometrik tushunchalarga I -IV
sinflarda o’rganiladigan ixtiyoriy ge ometrik obyektlarni tushunadilar, buning
o’rniga ular eng sodda geometrik figuralar haqida gapirishlari kerak. Bu bilan ular
tomonidan nazariyani qurishning aksoimatik metodini bilmasliklari sabab b o’ladi,
bu esa geometrik materialni bayon etishda ketma -ke tlilik va sistemalilikning
buzulishiga olib keladi. Bunga misollar k o’p. Masalan, uchburchak tushunhchasini
shakllantirayotib bolalar ungacha kesma tushunchasi bilan tanishmaganlari uchun
o’qituvchi uchburchak tomonlarini t o’g’ri chiziqlar deb atab o’ziga
“kelishuvchilikka ” yo’l q o’yadi. Aks holda qanday qilib bu holda ishlatilayotgan
termini cheksizlik xossalari bilan muvofiqlashtirsin. Yoki o’tkir va o’tmas burchak
tushunchalari t o’g’ri burchakni qaralmagan holda kiritiladi .[II.1 9.67]
O ’quvchilarni ichki chizilgan aylanalar bilan tanishtirar ekan o’qituvchi
shunday tushuntiradi, ichki chizilgan aylana figuraning ichidan hamma tomonlarga
tegib turishi kerak. Medianalar kesishgan nuqta faqat teng tomonli uchburchak
uchun ichki chizilgan aylana markazi b o’lad i, chunki bunday uchburchakda mediana
bissektrisa ham b o’ladi. Uchburchakka ichki chizilgan aylana markazi - bu
bissektisalar kesishgan nuqtadir. O ’qituvchi tushuntirishlaridagi bunday terminlar
ko’pligi, ba ’zilarini o’quvchi umrida birinchi bor eshitishlar i ham b o’lishi munkin.](/data/documents/8f6d45a3-c2a8-4703-b91f-ce62dd3f391f/page_29.png)










![40
kattalikdagi, rangdagi, k o’rinishdagi ( o’tkir burchakli, o’tmas burchakl i, teng yonli,
teng tomonli, turli tomonli) uchburchaklarni o’quvchilarga k o’rsatib, ularning
muhim b o’lmagan xossalari (turli xil materiallardan yasalganligi, rangi, katta -
kichikligi, turli k o’rinishga ega ekanligi)dan abstraktlashib, uchburchak uchun
as osiy muhim xossalar bu uning uchta uchi, uchta tomoni va uchta burchagi
mavjudligi ekanligiga e ’tibor qaratishi kerak b o’ladi .[II.1 8. 89]
Metodik q o’llanmalarda bu ishni quyidagicha amalga oshirish tavsiya etiladi;
sinfga olib kirilgan har xil materiallardan qilingan turli xil rangdagi, kattalikdagi,
ko’rinishdagi uchburchaklarni o’quvchilarga k o’rsatib, o’qituvchi: «Bular
uchburchaklar. Ular bir -birlaridan rangi, katta -kichikligi, k o’rinishi bilan farq qilsa
ham, ularning hammasi bir xilda «uch burchaklar» deb ataladi. Kim aytadi, nega bu
figuralar (barcha olib kirgan uchburchaklarni k o’rsatadi) uchburchak deyiladi?»
(Chunki bularning uchtadan burchagi bor). O ’qituvchi k o’rsatib turib gapiradi: «Bu
uchburchakning tomoni, bu uchburchakning uchi. Uchburchakning nechta tomoni
bor, nechta uchi bor?» O ’quvchilar bu savollarga javob berish natijasida
uchburchakning uchta tomoniligini anglab yetadilar. Shundan keyin o’quvchilarning
o’zlaridagi uchburchak modellarida uchburchak elementlarini ajratishadi . Bunda
o’quvchilar uchburchakning uchi bu nuqta ekanligini, uchburchakning tomoni esa
kesma ekanini aniq tushunib olishlari muhimdir.
Uchburchakning yana bir elementi -burchagi bilan tanishtirishda o’quvchilar
birinchi marta burchak haqida tasavvurlarga eg a b o’ladilar va bunda burchak
uchburchakning «uzib olingan burchagi» sifatida talqin etiladi.
Shuning uchun ham o’qituvchi uchburchak burchagini k o’rsatish bilan bir
qatorda (k o’rsatkichning bir uchini uchburchak uchiga q o’yib, uni burchakning bir
tomonida n ikkinchi tomonigacha burib boriladi) katta k o’rsatmalilik uchun
uchburchakning bir qismini -uning burchagini uzib olishi kerak.
O ’quvchilar o’zlari qog ’ozdan, plastilin va ch o’plardan foydalanib,
uchburchaklar modellarini yasashi, daftarlarida uchburchak chizishi va ularni
bo’yashi, boshqa geometrik figuralar ichida uchburchaklarni ajratishga doir
mashqlarni bajarishlari muhim ahamiyaitga ega.](/data/documents/8f6d45a3-c2a8-4703-b91f-ce62dd3f391f/page_40.png)

![42
K o’pburchaklarning modellaridan foydalanib, figuralarni klassifikatsiya
qilishga doir turli xil mashqlarni bajarish mumkin. Agar dastlab bu mashqlar
belgilarni (alomatlarni) ajratishga qaratilagn b o’lsa, masalan:
A) Bu mashqlar bir -biridan nimasi bila n farq qiladi? [13, 8-mashq]
B) Bu yerda qaysi k o’pburchak y o’q b o’lsa, uni daftaringizga chizing. [1 4,
9-mashq]
V) Shakllarni bir s o’z bilan ayting, bunda t o’rtbuchak nechta? Qaysi shakllar
ikkitadan t o’g’ri burchakka ega? [1 4, 10 -mashq]
Chizmaga qarang va undagi shakllar nima deb atalishini a yting?
G) To’rtburchaklar orasidan to’g’ri to’rtburchaklarni
toping. To’g’ri t o’rtburchaklar orasidan kvadratlarni ajtating. [1 4,11 -
mashq]
…
4
3
2
1](/data/documents/8f6d45a3-c2a8-4703-b91f-ce62dd3f391f/page_42.png)

![44
Masalan: har bir shaklni t o’g’ri t o’rtburchak va 2 ta uchburchakka ajrating. [1 5,
12 -mashq]
Figurani b o’laklarga b o’lishning xususiy holi bu figurani teng b o’laklarga
bo’lishdir. O ’quvchilar kesmalarni, k o’pburchaklarni teng qismlarnga b o’lishni
o’rganadilar .[II.20 .75]
Boshlang ’ich sinflar uchun Davlat ta ’lim standarti talabiga asosan boshlang ’ich
sinflarda o’quvchilar tevarak -atrofdagi geometrik shakllarni tanish, topa olish
ko’nikma va malakalarini egallashlari talab etiladi. Demak, o’quvchilar atrof -
muhitda geometrik figuralarni tanishga doir mashqlar bilan bir qatorda:
A) Murakkab geometrik figuralarda tanish figuralarni topishga doir
mashqlar bilan tanishadilar. Masalan, uchburc haklar nechta? Kvadratlar nechta?
To’g’ri t o’rtburchaklar nechta?. [ 27, 9 -mashq]
.
B) Umumiy elementga ega bulgan figuralarni izlashga doir mashqlar bilan
tanishadilar. Masalan,
1) VD kesma umumiy b o’lgan beshta shaklni ayting?
2) AE kesma qaysi shakllar uchun umumiy b o’ladi? [75, 7 -mashq]
Figurani chizing,
qirqib oling
Figurani chizing, qirqib
oling, bo ’laklarga bo ’ling.
Figurani chizing, qirqib
oling, bo ’laklarga bo ’ling,
yangi figura yasang.](/data/documents/8f6d45a3-c2a8-4703-b91f-ce62dd3f391f/page_44.png)
![45
A E
V) Murakkab geometrik figuralarda bir nechta figuraning umumiy qismidan
iborat b o’lgan figurani topishga doir mashqlar bilan tanishadilar. Masalan [ 87 ,5-
mashq]
.
Chapdagi rasmdan 5 ta uchburchak, o’ngdagi rasmdan 5 ta t o’rtburchak topib
tanishadilar.
Biz yuqorida o’quvchilarda burchak haqida dastlabki tasavvur xosil qilishda
uni «uchburchakning uzib olingan» burchagi sifatida talqin etilishi haqida aytib
o’tdik . Shuni aytish lozimki, boshlang ’ich sinf o’quvchilari burchaklar haqida biroz
cheklangan ma ’lumot oladilar: faqat t o’g’ri va t o’g’ri emas burchaklarni farqlashni
o’rganib, burchakning uchi va tomonlarini ajrata oladilar xolos. Bu bosqichda ular
burchakning tomonlari nurlardan iborat ekanligini anglab yetmaydilar. Qog ’oz
varagini buklash y o’li bilan o’quvchilar t o’g’ri burchak modelini xosil qiladilar,
ularni burchaklarga q o’yish usuli bilan berilgan burchaklar ichida t o’g’ri yoki t o’g’ri
emas burchaklarni ajratishni o’rganadilar.
V D](/data/documents/8f6d45a3-c2a8-4703-b91f-ce62dd3f391f/page_45.png)



![49
umuman har qanday figuraning yuzini (paletka yordamida) topish malakasini
egallab olishlari kerak.
Kichik maktab yoshidagi o’quvchilarga matematikani o’rgatish jarayonida hal
etiladigan k o’p masalalar ichida o’quvchilarning fazoviy tafakkur va tasavvurlarini
rivojlantirish kam ahamiyat kasb etmaydi (ya ’ni katta ahamiyatga ega ).[II. 21 .68]
Shu narsa aniqki avvalgi mavjud dastur va metodikaga qaraganda hozirgi
zamon boshlang ’ich maktabi juda ham ilgarilab ketgan. Boshlang ’ich sinflarda
matematikani o’rganish davomida geometrik material talab va imkoniyat darajasida
arifmetik material bilan bo g’langan.
Tekis figuralarning boshqa xossalari orasida yuzalarni o’lchash amaliy usulga
asoslangan. Dastur b o’yicha “Yuz. Yuz birliklari ” mavzusi IV sinflarda o’rganiladi.
Yuz haqida boshlang ’ich tushunchalarni shakllantirish b o’yicha tayyorgarlik ishi I -
II sinflardan boshlanadi.
Bosma asosidagi daftarlar bilan ishlashda figuralarni b o’yash, mehnat
darslarida qog ’ozdan figuralar qiyib olish, tasviriy san ’at darslarida rasm solish
figurani tekislikning yopiq chiziq bilan chegaralangan b o’lagi sifatida mexani k
qabul qilishiga imkon beradi.
Geometrik sanoq materialidan foydalanib, bolalar bir -biridan juda farq
qiladigan yoki mutlaqo bir xil b o’ladigan figuralarni bemalol taqqoslaydilar. Biroq
tajriba shuni k o’rsatadiki, bolalar “figuraning yuzi ” mavzusi materia lini qiyinchilik
bilan o’zlashtiradilar.Masalan, turli shakldagi narsalarni taqqoslash k o’pincha uning
chiziqli o’lchamla rini taqqoslashga keltiriladi.
Bolalar k o’pincha yuzni o’lchash tushunchasini uni ratsional hisoblash usuli
bilan aralashtirib yuboradi lar. ”To’g’ri t o’rtburchakning yuzini o’lchash nimadan
iborat? ”,- degan savolga bolalar k o’pincha bunday javob beradilar: ”bu uning
bo’yini va enini o’lchab, ularni k o’paytirish demakdir ”. Biroq t o’rtburchakning
yuzini topish degan s o’z unda yuz birligi (s m2, m2) necha marta joylashshini
aniqlashdir.
Mazkur mavzuni o’rganishda o’qituvchi tilga oid qiyinchilikka duch keladi,
chunki u geometriyadagi “tekislik ” tushunchasiga tayana olmaydi. Shu sababli yuz](/data/documents/8f6d45a3-c2a8-4703-b91f-ce62dd3f391f/page_49.png)





![56
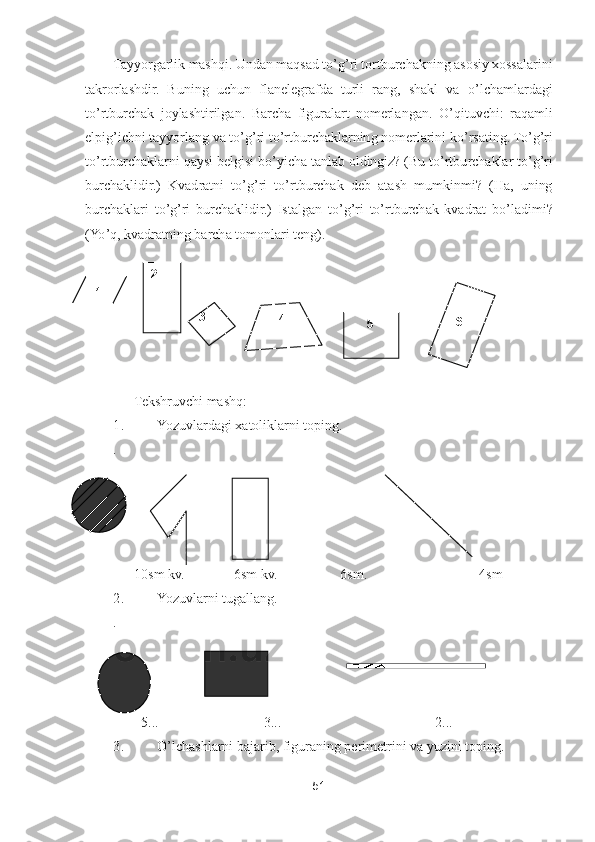
10. To’g’ri t o’rtburchakning: a) yuzi 1 m2, balandligi 5 dm ga teng. Asosini
toping; b) yuzi 30 dm2, asosi esa 6 dm ga teng. Perimetrini toping.
11. To’g’ri t o’rtbur chakning tomonlari uzunliklari 10 sm va 6 sm. Perimetri
sh u t o’g’ri t o’rtburchak perimetriga teng b o’lgan kvadratning yuzini toping.
12. Soat 6 da osma soat 6 marta bong urdi. Agar birinchi bongdan oltinchi
bonggacha 30 sekund o’tgan b o’lsa, soat 12 da 12 mar ta bong urishi uchun qancha
vaqt ketadi?
Boshlang ’ich sinflarda geometriya elementlarini o’rganishning asosiy (bosh)
maqsadlaridan biri o’quvchilarning fazoviy tasavvurlarini rivojlantirish b o’lib, bu
narsa (hayolda) qayta tiklangan obrazlarni (shakllarni) ajratib olishga va boshqatdan
ulardan kombinatsiya qilgan holda (tiklashga) yordam beradi. Biroq ajratib olishga
obrazlarni kayta kombinatsiyalashga (birlashtirish) faqat geometrik obrazlarni
ajratib olishnigina emas, balki ular orasidagi turli -tuman muno sabatlarni ham
bilishni takozo etadi (k o’zda tutadi), chunki yangi figuralar hosil qilish ular
elementlari orallarida ba ’zi munosabatlar t o’plamining mavjud b o’lishini nazarda
tutadi.
Uchinchi o’quv yilining ohirida qachonki bolalar ma ’lum darajada geometr ik
tasavvurlar majmuasiga ega b o’lgach ma ’lum umumlashtirishlarga ehtiyoj tug ’iladi,
o’quvchilar figuralarning ta ’riflariga yaqinlashgan tavsiflarini bera olishlari kerak.
Tabiiyki, tushunchalarni hosil etish jarayonida umumlashtirishlar muhim
ahamiyat kasb etadi. Biroq geometrik tushunchalarini hosil etish jarayonida
umumlashtirishlar qilishda fazoviy munosabatlar ham katta ahamiyatga ega.
O ’rganilgan fazoviy munosabatlarni bir holatdan boshqasiga o’tkazish darajasi
umumlashtirishlar darajasini xarakterlaydi .[II.20 .101]
Ha, albatta, o’quvchilar tanishadigan geometrik tushunchalar mazmuni
obrazlar tushunchalari ma ’lum munosabatlar sistemasi bilan xarakterlanadi.
Tushunchalarn i hosil qilish, shakllantirish va rivojlantirishda turli tuman
elementlar va ob ’ektlar t o’plamlari orasida izomor fizmni o’rnatar ekanmiz biz
nafaqat bu ob ’ektlar orasida, balki asosiy munosabatlar orasida ham ikki tomonlama
moslik o’rnatamiz, chunki bu ob ’ektlar turli tabiatga ega. Tabiiyki, boshlang ’ich](/data/documents/8f6d45a3-c2a8-4703-b91f-ce62dd3f391f/page_56.png)











1 BOSHLANG ’ICH SINF O ’QUVCHILARIGA ENG SODDA GEOMETRIK SHAKLLARNI O ’RGATISHDA ZAMONAVIY TEXNOLOGIYALARNI QO ’LLASH MUNDARIJA KIRISH .............................................................................. ... ................ .... ......3 I BOB BOSHLANG ’ICH SINFLARDA GEOMETRIYA ELEMENTLARINI O ’QITISHNING NAZARIY ASOSLARI 1.1Geometriya fani va uning rivojlanish tarixi haqida .... ................... .............7 1.2Boshlang ’ich sinflar matematika kursida (1 -4-sinflar)da o’rganiladigan geometrik materialning mazmuni ..................................... ..................... ........ .........12 1.3 Boshlang ’ich sinflarda geometrik ma terialni o’rgatishning umumiy masalalari .............................................................................. ...................................27 II BOB BOSHLANG ’ICH SINFLARDA GEOMETRIYA ELEMENTLARINI O ’RGATISHNING METODIKASI 2.1 Boshlang ’ich sinf o’quvchilarida uzunlik haqida tasavvurlarini shakllantirish, uzunliklarni o’lchash malakalarini hosil qilish ............ ............. ......... ............ ....... ...................................................................36 2.2 Geo metriya elementlarini o’qitishda k o’rgazma qurollaridan foydalanishning afzalliklari ............................................................ ....... .................................... ........50 III BOB O ’TKAZILGAN TAJRIBA - SINOV ISHLARI, NATIJALARI TAHLILI .......... ................... ..................................................................... ......... ...60 XULOSA .................................................................................. .................. ...66 FOYDALANILGAN ADABIYOTLAR ............. ....................................... .69
2 KIRISH O ’zbekiston Respublikasi Vazirlar Mahkamasi tomonidan tasdiqlangan “Davlat ta ’lim standarti t o’g’risidagi Nizom ”ga binoan umumiy o’rta ta ’lim, shu jumladan, boshlang ’ich ta ’lim bosqichi uchun ham alohida -alohida davlat ta ’lim standarti talablari va me ’yoriy k o’rsatkichlari belgilab q o’yadi. “Ta ’lim t o’g’risida ”gi Qonunda ta ’kidlanganidek: “Maktabning birinchi sinfiga bolalar olti -yetti yoshdan qabul qilinadi. “Boshlang ’ich ta ’lim konsepsiyasi ”da e’tirof etilganidek, olti yoshga t o’lgan har qanday bola aqliy, ruhiy hamda jisminiy jihatdan maktabda o’qish uchun tayyor b o’lganida, maktabning moddiy -texnik bazasi bunday bolalarga ta ’lim berish uchun yetarli deb hisoblanganda ha mda o’qituvchilar pedagogik va psixologik jihatdan olti yoshli bolalarni o’qitishga qodir deb topilganda maktabga qa bul qilinadilar. Prezidentimiz SH.M.Mirziyoyev ta ’kidla ganidek: “Boshlang ’ich ta ’lim o’qish, yozish, sanash, o’quv faoliyatining asosiy malaka va k o’nikmalari, ijodiy fikrlash, o’zini -o’zi nazorat qilish uquvi, nutq va xulq -atvor madaniyati, shaxsiy gigiyena va sog ’lom turmush tarzi asoslarining egallab olishini ta ’minlashga da ’vat etilgan. Shunday ekan, ushbu asosda boshlang ’ich sinflarda o’quvchilarning umum madaniy va axloqiy k o’nikmalari, dastlabki savodxonlik malakalari shakllantirilishi lozim ”.[I.6 .56] Boshlang ’ich ta ’lim jarayoni bolalarning mantiqiy tafakkur qila olish salohiyati, aqliy rivojlanishi, duyoqarashi, kommunikativ savodx onligi va o’z- o’zini anglash salohiyatini shakllantirishga, jismonan sog ’lom b o’lishga, moddiy borliq g o’zalliklarini his eta olishga, g o’zallik va nafosatdan zavqlana olish, milliy urf -odatlarni o’ziga singdirish va ardoqlash, ularga rioya qilishga o’rga tadi.Boshlang ’ich ta ’lim bosqichi oldiga qo’yilgan vazifalarning bajarilishini nazorat qilish orqali amalga oshiriladi. Ta ’lim standarti asosida boshlang ’ich sinf o’quvchilaridan standartda belgilab q o’yilgan ko’rsatkichga erishishni talab qiladi va o’z na vbatida, bu k o’rsatkichlarga erishish uchun zarur b o’lgan ta ’limiy xizmatlar va vositalar bilan ta ’minlaydi. Boshlang ’ich
3 ta ’lim bosqichiga davlat va jamiyat tomonidan q o’yilgan talabda ta ’lim sohalari bo’yicha o’zaro muvofiqlik, mutanosiblik, uyg ’unlik t o’la ta ’minlangan b o’lmog ’i kerak. O ’zbekiston Respublikasining jahon hamjamiyatiga integratsiya ta ’lim sohasida nafaqat yangi imkoniyatlarni ochdi,balki o’quvchi yoshlarga ta ’lim va tarbiya berishda yuqori sifatga erishishni ta ’minlashni taqazo etdi. Bu n atijalarga erishish uchun o’z vaqtida O ’zbekiston Respublikasining “Ta ’lim t o’g’risida ”gi Qonuni hamda “Kadrlar tayyorlash milliy dasturi ”qabul qilingandir. ”Ta ’lim to’g’risidagi qonunning 7 -moddasida belgilab berilganidek, “Davlat ta ’lim standartlari umumi y o’rta, o’rta maxsus, kasb -hunar va oliy ta ’lim mazmuniga hamda sifatiga q o’yiladigan talablarni belgilaydi. O ’zbekiston Respublikasining birinchi prezidenti I.A.Karimov “Ta ’lim -tarbiyava kadrlar tayyorlash tizimini isloh qilish,barkamol avlodni voyaga ye tkazish t o’g’risida ”gi Qonuni va “Kadrlar tayyorlash milliy dastur ”da matematika o’qitishning sifatini oshirish bilan birga o’quvchilarning tafakkuri va shaxsiy sifatlarini,matematik savodxonligini shakllantirish hamda ijodiy qobilyatlarini o’stirish masal alari belgilab berilgan.Dastur matematik tushunchalarning hayotiy materiallar asosida o’zlashtirish lozim b o’lgan tushuncha va qoidalar amaliyotga xizmat qilishini, hayotiy materiallar asosida o’quvchilarga yetkazib berish imkonini beradi. Shu bilan bir qa torda, fan va amaliyot o’rtasidagi aloqalarni t o’g’ri tushunishga asos yaratadi. O ’rta maktab ta ’lim tizimini isloh qilish jadal sur ’atlar bilan olib borilayotgan hozirgi davrda maktab matematikasini mazmuni jihatdan k o’rib chiqish zarur talabi bo’lib, o’qu vchilarning bilim va malakalarini jahon talablari doirasida b o’lishi talab qilinadi.Buning uchun esa boshlang ’ich sinfdanoq har tomonlama yetuk insonlar tayyorlashga harakatni boshlash lozim. Bunda esa dars jarayonlarida zamonaviy kompyuter texnologiyalari dan foydalanish zarurdir. Boshlang ’ich sinf uchun darslik va o’quv q o’llanmalari ( K.Qosimova, R.A.Mavlonova, L.SH.Levenberg), o’qituvchilar uchun q o’llanmalar (M.I.Mopo, A.M.Pishkalo, L.SH.Levenberg, N.U.Bikbayeva) va o’quvchilar uchun tajriba sinov mater iallari (M.Ahmedova, N.Abdurahmonova, R.Ibragimov, Y.M.Kolyagin, P.M.Erdniyev) orqali boshlang ’ich maktab o’quvchilarining bilish faoliyatini
4 shakllantirish mumkinligiga t o’xtalib o’tilgan. Ta ’lim metodikasiga bag ’ishlangan ishlarda (P.M.Erdniyev,N.U.Bikba yeva, L.SH.Levenberg, R.A.Mavlonova, K.Qosimova va boshqalar) geometriya elementlarini o’qitish muammosi umumiy holatda k o’zda tutiladi, biroq maxsus tadqiqot predmeti sifatida ajratib olinmagan. O ’quvchilarning geometrik tasavvurlarini tizimli shakllantir ish hamda egallangan bilimlarni amaliy faoliyatda q o’llay olishga o’rgatish boshlang ’ich ta ’limning muhim vazifalaridan biridir. Bitiruv malakaviy ishining dolzarbligi ham aynan shunda, shu masalalarga biroz b o’lsada oydinlik kiritishdadir, ya ’ni o’quvchilarga geometriya elementlarini o’qitishning yangi shakl va metodlarini ta ’lim jarayoniga olib kirish boshlang ’ich sinflarda matematika o’qitishni bir oz bo’lsa ham yengillshtirishtiradimi? Bolalarni maktabda boshlang ’ich sinfdan keyingi sinflarga o’tishda vujudga keladigan qiyinchiliklarni bartaraf etadimi? Shu jihatdan boshlang ’ich talim standartini belgilash ta ’lim jarayoning tarkibini xuddi shu tarkib komponentlarining mazmunini modernizatsiyalash, boshlang ’ich ta ’lim jarayonida yangi, zamonaviy p edagogik texnologiyani q o’llash imkonini berad . Boshlang ’ich sinf o’quvchilariga matematikadan samarali ta ’lim berilishi uchun b o’lajak o’qituvchi boshlang ’ich sinflar uchun ishlab chiqilgan matematika o’qitish metodikasini egallab, chuqur o’zlashtirib olm og ’i zarur. Bitiruv malakaviy ishining dolzarbligi – kichik yoshdagi o’quvchilarni geometrik tushunchalarini boyitish, geometrik terminlar b o’yicha nutqlarini o’stirish va matematika darslarida didaktik tamoyillar yordamida geometriyaga oid misol va masala lar yechish b o’yicha bilim va malakalarni oshirish. Hozirgi zamon matematikasi natural son tushunchasini asoslashda t o’plamlar nazariyasiga tayanadi. Chekli t o’plamlar elementlari orasida o’zaro bir qiymatli moslik o’rnatish o’zaro ekvivalent t o’plamlar si nflarini ajratish imkonini beradi, shu bilan birga bu sinflarning har birini xarakterlovchi umumiy narsa -natural sonlarni ajratish imkonini beradi. Geometrik material boshlang ’ich sinflar uchun mustaqil bo’lim sifatida o’quv dasturiga kiritilmaydi. O ’quv j arayonida geometriya elementlarini o’rganish bilan bevosita bog ’lab olib boriladi.
5 Geometrik mazmundagi masalalarni yechish, hisob -kitobga o’rgatish davomida geometrik figuralardan, didaktik material sifatida foydalanish – bularning barchasi o’quvchilarnin g geometrik taasurotlarini mustahkamlashga imkon beradi. Bitiruv malakaviy ishining maqsadi – boshlang ‘ich sinf o’quvchilarini geometrik tushunchalar bilan tanishtirish va geometrik masalalarni yechishga o’rgatishda didaktik tamoyillardan foydalanishni ama lga oshirish usullari ishlab chiqishdir. Bu mavzuni yoritish jarayonida o’z oldimizga quyidagi vazifalarni qo’ydik: • Boshlang ’ich sinf o’quvchilarini geometrik tushunchalar bilan tanishtirishning ahamiyatini nazariy hamda amaliy asoslash: • Boshlang ’ich sinf o’quvchilarini geometrik materialga oid masalalar yechishga o’rgatishda didaktik materiallardan foydalanish usullarini ishlab chiqish; • Boshlang ’ich sinf o’quvchilarini geometrik materialga doir misollarni yechishga va tekshirishga o’rgatishda k o’rsatmali v ositalardan foydalanishning ahamiyatini yoritib berish. Bitiruv malakaviy ishining obyekti 1–4 sinf matematika kursida geometrik materillarni o’rganishni samarali amalga oshirishni takomillashtirish jarayonidan iborat. Bitiruv malakaviy ishining predmeti: 1–4 sinf matematika darslarida o‘quvchilarning geometriya elementlari va u bilan bog ‘liq tushunchalar haqidagi tasavvurlar shakllanishiga olib keluvchi hamda yasashga oid geometrik mazmundagi masalalarni yechishni amalga oshirish usullarini ishlab chiqis h1. Bitiruv malakaviy ishining metodologik asosi: “Ta ’lim to ‘g‘risida ”gi O ‘zbekiston Respublikasi Qonuni, O ’zbekiston Respublikasi Konstitutsiyasi “Kadrlar tayyorlash milliy dasturi ”, O ’zbekiston Respublikasi Birinchi Prezidenti I.A.Karimovning intellektual salohiyatni yuksaltirishga doir g’oyalari, O ’zbekiston Respublikasi Prezidenti SH.M.Mirziyoyev tomonidan qabul qilingan qaror va y o’l-yo’riqlar, “O ’zbekiston Respublikasini yanada rivojlantirish
