To’g’ri chiziqli sterjenning bo’ylama tebranishi









O’ZBEKISTON RESPUBLIKASI OLIY VA O’RTA MAXSUS TA’LIM VAZIRLIGI SHAROF RASHIDOV NOMIDAGI SAMARQAND DAVLAT UNIVERSITETI MATEMATIKA FAKULTETI NAZARIY VA AMALIY MEXANIKA kafedrasi Elastik tebranishlar nazariyasi fanidan MUSTAQIL ISH Mavzu: To’g’ri chiziqli sterjenning bo’ylama tebranishi Bajardi:____-guruh talabasi _________________ ____________________ _ Qabul qildi: _______________________ Mustaqil ish topshirilgan vaqt _________ Mustaqil ish qabul qilingan vaqt_________
Samarqand 2022
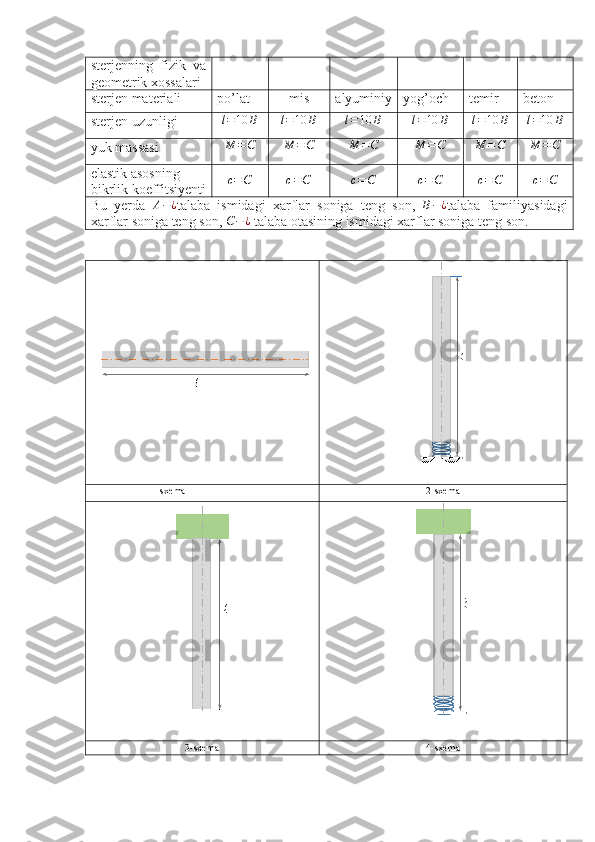
Mustaqil ishni bajarish tartibi: Xar bir talaba avval namunaviy yechib ko’rsatilgan masalalar bilan tanishib chiqadi so’ngra o’zining jurnaldagi nomeri bo’yicha o’ziga tegishli bo’lgan masalaning qiymatlarini oladi. Mustaqil ishni bajarayotgan vaqti avval mavzuga tegishli asosiy tushunchalarni yozib so’ngra masala yechiladi. Namunaviy masalalarni yozish shart emas. Xar bir talaba chizmalarni chizishda koordinata o’qlarini kiritishga, kuchlarning yo’nalishini qo’yishga alohida e’tibor berishi, mustaqil ish yuzi namunadagidek bo’lishi va mustaqil ish oxirida foydalanilgan adabiyotlar ro’yxati keltirilishi talab etiladi. To’g’ri chiziqli sterjenning bo’ylama tebranishi To’g’ri chiziqli sterjenning bo’ylama tebranish harakatini tekshirganimizda, tekis kesim gipotezasidan foydalanib sterjen kesimidagi zarralarning ko’ndalang yuza bo’yicha bajaradigan harakatini hisobga olmay, faqat sterjen o’qi bo’yicha bajariladigan harakatnigina ko’zda tutamiz. Sterjendan uning ikkita ko’ndalang kesimi vositasi bilan bir element ajratamiz (1-rasm), bu ajratilgan elementga Dalamber prinsipini tatbiq qilib, quyidagi differensial tenglamani olamiz: − N +( N + ∂ N ∂ x dx ) = ρSdx ∂ 2 u ∂ t 2 . ∂N ∂x dx = ρSdx ∂2u ∂t2. yoki ∂ N ∂ x = ρS ∂ 2 u ∂ t 2 . ( 1) bu yerda ρ − ¿ sterjen materiali zichligi, S − ¿ sterjen ko’ndalang kesim yuzasi, N −¿ kesimdagi bo’ylama kuch, u − ¿ tekshirilayotgan kesimning x o’qi bo’yicha ko’chishi. Ajratilgan elementning chap kesimi x o’qi bo’yicha u ga ko’chsa, o’ng kesimi esa u+∂u ∂xdx ga ko’chadi. Elementning asolyut cho’zilishi ∂u ∂xdx , nisbiy cho’zilishi esa ε= ∂u ∂x bo’ladi. Kesimdagi bo’ylama kuch Guk qonuniga muvofiq quyidagicha bo’ladi:
N = ESε = ES ∂u ∂x. N ning qiymatini (1) ga qoysak: E ∂ ∂ x ( S ∂ u ∂ x ) = ρS ∂ 2 u ∂ t 2 yoki 1 S ∂ ∂x(S∂u ∂x)= 1 a2 ∂2u ∂t2(2) kelib chiqadi. Bunda: a 2 = E ρ ( 3 ) bo’ladi. Bu yerda a−¿ bo’ylama to’lqinning tarqalish tezligi. Sterjenning ko’ndalang kesim yuzi o’zgarmasa tenglama yana ham osonlashadi: a 2 ∂ 2 u ∂ x 2 = ∂ 2 u ∂ t 2 ; ( 4 ) Bo’ylama tebranma harakatni ifodalovchi funksiya u ( x , t ) kesimning holatini aniqlovchi x va t ga bog’liqdir. Shuning uchun bu u ( x , t ) funksiyani ikki funksiyaning ko’paytmasi tarzida ifodalaymiz: u(x,t)= X (x)T(t);(5) Bu funksiyalarning har qaysisi bitta o’zgaruvchiga bog’liqdir. u ( x , t ) ning bu qiymatini (4) ga qo’yib, quyidagi munosabatni hosil qilamiz: a2X''T= X ¨T Shtrix bilan x ga nisbatan, nuqta bilan t ga nisbatan hosila olingan. Chiqqan munosabatni quyidagicha yozamiz: a 2 X ' ' X = ¨ T T Bu munosabatning chap tomoni faqat x ning, o’ng tomoni esa faqat t ning funksiyasidir. Munosabat x va t ning har bir qiymatida mavjud bo’lishi uchun, uning har qaysi qismi bitta o’zgarmas songa teng bo’lishi kerak. Biz bu o’zgarmas sonni − p2 orqali belgilaymiz, u holda yuqoridagi munosabatdan ikkita, bir-biridan mustasno, differensial tenglamalarni olamiz: a 2 X ' ' X = − p 2 , ¨ T T = − p 2 ; bulardan: ¨ T + p 2 T = 0 , X ' ' + p 2 a 2 X = 0 } ( 5 1 ) kelib chiqadi. Bu tenglamalarning har ikkalasining ham integrali bizga ma’lum ular quyidagicha bo’ladi:
T( t) = C 1 cospt + C 2 sinpt ( 6 ) yoki T(t)= Asin (pt +φ) X (x)=C3cos p a x+C4sin p a x(7) (6) tenglama harakatning tebranma xarakterligini ko’rsatadi; p esa bu tebranma harakatning takrorligidir. Tebranma harakat jarayonida vaqtga qandaydir bir muayyan qiymat berilsa, masalan, t=t1 bo’lsa u holda T1(t1) o’zgarmas songa aylanadi. Bu vaqtda u(x,t)=T1X (x) bo’ladi, ya’ni u ( t 1 , x ) faqat x ning funksiyasiga aylanadi. Bundan ko’ramizki, X ( x ) funksiya kesimlarning ko’chish formulasini aniqlar ekan. Biror kesimning holati oldindan belgilab qo’yilsa, masalan x = x 1 bo’lsa, har bir onda kesimning formasi o’zgarmay, mazkur kesim boshqa kesimlar kabi (6) ga muvoviq tebranma harakatni bajaradi. Tebranma harakatning takrorligi p ni aniqlashdan oldin, uning soni cheksizligini ta’kidlab o’tamiz. p n ning har bir qiymatiga muvofiq Tn(t) funksiya va tebranish formasi maxsus forma Xn(x) ga mos keladi. Shuning uchun (5) ko’rinishda olingan yechim tenglamaning xususiy integralidir. Harakat tenglama (4) ning to’la integrali barcha xususiy integrallarning yig’indisidan iborat bo’ladi: u ( x , t ) = ∑ n = 1N X n ( x ) T n ( t ) ( 8 ) Bunda X n ( x ) tebranishning xususiy funksiyasi yoki fundamental funksiya deb ataladi. Ko’pincha bu funksiya faqat tebranishning normal formasi deb ham yuritiladi. Endi takrorlik (chastota) p ni aniqlash tenglamasini tuzishga o’tamiz. Buning uchun masalaning chagaraviy shartlaridan foydalanamiz. Quyida chegaraviy shartlar bilan tanishamiz: 1) Sterjenning bir uchi qistirib qo’yilgan bo’lsin (1-rasm). Sterjenning qistirilgan uchida har bir vaqt uchun u = 0 bo’ladi. Shunga ko’ra: X ( 0 ) = 0 bo’lishi kerak. 2) Sterjenning uchi erkin bo’lsin. U holda sterjenning erkin uchida bo’ylama kuch N =0 bo’lishi kerak. Guk qonuniga muvofiq N = ESε = ES ∂ u ∂ x = EST X ' = 0 bundan X'(l)=0 bo’ladi.
