YORIQ-G’OVAK MUHITLARDA ANOMAL MODDA KO’CHISHI TESKARI MASALASINI SONLI YECHISH









![o'lchovlar bilan aniqlanadi. Parabolik tenglama (1.1 ) uchun xuddi shunday
teskari masalani misol qilib keltiramiz .
Biz o'lchovlar oraliqning [0,l] o'ng uchida mavjud emas deb taxmin
qilamiz, lekin ichki
x¿ nuqtadagi yechim ma'lum, ya'ni (1.2) o'rniga, quyidagi
shartlar berilgan.
u(0,t)= 0, u(x¿,t)= ϕ(t), 0<t≤ T .
( 1.7)
chegarani o'lchash imkoni bo'lmagan qismidagi oqimni
x= l ni aniqlashdan
iborat (ko'rib chiqilayotgan misolda ) . Bu (1.1), (1.3), (1.7) shartlaridan
funksiyalarni topishga mos keladi
{u(x,t),k(l)∂u
∂x
(l,t)} .
Evolyutsion teskari masalalar. Matematik fizikaning statsionar
bo'lmagan masalalari uchun to’g’ri masala boshlang'ich shartlarni belgilash
bilan tavsiflanadi (masalan (1.3) ga qarang). Evolyutsion teskari masalalar
haqida biz boshlang'ich shartlar aniqlangan teskari masalalarni tasniflaymiz
(ular masalani to’g’ri shakllantirish uchun yetishmaydi).
Ko'rib chiqilayotgan (1.1)-(1.3) to’g’ri masalaga nisbatan eng oddiy
evolyutsion teskari masala quyidagicha tuzilgan . Bizga (1.3) dastlabki shartlar
berilmagan, lekin biz oxirgi vaziyatda yechimni bilamiz
t= T :
u(x,T )= uT(x), 0≤ x≤ l.
(1.8)
tenglamani yechimini o’tgan vaqt momentida topishdir.
Bir jinslimas g’ovak muhitda modda ko’chishda teskari masalalar
Matematika fizika bo'yicha kurslarda differensial tenglamalar qismi uchun
to’g’ri chegaraviy masalalarni shakllantirish odatiy holdir. Ikkinchi tartibli
elliptik tenglamalar uchun chegaraviy yechimning qo shimcha shartlari
ʻ
(birinchi, ikkinchi yoki uchinchi turdagi) berilgan. Masala va uning natijasi
10](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_10.png)


![Darsi qonunini ifodalovchi tenglamalardan tashkil topgan [100] asosida
ishlab chiqilgan chuqur qatlamli filtratsiya modeliga asoslangan [120]. Bu
kvazichiziqli tenglamalar tizimi ikkita empirik koeffitsientga ega bo'lib,
g'ovak muhitdagi qatlam shikastlanishini ifodalovchi o'tkazuvchanlikni
pasaytirish funksiyasi k ( σ )
va zarrachalarni ushlab turish kinetikasini
ifodalovchi λ ( σ )
filtratsiya funksiyasi mavjud. To'g'ri masala bu
tenglamalar tizimini vaqt ichida hal qilishdan iborat.
Bir o'lchovli oqim laboratoriya tajribalarida qiyinchilik ortib
borayotgan tartibda quyidagi miqdorlarni aniq o'lchash mumkin:
(1) vaqt seriyasida ∆ p( T )
bosimning pasayishi;
(2) tog' jinsi bo'ylab ba'zi nuqtalarda
X= Xl,l=1,… n, pl(T) bosim vaqt
seriyasi;
(3)
ce(T) vaqt qatori oqava suv konsentratsiyasi;
(4) eksperimentning yakuniy vaqtida
Xl−1 va X
l l = 1 , … n
nuqtalari
orasidagi σ ( X , T )
o'rtacha zarracha cho'kishi;
(5) zarrachalarning σ ( X , T )
ko p
ʻ (Xl,T j),l=1,… ,nj=1,… ,m nuqtalarda
cho kishi.
ʻ
Tabiiyki, bunday eksperimental o'lchovlar o'tkazuvchanlikni
kamaytirish
k(σ) va λ ( σ )
filtratsiya funktsiyasini aniqlashning teskari
masalasi qo'llaniladi. O'tkazuvchanlikni pasaytirish va filtratsiya
funktsiyalarini tiklash Alvarez ishining ob'ekti bo'lgan bir nechta turli xil
noto'g'ri teskari masalalarga olib keladi. Bu yerda qo'llaniladigan yechim
usullari diskretizatsiya qilinganda katta matritsalarga olib keladi, ular juda
katta holat sonlarga ega va ehtiyotkorlik bilan amalga kerak.
Oqim suv konsentratsiyasi tarixidan
ce(T) doimiy filtratsiya funksiyasi
λ ( σ )
ni aniqlash usullari [93] va [96] da keltirilgan. Zarrachalarning
yuborilgan kontsentratsiyasi o'zgarmas degan faraz ostidagi umumiy
13](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_13.png)
![holatni tiklash usulida funktsional tenglamaga asoslangan holda taqdim
etilgan. Xususiyatlar chiziqlari bo'yicha c / σ
ning o'zgarmasligiga
asoslangan ushbu funktsional tenglamaning birinchi hosila topilgan. Biroq,
teskari usulning barqarorlashuv shartlari, shuningdek, modelning
eksperimental tasdiqlanishi hisobga olinmadi. Ushbu ishda biz qayta
tiklash usuli uchun stabilizatsiya shartlarini olamiz va doimiy in’ektsiya
qilingan zarracha konsentratsiyasi taxminni bo'shatamiz. Bundan tashqari,
optimallashtirish usuliga asoslangan filtratsiya funktsiyasi λ ( σ )
ni olish
uchun yana bir tiklash usulini taqdim etamiz.
Xarakteristikalar chizig'i bo'ylab c / σ
ning o'zgarmasligi birinchi bo'lib
Herzig va boshqalar tomonidan topilgan. Filtrlash jarayonining
soddalashtirilgan modeliga asoslangan. Biroq, xuddi shu munosabat
o'xshash taxminlar ostida Bedrikovetsky va boshqalar tomonidan
umumiyroq model uchun olingan. Qayta tiklash usuli va modelni qo’llash
uchun uning dolzarbligi sababli, Alvarez shunga o'xshash hosilani
takrorlagan. O'tkazuvchanlikni pasaytirish funktsiyasi k ( σ )
ni bosim
tushishi tarixidan ∆ p(T) aniqlash usullari doimiy koeffitsient va
moddalarning bir parametrli oilasi uchun [109], [98] keltirib o’tgan. U bu
ishida Tixonov regulzatsiya usuli yordamida umumiyroq usulni olgan.
Bundan tashqari, ikkita parametr funksiyasi uchun ishlab chiqilganga
o'xshash parametrlash usuli bilan tartibga solishni taqdim etgan.
[72] da ikkita masalani hal qilgan: filtratsiya funksiyasi λ ( σ )
uchun
∆ p
( T )
va c ( X , T )
zarrachalar konsentratsiyasini hisoblashning bevosita
masalasi,shuningdek, zarrachalarning in'ektsion konsentratsiyasini doimiy
deb hisoblab, oqava suv konsentratsiyasi
ce(T) filtratsiya funksiyasini λ ( σ )
aniqlashning teskari masalasi.
Alvarez bu ishda quyidagi teskari masalalarni yechgan. Birinchidan,
g'ovak muhitlarning shikastlanishi funksiyasi
k(σ) bir o'lchovli chuqur
qatlamli filtratsiya oqimida bosim tushishi tarixidan ∆ p
( T )
tiklanadi. Bu
14](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_14.png)

![Filtratsiya funksiyasi λ( σ )
allaqachon topilgan deb faraz qilinib,
berilgan bosim tushishi tarixidan k
( σ )
o‘tkazuvchanlikni pasaytirish
funksiyasini aniqlashning teskari masalasini o‘rgangan. Bunda tog'
jinslarining hosil bo'lishining shikastlanish funksiyasi k
( σ )
uchun Volterra
tipidagi integral tenglamani olgan va operator tenglamasining yaxshi
joylashishi shartlarini muhokama qilgan. O'xshash integral tenglama [120]
da olingan. Bunda o'tkazuvchanlikni pasaytirish funksiyasi
k(σ) ni mos
yechimlar to'plamida hisoblash uchun sonli hisoblashni amalga oshirishni
tasvirlagan.
Klassik Tixonov yoki Tixonov-Filips tartibga solish birinchi turdagi
noto'g'ri qo'yilgan Volterra tenglamasini yaxshi qo'yilgan masalaga
qisqartirish uchun ishlatilgan ([94] va [106]). Optimallashtirish va LU
faktorizatsiya usullari uzluksiz tenglamani diskretlash orqali olingan
chiziqli tenglamalar tizimining yechish. Nihoyat, mumkin bo'lgan yechim
yuqori tartibli Sobolev normasiga nisbatan bir xilda chegaralangan deb
faraz qilgan holda, muntazamlashtirilgan yechimning yaqinlashuvi olinadi;
bu silliqlik xossasi. Buning uchun, integral operator tenglamaning
iteratlari deyarli minimal normaga ega bo‘lgan taxminiy yechimga
yaqinlashishi uchun yetarli shartdan foydalangan.
Konvergentsiya natijasi Hilbert shkalasi yordamida olinadi, bu
Tixonovni tartibga solish xatolarini o'lchash uchun foydali chegaralarni
beradi. Bundan tashqari, moddaning qovushqoqlik darajasini va silliqligini
tavsiflash uchun mukammal vositadir ([95], [101]).
G'ovak tog' jinslarining shikastlanishi
k(σ) va filtratsiya funktsiyasi
λ
( σ )
oqava suv konsentratsiyasi va bosimning pasayishi tarixini hisoblash
uchun optimallashtirish usuli keltirilgan. Bundan tashqari, oqava suv
zarralari kontsentratsiyasi tarixidan filtratsiya funktsiyasini olish uchun
optimallashtirish usuli ham tasvirlangan. Har bir teskari masalaning yaxshi
qo'yilganligi ham o'rganiladi.
16](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_16.png)
![Ikkala holatda ham tiklash jarayoni Martinez va boshqalar tomonidan
ishlab chiqilgan va amalga oshirilgan quti cheklovlari bilan proyeksiya
gradienti usuli yordamida chiziqli bo'lmagan funksionallikni
minimallashtirishdan iborat. ([114], [101], [108]). Funksional
eksperimental ma lumotlar va model tomonidan bashorat qilingan tegishliʼ
miqdorlar o rtasidagi farqni hisobga olgan holda eng kichik kvadrat
ʻ
formulasidan olinadi. Ushbu funksiyani baholash to g ridan-to g ri masala
ʻ ʻ ʻ ʻ
uchun aniq va barqaror raqamli usulni qo llashni talab qiladi.
ʻ Qutidagi
cheklovlar eritmaning pozitivlik va monotonlik kabi xususiyatlaridan kelib
chiqqan holda aniqlanadi, biz oqava suv konsentratsiyasi tarixidan λ
( σ )
filtratsiya funktsiyasini qayta tiklash usullarining to'g'riligini, shuningdek,
qayta tiklanishning yaxshi holatini aniqlaymiz. bosim tushishi tarixidan
o'tkazuvchanlikni pasaytirish funksiyasi k
( σ )
. Nihoyat, ikkala funktsiyani
bir vaqtning o'zida tiklash usuli ishlab chiqiladi.
U ma'lum bir chiziqli bo'lmagan operator tenglamalarini o'rgangan.
Chiziqli vaziyatdan farqli o'laroq, nochiziqli muammoli masalaning
umumiy nazariyasi mavjud emas. Biroq, bu yerda o'rganilgan chiziqli
bo'lmagan operatorlar uchun konvergentsiya va barqarorlikning ba'zi
natijalari mavjud, chunki bu operatorlar tegishli domenlarda ixchamlik va
zaif yopiqlik kabi yoqimli xususiyatlarga ega.
σ ( X , T )
zarrachalar yotqizishning tarqalish tarixidan filtratsiya
funksiyasi λ
( σ )
ni tiklash usullari taklif qilingan. Qayta tiklashning bir
nechta protseduralari mavjud: birinchisi chuqur qatlamli filtratsiya modeli
tenglamalarini to'g'ri shakllantirishdan foydalanadi. Zarrachalarni
cho'ktirish vaqtidagi farqlanish bu holda asosiy sonli qiyinchilikni keltirib
chiqaradi. Ikkinchi protsedurada filtratsiya funksiyasi λ
( σ )
birinchi turdagi
Volterra integral tenglamasining xarakteristik chiziqlar orqali yechimi
sifatida hisoblanadi. Keltirilgan usul ushbu tenglama uchun ham foydali
ekanligini ko'rishimiz mumkin. Uchinchi protsedurada filtratsiya
17](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_17.png)
![funktsiyasi λ( σ )
funktsional tenglama yordamida olinadi. To'rtinchi
protsedurada optimallashtirish usuli λ
( σ )
filtratsiya funktsiyasini
metodologiya bilan tiklaydi.
Barcha teskari masalalarda, empirik funktsiya parametrlarini
tiklashdan oldin, ushbu parametrlarni aniqlash mumkin bo'lgan shartlarni
bilish kerak, kuzatuv ma'lumotlari teskari yechimni aniqlash uchun
yetarlimi yoki teskari yechim kuzatuv xatolariga qanchalik sezgir. Shu
tarzda biz filtratsiya va o'tkazuvchanlikni kamaytirish funktsiyalarini
aniqlash uchun eng yaxshi eksperimental dizaynni aniqlagan.
Bu yerda ishlab chiqilgan usullardan eksperimental ma'lumotlardan
foydalangan holda chuqur qatlamli filtratsiya modelini laboratoriya
o'lchovlari bilan taqqoslash amalga oshirgan.
1.2. Yoriq-g'ovak muhitda anomal modda ko’chishining matematik
modellari
G'ovakli muhitlarda moddalarning ko’chishini matematik modellashtirish
tahlil qilish uchun samarali vositadir. Laboratoriya sharoitida eksperimental
tadqiqotlar yoki to'liq miqyosda, real sharoitlarda real tadqiqotlar bilan
solishtirganda, matematik modellashtirish turli parametrlarning xarakteristikalar,
o'tkazish ko'rsatkichlariga ta'sirini fizik jihatdan to'g'ri tasvirlash va miqdoriy
aniqlash imkonini beradi.
Suyuqlikda muallaq zarrachalarni ko’chishining klassik modellari
konvektiv ko’chish va zarrachalarning cho'kish kinetikasini hisobga oladi,
gidrodinamik dispersiya e'tiborga olinmaydi [58]. Ba'zi o'zgartirishlar va turli
omillarni qo'shimcha hisobga olgan holda bir qator shunga o'xshash modellar
[32,60] da taklif qilingan. Chiziqli holatda kinetik tenglama bilan birga moddani
ko’chish tenglamalari analitik, umumiy holda esa sonli yechimni qabul qiladi.
Bu yechimlar laboratoriya tajribalarini tavsiflash uchun ishlatiladi [16,17,74].
18](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_18.png)


![Ba'zan chegaraviy holatda (1.15) dispersiv uzatish hisobga olinmaydi. Keyin bu
shart soddalashtiriladic(t,0)=c0.
(1.16)
G'ovakli muhitdagi zarrachalarning harakatini ikki komponentga bo'lish
mumkin: birinchisi- doimiy tezlikdagi konvektiv harakat, ikkinchisi- konvektiv
ko’chish bilan bir xil tezlikda harakatlanadigan ko’chish fronti bo'ylab tasodifiy
dispersiv ko’chish. Muhitning chiqish uchini tark etgan zarracha muhitga
qaytmaydi, deb taxmin qilinadi. Bu muhitning chiqish uchida dispersiya
yo'qligini anglatadi.
x= L
∂c(t,L)
∂x
=0.
(1.17)
(1.14) – (1.17) kabi shartlar bilan (1.12), (1.13) yechimni chiziqli holat uchun
analitik yo l bilan olish mumkin.
ʻ
Agar zarrachalarni (moddani) cho'ktirish yoki chiqarish ta'siri bo'lmasa, (1.12),
(1.13) tenglamalar soddalashtiriladi. Bu holda massa saqlanish tenglamasini
quyidagicha yozish mumkin
∂c
∂t
+∇ ⋅(⃗vc)+∇ ⃗J= r,
(1.18)
bu yerda
⃗v - filtrlash tezligi vektori, ⃗J - dispersiv massa oqimi va r - moddaning
massa ko’chish intensivligi [6].
(1.18) dagi filtrlash tezligi odatda doimiy qiymat sifatida belgilanadi yoki
suyuqlik harakati tenglamalaridan aniqlanadi.
Moddaning dispersiv oqimi
⃗J boshqa ko’chish xususiyatlari bilan bog'liq
bo'lishi kerak. Odatda bu munosabat umumlashtirilgan Fick qonuni sifatida
beriladi
21](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_21.png)
![⃗J= D⋅∇ c, (1.19)
bu yerda D
‒ dispersiya tenzori.
Dispersiya tenzori moddaning kontsentratsiyasiga va uning gradientiga bog'liq
emas, ammo bu filtrlash tezligiga bog'liq [13]
D = (D m+αTv)I+(αL− αT)
⃗vT
v
, (1.20)
Bu yerda
Dm - molekulyar diffuziyaning samarali koeffitsienti, αT, αL -
ko'ndalang va bo’ylama dispersiyalar, I - birlik tenzori, v vektorning qiymati
⃗v ,
T ustki belgisi
⃗v vektor transpozitsiyasini bildiradi. Odatda αT, αL muhit
xossalarini xarakterlovchi konstantalardir.
(1.18), (1.19) tenglamalardan passiv (konservativ) moddani olamiz.
∂c
∂t
+∇ ⋅(⃗vc)= ∇ ⋅(D⋅∇ c).
(1.21)
(1.20) bilan (1.21) tenglama laboratoriyada yaratilishi mumkin bo'lgan bir
jinsli g'ovakli muhitlar uchun qoniqarli natijalar beradi. Biroq, amalda barcha
real muhitlar bir jinsli emas, ular uchun (1.21), (1.20) tenglamadan foydalanish
mumkin. Haqiqiy muhitning kichik va katta miqyosdagi bir jinsli bo'lmaganligi
moddalarning ko’chish qonunining Fik qonunidan chetga chiqishining asosiy
sababidir [50]. Bundan tashqari, (1.21) tenglama parabolik turga tegishli bo'lib,
u cheksiz tebranishning tarqalish tezligi bilan tavsiflanadi, ya'ni
kontsentratsiyaning buzilishlari cheksiz tezlikda tarqaladi, bu fizik nuqtai
nazardan noto'g'ri faktdir.
Juda tez-tez dispersiya koeffitsientlari
αT, αL doimiy bo'lmagan qiymatlar
sifatida qabul qilinadi, lekin filtrlash tezligiga bog'liq. Boshqa hollarda, ular
koordinatali
x va t vaqtga bog'liq deb hisoblanadi . Katta x va t ular asimptotik
qiymatlariga yetadi [28, 66].
22](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_22.png)
![⃗J va ∇с o'rtasidagi chiziqli munosabatlar (1.19) buzilgan yondashuv ham
mavjud. Masalan, yuqori konsentratsiyali aralashmalar uchun chiziqli bo'lmagan
munosabatni kuzatish mumkin [51]. Ayrim adabiyotlarda
⃗J o‘zgarishda
xotiraning ta’siri hisobga olingan. Bunda (1.19) ga nisbatan
⃗J differentsial
tenglama sifatida ifodalanadi. Umumiyroq holatda (1.21) o rniga (1.19), (1.20)
ʻ
umumlashgan bog liqliklar qo llanilganda integrodifferensial tenglamalar
ʻ ʻ
olinadi. Bunday nazariyalar "nolokal" deb ataladi, bunda muhitning
dispersiyaviy xossalari harakat tarixiga va muhitning barcha nuqtalarida
kontsentratsiya gradientiga bog'liq. E'tibor bering, materiyaning o'tish
nazariyasida anomal ta'sirlarni tavsiflash uchun bunday yondashuvlar ancha vaqt
oldin qo'llanilgan. Masalan, [90] da avtokorrelyatsiya nazariyasi taklif qilingan
bo'lib, uning asosida moddalarni uzatish tenglamasi olingan bo'lib, u bir
o'lchovli ko’rinishga ega.
∂c
∂t+v∂c
∂x− D ∂2c
∂x2= − A (
∂2c
∂t2+2v ∂2c
∂t∂x+2v∂2c
∂x2),
(1.22)
bu yerda A yangi doimiy,
D= αLv, A= β/v , β muhit xususiyatini tavsiflovchi
doimiy hisoblanadi.
(1.22) tenglama (1.18) ko'rinishga ega bo’ladi, agar (1.19) o'rniga biz (skalar
shaklda) olsak.
J=− D ∂c
∂x
− A ∂J
∂t
− Av ∂J
∂x
.
(1.23)
Quyida, kichik miqyosda bir jinsli bo’lmagan muhitlar taklif qilingan
⃗J=− D⋅∇ c− A⋅∂⃗J
∂t
,
(1.24)
bu yerda A tenzor bo'lib, u A koeffitsientining uch o'lchovli ekvivalenti
hisoblanadi.
23](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_23.png)
![Shubhasiz, (1.24), (1.23) ning maxsus holatidir. Xuddi shunday (1.24) uchun
(1.22) o'rniga quyidagi uzatish tenglamasini olamiz∂с
∂t+v∂c
∂x− D ∂2c
∂x2= − A (
∂2c
∂t2+2v ∂2c
∂t∂x).
[50] da suyuqlik oqimi va dispersiyasining yangi termodinamik nazariyasi
asosida olingan yuqoridagilarni umumlashtiruvchi umumiyroq bog liqlik
ʻ
keltirilgan. Bu nazariya muallifning boshqa asarlarida ham keltirilgan [50], ya'ni
[48, 49]. [50] ning asosiy xulosasi shundan iboratki, dispersiya tenglamalari
suyuqlikning g’ovak muhitdagi harakati tenglamasidan Darsi qonuni olingani
kabi g’ovak muhitdagi moddaning ko’chishi tenglamalaridan ham olinishi
mumkin.
Keling, (1.12) xususiy holatni bir o’lchovli konvektiv a’zo va moddaning
massa almashinuvini hisobga olmagan holda ko'rib chiqaylik.
∂c
∂t
=− ∂
∂x
(J).
(1.25)
Ma'lumki, Fick diffuziyasi holatida moddaning diffuziya oqimi
quyidagicha aniqlanadi.
J=− D(m)∂c
∂x
,
(1.26)
Bu yerda
D(m) - molekulyar diffuziya koeffitsienti .
Quyidagi o'lchamsiz o'zgaruvchilarni kiritamiz
X = x
x0
, τ= t
t0
, c= c
c0
, bu
yerda
x0, t0,c0 - xarakterli uzunlik, vaqt va konsentratsiya, mos ravishda (1.20)
ni (1.25) ga almashtirib, o'lchamsiz o'zgaruvchilarga o'tamiz
1
t0
∂c
∂τ= 1
x0
2
∂
∂X (D (m)∂c
∂X ).
(1.27)
24](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_24.png)
![O'lchovsiz tenglama (1.27) mos keladigan o'lchovli tenglama bilan bir xil
shaklni saqlab qolishi uchun masshtablar τ0 va x0 o'zaro bog'liqligi kerak
τ0~x0
2.
Oxirgi munosabat Fick diffuziyasi uchun xosdir. Biroq, fraktal
tuzilishga ega bo'lgan muhitlarda o'tkazilgan ko'plab tajribalar bu
munosabatlarni qoniqtirmasligini ko'rsatadi [52]. O’rta kvadrat siljishi vaqtga
quyidagicha bog'liqligi ko'rsatilgan
¿x2>~t
2
2+θ,
(1.28)
bu erda
θ - anomal diffuziya indeksi deyiladi.
(1.28) ni hisobga olib, (1.27) da korrelyatsiyani qo’llaymiz
x0
2~t
2
2+θ.
(1.29)
Ko'rinib turibdiki,
θ=0 (1.29) dan Fick diffuziyasiga kelamiz.
Masshtablash munosabati (1.29) qanoatlantiriladigan diffuziya tenglamasini
olish uchun
J massa oqimi munosabati mos ravishda o'zgartirilishi kerak.
Bunday holda, Fik qonuni
θ=0 dagi o'zgartirilgan munosabatdan kelib chiqishi
aniq. Tabiiyki, bunday o'zgartirishlar har xil bo'lishi mumkin, shunga ko'ra turli
xil diffuziya tenglamalarini olish mumkin. Ikkita ma'lum modifikatsiya [39] da
keltirilgan. Ulardan birinchisi diffuziya koeffitsientining quyidagicha o'zgarishi
bilan bog'liq [72].
D(m)(x)= D fx−θ,
(1.30)
bu yerda
Df - doimiy samarali diffuziya koeffitsienti.
(1.30) dan foydalanib quyidagi diffuziya tenglamasiga kelamiz
∂c
∂t
= ∂
∂x(D fx−θ∂c
∂x).
(1.31)
25](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_25.png)
![(1.31) tenglama uchun (1.29) munosabat bajariladi.
Anomal diffuziya indeksi θ muhitning fraktal o'lchamiga bog'liq df .
Yana bir modifikatsiya massa oqimining
J modifikatsiyasi bilan bog'liq
bo'lib, u koordinatadan kontsentratsiyaning
θ+1 -chi tartibli kasr hosilasi bilan
mutanosib hisoblanadi, Va bu holda (1.29) munosabat qanoatlantiriladi. Biroq,
differensial tenglamaning tartibi
2+θ ga teng bo'ladi , bu esa masalalarni
qo'yishda qo'shimcha muammolarni keltirib chiqaradi. Shuning uchun
tenglamaning tartibi 2 ga teng yoki undan kichik bo'lishi kerak. Bunga (1.26)
modifikatsiyadan so'ng hosila tartibi 1 ga teng yoki undan kam bo'lganligi bilan
erishiladi. (1.29) munosabatni bajarish talabi vaqt bo'yicha qo'shimcha kasr
hosilalarini kiritishni talab qiladi, bu esa
J ning o'zgarishida lokal bo'lmagan
ta'sirlarni tavsiflaydi . Bunday ta'sirlar, xususan, [29, 55, 70] da qayd etilgan va
o'rganilgan. Demak, massa oqimi quyidagi shaklda berilishi mumkin
J= D f∂t
1−γ
(
∂βc
∂xβ),γ>0, β<1,
(1.32)
Bu yerda
γ va β mos ravishda vaqt va fazo o'zgaruvchisiga nisbatan
hosilalarning tartibini aniqlaydi.
(1.32) dagi kasr hosilalari tegishli integral tasvirlar bilan aniqlanadi [88].
∂x
βc= ∂βc
∂xβ=∫
0
x
(x− ξ)−β
Г (1− β)
∂c
∂ξ
dξ ,
∂t
γc= ∂γc
∂xγ=∫
0
t
(t− ξ)−γ
Г (1− γ)
∂c
∂ξ
dξ ,
Bu yerda
Г(х) - gamma funksiyasi.
(1.32) ni (1.25) o rniga qo yish orqali quyidagi hosil bo’ladi
ʻ ʻ
∂c
∂t= ∂
∂x(D f∂t
1−γ
(
∂βc
∂xβ)),
(1.33)
26](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_26.png)
![bunda hosilalarning tartiblari γ va β (1.29) munosabat qanoatlantiriladigan
tarzda tanlanishi kerak. Bu talab quydagicha bo’ladi
t0~x(1+β)/γ.
(1.34)
(1.34) ni (1.29) bilan solishtirsak, quyidagini olamiz
θ+2= 1+ β
γ
.
(1.35)
(1.33) ning ikkala qismiga kasr integrallash amalini qo’llasak, quyidagi
tenglamani olamiz.
∂γc
∂tγ= ∂
∂x(D f
∂βc
∂xβ).
(1.36)
Tartibsiz muhitlarda, yuqorida ta'kidlanganidek, moddaning tarqalishi
anomal ta'sirlarning namoyon bo'lishi bilan sodir bo'ladi va anomaliyaning
mumkin bo'lgan sabablaridan biri g'ovakli muhit strukturasining bir jinsli
emasligidir. YG’M ni shunday vosita deb hisoblash mumkin. Ba'zi ishlarda
suyuqlikning muallaq va erigan moddalar bilan birgalikda yoriqlar va g'ovakli
bloklarda alohida oqishini hisobga olgan holda, moddalarni o'tkazish modellari
taklif qilinadi va anomal effektlar o'rganiladi. [40] da modda
kontsentratsiyasining kasr hosilalarini vaqt bo'yicha ham, koordinatalarda ham
ishlatadigan, yoriqlar va tasodifiy taqsimlangan g'ovakli bloklar o'rtasidagi
moddalar almashinuvini, sekinlashuv ta'sirini hisobga oladigan modellardan biri
taklif qilingan. Muhitning kirish chegarasida ixtiyoriy, vaqtga bog'liq chegara
sharti uchun YG’M va atrof-muhitdagi moddalar konsentratsiyasi uchun analitik
yechimlar olinadi. Moddaning g'ovakli bloklarga anomal tarqalishi bilan bir
qatorda, o'tkazish jarayonida atrof-muhitga diffuziya muhim rol o'ynashi
ko'rsatilgan.
27](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_27.png)
![YG’Mda muhitning o'zaro ta'sir qiluvchi faol modda bilan aralashma
kiritilganda, o'tkazish xususiyatlari juda katta farq qilishi mumkin bo'lgan zona
paydo bo'lishi mumkin. Umuman olganda, YG’Mda moddani yoriqlar bo'ylab
ancha masofaga ko’chish mumkin, shu bilan birga moddaning g'ovakli bloklarga
tarqalishi bir vaqtning o'zida sodir bo'ladi. Moddaning yoriqlardan g'ovakli
bloklarga diffuziya ko’chishi sezilarli bo'lishi mumkin bo'lgan sekinlashuv
hodisalariga olib keladi [71]. Yoriq atrofida o'zgargan zona, xususan, karbonatli
YG’Mlarda, faol modda yoriq joyni o'rab turgan tog 'jinslari bilan o'zaro
ta'sirlashganda, uni eritishi mumkin bo'lganida paydo bo'lishi mumkin [75, 81].
G'ovakli bloklarga diffuziyani klassik Fick qonuni bilan tavsiflash mumkin.
Biroq, bir jinsli bo'lmagan bloklar uchun, ayniqsa moddaning tog jinsi bilan
o'zaro ta'sirini hisobga olgan holda, Fick qonuni buziladi. (1.36) tenglama
anomal hodisalarni hisobga olgan holda diffuziya jarayonini tavsiflash uchun
ishlatilishi mumkin.
[37] da moddaning tog jinslari bilan o zaro ta siri natijasida tuzilishiniʻ ʻ ʼ
o zgartirishi mumkin bo lgan atrof muhit bilan bir yoriqlikdagi diffuziya
ʻ ʻ
masalasi ko rib chiqilgan.
ʻ
Ba'zi ishlarda erigan moddalar bo'lgan sovuq suvni YG’Mga quyish
muammolari tahlil qilingan. Issiqlik va moddaning ko’chishi jarayonida ham
anomal hodisalar hisobga olinadi. Modellashtirishda kasr hosilali tenglamalar
bilan amalga oshiriladi.
Yuqoridagi qisqacha sharhdan ko'rinib turibdiki, moddalarni bir jinsli
bo'lmagan muhitda ko’chish vaqtida anomal hodisalarni modellashtirishda turli
xil yondashuvlar mavjud. Anomaliya effektlarini tavsiflashning samarali
usullaridan biri kasr hosilalari bilan differensial tenglamalardan ham vaqt, ham
fazoda bo’yicha hosilalar hisoblanadi. Keyinchalik ushbu ishda ushbu
yondashuv moddalarni bir jinsli bo'lmagan muhitda ko’chishning turli
masalalarini hal qilish uchun ishlatiladi.
28](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_28.png)
![1.3. Yoriq-g'ovak muhitda anomal modda ko’chish jarayonlarini
modellashtirish.
Ma’lumki, Fik qonuni diffuziya oqimi va modda konsentratsiyasi
gradienti o‘rtasida proportsional bog‘lanishni o‘rnatadi [13, 35]. Bunda moddani
konvektiv ko’chishning tenglamasi olinadi, uning yechimi turli boshlang'ich va
chegaraviy shartlar uchun olingan. Xususan, impulsiv chegara sharoitlari uchun
bir jinsli muhitda Gauss taqsimot funksiyasi shakliga ega bo'lgan siljish egri
chiziqlari olinadi. Biroq, bir qator holatlar uchun bunday model shartlari
buziladi. Bunday holda, ko'pincha ikkita qoidabuzarlik aniqlanadi: 1)
kontsentratsiya profillarining nisbatan tez o’sishi, 2) dum, ya'ni siljish egri
chiziqlarining tushuvchi qismining nisbiy uzayishi. Bu anomaliyaning
natijasidir, ya'ni moddaning fick bo'lmagan ko’chishi.
Haqiqiy suv omborlarida va laboratoriya tajribalarini o'tkazishda
moddalarning ko’chining anomal tabiati ko'pincha kuzatiladi, buni klassik Fick
qonuniga asoslangan an'anaviy modellar doirasida tasvirlash qiyin. So'nggi
vaqtlarda adabiyotda klassik Fik qonuni [39] asosida qurilmagan moddaning
diffuziya ko’chishining yangi matematik modellari berilgan bir qator ishlar
paydo bo'ldi. Suyuqlikda muallaq kichik zarralar, turli kuchlar ta'sirida g'ovak
bo'shlig'ida harakatlanayotganda, harakatning murakkab traektoriyasiga ega
bo'lishi mumkin. Berilgan zarrachaning ma'lum bir nuqtada vaqtning ma'lum bir
nuqtasida bo'lish ehtimoli normal taqsimotga ega bo'lolmaydi, shuning uchun
klassik Fick nazariyasidan foydalanish yetarli asosga ega emas. Bunday
vaziyatda, [18,20,70] da ko'rsatilganidek, ehtimollik modellaridan
foydalanganda, ehtimollik zichligi vaqt va fazoviy koordinata bo'yicha kasr
hosilalarini o'z ichiga olgan tenglamalarni qanoatlantiradi.
Yoriq g’ovak muhit (YG’M) juda murakkab tuzilishga ega va ko'pincha
fraktallar deb hisoblanadi. Yoriqlar va g'ovak bloklarning murakkab tuzilishi
natijasida muallaq zarrachalarning trayektoriyasi ham murakkab tuzilishga ega.
Bunday muhitda moddalarni uzatishning birinchi modellaridan biri [38] da
29](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_29.png)
![ko’rsatilgan. Bicontinuum yondashuvi [11] doirasida kasr hosilalarni o'z ichiga
olgan YG’Mda konvektiv tashish tenglamalari analitik tarzda olinadi.
Tenglamalar YG’Mda moddalarni uzatish jarayonlarini tahlil qilish uchun
ishlatilgan [37,40].
Fraktal tuzilishga ega muhitda diffuziya jarayonlarini modellashtirishga
turli yondashuvlar [21,42,72] da keltirilgan. Muammoning holatining nisbatan
batafsil tahlili [52] da keltirilgan.
Yer osti suv havzalarining ifloslanishi atrof-muhitni muhofaza qilishda
katta muammo hisoblanadi. Ifloslantiruvchi moddalar har xil tabiatga ega
bo'lishi mumkin - organik birikmalar, og'ir metallar, radioaktiv moddalar, turli
sanoat chiqindilari va boshqalar [34,36]. Ko'pgina yer osti suv omborlari yoriq
g’ovakli yoki sof yoriq tipga ega. Birinchisida yoriqlar bilan kesilgan g’ovak
bloklar g’ovakli va o'tkazuvchan, ikkinchisida esa ular g’ovakli emas (bir oz
g’ovakli, shuning uchun suv o'tkazmaydigan). Yoriqlar odatda fraktal tuzilishga
ega va nisbatan yaxshi o'tkazuvchandir [40,41]. YG’Mda asosiy suyuqlik
zahiralari g’ovakli bloklarda joylashgan va yoriqlar harakatning asosiy kanallari
hisoblanadi. Bu xususiyatlar jarayonni matematik modellashtirishning asosini
tashkil qilishi kerak.
So'nggi vaqtlarda fraktal tuzilishga ega bo'lgan muhitda diffuziya
jarayoniga katta e'tibor berilmoqda [52]. [42] da, fraktal geometriyaga ega
bo'lgan bir jinsli bo'lmagan g'ovakli muhitda bir jinsli bo'lmagan suyuqlik oqimi
uchun fraktal kechikish vaqtiga ega nisbatan oddiy model taklif qilingan. Bir
jinsli bo lmagan muhitda moddalarni tashish bo yicha olib borilgan dalaʻ ʻ
eksperimental tadqiqotlarida [14,84] moddaning konsentratsiya profillari klassik
Fik qonuniga qaraganda tezroq harakatlanishi, assimetriya va tik oldingi chetiga
ega ekanligi aniqlandi. Bu ta'sirlarni klassik Fik qonuni va mos keladigan massa
uzatish tenglamasi doirasida tasvirlab bo'lmaydi. Kuchli bir jinsli bo lmagan
ʻ
muhitda moddalarning o tkazilishining anomal xarakterini kasr hosilalari bilan
ʻ
differensial tenglamalar yordamida modellashtirish mumkinligi ko rsatilgan
ʻ
30](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_30.png)
![[10,19,53]. Xususan, quyida, massa balansi tenglamasiga vaqtga nisbatan
konsentratsiyaning kasr hosilasi bilan qo'shimcha atamaning kiritilishi ikki
zonali yondashuvlar nuqtai nazaridan tushuntirilgan, bunda moddaning
harakatchan zonadan ko’chishi statsionar suyuqlik bo'lgan zonaga turli
intensivlikda sodir bo'ladi [27, 44, 45].
YG’Mda moddalarni ko’chishining eng oddiy modellari individual yoriq
va uni o'rab turgan g'ovakli muhitni o'rganish bilan bog'liq. Bunday muhitda
moddaning ko’chishini eksperimental tadqiqotlar [82] ko'rsatadiki, uzun dum
shakllanishi joy almashish egri chizig'ida topiladi. Bu Darsi qonuni buzilganda
va Forxxaymer qonuni ishlaganda, yoriq atrofida chegara qatlami mavjudligi va
yuqori oqim tezligi bilan izohlanadi. Eksperimental joy almashish egri chiziqlari
ikki zonali yondashuv [25,78,79] yordamida ishlangan, ya'ni birida suyuqlik
harakatchan, ikkinchisida esa harakatsiz bo'lgan ikki qonunga ega muhitni ko'rib
chiqadigan. Ushbu model asosida tuzilgan eksperimental va nazariy siljish egri
chiziqlari o'rtasida yaxshi natijaga erishiladi.
Anomal modda ko’chishi Fickning chiziqli bo'lmagan qonuni ko'rinishida
ham namoyon bo'lishi mumkin [51]. Suyuqlikda yuqori konsentratsiyali
moddalar bo'lsa, moddalar oqimining zichligi va kontsentratsiya gradienti
o'rtasidagi chiziqli bog'liqlik buziladi. Eksperimental ma'lumotlarni qayta
ishlash shuni ko'rsatadiki, moddaning past konsentratsiyasida Fick qonuni
qoniqarli ishlaydi. Biroq, yuqori konsentratsiyalar uchun eksperimental
ma'lumotlarning yaxshi tavsifini faqat chiziqli bo'lmagan nazariya yordamida
olish mumkin. Xuddi shunday xulosalar turli omillarning ko'rsatilgan model
parametrlariga ta'siri bilan izohlangan.
Anomal hodisalarni hisobga olish uchun Fick qonuni ba’zan inertial atama
– modda oqimi zichligining vaqt hosilasini ham o‘z ichiga oladi [9,50,61].
Bunday holda, moddalarni ko’chishi giperbolik tenglamalari olinadi, ular
kontsentratsiya profillarining tarqalish tezligining cheklanganlik xususiyatiga
ega, ya'ni kontsentratsiya to'lqinlari hosil bo'ladi. Makroskopik modellashtirish
31](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_31.png)
![asosida modda oqimi zichligining bo'shashish vaqti juda qisqa ekanligi
ko'rsatilgan. [61] da turli parametrlarning differensiallanishiga qarab,
konsentratsiya to lqinlarining tarqalish xarakteristikalari ham har xil bo lganʻ ʻ
turli uzatish qonunlarini olish mumkinligi ko rsatilgan.
ʻ
Bir qator ishlar g'ovak muhitda modda va suyuqlikning ko’chish
qonuniyatlarida xotira effektlarini hisobga olishga bag'ishlangan. [23,43] da
Darsi qonuni xotira effektlarini kiritish uchun umumlashtiriladi. Suyuqlik
bosimini uning zichligiga bog'lovchi umumiy holat tenglamasi ham qabul
qilinadi. Tajriba natijalari tavsiya etilgan modellar yordamida tavsiflanadi. Shuni
ta'kidlash kerakki, g'ovakli muhitda suyuqlik harakati paytida xotira
effektlarining namoyon bo'lishi g'ovak bo'shlig'ida moddalarning ko’chishi va
massa almashinuvi jarayonlari bilan bog'liq bo'lishi mumkin . Shunday qilib,
o’tirgan zarralar suyuqlik o'rniga harakat qilganda, g'ovaklarga joylashadigan
ba'zi zarralar ularning hajmini kamaytirishi va ba'zan ularni yopishi mumkin,
ularning ba'zilari g'ovakli muhit skeleti bilan kimyoviy yoki fizik ta'sirga
kirishishi mumkin. G'ovak bo'shlig'i tuzilishining o'zgarishiga olib keladi.
Bularning barchasi muhitning o'tkazuvchanligining o'zgarishiga olib keladi va
bu o'z navbatida, suyuqlik harakatlanayotganda xotira effektlarining namoyon
bo'lishiga olib keladi. [43,57] da xotira effektlarining namoyon bo'lishini
ko'rsatuvchi eksperimental tadqiqotlar natijalari keltirilgan. Holat va filtratsiya
qonunlarining tenglamalari vaqt bo'yicha oqimning asosiy xarakteristikasining
kasr hosilalarini o'z ichiga oladi. Tajriba natijalarini qayta ishlash hosilalarning
tartibini birlikdan ancha kichik chegaralar ichida beradi. Bu
0,12 ÷0,37 xotira
effektlarining roli katta ekanligini ko`rsatadi.
Sierpinski sohasida tartibsiz muhitda diffuziya ko'rib chiqiladi. Suyuqlik
va moddalarning fraktal tuzilishga ega bo'lgan muhitda ko’chishi perkolatsiya
nazariyasi bilan chambarchas bog'liqdir [85,86].
Shuni ta'kidlash kerakki, erigan moddalar va suyuqlikda muallaq kolloid
zarrachalarni ko’chishni modellashtirishga yondashuvlar g'ovakli muhitlarda
32](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_32.png)
![o'xshashdir. An'anaviy modellar muvozanat tenglamasidan va g'ovaklardagi
moddalarning cho'kishi (cho'kishi) kinetikasidan iborat. Balans tenglamasi
odatda konvektiv diffuziya tenglamasidan, zarracha (yoki erigan moddalar)
oqimi konvektiv va dispersiv oqimlar yig'indisidan iborat. Zarrachalarning
cho'kish va ajralish kinetikasi uchun ham turli xil tenglamalar mavjud. Bir qator
ishlarda eksperimental ma'lumotlarni klassik ko’chish modellari bo'yicha
tavsiflash amalga oshirildi. Biroq, bir jinsli bo’lmagan muhitlar uchun bunday
modellar odatda yaxshi natijalar bermaydi. Bunday bir jinsli bo’lmagan muhitlar
anomal effektlar paydo bo'lishi mumkin, ular uchun yuqorida tavsiflangan
yondashuvlar modellashtirish uchun ishlatilishi mumkin.
Klassik modellarga muvofiq, muhitning chiqish joyidagi siljish egri
chiziqlari suyuqlik teshiklarning biror hajmidan o’tgandan keyin paydo bo'ladi.
Biroq, bu shart har doim ham qondirilmaydi, qattiq zarrachalar va
polimerlarning ba'zi suspenziyalari uchun bunday og'ish [12, 65, 106] da
kuzatilgan. Bu shuni anglatadiki, fenomenologik modellar suspenziya filtrlash
mexanizmlarini to'g'ri, umumlashtirmaydi va universal tarzda tavsiflay olmaydi.
Bunday vaziyatda modellashtirishning mumkin bo'lgan va samarali usullaridan
biri mikrogrid modellaridan foydalanish bo'lishi mumkin. Bunday modellarning
ayrimlari [15,76,77] da taklif qilingan. Yangi populyatsiya balansi modelida
qayta tavsiflangan bo'lib, u zarrachalar oqimining kamayishi, g'ovak
bo'shlig'ining selektivligini hisobga oladi (katta o'lchamdagi zarralar uchun ba'zi
g’ovaklardan o'tib bo'lmaydi, nisbatan kichikroq bo'lgan zarralar uchun ular
o'tish mumkin). Olingan yechimlar siljish egri chiziqlari klassiklardan sezilarli
darajada og'ishini ko'rsatadi. Umuman olganda, fenomenologik modellar bilan
bir qatorda statik (stokastik) modellashtirishdan ham samarali foydalanish
mumkin.
Taqdim etilgan qisqacha sharh shuni ko'rsatadiki, moddaning bir jinsli
bo'lmagan g'ovakli muhitda anomal tarqalishi (dispersiyasi) moddalarni ko’chish
jarayonlarini tahlil qilishda hal qiluvchi ahamiyatga ega bo'lishi mumkin. Shu
33](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_33.png)

![§1.2 da ta'kidlanganidek, moddaning bir jinsli bo'lmagan muhitda anomal
ko'chishi vaqt va fazoda kasr hosilalarini o'z ichiga olgan tenglamalar bilan
tavsiflanadi. Bu tenglamalarni yechish uchun kasr hosilalari funksiyalarning o‘zi
yoki ularning butun tartibli hosilalari bilan ifodalanishi kerak. Asosan, chiziqli
masalalar uchun operatsion usul, xususan, Laplas o'zgartirishlar usuli
qo'llanilishi mumkin. Ammo, umumiy holatda, sonli usullar, xususan, chekli
ayirmalar usuli qo'llaniladi. Shuning uchun kasr hosilalarini diskretlashtirish
masalalari muhim ahamiyat kasb etadi. Quyida ushbu masalaga oydinlik
kiritadigan ba'zi ma'lumotlar mavjud. Oddiy ko’chish masalasi uchun turli xil
yechim usullarini qo'llash imkoniyati haqida to'xtalmaymiz . Kasr hosilalari
bo'lgan tenglamalarni yechish usullari haqida ma'lumot beraylik.
[40] da transformatsiyalar guruhlari ortidan moddaning ko’chish masalasi
boshlang ich va chegaraviy shartlarga ega (o lchamsiz birliklarda) quyidagiʻ ʻ
tenglama ko’rinishda keltiriladi:
∂C
∂t+b∂γC
∂tγ+∂βC
∂tβ=− ∂C
∂X , 0<X <∞ ,
(2.1)
C(0,X )=0
(2.2)
C(t,0)=c0(t),
(2.3)
bu yerda
c0(t) - berilgan funksiya.
(2.1) (2.3) masala
‒ t o zgaruvchiga nisbatan Laplas konvertatsiyasi ʻ
yordamida yechiladi . O'zgartirishlarda tenglama olinadi
d¯c
dX
= − ¯c(s+bs γ+sβ),
(2.4)
¯c(0)= ¯c0,
(2.5)
bu yerda
¯c= L(c), L - Laplas o'zgartirish operatori .
35](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_35.png)
![(2.4) yechim (2.5) ko'rinishga ega¯c= s¯c0¯ϕ(s,X )exp (− Xs ),
(2.6)
bu yerda
¯ϕ(s,X )= 1
s
exp [− (sβ +bs γ)X ].
(2.6) dan quyidagiga kelamiz
C(t,X )= ∂
∂t∫
0
t
c0(t−τ)χ(τ− X )ϕ(τ− X ,X )dτ ,
(2.7)
Bu yerda
χ(τ) Heaviside birligi funktsiyasi ,
ϕ(t,X)=1−
1
π
∫
0
∞
exp [−ξt−X(bξ
γ
cos (πγ)+ξ
β
cos (πβ))]׿¿×sin [X(bξ
γ
sin(πγ)+ξ
β
sin(πβ))]
dξ
ξ
.
Xususiy holatda, (2.7) dan
c0(t)=1 bo’lganda quyidagiga kelamiz
C (t,X )= χ(t− X )ϕ(t− X ,X ).
(2.8)
(2.8) dan
γ= 1
2
, β= 1
2 uchun quydagicha
C (t,X )= χ(t− X )erfc [
X (1+b)
2√t− X ].
Adsorbsiya, zarrachalarning cho'kishi va g'ovaklarning zarrachalardan
ajralib chiqish hodisalarini hisobga olgan holda bir jinsli bo'lmagan muhitda
moddalarni ko’chishi uchun eng oddiy holatlarda (chiziqli sorbsiya izotermlari,
sorbsiyaning chiziqli kinetikasi, tiqilib qolish va suffuziyaning chiziqli
kinetikasi va boshqalar) chiziqli shaklga ega bo'lgan ko’chish tenglamalari
tizimlari ham olinadi [24,39]. Bu tenglamalarni yechish uchun ba'zi analitik
yechish usullarini, masalan, Laplas o'zgartirishlar usulini ham qo'llash mumkin.
36](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_36.png)

![C1(t,Y)= ∑
k=0
∞
U k(t,Y)εk,C2(t,Y)= ∑
k=0
∞
Vk(t,Y)εk,bu yerda
Uk(t,Y),Vk(t,Y) - noma'lum funktsiyalar.
Suyuqlik oqimi bilan bog'liq masalalar uchun, xotira effektlarini hisobga
olgan holda, filtratsiya qonuni uchun ham, suyuqlik zichligiga bosim bilan
bog'liq bo'lgan holat tenglamasi uchun ham kasr hosilalari ishlatilgan.
Demak [23,43] Darsi qonuni va holat tenglamasida
⃗q=−D ∇ p,
(2.16)
p= Gρ ,
(2.17)
bu yerda
⃗q - suyuqlik massasi oqimi, p - bosim, ρ - suyuqlik zichligi, D -
filtrlash koeffitsienti,
G - koeffitsient, xotira effektlarini hisobga olgan holda
yoziladi.
f1(t)∗⃗q=− f2(t)∗∇ p,
(2.18)
ϕ1(t)∗ p= ϕ2(t)∗ρ,
(2.19)
Bu yerda
f1(t),f2(t),ϕ1(t),ϕ2(t) -integro-differensial operatorlar va ¿ vositalar
f(t)∗g(t)=∫
0
t
f(t−ξ)g(ξ)dξ .
(2.18), (2.19) munosabatlari quydagi ko’rinishga keltiriladi
(γ+ε ∂n1
∂tn1)⃗q= −(c+d ∂n2
∂tn2)∇ p,
(2.20)
(a+b ∂m1
∂tm1)p= − (α+ β ∂m2
∂tm2)ρ,
(2.21)
38](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_38.png)
![bu yerda γ,ε,c,d,a,b,α,β " xotira sozlamalari", ‒ 0≤n1,n2,m1,m2<1.
(2.20), (2.21) da kasr hosilalari Caputo [22] ga muvofiq aniqlanadi.
f(n)(t)= ∂nf(t)
∂tn = 1
Г (1−n)∫
0
t
(t− ξ)−ndf (ξ)
dξ dξ .
(2.22)
⃗q bir o'lchovli holatda aniq, analitik yechim olindi .
Yuqoridagi natijalar kasr hosilalari bilan differensial tenglamalarni
yechishda operativ usulni qo‘llash mumkinligini ko‘rsatadi. Tabiiyki, masala
chiziqli bo'lishi kerak.
Filtrlash qonunida xotiraning ta'sirini hisobga olish uchun biroz
boshqacha yondashuv mavjud. Masalan, [19] adabiyotlarda
v= μ ∂α
∂tα(
∂p
∂x),
(2.23)
bu yerda
α,0≤ α<1 parametr xotira rolini o'ynaydi.
(2.23) natijasida suyuqlikning qovushqoqlik effekti ham xotiraga ega
bo'ladi.
Qayd etilgan yechim usullari o'ziga xos xususiyatga ega, ya'ni ularni kasr
hosilalari bo'lgan umumiy tenglamalarga, xususan, chiziqli bo'lmaganlarga
qo'llash mumkin emas. Shu jihatdan sonli usullar, xususan, chekli ayirmalar
usuli universaldir. Keyinchalik, kasr hosilalari bilan differensial tenglamalarga
ushbu usulni qo'llash imkoniyatlarini ko'rib chiqamiz.
Diffuziya masalalarida kasr hosilalardan foydalanish yaqin yillarda katta
qiziqish uyg'otdi. Xuddi shu ishda kasr hosilalarini yaqinlashtirishning ba'zi
usullari keltirilgan. Diffuziya masalalarida [19,56,73] ishlar kasr hosilalaridan
foydalanishga bag'ishlangan. Kasrli hosilalarni yaqinlashtirish butun tartibli
oddiy hosilalarni yaqinlashtirishga qaraganda qiyinroq. Bu kasr hosilalarining
39](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_39.png)
![lokal bo'lmagan xususiyatga ega ekanligi bilan bog'liq. Berilgan nuqtada
hosilani taxminan hisoblash uchun berilgan nuqta yaqinidagi ma'lumotlardan
foydalanish kerak, hosila hisoblash nuqtasi mintaqa chegarasidan qanchalik
uzoqda bo'lsa, hosilani hisoblash uchun shuncha ko'p hisob ishlatiladi.
Kasr hosilalarini aniqlash uchun ba'zi formulalarni keltiramiz [62]. Kasr
hosilalari uchun eng mashhur ta’rif Rimann-Liuvil formulasi bo'lib, u
quyidagicha x∈[a,b] aniqlanadi.
D RL
α u(x)= 1
Г(n−α)
dn
dx n∫
a
x
u(ξ)(x− ξ)n−α−1dξ ,
(2.24 )
bu yerda
α hosila tartibi, n− 1<α<n,n= [α]+1,[α]− α ning butun qismi.
Yana bir ta'rif - Grunvald-Letnikov formulasi
D GLα = lim
Δx →0
1
Δx α ∑
k=0
[x−a
Δx ]
(− 1)k¿(α¿)¿
¿ ¿¿
(2.25)
bu yerda
α>0 hosila tartibi .
Haqiqiy sonlar to'plamida har bir chegaralangan funksiya
u(x) uchun
(2.24) qator mutlaqo yaqinlashadi.
(2.25) dan foydalanish ko'pincha turg’unmas ayirmali sxemalariga olib
keladi va yaqinlashish aniqligi odatda birinchi tartibdan yuqori emas.
Kasr hosilasining yana bir ta'rifi Kaputo [22] tomonidan taklif qilingan.
Bu (2.22) formula bo'lib, uni (2.24), (2.25) ga o'xshash yozuvda quydagi
ko’rinishda yozamiz.
Dc
αu(x)= 1
Г (n−α)∫
a
x
(x− ξ)n−α−1dnu(ξ)
dx n dξ ,
(2.26)
bu yerda
n− 1<α<n,n= [α]+1.
40](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_40.png)
![(2.26 ) formula (2.24) ga nisbatan bir qator afzalliklarga ega. (2.24) ning
eng mashhur va muhim kamchiligi shundaki, Laplas o'zgartirish usulidan
foydalanganda hosila DRL
α u(x) ning chegara qiymati x=0 pastki chegara
nuqtasida paydo bo'ladi. Bu qiymat ko'pincha muayyan muammolarni hal
qilishda fizik talqinga ega emas. (2.26) formula Laplas o'zgarishlaridan
foydalanganda, aniq fizik ma'noga ega bo'lgan
x= a nuqtadagi butun tartibli
hosila qiymatini beradi. Bundan tashqari, doimo Kaputo hosilasi (2.26) nolga
teng, Rimann-Liouvil hosilasi esa nolga teng emas. Bu Caputo va Riemann-
Liouville hosilalarining o'ziga xos xususiyatlarini tavsiflaydi. Agar
Dc
αu(x) va
DRL
α u(x)
mavjud bo'lsa, [a,b], unda har qanday uchun 1<α<n
tenglik x∈[a,b]
uchun amal qiladi
Dc
αu(x)= D RL
α u(x)− ∑
k=0
n−1dku(a)
dx k
(x− a)−α+k
Г (− α+k+1).
To'r oralig'i
Δx − bo'lgan nuqtalar bilan quyidagi to’rni kiritamiz.
xj= a+ jΔx , j= 0,1 ,...,N ,
Kaputo hosilasining yaqinlashuvini ko'rib chiqamiz
Dc
αu(x)= 1
Г(2−α)∫
a
x
(x− ξ)1−αd2u(ξ)
dξ 2 dξ .
(2.27)
(2.27) dan
xj har bir nuqtada quydagi ko’rinishga kelamiz
Dcαu(xj)= 1
Г (2− α)∑k=0
j−1
∫
xk
xk+1
(xj− ξ)1−αd2u
dξ 2dξ .
(2.28)
Odatdagi
Dc
αu(xj) approksimasiyasi
Dc,1
α,Δx u(xj)= 1
Г (2− α)∑
k=0
j−1u(xk+2)− 2u(xk+1)+u(xk)
Δx 2 ∫
xk
xk+1
(xj− ξ)1−αdξ =
41](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_41.png)
![= 1
Г (2− α)∑
k=0
j−1u(xk+2)− 2u(xk+1)+u(xk)
Δx 2 ⋅Δx 2−α
2− α dj,k=
= Δx −α
Г (3− α)∑
k=0
j−1
(u(xk+2)− 2u(xk+1)+u(xk))dj,k,(2.29)
bu yerda
dj,k=(j− k)2−α−(j− k− 1)2−α.
Approksimasiya (1.59) birinchi darajali
O(Δx ).
Endi ikkinchi tartibli approksimasiyani ko'rib chiqamiz. Buning uchun har
bir nuqtada
xj,j=1,2,...,N−1 ni hisoblashimiz kerak
1
Г(2− α)∫
a
xj
(xj− ξ)1−αd2u(ξ)
dξ 2 dξ .
(2.30)
Integrallarni (2.30) hisoblash uchun funktsiyaning ikkinchi hosilasi tugun
u
nuqtalari Sj(ξ) kiritilgan to'rning tugun nuqtalariga to'g'ri keladigan
xk,k=0,1,...,j
chiziqli splinelar bilan yaqinlashadi. Splayn Sj(ξ), quyidagicha
aniqlanadi.
Sj(ξ)= ∑
k=0
j d2u(xk)
dξ 2 Sj,k(ξ),
(2.31)
bu yerda
Sj,k(ξ) har bir interval uchun [xk−1,xk+1],1≤ k≤ j−1, formulalar bilan
berilgan
S
j,k
(ξ)=¿
{
ξ−xk−1
x
k
−x
k−1
,x
k−1
≤ξ≤x
k
,¿
{
xk+1−ξ
x
k+1
−x
k
,x
k
≤ξ≤x
k+1
,¿¿¿¿
42](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_42.png)
![For k= 0 va k= j,Sk,j(ξ) shaklida berilgan
Sj,0(ξ)=¿
{
x1−ξ
x1−x0
,x0≤ξ≤x1¿¿¿¿ Sj,j(ξ)=¿
{
ξ−xj−1
xj−xj−1
,xj−1≤ξ≤xj¿¿¿¿
Shunday qilib, (2.30) ga yaqinlik quyidagi shaklga ega
1
Г(2− α)∫
a
xj
(xj− ξ)1−αd2u(ξ)
dξ 2 dξ = 1
Г(2− α)∫
a
xj
(xj− ξ)1−αSj(ξ)dξ =
= 1
Г(2− α)∑
k=0
j d2u(xk)
dξ 2 ∫
a
xj
(xj− ξ)1−αSj,k(ξ)dξ = Δx 2−α
Г(4− α)∑
k=0
j d2u(xk)
dξ 2 aj,k,
bu yerda
aj,k= (j− 1)3−α− j2−α(j− 3+α),k= 0,
aj,k= (j− k+1)3−α− 2(j− k)3−α+(j− k− 1)3−α, 1≤ k≤ j− 1,
aj,k=1,k= j.
Natijada, Kaputo hosilasining yaqinlashuvini quyidagicha yozish mumkin
Dc
α,Δx u(xj)= Δx −α
Г (4− α)[aj,0δ0u0+∑
k=1
j
aj,kδ2uk],
(2.32)
bu yerda
δ0,δ2 - quyidagi operatorlar
δ0uj= 2u(xj)− 5u(xj+1)+4u(xj+2)− u(xj+3)
δ2uj= u(xj+1)− 2u(xj)+u(xj−1).
Agar
u(x)∈C3[a,b] va 1<α<2, keyin approksimasiya (2.32) ikkinchi
tartibli bo'ladi, ya'ni
O(Δx 2).
43](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_43.png)
![Shunga o'xshash approksimasiyalarni Riemann-Liouville va Grunvald-
Letnikov hosilalari uchun ham kiritish mumkin. Ammo, kelajakda biz faqat
Caputo lotinlaridan foydalanamiz, shuning uchun bu approksimasiyalar bu yerda
berilmaydi. So'nggi paytlarda asosan Kaputo formulasidan foydalanilganiga
qaramay, Riemann-Liouville, Grunvald-Letnikov kasr hosilalari qo'llaniladigan
ishlar mavjud. Shunday qilib, masalan, [68] da kasr hosilasi bilan parabolik
tenglama uchun qo'yilgan namlikning tarqalishi masalasini sonli hal qilish uchun
quydagi tenglamadan foydalanamiz.∂u(t,x)
∂t = D ∂αu(t,x)
∂xα ,1<α<2
Grunvald-Letnikov hosilasi ishlatilgan.
Quyida konvektiv-diffuziya ko’chishning bir o'lchovli tenglamasi ko'rib
chiqiladi.
∂γc
∂tγ+v∂c
∂x= D ∂αc
∂xα,
(2.33)
Bu yerda
0<γ≤ 1,1<α≤ 2.
(2.33) ni to’r usulida yechish uchun quyidagi to’r kiritiladi:
xj= jh ,h>0,tn= nτ ,τ>0, j=0,1,..., n=0,1,...,
h,τ− x
va vaqt t bo'yicha to’r qadamlari.
Kaputo tomonidan aniqlangan vaqtga nisbatan kasr hosilasi
∂
γ
c(t,x)
∂t
γ =¿
{
1
Г(1−γ)
∫
0
t
(t−ξ)
−γ∂c
∂ξ
dξ ,0<γ<1,¿¿¿¿
(2.34)
To’rning tugun nuqtasida
(tn,xj) (2.34) integral quyidagicha aniqlanadi
44](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_44.png)
![∂γс
∂tγ|(tn,xj)=1
Г(1−γ)∫
0
t
(t−ξ)−γ∂c(ξ,xj)
∂ξ dξ =
1
Г(1−γ)[∑k=0
n−2
∫
tk
tk+1
(tn−ξ)−γ∂c(ξ,xj)
∂ξ dξ +∫
tn−1
tn
(tn−ξ)−γ∂c(ξ,xj)
∂ξ dξ ]=
=1
Г(1−γ)[∑k=0
n−2c(tk+1,xj)−c(tk,xj)
τ ∫
tk
tk+1
(tn−ξ)−γdξ +
c(tn,xj)−c(tn−1,xj)
τ ∫
tn−1
tn
(tn−ξ)−γdξ ]=
=τ1−γ
Г(2−γ)[∑
k=0
n−2c(tk+i,xj)−c(tk,xj)
τ ((n−k)1−γ−(n−k−1)1−γ)+
c(tn,xj)−c(tn−1,xj)
τ ].
(2.35) Vaqtning ma'lum bir nuqtasi uchun
tn c(tk,xj),k=0,1,...,n−1 ma'lum.
Shuning uchun yig'indi ostidagi ifoda ma'lum. Ularni quydagi ko’rinishda
keltirilgan
A= τ1−γ
Г (2− γ)∑
k=0
n−2c(xj,tk+1)− c(xj,tk)
τ ((n− k)1−γ− (n− k− 1)1−γ)
(2.35) ko’rinishda yozish mumkin
∂γc
∂tγ|(tn,xj)= A+
τ−γ
Г(2− γ)
[с(tn,xj)− c(tn−1,xj)].
Approksimasiyalash uchun
∂αc
∂xα ishlatiladi
∂αc
∂xα|(tn,xj)= 1
Г(− α)hα[∑
k=0
j Г (k− α)
Г (k+1)
c(tn−1,xj−k+1)+∑
k=0
n−jГ (k− α)
Г (k+1)
c(tn−1,xn−k)].
Shunga o'xshash approksimasiyalar [75, 76] da ishlatilgan.
Yuqorida keltirilgan materialdan ko'rinib turibdiki, differensial
tenglamalarni kasr hosilalari bilan yechish uchun turli usullardan foydalanish
mumkin. Ko'rib chiqilayotgan muhitning eng universal usuli - bu chekli
ayirmalar usuli. Bundan tashqari, biz turli masalalarni hal qilish uchun ushbu
usuldan foydalanamiz. Bunday holda, yuqorida keltirilgan kasr hosilalarining
yaqinlashuvi qo'llaniladi.
45](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_45.png)
![2.2 . G’ovak muhitda anomal modda ko’chish masalasini yechish
So'nggi vaqtlarda suyuqlik va moddalarning g'ovakli muhitda
ko’chishdagi kechikish ta'sirini o’rganish uchun filtrlash va ko’chish
tenglamalarida koordinata bo'yicha ham, fazoviy o'zgaruvchiga nisbatan ham
kasr hosilalarini hisobga oladigan yondashuv qo'llanildi [2,3,4].
Bu yerda g'ovak muhit ko'rib chiqiladi, shuningdek, moddani ko’chish
tenglamasida moddaning diffuziya oqimi koordinata bo'ylab modda
konsentratsiyasining kasr hosilasi ko'rinishidagi manba a’zosi bilan
modellashtirildi. Bu moddani ko’chish jarayonida anomal hodisalarni hisobga
olish imkonini beradi. Anomal hodisalarni hisobga olmagan holda sohalarning
geometrik xarakteristikalarini ko'rsatmasdan bunday muhitlarda moddalarni
ko’chishining ba'zi muammolari [5-8] da ko'rib chiqilgan.
Tuzilgan shartlarga muvofiq, bir o'lchovli holatda moddaning ko’chishi
quyidagi tenglama tenglama bilan tavsiflanishi mumkin.∂αc
∂tα= D ∂βc
∂xβ+λc
, ( 2.36)
46](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_46.png)
![Bu yerda c- moddaning konsentratsiyasi, t -vaqt с , D – diffuziya koeffitsienti,
мβ/с
, λ – koeffitsient, α,β− hosilalarning tartibi (0<α≤ 1,1< β≤ 2) , bu
bo’limda biz
α= 1 deb tenglamani sonli yechib natijalar olib tahlil qilamiz.
Konsentratsiyali suyuqlik
с0 bilan to'ldirilgan g'ovakli yarim cheksiz
muhit,
t>0 dan boshlab qattiq zarrachalarning hajmli konsentratsiyasiga ega
suspenziyani
с1 kirishi boshlanadi. Yarim cheksizlikda с0 asl konsentratsiya
saqlanib qoladi. Keyin boshlang'ich va chegaraviy shartlar quyidagi ko’rinishga
ega bo'ladi:
c(0,x)= c0, 0≤ x<∞ ,
(2.37)
c(t,0)=c1,c(t,∞ )= c0. (2.38)
(2.36), (2.37), (2.38) masalani yechish uchun chekli ayirmalar usulidan
foydalanamiz [1]. Sohada
D = {0≤ x<∞ ,0≤ t≤ T } biz to'rni kiritamiz, bu
yerda
T jarayon o'rganilayotgan maksimal vaqt. Buning uchun h -qadam bilan
[0,∞)
-oraliq, a[0,T) -interval τ -qadam bilan J qismga bo'linadi. Natijada,
quyidagi to’rni hosil qilamiz:
ωhτ= {(xi,tj),i= 0,1,2 ,..., j= 0,1 ,...,J; xi= ih ; tj= jτ ; τ= T /J}.
Biz (2.36) tenglamani
ωhτ -to'rdagi oshkormas sxemadan foydalanib,
quyidagi ko’rinishda approksimasiya qilamiz.
ci
j+1− ci
j
τ =
D m
RmГ (3− β)h1
β∑
l=0
i−1
w β,1((cm)j−(l−1)
k − 2(cm)i−l
k +(cm)i−(l+1)
k
)+ λc i
j
(2.39)
i= 0,I,j= 1,J− 1
,
bu yerda
w β,l= (l+1)2−β− (l)2−β .
47](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_47.png)



![bu yerda α,β− hosilalarning tartibi (0<α≤ 1,1< β≤ 2) , bu bo’limda biz α= 1
,
β= 2 deb tenglamani sonli yechib natijalar olib tahlil qilamiz.
Teskari masala quyidagicha qo'yiladi.
t∈[t0,t1],t0>0 uchun
z(t)= c(x0,t)
funksiya berilgan, bunda x0 - [0,l] segmentining qandaydir
qo’zg’almas nuqtasi,
c(x,t) esa (2.43)–(2.44) masala yechimidir.
(2.43) tenglamaga boshlang'ich va chegaraviy shartlari odatiy tarzda
berilsin.
Avval
D ni identifikatsiyalash usuli bilan aniqlash masalasini ko'rib
chiqaylik.
x1,x2,...,xn - qatlamning xarakteristik nuqtalari bo’lsin, unda qatlam
bosimining pasayishi o'lchanadi,
zj(t),1≤ j≤ n 0≤ t≤ T lar vaqtning ma’lum
funksiyasi.
J(D )= ∑
k=1
4
∫
0
T
[C (t,xk)− zk(t)]
2dt
. (2.46)
(2.46) funktsional uchun statsionarlik sharti quyidagi shaklga ega bo'ladi
d(J)
d(D)=2∑
k=1
4
∫
0
T
[c(t,xk)− zk(t)]w(t,xk)dt = 0
. (2.47)
Bu yerda
w= ∂C
∂D , c(t,x) - funksiyasini aniqlikning ikkinchi qatoriga DS orqali
yozamiz:
c
S+1
(t,x)≈ c
s
(t,x)+(D s+1− Ds)w
s
(t,x)
. (2.48)
(2.48) tenglamani (2.47) tenglamaga qo’ysak, quyidagi ko’rinishdagi
tenglamaga kelamiz:
51](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_51.png)
![∑
k=1
4
∫
0
T
[c
s
(t,xk)+(D s+1− D s)w
s
(t,xk)− zk(t)]w
s
(t,xk)dt = 0.
Agar bu munosabatdan
c
s
(t,xk) va w
s
(t,xk) ni bilsak, keyin yaqinlashuvni
quyidagicha aniqlash mumkin.
D S+1=
∑
k=1
4
∫
0
T
[D sw
s
(t,xk)− c
s
(t,xk)+zk(t)]w
s
(t,xk)dt
∑
k=1
4
∫
0
T
w
s2(t,xk)dt
(2.49)
(2.43) tenglamani D bo’yicha differensiallaymiz va quyidagi natijani
olamiz:
∂w
∂t= D ∂2w
∂x2+λw + ∂2c
∂ x2
(2.50)
(2.44), (2.45) shartlarni D bo'yicha differensiallymiz va quyidagi natijaga
erishamiz:
w(0,x)=0
, (2.51)
w(t,0)=0
,
w(t,l)=0
. (2.52)
Bu yerda
w= ∂c
∂D -sezgirlik funktsiyasi.
D koeffitsientini topishning sonli algoritmini quyidagi ko’rinishda bo’ladi:
1) Boshidan boshlab biz
D0 dastlabki taxminiylikni beramiz (S= 0) :
2)
(t=0) dan t⊂T gacha bo‘lgan (2.43) va (2.44) masalalarni yechamiz va
c(t,x)
funksiyani aniqlaymiz, keyin (2.46) funksional qiymatni
52](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_52.png)

![j= 0,N − 1 . (2.54)
(2.49) approksimatsiyalangandan so'ng, yaqinlashuv quyidagi ko’rinishga
keladi:
D S+1=
∑
k=1
4
∑
j=0
M−1
[D Swk
j+1− ck
j+1+zk
j+1]wk
j+1
∑
k=1
4
∑
j=0
M−1
[wk
j+1]
2
.
(2.53), (2.54) ayirmali tenglamalarini quyidagi ko’rinishga keltiramiz:
Ac i−1
j+1− Cc i
j+1+Bc i+1
j+1= − F 1i
j,i= 1,N − 1,j= 0,M − 1
, (2.55)
Aw i−1
j+1− Cw i
j+1+Bw i+1
j+1= − F 2i
j,i= 1,N − 1,j= 0,M − 1
. (2.56)
Bu yerda
A= B= D Sτ
h2 ,C = 1− λτ +2 A ,F 1i
j= ci
j,F 2i
j= w i
j+ τ
h2(ci+1
j+1− 2ci
j+1+ci−1
j+1)
.
(2.55) va (2.56) masalani yechish uchun “Progonka” usulidan foydalanamiz.
ci
j+1= αi+1
(1)ci+1
j+1+βi+1
(1),i= N − 1,N − 2,...,1,0 ,cN
j+1= 0
, (2.57)
αi+1
(1)= B
C − Aα i
(1),βi+1
(1)=
Aβ i
(1)+ F 1i
j
C − Aα i
(1) ,
i= 1,N − 1,c0
j+1= α1
(!)c1
S+1+ β1
(1)= c0,α1
(1)= 0,β1
(1)= c0,
wi
j+1= αi+1
(2)wi+
j+1+βi+1
(2),i= N − 1,...,1,0 ,wN
j+1=0
, (2.58)
αi+1
(2)= B
C − Aα i
(2),βi+1
(2)=
Aβ i
(2)+ F 2i
j
C − Aβ i
(1) ,
i= 1,N − 1,α1
(2)= 0,β2
(2)= 0.
(2.59)
54](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_54.png)
![To'r x o'qi bo'yicha [0;L] segmentini 100 intervalga, [0;T] vaqt segmentini
3600 ga ajratdi. Berilgan parametrlar bilan (2.17) birinchi tenglamaning
"koordinata-vaqt" to’r yechimi asosida 5
¿ 10 nuqtada olingan:
D= 10 −6 м2/с,L= 1м ,t= 3600 c,λ= 0.0001 .
Yuqorida tahlil qilingan holatlar uchun quyidagi minimal qiymat olingan
J(D )= 0,000000001813351461609574
uchun D = 2⋅10 −6 м2/с .
D
parametrlarini identifikatsiyalash uchun hisob-kitoblar natijalari, D
0
= 10 −6
m 2
/s nolga yaqinlik sifatida qo’yilganda, (2.3-rasm) ma'lumot 2×10 nuqtada
"koordinata - vaqt" da parametr to'rtta iteratsiyada muvozanat nuqtasiga
yaqinlashadi (2.3-rasm).
55с
b)D, м 2
/с
а)](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_55.png)

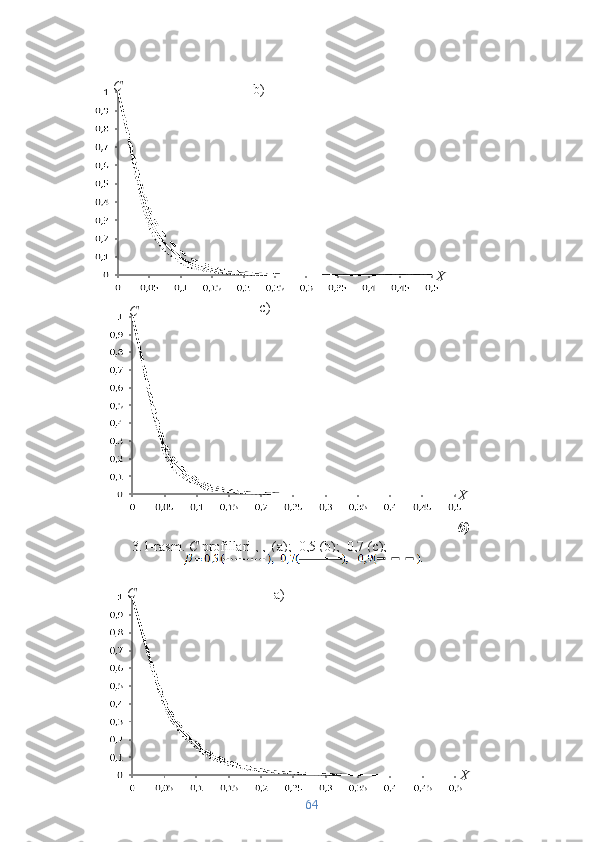
![2.3-rasm. Turli x va t =3600 c , λ= 10 −4 D = 10 −6м2/с ,x= 0,2 м (b) x= 0,35 м ;
(c);
x= 0,5 м (d) uchun profillar.
III BOB. Ikki sohali birjinslimas yoriq g’ovak muhitda anomal modda
ko’chishi teskari masalasini sonli yechish.
Ushbu bobda ikki sohali birjinslimas yoriq g’ovak muhitda anomal modda
ko’chishi teskari masalasini sonli yechish masalalarini qarab chiqqanmiz va turli
muammolarga yechim topganmiz.
Jumladan yoriq-g’ovak muhitda anomal
modda ko’chish masalasini sonli yechish masalasini 3.1- bo’limda qarab
o’tganmiz. 3.2-bo’limda esa ikki sohali bir jinslimas yoriq-g’ovak muhitda
anomal modda ko’chishining koeffitsientli teskari masalasini sonli yechish
masalasini ham qarab o’tganmiz va turli noaniqliklarga oydinlik kiritganmiz.
3.1. Yoriq-g'ovak muhitda anomal modda ko’chishi masalasini sonli
yechish.
So'nggi paytlarda suyuqlik va moddalarning bir jinsli bo'lmagan muhitda
ko’chishidagi kechikish ta'sirini tahlil qilish uchun moddalarni filtrlash va
ko’chish tenglamalarida vaqt va fazoda o'zgaruvchan kasr hosilalarni hisobga
oladigan yondashuv qo'llanildi [19,38].
57](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_57.png)
![Bu yerda yaxshi o'tkazuvchan (tranzit) va yomon o'tkazuvchan turg'un
zonalardan tashkil topgan bir xil bo'lmagan g'ovak muhit ko'rib chiqiladi, bu
yerda tranzit zonada moddalarning izotermik bo'lmagan o'tish jarayoni sodir
bo'ladi va hosil bo'lgan konsentratsiya gradientlari tufayli zonalar o'rtasida
massa almashinuvi sodir bo'ladi. U o’tkazuvchan bo’lganda modda atrof-
muhitga tarqalishi mumkin. Turg'un zonaning geometrik xususiyatlarini
ko'rsatmasdan, zonalar orasidagi massa almashinuvi, shuningdek, materiyani
uzatish uchun tenglamada materiyaning diffuziya oqimi, vaqtga nisbatan
materiya kontsentratsiyasining kasr hosilasi sifatida manba atamasi bilan
modellashtirilgan. Bu moddani ko’chish jarayonida anomal hodisalarni hisobga
olish imkonini beradi. E'tibor bering, anomal hodisalarni hisobga olmagan holda
zonalarning geometrik xarakteristikalarini ko'rsatmaslik va bunday muhitlarda
moddalar ko’chishning ba'zi muammolari ko'rib chiqilgan.
Tuzilgan shartlarga muvofiq, bir o'lchovli holatda moddaning ko’chishi
quyidagi tenglama bilan ifodalash mumkin [43].
58](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_58.png)
![m ∂с
∂t+v∂c
∂x+a2
∂γc
∂tγ+a3
∂βc
∂tβ= ∂
∂x(mJ ), (3.1 )
J= D (p ∂αc
∂xα+(1− p) ∂αc
∂(− x)α)
, (3.2)
bu yerda
с ‒ moddaning hajmiy konsentratsiyasi, t vaqt, ‒ J - nisbiy diffuziya
massa oqimi
м/с , m - ko’chish zonasining g'ovakliligi, D - effektiv diffuziya
koeffitsienti,
м1+α/с , a3 - moddaning atrof-muhitga o'tishi bilan bog'liq
retartatsiya koeffitsienti,
сβ−1 , a2 ‒ ikki zona o'rtasidagi massa o'tkazuvchanligi
bilan bog'liq retartatsiya omili,
сγ−1 , v - filtrlash tezligi м/с , α,β,γ− hosilalar
tartibi
(0<α≤ 1, 0< β<1, 0,5 ≤ γ≤ 1) , p(0≤ p≤ 1) markaziy simmetriyadan
hosil bo’lgan va orqada qolgan dispersiyaning nisbatini tavsiflaydi. Agar
p<1
2 ,
dispersiya sekin shakllanishi bilan simmetriyadan orqada qoladigan xarakterga
ega. Agar
p>1
2 dispersiya tez shakllanishi bilan simmetriya nisbatan oldinda
bo’ladi [12] .
Yarim cheksiz g'ovak muhit
с0 hajmiy konsentratsiyali suyuqlik bilan
to'ldirilsin,
t>0 momentidan boshlab unga с1 moddaning hajmli
konsentratsiyasi bo'lgan suyuqlik oqib chiqa boshlaydi. Cheksizlikda asl
konsentratsiya
с0 saqlanib qoladi. Keyin boshlang'ich va chegaraviy shartlar
quyidagi shaklda qo’yiladi
c(0,x)= c0, 0≤ x<∞ ,
(3.3)
c(t,0)=c1,c(t,∞ )= c0.
(3.4)
59](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_59.png)

![∂C
∂¯t+V ∂C
∂X +b2
∂γC
∂¯tγ+b3
∂βC
∂¯tβ= 1
Pe
∂2C
∂X 2. (3.9)
(3.9), (3.7), (3.8) masalani yechish uchun chekli ayirmalar usulidan
foydalanamiz. Jarayon o'rganiladigan
tmax maksimal vaqt bo'lgan holda
D = {0≤ X <∞ ,0≤ ¯t≤ tmax }
sohada biz h qadam va τ vaqt bo'yicha to’r
kiritamiz. Natijada quyidagi to’rga ega bo’lamiz:
ωhτ= {(Xi,¯tj),i= 0,1,2 ,..., j= 0,1 ,...,J; Xi= ih ; ¯tj= jτ ; τ= T/K }.
(3. 9 ) tenglamani oshkormas ayirmalar sxemasidan foydalangan holda
ωhτ
to'rda approksimatsiyalaymiz .
C
i
j+1
−C
i
j
τ
+V
C
i
j+1
−C
i−1
j+1
h
+
b
2
τ
1−γ
Γ(2− γ)
¿[
∑
k=0
j−1
C
i
k+1
−C
i
k
τ
((j− k+1)
1−γ
−(j−k)
1−γ
)+¿
]
¿
¿
¿
¿
¿
(3
.10)
Boshlang'ich va chegaraviy shartlar quyidagicha qo’yiladi
С i
0= С 0, i= 0,1 ,...
I , (3.11)
C0
j= С1, C I
j= С0, j= 0,1 ,...J,
(3.12)
bu yerda
I - (3.12) shart taxminan qanoatlantiriladigan yetarlicha katta son.
(3.10) ayirmali sxemasi quyidagi chiziqli tenglamalar sistemasiga
keltiriladi
AС i−1
j+1− BС i
j+1+EС i+1
j+1= − Fi
j
, i=1,I−1 , j=0,J , (3.13)
61](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_61.png)
![bu yerdaA= − Vτ
h − τ
Peh 2
,
B=− 1− Vτ
h −
b2τ1−γ
Γ (2− γ)
−
b3τ1−β
Γ (2− β)
− 2τ
Peh 2
,
E=− τ
Peh 2
,
Fi
j=(−1−
b2τ1−γ
Γ(2− γ)
−
b3τ1−β
Γ(2− β)
)Сi
j+
b2τ1−γ
Γ(2− γ)
¿[∑
k=0
j−1
((j−k+1)1−γ−(j− k)1−γ)Сi
k+1− ¿
]
¿
¿
¿
¿
¿
(3.13) sistema ma'lum
Сi
j uchun progonka usuli bilan yechiladi.
Hisoblashda dastlabki parametrlarning quyidagi qiymatlari ishlatilgan:
С0= 0
, С1=1 , V= 0,01 , Pe = 10 4 va har xil β,γ,b2,b3 .
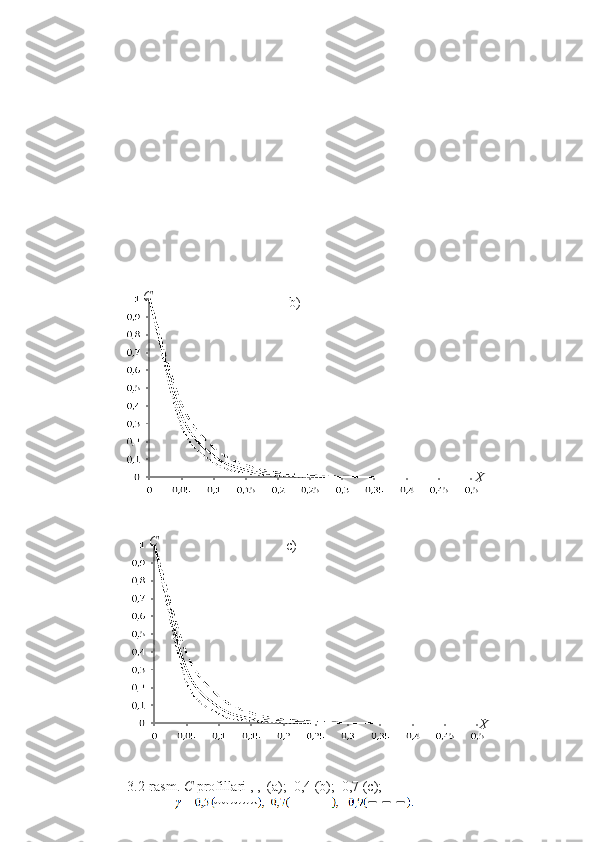
Ba'zi natijalar 3.1 3.3-rasmlarda ko'rsatilgan. Natijalardan ko'rinib
‒
turibdiki,
β ko'rsatkichning birdan kamayishi profillarni ishlab chiqishda
kechikishga olib keladi (3.1a-rasm).
b2≠ 0 da kuzatiladigan tranzit va turg'un
zonalar orasidagi massa o'tkazmasini hisobga olish, profillarni ishlab chiqishda
yanada katta kechikishga olib keladi (3.1b-rasm). Shuni ta'kidlash kerakki,
moddaning atrof-muhitda ko’chishi va zonalar orasidagi massa almashinuvi
hisobga olinsa,
β parametrning ta'siri zaiflashadi. 3.1a-rasmda β
kontsentratsiya profillariga ta'siri 3.1b-rasmga qaraganda sezilarliroqdir.
62](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_62.png)



![3.2. Yoriq-g’ovak muhitlarda modda ko’chishining koeffitsientli
teskari masalasini sonli yechish.
Moddalarning yaxshi o'tkazuvchan (tranzit) va yomon o'tkazuvchan
(turg'un) sohalardan tashkil topgan bir jinsli bo'lmagan g'ovakli muhitda
ko’chishi, sohalarda muvozanatsiz adsorbsiyani hisobga olgan holda ko'rib
chiqamiz. Ko’chish sohasida ikkita muhit mavjud bo'lib, ularning har birida
qaytariluvhchan muvozanat kinetikasiga ega bo'lgan moddaning adsorbsiyasi
sodir bo'ladi. Ikkinchi soha bilan moddaning almashinuvi manba hadsi bilan
birinchi sohadagi moddaning kontsentratsiyasi vaqtiga nisbatan kasr hosilasi
sifatida modellashtirilgan. Ushbu yondashuv natijalari ma'lum, an'anaviy
yondashuvlar bilan taqqoslanadi. Jarayonni modellashtirishning bu usuli yaxshi
natija berishi ko'rsatilgan. Manba hadsi parametrlarini to'g'ri tanlash orqali
bikontiniual yondashuvga yaqin natijalarga erishish mumkin.
Yaxshi o'tkazuvchan (tranzit) va yomon o'tkazuvchan turg'un sohalardan
tashkil topgan bir hil bo'lmagan g'ovakli muhit ko'rib chiqiladi, uning sxemasi 1-
rasmda ko'rsatilgan. Birinchi zonadagi parametrlar 1 indeksi bilan belgilanadi.
Soha ikkita bo'limga ega bo'lib, ularning har biri qaytariladigan muvozanatsiz
kinetikaga ega bo'lgan moddani cho'ktiradi. Moddalar almashinuvi ikkinchi soha
bilan sodir bo'ladi, biz birinchi sohadagi moddaning kontsentratsiyasi vaqtiga
nisbatan kasr hosilasi sifatida modellashtiramiz. Shuning uchun, [11] dan farqli
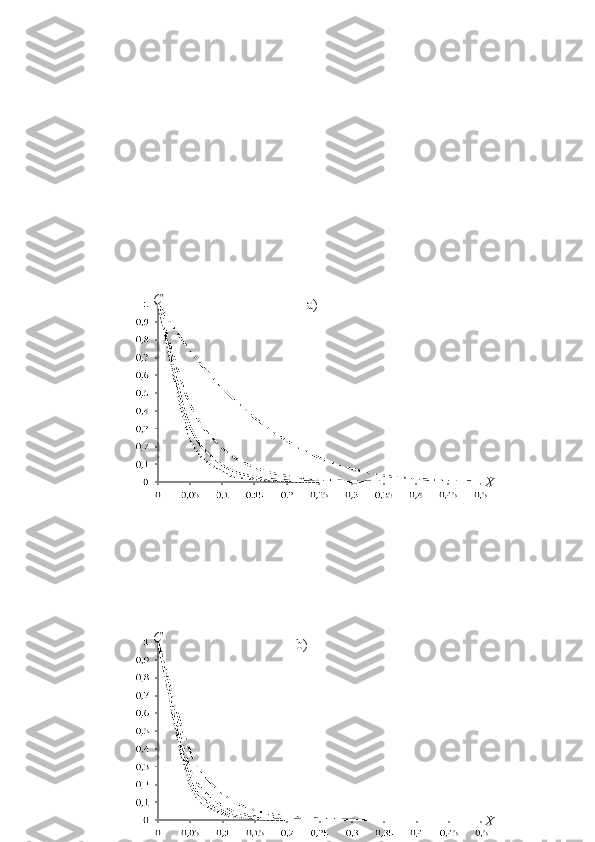
693.3 -rasm . С profillari , а)
b)
c)](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_69.png)
![o'laroq, ikkinchi zonadagi konsentratsiya maydoni hisobga olinmaydi. Esda
tutingki, kasr yondashuvi ilgari [34] da qo'llanilgan.
2. Matematik model va uning sonli amalga oshirilishi
Bir o'lchovli holatda modda ko’chishi tenglamasini quydagi shaklda
yoziladiρ ∂ S a1
∂ t + ρ ∂ S s1
∂ t + θ1
∂ C 1
∂ t + a2
∂γC 1
∂ tγ = θ1D 1
∂2C 1
∂ x2 − θ1v1
∂ C 1
∂ x ,(3 .14 )
bu yerda
t vaqt, s, x - masofa, m, D1 bo'ylama dispersiya koeffitsienti ,
m2/s
, v1
suyuqlikning tezligi, m/s , С1 suyuqlikdagi moddaning hajm
konsentratsiyasi
Sa1 va Ss1 yotqizilgan kontsentratsiyalar . modda, m3/kg , θ1 -
g'ovaklik,
m3/m3 , ρ - muhitning zichligi, kg /m3 , a2 - moddaning ikkinchi
muhitga o'tishidagi kechikish omili,
sγ−1 .
70 Ikkinchi zonabirinchi zona
1-rasm. Ikki zonali moddalarni uzatish sxemasi](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_70.png)

![chiqilayotgan maydonda Ω= {(t,x),0≤t≤T ,0≤ x≤∞}
yo'nalishlarda grid
formasini joriy qildi
ωτh= ¿{(tj,xi);tj=τj , xi= ih ,τ=
T
J
,¿}¿{}
,
bu yerda I - yetarlicha katta butun son bo'lib,
[0,xI], segmentda bo'lishi
uchun tanlangan,
xi=ih,
C
1 , S
a1 va S
s1 maydonlarida hisoblangan o'zgarish
maydonini bir-birining ustiga qo'ydi , h- x yo'nalishidagi to’r qadamidir .
Ochiq to’r maydonida
ωτh=¿{(tj,xi);tj=τj,xi=ih,τ=
T
J
,¿}¿{}
(1), (2), (3) tenglamalar quyidagicha approksimatsiya qilingan
72](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_72.png)

![(Ss1)i
j+1= qb1(Ss1)i
j+qb2, (3.24)
bu yerda,
pb1= 1
1+τk ad 1
,
pb2=
τθ 1ka1
ρ+ρτ kad 1
(C1)i
j,
qb1= 1
1+τk sd 1
,
qb2=
τθ 1ks1
ρ+ρτ ksd1
(C1)i
j .
Grid tenglamalari (7) shaklga keltiriladi
− A1(C 1)i−1
j+1+B1(C1)i
j+1− E1(C1)i+1
j+1=(F1)i
j,
(3.25)
bu yerda
A1=
θ1D1τ
h2 +
θ1v1τ
h
,
B1=θ1+2θ1D1τ
h2 +θ1v1τ
h + a2τ1−γ
Γ(2−γ)
E1=
θ1D1τ
h2
,
(F1)i
j=(θ1+
a2τ1−γ
Γ(2−β)
)(C1)i
j−ρ((Sa1)i
j+1−
−(Sa1)i
j)−ρ((Ss1)i
j+1−(Ss1)i
j)−
−
a2
Γ(2−γ)
¿
[∑
k=0
j−1
((j−k+1)1−γ−(j−k)1−γ)(С1)i
k+1−¿]¿
¿
¿¿
Yechimni hisoblashning quyidagi tartibi o'rnatiladi. (3.23), (3.24) ga ko'ra,
(Sa1)i
j+1
, (Ss1)i
j+1 aniqlanadi, so'ngra (C1)ij+1− chiziqli tenglamalar tizimini (3.25)
progonka usuli bilan yechamiz.
Chunki
pb1,qb1<1 (3.23), (3.24) sxemalar
barqaror va (12) uchun progonka usulining barqarorlik shartlari bajariladi.
74](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_74.png)
![Taklif etilayotgan modelning samaradorligini baholash uchun natijalarni
tegishli natijalar bilan taqqoslash muhimdir [11]. Buning uchun [4] va a2
∂γC1
∂tγ
( 3.14 ) dagi cho'kish shartlarini taqqoslay miz.
α(С2−С1)
Egri chiziqlar asosida
natijalarning yaqinligini aniqlash uchun biz hisoblab chiqdik
δ1=∫
0
L
(I1−I2)2dx
(3.26)
t ning berilgan qiymati uchun , bu yerda L kontsentratsiya profillari
cho'zilgan hududning shartli chegarasi;
I1= α(C 2− C 1), I2= a2
∂γC 1
∂tγ .
Oqim muddatlarining yaqinligi
I1va I2 tavsiya etilgan yondashuv va model
yordamida aniqlangan kontsentratsiya maydonlarining yaqinligini kafolatlashi
kerak [11].
С1, Ularning yaqinligini baholash uchun biz (3.26) o'rtacha
kvadratik chetlanishdan foydalanamiz, faqat
С1, uchun ikki modelga asoslangan
holda, ya'ni,
δ2=∫
0
L
(C1
(1)−C1
(2))
2dx ,
bu yerda
C1(1) [11] ga muvofiq aniqlangan, berilgan t dagi C1(t,x)
konsentratsiya maydoni
C1(2)−
bu yerdagi belgilangan bilan bir xil.
Boshqa lahzalar uchun
tva α,а2,γ
mutlaqo boshqa baholarni olish
mumkin. Asosiy holda , ikkita modelni taxmin qilish
δ1и δ2. uchun ma'lum bir
qiymat uchun
α ta'riflar bo'yicha tegishli koeffitsientli teskari masalalarni
qo'yish va hal qilish kerak
а2,γ yoki aksincha, α berilgan а2 va γ.
75](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_75.png)
![Hisoblashda dastlabki parametrlarning quyidagi qiymatlari ishlatilgan:c0=0,
v1=10 −4m/s , D1=v1⋅αl αl=0,005 м, ρ=1800 kg /m3 θ1=0,1 ,
ka1=3⋅10 −4s−1,kad1= 2,5 ⋅10 −4s−1,
ks1=4⋅10 −4s−1, ksd1= 2⋅10 −4s−1 va har xil
a2,γ.
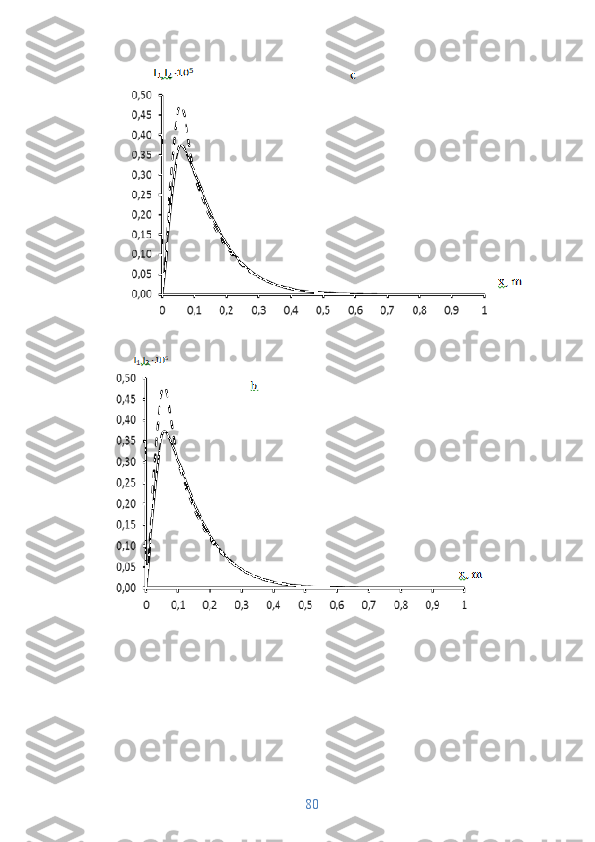
Ba'zi hisoblash natijalari shaklda ko'rsatilgan. 2-rasmdan ko'rinib turibdiki,
moddaning ikkinchi zonaga chiqishi mobil suyuqlikdagi moddaning
konsentratsiya profillarining kechiktirilgan tarqalishiga olib keladi. Ushbu
hodisa natijasida adsorbsiyalangan moddaning kontsentratsiyasida ham
kechikishlar kuzatiladi.
Muayyan parametrlar to'plami uchun
a2,γи α=10 −4с−1 grafiklar I1, I2
3-
rasmda ko'rsatilgan. Rasmdan ko'rinib turibdiki, cho'kish shartlarini o'zgartirish
naqshlari o'xshashdir, bu taklif qilingan model natijalari va model natijalari
o'rtasidagi sifat kelishuvini ko'rsatadi [4].
Endi biz funksiyani minimallashtiramiz
Ф(a2,γ)=∫
0
T
∫
0
L
(I1− I2)2dx dt
(3.27)
Qiymatlar
Ф(a2,γ) butun vaqt davri uchun standart og'ishni tavsiflaydi .
I1от I2
Amalga oshirilgan hisob-kitoblar minimal qiymatga Ф(a2,γ)
erishilganligini ko'rsatadi
a2=0,0006 ,γ=0,8 .
Oqim muddatlarining yaqinligi
I1и I2 tavsiya etilgan yondashuv va [11]
model yordamida aniqlangan kontsentratsiya maydonlarining yaqinligini
kafolatlashi kerak. Buning uchun
С1 mos keladigan profillar qurilgan (4-rasm).
Grafiklardan ko'rinib turibdiki, yechimlar bir-biriga yaqin. Ularning yaqinligini
sonli baholash uchun biz (3.27) turdagi standart
С1, og'ishdan foydalanamiz,
buning uchun faqat ikkita model asosida aniqlanadi, ya’ni
76](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_76.png)
![F(a2,γ)=∫
0
T
∫
0
L
(C1
(1)−C1
(2))
2dxdt ,bu yerda
C1(1)− berilgan t dagi C1(t,x)
konsentratsiya maydoni, [11] ga
muvofiq aniqlanadi va
C1(2)− bu yerda bir xil bo'ladi. Yuqorida tahlil qilingan
holatlar uchun quyidagi minimal qiymat olingan
F(a2,γ)= 0,002347387654452 uchun а2=0,0006 ,γ=0,8 .
77](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_77.png)


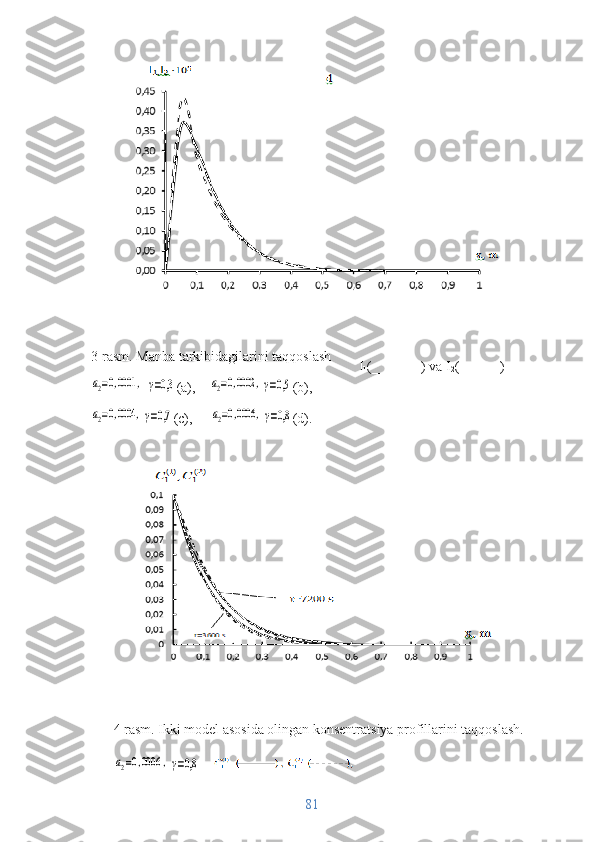
![Yuqoridagi 3.2 paragrifdagi bir jinislimas g’ovak muhitda modda ko’chishi
tenglamasidagi a
2 va D koeffisentni topish masalasini bu 3.2 paragrifda ko’rib
chiqamiz. Bunda biz 3.2 paragrifdagi tenglamlardan, shartlar va
approksimasiyadan foydalanamiz.
Endi biz funksiyani minimallashtiramizФ(a2,D)=∫
0
T
∫
0
L
(I1− I2)2dx dt
(3.28)
Qiymatlar
Ф(a2,D) butun vaqt davri uchun standart og'ishni tavsiflaydi .
I1от I2
Amalga oshirilgan hisob-kitoblar minimal qiymatga Ф(a2,D)
erishilganligini ko'rsatadi
a2=0,0006 ,D=10 −6.
Oqim muddatlarining yaqinligi
I1и I2 tavsiya etilgan yondashuv va [4]
model yordamida aniqlangan kontsentratsiya maydonlarining yaqinligini
kafolatlashi kerak. Ularning yaqinligini
sonli baholash uchun biz (14) turdagi standart
С1, og'ishdan foydalanamiz,
buning uchun faqat ikkita model asosida aniqlanadi, ya’ni
F(a2,γ)=∫
0
T
∫
0
L
(C1
(1)−C1
(2))
2dxdt ,
bu yerda
C1(1)− berilgan t dagi C1(t,x)
konsentratsiya maydoni, [11] ga
muvofiq aniqlanadi va
C1(2)− bu yerda bir xil bo'ladi. Yuqorida tahlil qilingan
holatlar uchun quyidagi minimal qiymat olingan
F(a2,D)= 0,002347387654452 uchun а2=0,0006 ,D=10 −6.
82](/data/documents/f91cc645-b808-412b-a3a8-24d61bb0ccfc/page_82.png)


















YORIQ-G’OVAK MUHITLARDA ANOMAL MODDA KO’CHISHI TESKARI MASALASINI SONLI YECHISH MUNDARIJA Kirish …………………………………………………………...……………….3 I BOB. Matematik fizikaning teskari masalalari va yoriq-g'ovak muhitda anomal modda ko’chishi jarayonining matematik modellari .........................6 1.1. Matematik fizikaning teskari masalalarini tasniflash ............................. ........6 1.2. Yoriq-g'ovak muhitda anomal modda ko’chishining matematik modellari..............................................................................................................18 1.3. Yoriq-g'ovak muhitda anomal modda ko’chishi jarayonlarini modellashtirish....................................................................................................28 II BOB. G ’ ovak muhitda anomal modda ko’chishi bir o’lchovli masalasini sonli yechish .......................................................................................................34 2.1. Yoriq-g'ovak muhitda anomal modda ko’chishda kasr hosilalar va ularni hisoblash. ……………....................................................................... ..................34 2.2. G’ovak muhitda anomal modda ko’chish masalasini yechish......................45 2.3. G'ovakli muhitda anomal modda ko’chishning bir o'lchovli teskari masalasini sonli yechish ........................................................................................................49 III BOB. Ikki sohali birjinslimas yoriq g’ovak muhitda anomal modda ko’chishi teskari masalasini sonli yechish .......................................................56 3.1. Yoriq-g'ovak muhitda anomal modda ko’chishi masalasini sonli yechish..56 3.2. Ikki sohali birjinslimas yoriq- g'ovak muhitda anomal modda ko’chishining koeffitsientli teskari masalasini sonli yechish..............................67 1
Xulosa ………………………………………....……………………................79 Foydalanilgan adabiyotlar …………………………....……………................81 Ilovalar ................................................................................................................92 2
KIRISH Dissertasiya mavzusining dolzarbligi va zarurati: Jahon miqyosida neft qazib olish sanoatida neft qatlamlariga ikkilamchi va uchlamchi usullari bilan ta’sir etishning takomillashgan loyihasini ishlab chiqish yetakchi o’rinni egallamoqda. So’ngi yillarda ko’pgina rivojlangan mamlakatlarda neftni qazib olish sanoatida, g’ovak muhitlarda modda ko’chishi jarayonini ifodalovchi klassik modellar o’rniga moddaning anomal ko’chishi jarayonini ifodalovchi noklassik modellar qo’llanilmoqda. Bu borada, jumladan AQSh, Rossiya, Xitoy va boshqa rivojlangan davlatlarning ne ft va gazni qazib olish sanoatlarida, neft qatlamlaridagi g’ovak muhitlarda birjinslimas suyuqliklar sizishi va moddaning anomal ko’chishi jarayonlariga ta’sir etuvchi asosiy omillarni hisobga olgan holda loyihalash usullarini takomillashtirishga alohida e’tibor qaratilgan. Birjinslimas g'ovak muhitlarda modda ko’chishining to'g'ri masalalari turli hollar uchun yechilgan. Lekin teskari masalalar faqat ayrim sodda hollar uchun yechilgan. Juda muhim masalalar hozirgacha yechilmagan. Mavzu ana shunday masalalarni sonli yechishga bag'ishlangan. Shuning uchun masalalar va umuman mavzu dolzarb hisoblanadi. Muammoning o’rganilganlik darajasi. Bir jinslimas yoriq- g’ovak muhitlarda modda ning ko’chishi hamda har xil xarakteristikalarga ega bo’lgan ikki sohali muhitda modda ko’chishi masalalarini A.Suzuki, A.S.Fomin, V.A.Chugunov, T.Hashida, Y.Nibori, A.S.Bredford, F.J.Leij, H.Makita, J.Simunek, N.Toride, S.E.Silliman va boshqa olimlar tomonidan ilmiy tadqiqotlar olib borilgan. Birjinslimas yoriq g’ovak muhitlarda moddaning ko’chishi masalalari bo’yicha taniqli olim va tadqiqotchilardan A.D.Benson, M.M.Meerschaert, W.S.Wheatcraft, F.Huang, F.Liu, M.Sahimi, R.Schumer, B.Baeumer, N.R.Horne, H.Zhan, B.F.A.Tompson, J.Akilov, B.X.Xo’jayorov, V.F.Burnashev 3
va boshqalar tomonidan izlanishlar olib borilgan va ma’lum darajada ijobiy natijalarga erishilgan. Bugungi kunda yoriq g’ovak muhitlarda modda ko’chishi teskari masalalari to’liq o’rganilmagan. Tadqiqotning maqsadi yoriq-g’ovak muhitlarda moddaning ko’chishining teskari masalasini sonli yechish va tahlil qilishdan iborat. Tadqiqotning vazifalari: To’gri va teskari masalalarni qo’yilishini matematik modellarini tahlil qilish; g’ovak muhitlarda modda ko’chishining matematik modellarini sonli yechish; yoriq- g’ovak muhitlarda anomal modda ko’chishining matematik modellarini sonli yechish ; ikki sohali bir jinslimas yoriq g’ovak muhitda modda ko’chishini teskari masalasi sonli yechish. Tadqiqotning obyekti sifatida birjinslimas suyuqliklar yoriq-g’ovak muhitlarda modda ko’chishi modeli olingan. Tadqiqotning predmeti yoriq-g’ovak muhitlarda moddaning ko’chishi jarayonining matematik modellari, hisoblash algoritmlari va kompyuterda sonli tajribalar o’tkazish uchun dasturiy majmualari va gidrodinamik tahlil jarayonlarini tashkil etadi. Tadqiqotning ilmiy yangiligi. To’gri va teskari masalalarni qo’yilishini matematik modellarini tahlil qilindi; g’ovak muhitlarda modda ko’chishining matematik modellarini sonli yechildi ; yoriq- g’ovak muhitlarda anomal modda ko’chishining matematik modellarini sonli yechildi ; 4
ikki sohali bir jinslimas yoriq g’ovak muhitda modda ko’chishini teskari masalasi sonli yechildi. Tadqiqotning amaliy natijalari quyidagilardan iborat: differensial tenglamalar asosida moddaning ko’chishi jarayonining matematik modeli, hisoblash algoritmlari ishlab chiqilgan; yoriq-g’ovak muhitlarda nomuvozanat adsorbsiyali modda ko’chish jarayonini hisoblash uchun dasturiy vosita ishlab chiqilgan; ikki sohali yoriq g’ovak muhitda kinetika asosida modda ko’chishining teskari masalasi uchun dasturiy vosita ishlab chiqilgan. Tadqiqotning tuzilmasi. Magistrlik dissertatsiyasi mavzusi, kirish, uch bob, xulosa, foydalanilgan adabiyotlar ro’yxati va ilovalardan iborat. Dissertatsiya mavzusi bo’yicha chop etilgan ilmiy ishlar. 1) Ешдавлатов З, Тўрайев Ф, Холиқов Ж. A номальный перенос растворенных веществ в елементе трещиновато-пористой среды. 2022-йил 18-19 ноябр ь . 2) Dzhiyanov T.O.1, Xolikov J.R.2, Abduraxmonov M.S.3. Solute transport in a two-zone medium with kinetics. 1,2,3Samarkand State University, Samarkand, Uzbekistan. 3) Numerical Solution of the Inverse Problem of Solute Transport in Non-Homogeneous Porous Media. Dzhiyanov T.O., Xoliqov J. 5
