DETERMINANTLAR VA ULARNING XOSSALARI












![Δ=|
a11 a12 a13 a14
a21 a22 a23 a24
a31 a32 a33 a34
a41 a42 a43 a44
|=
= a11|
a22 a23 a24
a32 a33 a34
a42 a43 a44
|− a12|
a21 a23 a24
a31 a33 a34
a41 a43 a44
|+a13|
a21 a22 a24
a31 a32 a34
a41 a42 a44
|− a14|
a21 a22 a23
a31 a32 a33
a41 a42 a43
|.Bundan yuqori tartibli determinantlarning ham kattaligi yuqoridagiga
o‘xshash hisoblanadi. Masalan, 6-tartibli determinantning kattaligini hisoblash
kerak bo‘lsa, uni biror satri yoki ustuni elementlari bo‘yicha yoyib 5-tartibli
determinantlarga, keyin o‘z navbatida 5-tartibli determinanatlarni ham biror satri
yoki ustuni elementlari bo‘yicha yoyib, 4-tartibli determinantlarga keltiriladi va
hokazo.
Determinantlarning yuqorida ko‘rsatilgan xossalari hamma tartibli
determinantlar uchun ham to‘g‘ri. Endi yuqori tartibli determinantlarni
hisoblashga misol qaraymiz. Ushbu determinantning kattaligini hisoblang.
|
2 0 3 0
− 1 3 2 4
− 2 4 0 3
0 2 1 1
|
Yechish. Berilgan determinantni 1-satr elementlari bo‘yicha yoyib
hisoblaymiz:
|
2 0 3 0
− 1 3 2 4
− 2 4 0 3
0 2 1 1
|= 2⋅|
3 2 4
4 0 3
2 1 1
|− 0⋅|
− 1 2 4
− 2 0 3
0 1 1
|+3⋅|
− 1 3 4
− 2 4 3
0 2 1
|− 0⋅|
− 1 3 2
− 2 4 0
0 2 1
|=
2[3⋅|0 3
1 1
|− 2⋅|4 3
2 1
|+4⋅|4 0
2 1
|] +3⋅[(− 1)⋅|4 3
2 1
|− 3⋅|− 2 3
0 1
|+4⋅|− 2 4
0 2
|]=
= 2(− 9+4+16 )+3(2+6− 16 )= 22 − 24 = − 2.](/data/documents/cdaefa92-6c34-4d95-9718-f67f0a0927c9/page_14.png)



DETERMINANTLAR VA ULARNING XOSSALARI Reja 1. Algebra va uning rivojlanish tarixidan. 2. 2, 3-tartibli determinantlar. 3. Determinantlarning xossalari. 4. Minor va algebraik to‘ldiruvchilar. 5. n - tartibli determinantlar.
1.Algebra va uning rivojlanish tarixidan. Algebra matematikaning bir qismi va u turli miqdorlar ustida amallarni hamda shu amallar bilan bog‘liq tenglamalarni yechishni o‘rganadi. Kengroq ma’noda algebrada ixtiyoriy tabiatli to‘plamning elementlari ustida sonlarni qo‘shish va ko‘paytirish kabi odatdagi amallarni umumlashtiruvchi amallarni o‘rganuvchi fan tushuniladi. Uch og‘aynning yoshlari 30, 20, 6 da. Necha yildan keyin eng kattasining, yoshi ikkala qolgan yoshlarining yig‘indisiga teng bo‘ladi.30 +x=(20 +x)+(6+x), x=4. Bunday tenglamalar eramizdan avval 2 minginchi yillarda qadimgi Misrda ma’lum edi. Lekin ular harflardan foydalanmagan. Eramizdan avvalgi 2 minginchi yil boshida qadimgi bobilliklar yanada murakkabroq masalalarni yechishgan. III asrda yashagan iskandariyalik olim Diofant geometrik bayonni rad etib harfiy ifodalardan foydalanadi. Unda manfiy ko‘rsatkichli darajalar, manfiy sonlar, musbat va manfiy sonlarni ko‘paytirish qoidalarini yozish uchun qisqacha belgilar bor edi. Algebraning keyingi rivojiga Diofant o‘rgangan algebraik tenglamalar kuchli ta’sir ko‘rsatgan. VI asrdan boshlab matematik tadqiqotlar markazi Hindiston, Xitoy, Yaqin Sharq va O‘rta Osiyo mamlakatlariga ko‘chdi. Xitoylik olimlar chiziqli tenglamalar sistemasining yechimini topishda noma’lumlarni ketma-ket yo‘qotish usulini topishgandi. Ammo algebra, tenglamalarni yechish masalalariga bog‘liq muammolarni bayon etuvchi matematikaning maxsus tarmog‘i Yaqin Sharq va O‘rta Osiyo olimlari ishlarida shakllandi. IX asrda o‘zbek matematigi va astranomi Muhammad ibn Muso al Xorazmiy (783-850) «Al-jabr val muqobala» asarini yozdi. Bu asarda Xorazmiy chiziqli tenglamalarni yechishning umumiy qoidasini berdi va kvadrat tenglamalarni sinflarga ajratib, har bir sinf uchun yechish yo‘llarini ko‘rsatdi. Al-jabr (tiklash) so‘zi tenglamadagi manfiy hadlarni uning ikkinchi qismiga ishorasini o‘zgartirib o‘tkazishni bildirgan. Yangi fan « Algebra » ni ng n omi o‘sha «Al-jabr» so‘zidan olingan.
Qisqacha, al-Xorazmiy to‘g‘risida ma’lumotlarni qaraganda Xorazmiy o‘qish, yozish va sanashni mahalliy diniy maktab, madrasada oldi. U ilmiy masalalarni o‘z o‘qituvchilaridan yaxshiroq tushunar, juda ko‘p o‘qir, o‘z ustida tinimsiz ishlar, madrasaning majburiy darsliklari bilan chegaralanib qolmas edi. Xorazmiyning yoshlik davri Xorazmni arablar zabt etgan davrga to‘g‘ri keladi. Beruniyning yozishicha, arab istilochilari Xorazmning milliy madaniyatini yo‘q qilib yuborgani, kitoblarning kuydirilganini, olimlarni o‘zlari bilan olib ketganini, bo‘ysunmaganlarini o‘ldirganini yozadi. Shu sabab bo‘lsa kerak, VIII asr oxirida Xorazmiy Bag‘dodga keladi. Bu asr o‘rtalarida davlat boshiga abbosiylar kelgan va Sharqiy arab xalifaligida hayot o‘z iziga tusha boshlagan edi. Bag‘dodda turli kasb egalari, olimlar to‘plana boshlaydi. Fanning rivojlanishi Xorun ar-Rashid (786-809) va uning o‘g‘li Al-Ma’mun xalifalik qilgan (813-833) davrga to‘g‘ri keladi. Al-Ma’mun Bag‘dodda «Bayt al-hikmat» (Donishmandlar uyi)ni qurdiradi. Bunda yaxshi rasadxona, boy kutubxona bor edi. Uni o‘z davrining Akademiyasi desa bo‘lar edi. Xorazmiy Bag‘dodga kelib ilmiy ishlar bilan shug‘ullanadi. Tez orada Xorazmiy matematika, astronomiya, geografiya, tarix va tabobat ilmi bo‘yicha butun O‘rta Sharqda shuhrat qozondi. U «Donishmandlar uyi»da ilmiy ishlarga, kutubxonaga, rasadxonaga rahbarlik qildi. Uni Fanlar Akademiyasining birinchi prezidenti deyish mumkin. Xorazmiyning matematikaga qo‘shgan hissasi beqiyos. Uning «Hind hisobi» nomli asari o‘nli sistema raqamlari 0, 1, 2, . . . , 9 ga bag‘ishlangan. Ularni soddalashtiradi va birinchi marta arab tilida bayon etadi. Bu raqamlar Xorazmiy asari orqali arablarga, keyin Yevropaga o‘tadi. Matematikadagi algoritm termini ham Xorazmiyning nomi bilan bog‘liq, Al-Xorazmiy lotincha al-goritm deyilgan va shu so‘zdan kelib chiqqan. Xorazmiy o‘rta asr Sharqida yaratilgan birinchi matematik-astronomik jadvallarning muallifi. Amerikalik sharqshunos olim Sorton Xorazmiyni «barcha zamonlarning eng buyuk matematiklaridan biridir» deb ta’riflaydi.
2. 2, 3 - tartibli determinantlar. Determinantlarni hisoblashga keltiriladigan ushbu masalani qaraylik. Masala.A va B mahsulotlarni ishlab chiqarish uchun 2 turdagi xom ashyodan foydalaniladi. Bitta A mahsulotni ishlab chiqarish uchun 5 birlik, 1-tur va 4 birlik 2-tur xom ashyo sarflanadi,bitta B mahsulotni ishlab chiqarish uchun esa, 3 birlik, 1-tur va 5 birlik 2-tur xom ashyo ishlatiladi. 1-tur xom ashyo 62 birlik, 2-tur xom ashyo 73 birlikda berilgan bo‘lsa, eng katta foyda olinadigan ishlab chiqarishni rejalashtirish uchun xom ashyo sarfi modelini tuzing. Bu masalaning matematik modelini tuzish maqsadida x1 bilan ishlab chiqarilishi kerak bo‘lgan A mahsulot miqdorini, x2 bilan esa ishlab chiqarilishi kerak bo‘lgan B mahsulot miqdorini belgilaylik. Bu holda 5x1 A mahsulotni ishlab chiqarish uchun sarflangan 1-tur xom ashyo miqdorini, 3x2 esa B mahsulotni ishlab chiqarish uchun sarflangan 1-tur xom ashyo miqdorini ifodalaydi. 5x1+3x2 A va B mahsulotlarni ishlab chiqarish uchun sarflanadigan 1-tur xom ashyo jami sarfi miqdorini ifodalaydi, bu xom ashyo chegaralangan bo‘lib, 62 birlikda mavjud, demak 5 x1+3 x2= 62 tenglama kelib chiqadi. Xuddi shunday qilib, 2-tur xom ashyo sarfi uchun 4 x1+ 5 x2= 73 tenglamani hosil qilish mumkin. Shunday qilib, { 5x1+3x2= 62 , 4x1+5x2= 73 ikki noma’lumli ikkita chiziqli tenglamalar sistemasini hosil qildik. Bu tenglamalar sistemasi berilgan A va B mahsulotlarni ishlab chiqarishda, xom ashyo sarfining matematik modelini ifodalaydi. Biz yuqorida eng od d iy iqtisodiy masalani ko‘rdik, hamda uning modeli ikki noma’lumli ikkita chiziqli tenglamalar sistemasiga keltirilishini ko‘rsatdik. Fan va texnikaning juda ko‘p masalalarining matematik modellari chiziqli tenglamalar sistemasi orqali ifodalanadi. Bu holatlar chiziqli tenglamalar nazariyasini umumiy holda qarashimiz lozimligini ko‘rsatadi.
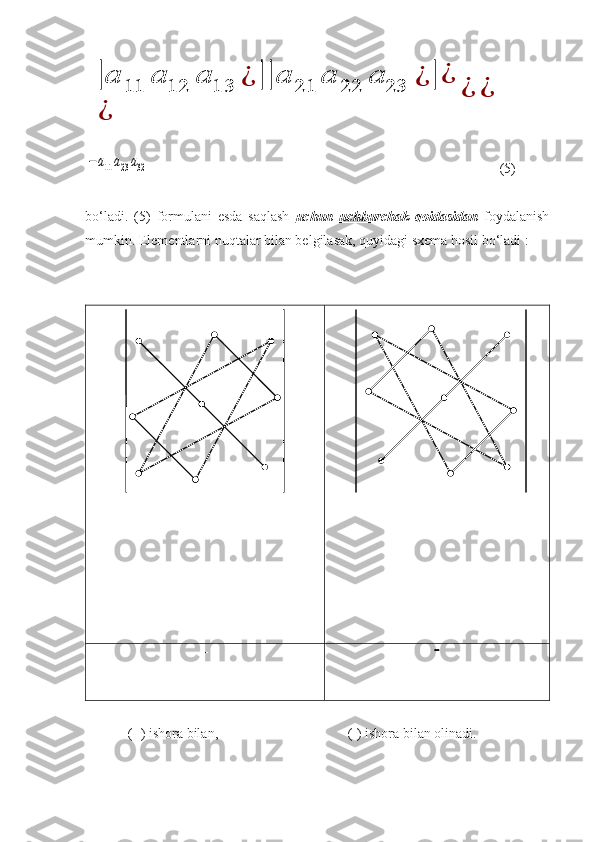
Ikki noma’lumli ikkita chiziqli tenglamalar sistemasi berilgan bo‘lsin: {a11 x1+a12 x2= b1¿¿¿¿ (1) a11 a22 − a12 a21 ≠ 0 bo‘lsa, (1) tenglamalar sistemasi yagona x1= b1a22 − b2a12 a11 a22 − a12 a21 ,x2= b2a11− b1a21 a11 a22 − a12 a21 (2) yechimga ega bo‘ladi. (2) formuladagi sur’at va mahrajdagi ifodalar 2- tartibli determinant (aniklovchi)lar deyiladi. 2-tartibli determinantni a11a22−a12a21=¿ |a11 aalignl ¿12¿¿¿¿|¿ ¿ ¿¿ bilan belgilanadi. a11,a12 ,a21 ,a22 larga determinantning elementlari deyiladi. Shunday qilib, (2) formulalarni determinantlar yordamida x 1 = |b 1 a 12 ¿|¿ ¿ ¿ ¿ ¿ ¿ (3) ko‘rinishda yozish mumkin. Δ = a 11 ¿ |a 22 a 23 ¿ | ¿ ¿ ¿ (4) ifodaga 3- tartibli determinant deyiladi va Δ=¿ |a11a12a13¿||a21a22a23¿|¿ ¿ ¿¿ bilan belgilanadi. a11,a22 ,a33 elementlar bosh diagonalni , a13 ,a22 ,a31 yordamchi diagonalni ifodalaydi. (4) tenglikda 2- tartibli determinantlarni kattaliklari bilan almashtirsak
