Issiqlik o’tkazuvchanlik masalalarini chekli ayirmali sxemalar yordamida yechish.



![t= 0: T = T0,0≤ x≤ L,
x= 0: T= T h,t>0;
x= L:T = Tc,t>0.(4)
chegaraviy masalani qaraymiz.
1.1. To’r va to’r funksiyalar.
Berilgan differentsial tenglamani taqribiy ifodalovchi ayirmali sxemalarni yozish
uchun quyidagi ikkita amal bajarilishi kerak .
1. Argumentning uzluksiz o`zgarish sohasini uning diskret o`zgarish sohasiga
almashtirish kerak ;
2. Differentsial operatorni qandaydir chekli ayirmali operatorga almashtirish,
bundan tashqari chegaraviy shartlar va boshlang`ich ma`lumotlar uchun ayirmali
almashtirishlar tuzish kerak .
Bu jarayon amalga oshirilgandan keyin algebraik tenglamalar sistemasiga o`tamiz.
Uzluksiz argumentning barcha qiymatlari uchun ayirmali masalani y echib bo`lmaydi.
SHuning uchun bu sohada qandaydir chekli sondagi nuqtalar to`plami olinadi va faqat shu
nuqtalarda taqribiy yechim izlanadi. Bunday nuqtalar to`plamiga to`r deyiladi. Nuqtalarning
o`zi esa to`r tugunlari deb ataladi.
To`r tugunlarida aniqlangan funktsiyaga to`rli funktsiya deyiladi.
SHunday qilib differentsial tenglama yechimlari fazosini to`r funktsiyalar fazosi bilan
almashtirdik.
1 - misol . Kesmada tekis to`r.
[0,1 ] kesmani N ta teng bo`lakga bo`lamiz.
h= xi− xi−1=1/N
to`r qadami deb ataladi. Bo`linish nuqtalari xi=ih - to`r tugunlari deyiladi.
Barcha tugunlar to`plami
ωh={xi=ih ,i=1,N−1} to`rni tashkil qiladi. Bu to`plamga
x0=0,xn=1
chegaraviy nuqtalarni qo`shish mumkin, ya`ni ωh={xi=ih,i=0,N} deb
belgilaymiz.
2 - misol. Tekislikda tekis to`r .
D = {0≤ x≤ 1,0≤ t≤ T } sohada aniqlangan ikki
o`zgaruvchili
u(x,t) funktsiyalar to`plamini qaraymiz.
4](/data/documents/e9a99eae-53f5-4d05-8f6d-8378788c522d/page_4.png)
![x o`qining [0,1 ] va t o`qining [0,T] kesmalarini mos ravishda N1
va N2 ta bo`laklarga
bo`lamiz.
h=1/N1,τ=T/N2 bo`lsin. Bo`linish nuqtlaridan o`qlarga parallel to`g`ri chiziqlar
o`tkazamiz. Natijada bu to`g`ri chiziqlar kesishishidan
(xi,tj) tugunlarni hosil qilamiz, ular
ωhτ={(xi,tj)∈D}
to`rni tashkil qiladi.
Bu to`r
x va yo`nalishlar bo`yicha h va τ qadamlarga ega .
S h unga o`xshash kesmada yoki tekislikda notekis to`rni qurish mumkin .
x=(x1,x2)
tekislikda G chegarali murakkab ko`rinishli G soha berilgan bo`lsin.
x1i= ih 1,x2j= jh 2, i,j=0,±1,±2,...,h1,h2>0
to`g`ri chiziqlar o`tkazamiz. U holda
(ih1,jh2)
to`rni hosil qilamiz. « ∘ » bilan ichki, « ¿ » bilan esa tashqi nuqtalar belgilangan.
Ichki nuqtalar to`plamini
ωh bilan, chegaraviy nuqtalar to`plamini γh bilan belgilaymiz.
Shunday qilib
ωh to`r ox1,ox2 yo`nalishlar bo`yicha tekis, ammo G soha uchun ωh= ωh+γh
to`r esa chegara yaqinida notekis.
5](/data/documents/e9a99eae-53f5-4d05-8f6d-8378788c522d/page_5.png)


![2. Issiqlik o’tkazuvchanlik masalalari uchun algoritmlar.
2.1. Oddiy differensial operatorlarning ayirmali approksimatsiyasi.Lv
chiziqli differentsial operator bo`lsin. Lv ga kiruvchi hosilalarni ayirmali
munosabatlar bilan almashtiramiz,
Lv o`rniga shablon deb ataluvchi biror to`r tugunlari
to`plamida
vh to`r funktsiya qiymatlarining chiziqli kombinatsiyasidan iborat Lhvh ni hosil
qilamiz:
Lhvh(x)= ∑
ξ∈Ш (x)
Ah(x,ξ)vh(ξ)
yoki
(Lhvh)i= ∑
xj∈Ш (xi)
Ah(xi,xj)vh(xj)
,
bu erda
Ah(x,ξ) - koeffitsient lar , h - to`r qadami , Ш (x) - x nuqtadagi shablon . Lv ni Lhvh
ga bunday taqribiy almashtirish differentsial operatorni ayirmali operator bilan
approksimatsiyalash deyiladi ( yoki
L operatorning ayirmali approksimatsiyasi deyiladi ).
L
operatorni ayirmali approksimatsiyaga keltirishda shablon tanlash zarur, ya`ni L
operatorni approksimatsiyalash uchun qo`llash mumkin bo`lgan
v(x) to`r funktsiyaning
qiymatlaridan bog`liq bo`lgan
x tugun bilan qo`shni tugunlar to`plamini ko`rsatish kerak.
Lemma . Agar
v∈C(2)[x− h,x+h] bo`lsa
vxx= v(x+h)−2v(x)+v(x− h)
h2 =v''(ξ), ξ= x+θ h,|θ|≤ 1
,
va agar
v∈C(4)[x− h,x+h] bo`lsa
vxx=v''(x)+h2
12 v(4)(ξ), ξ= x+θ1h,|θ1|≤1
,
formulalar o`rinli bo`ladi .
Isbot . Integral shakldagi qoldiq hadi bilan olingan Teylor formulasidan foydalanamiz
v(x)= v(a)+(x− a)v'(a)+...+ (x− a)r
r!
v(r)(a)+ R r+1(x)
, (5)
bunda
8](/data/documents/e9a99eae-53f5-4d05-8f6d-8378788c522d/page_8.png)
![Rr+1(x)= 1
r!∫
a
x
(x− ξ)rvr+1(ξ)dξ = (x− a)r+1
r! ∫
0
1
(1− s)rvr+1(a+s(x− a))ds.
Integral uchun o`rta qiymat haqidagi teoremani qo`llaymiz
Rr+1(x)= (x− a)r+1
(r+1)!
v(r+1)(ξ)
,
bunda
ξ - [a,x] kesmada x ning o`rta qiymati ,
ξ= a+θ (x− a), 0≤ θ≤ 1, ∫
0
1
(1− s)rds = 1
r+ 1
.
( 5 ) da
x n i x+h va a n i x bilan almashtirib , r=1 va r=3 uchun mos ravishda
quyidagilarni olamiz
v(x+h)= v(x)+hv'(x)+h2∫
0
1
(1− s)v''(x+sh )ds
, (6)
v(x+h)= v(x)+hv'(x)+ h2
2
v''(x)+ h3
6
v'''(x)+ h4
6 ∫
0
1
(1− s)3v(4)(x+sh )ds
. (7)
Bu erda
h n i −h ga, s n i −s almashtirib
v(x− h)= v(x)− hv'(x)+h2∫
−1
0
(1+s)v''(x+sh )ds
, (8)
v(x− h)= v(x)− hv'(x)+ h2
2
v''(x)− h3
6
v'''(x)+ h4
6 ∫
−1
0
(1+s)3v(4)(x+sh )ds
(9)
formulalarni olamiz.
(6), (8) dan quyidagini olamiz
vxx= v(x+h)− 2v(x)+v(x− h)
h2 = ∫
−1
1
g2(s)v''(x+sh )ds
,
bunda
g2(s)={
¿1+sagar −1≤s≤0да ,
¿1− sagar 0≤s≤1да .
9](/data/documents/e9a99eae-53f5-4d05-8f6d-8378788c522d/page_9.png)
![g2(s)≥ 0 bo`lganligidan o`rta qiymat haqidagi teoremadan foydalanish mumkin,
natijada
vxx= v''(x+θh )∫
−1
1
g2(s)ds = v''(x+θx )= v''(ξ), − 1≤ θ≤ 1
,
bu y erda
ξ - [x− h,x+h] kesmada o`rta nuqta .
(7) va (9) dan
vxx= v''(x)+ h2
6 ∫
−1
1
g4(s)v(4)(x+sh )ds
hosil qilamiz, bu erda
g
4
( s) = { ¿
( 1 + s ) 3
agar − 1 ≤ s ≤ 0 да ,
¿
( 1 − s ) 3
agar 0 ≤ s ≤ 1 да ,
∫
−1
1
g4(s)ds = 1
2
.
g4(s)≥0
v a v(4)(x) uzluksizligidan , o`rta qiymat haqidagi teoremani qo`llab
vxx= v''(x)+ h(4)
12 (x+θh )
, |θ|≤1
ni olamiz va shu bilan lemma isbotlanadi.
4 misol .
Lv = ∂v
∂x− ∂2v
∂x2 , v= v(x,t) .
(x,t)
- tekislikda nuqta bo`lsin . Shablon ni aniqlaymiz . U to`rtta nuqtadan tashkil
topgan bo`lsin (a rasm ).
10](/data/documents/e9a99eae-53f5-4d05-8f6d-8378788c522d/page_10.png)
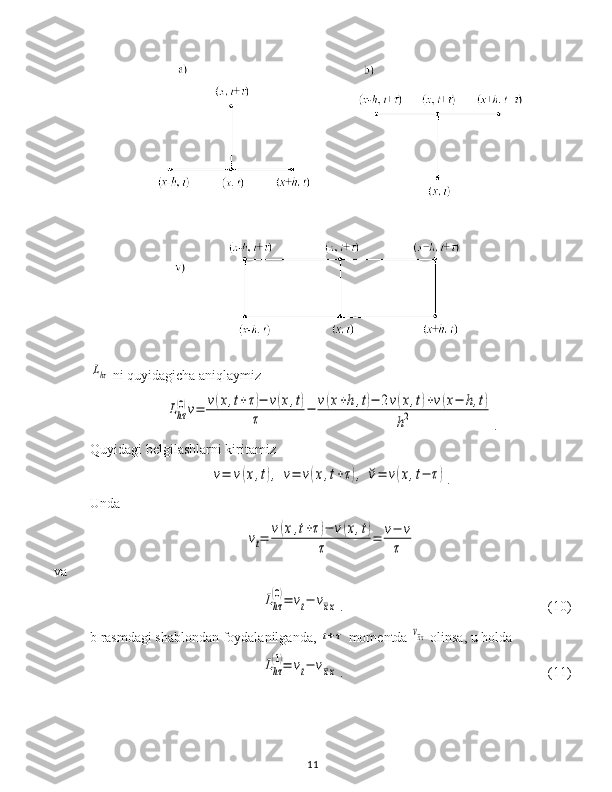

![vtt= (v(x,t+τ)− 2v(x,t)+v(x,t− τ))/τ2.
a) shablonda:
Lhτ v= vtt− vxx
. (14)
To`qqiznuqtali shablonda (g rasm) ayirmali operatorlarning ikkiparametrli oilasini
yozish mumkin
Lhτ
(σ1,σ2)v= vtt− (σ1vxx+(1− σ1− σ2)vxx+σ2˘vxx)
. (15)
(15) dan
σ1= σ2=0 bo`lganda (13), σ2=0,σ1=1 bo`lganda esa (14) kelib chiqadi.
(13), (14), (15) ayirmali operatorlar
O (h2+τ2) approksimatsiya tartibiga ega.
2.2. Ikkinchi tartibli ODT uchun chegaraviy masalalarni o`q otish va chekli
ayirmalar usuli bilan yechish. Progonka usulining turg`unligi.
Chegaraviy masalalarni yechishning sonli usullarini qaraymiz. Ularni ikkita guruhga
ajratish mumkin:
1) Chegaraviy masala y echimini ketma-ket Koshi masalalarini y echishga keltirish;
2) Chekli ayirmalar usullarini qo`llash.
Birinchi guruh usullariga, xususan, o`q otish usuli kiradi.
O`q otish usuli
[0,1] kesmada ikkinchi hosilaga nisbatan yechilgan ikkinchi tartibli tenglama uchun
chegaraviy masalani qaraymiz:
y''= f(x,y,y').
(1 6) H ar qanday kesmani
t=
x− a
b− a
almashtirish yordamida [0,1] kesmaga keltirish mumkin.
Chegaraviy shartni quyidagi oddiy ko`rinishda olamiz
y(0)= y0, y(1)= y1
. (17)
13](/data/documents/e9a99eae-53f5-4d05-8f6d-8378788c522d/page_13.png)











Mavzu: Issiqlik o’tkazuvchanlik masalalarini chekli ayirmali sxemalar yordamida yechish. Reja: I. Kirish. II. Asosiy qism. 1. Chekli ayirmali sxemalar to`g`risida tushunchalar. Differentsial operatorning chekli ayirmali ( CHA ) approksimatsiyasi . Chekli ayirmali masalaning q o` yilishi . 1.1. To’r va to’r funksiyalar. 2. Issiqlik o’tkazuvchanlik masalalari uchun algoritmlar. 2.1. Oddiy differensial operatorlarning ayirmali approksimatsiyasi 2.2. Ikkinchi tartibli ODT uchun chegaraviy masalalarni o`q otish va chekli ayirmalar usuli bilan yechish. 2.3. Chekli ayirmalar usuli. Progonka usulining turg`unligi. 3. Chiziqli bo`lmagan issiqlik o`tkazuvchanlik tenglamasi uchun chekli ayirmali sxemalar tuzish 3.1. Kvazichiziqli issiqlik o`tkazuvchanlik tenglamasi. 3.2. Ayirmali sxema. N’yuton usuli . III. Xulosa. IV. Foydalanilgan adabiyotlar. 1
Kirish Issiqlik o’tkazuvchanlik deb issiqlikni muhitda molekulyar uzatishga aytiladi. Bu jarayon temperaturaning tekis taqsimlanmagan holatida ro’y beradi. Bu holda issiqlik har xil temperaturali zarrachalarning bevosita tutashtirish hisobiga uzatiladi va molekulalar, atomlar va ozod elektronlar orasida energiya almashinuviga olib keladi. Issiqlik o’tkazuvchanlik moddaning agregat holatiga, uning tarkibiga, temperaturasiga, bosimiga va boshqa xarakteristikalariga bog’liq. Ko’p hollarda suyuq holdagi moddaning issiqlik o’tkazuvchanligi gaz holatdagi moddaning issiqlik o’tkazuvchanligidan taxminan o’n marta ko’p bo’ladi. Qattiq jism uchun issiqlik o’tkazuvchanlik erish nuqtasi atrofida suyuqlikka qaraganda (suyuq vismut, olova va tellurdan tashqari) ancha yuqori bo’ladi. Amaliyotda jism ichidagi va uning chegarasi yaqinidagi issiqlik o’tkazuvchanlik har xil bo’lishi tez-tez uchrab turadi. Bu farqlanish issiqlik uzatish jarayoning borish shartlarining o’zgarishi bilan, hamda modda strukturasining o’zgarishi bilan (termik qayta ishlash tekshirish, ko’p ishlatish va hakazo natijasida sodir bo’ladi. Ushbu ishda chiziqli bo’lmagan issiqlik o’tkazuvchanlik tenglamasi uchun chekli ayirmali sxemalar tuzish masalasi qaraladi. Issiqlik o’tkazuvchanlikka tashqi shart- sharoitlar, masalan, nurlanish, bosimning o’zgarishi, magnit maydoni sezilarli ta’sir qilishi mumkin. 2
1. Chekli ayirmali sxemalar to`g`risida tushunchalar. Differentsial operatorning chekli ayirmali ( CHA ) approksimatsiyasi . Chekli ayirmali masalaning q o` yilishi . Nostatsionar issiqlik o’tkazish tenglamasi dekart koordinata sistemasida quyidagi tenglama yordamida yoziladi: ρc ∂ T ∂ t = ∂ ∂ x( λ ∂ T ∂ x ) + ∂ ∂ y ( λ ∂ T ∂ y ) + ∂ ∂ z ( λ ∂ T ∂ z ) + Q w ( x , y , z , t , T ) (1) Bu tenglama (Furye - Kirxgorf) tenglamasi jismning ixtiyoriy nuqtasidagi temperaturaning fazoviy va vaqtga bog’liq o’zgarishlarini bog’lab turadi. Bu yerda ρ−¿ zichlik, c − ¿ nisbiy issiqlik sig’imi, λ−¿ issiqlik o’tkazuvchanlik koeffisiyenti, Qw(x,y,z,t,T) -issiqlik manbayining ichki quvvati. tenglama konduktiv issiqlik uzatish jarayoni rivojlanishining ko’plab variantlarini ifodalaydi. Son-sonoqsiz variantlardan bittasini tanlash va unga to’liq matematik bayon qilish uchun (1) tenglamaga bir qiymatlilik shartini qo’yish kerak. Bu shart geometrik , fizik, boshlang’ich va chegaraviy shartlarni o’z ichiga oladi. Issiqlik o’tkazuvchanlik koeffisiyenti ko’p xollarda temperaturaga bog’liq bo’ladi. Masalan UO 2 urandioksidining Issiqlik o’tkazuvchanlik koeffisiyentini xisoblash uchun quyidagi bog’liqlikdan foydalaniladi: λ(T )= 5500 560 +T +0.942 ⋅10 −10 T 3 (2) Bu xolda bir o’lchovli chiziqli bo’lmagan issiqlik o’tkazuvchanlik tenglamasi quyidagi ko’rinishda bo’ladi: ρс ∂ T ∂t = ∂ ∂ x (λ(T )∂ T ∂ x ),0< x< L . (3) (3) tenglama uchun 3
t= 0: T = T0,0≤ x≤ L, x= 0: T= T h,t>0; x= L:T = Tc,t>0.(4) chegaraviy masalani qaraymiz. 1.1. To’r va to’r funksiyalar. Berilgan differentsial tenglamani taqribiy ifodalovchi ayirmali sxemalarni yozish uchun quyidagi ikkita amal bajarilishi kerak . 1. Argumentning uzluksiz o`zgarish sohasini uning diskret o`zgarish sohasiga almashtirish kerak ; 2. Differentsial operatorni qandaydir chekli ayirmali operatorga almashtirish, bundan tashqari chegaraviy shartlar va boshlang`ich ma`lumotlar uchun ayirmali almashtirishlar tuzish kerak . Bu jarayon amalga oshirilgandan keyin algebraik tenglamalar sistemasiga o`tamiz. Uzluksiz argumentning barcha qiymatlari uchun ayirmali masalani y echib bo`lmaydi. SHuning uchun bu sohada qandaydir chekli sondagi nuqtalar to`plami olinadi va faqat shu nuqtalarda taqribiy yechim izlanadi. Bunday nuqtalar to`plamiga to`r deyiladi. Nuqtalarning o`zi esa to`r tugunlari deb ataladi. To`r tugunlarida aniqlangan funktsiyaga to`rli funktsiya deyiladi. SHunday qilib differentsial tenglama yechimlari fazosini to`r funktsiyalar fazosi bilan almashtirdik. 1 - misol . Kesmada tekis to`r. [0,1 ] kesmani N ta teng bo`lakga bo`lamiz. h= xi− xi−1=1/N to`r qadami deb ataladi. Bo`linish nuqtalari xi=ih - to`r tugunlari deyiladi. Barcha tugunlar to`plami ωh={xi=ih ,i=1,N−1} to`rni tashkil qiladi. Bu to`plamga x0=0,xn=1 chegaraviy nuqtalarni qo`shish mumkin, ya`ni ωh={xi=ih,i=0,N} deb belgilaymiz. 2 - misol. Tekislikda tekis to`r . D = {0≤ x≤ 1,0≤ t≤ T } sohada aniqlangan ikki o`zgaruvchili u(x,t) funktsiyalar to`plamini qaraymiz. 4
x o`qining [0,1 ] va t o`qining [0,T] kesmalarini mos ravishda N1 va N2 ta bo`laklarga bo`lamiz. h=1/N1,τ=T/N2 bo`lsin. Bo`linish nuqtlaridan o`qlarga parallel to`g`ri chiziqlar o`tkazamiz. Natijada bu to`g`ri chiziqlar kesishishidan (xi,tj) tugunlarni hosil qilamiz, ular ωhτ={(xi,tj)∈D} to`rni tashkil qiladi. Bu to`r x va yo`nalishlar bo`yicha h va τ qadamlarga ega . S h unga o`xshash kesmada yoki tekislikda notekis to`rni qurish mumkin . x=(x1,x2) tekislikda G chegarali murakkab ko`rinishli G soha berilgan bo`lsin. x1i= ih 1,x2j= jh 2, i,j=0,±1,±2,...,h1,h2>0 to`g`ri chiziqlar o`tkazamiz. U holda (ih1,jh2) to`rni hosil qilamiz. « ∘ » bilan ichki, « ¿ » bilan esa tashqi nuqtalar belgilangan. Ichki nuqtalar to`plamini ωh bilan, chegaraviy nuqtalar to`plamini γh bilan belgilaymiz. Shunday qilib ωh to`r ox1,ox2 yo`nalishlar bo`yicha tekis, ammo G soha uchun ωh= ωh+γh to`r esa chegara yaqinida notekis. 5
