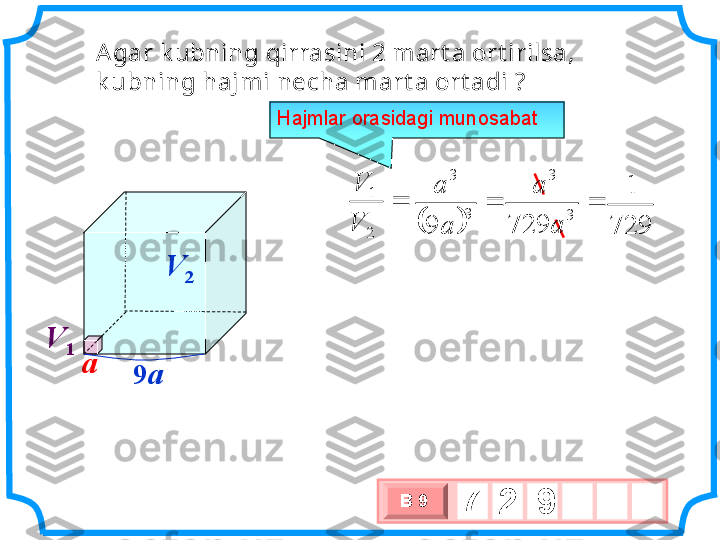
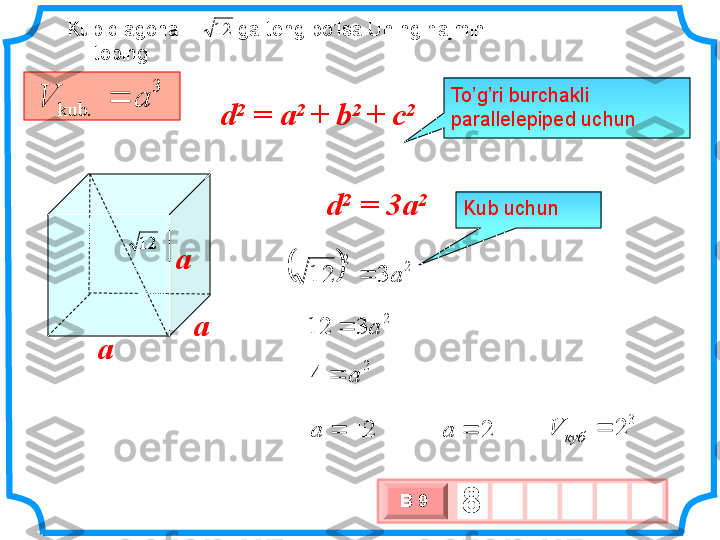
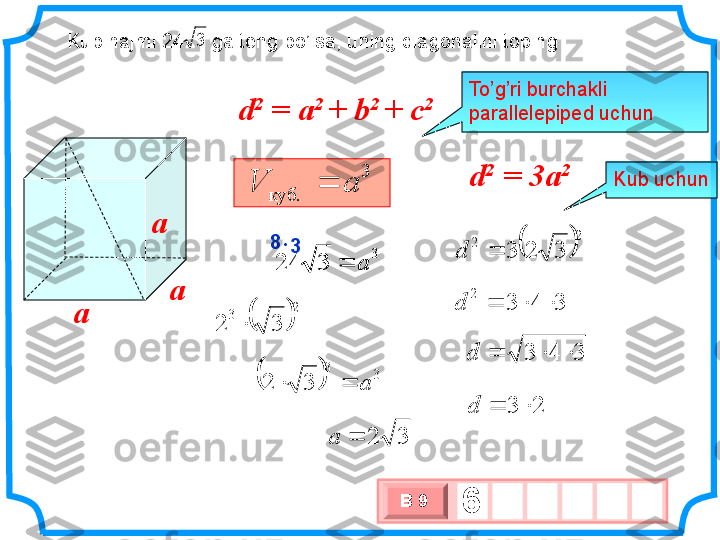
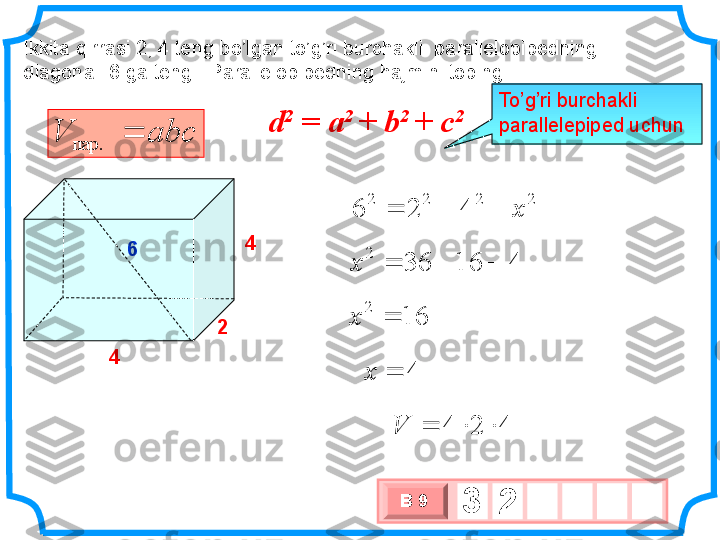
silindr prizma Hajm

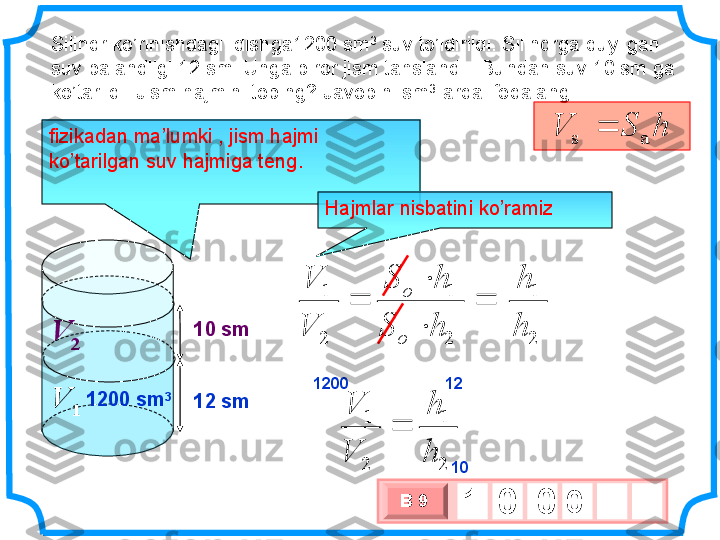

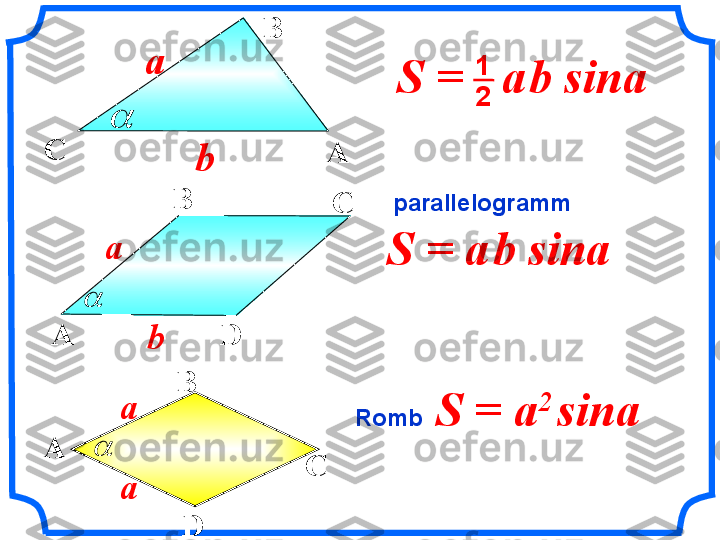
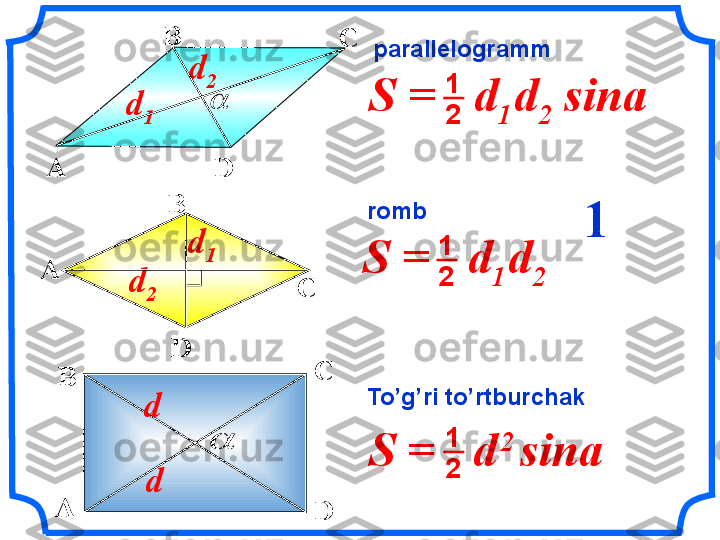
10 sm V 2Silindr ko’rinishdagi idishga 1200 sm 3 suv to’ldirildi . Silindrga quyilgan suv balandligi 12 sm . Unga biror jism tahslandi . Bundan suv 10 sm ga ko’tarildi . Jism hajmini toping ? Javobini sm 3 larda ifodalangh S V a s 2 1 V V 2 1 h S h S o o 2 1 h h 2 1 V V 2 1 h h1200 12 1012 sm1200 sm 3 V 1fizikadan ma’lumki , jism hajmi ko’tarilgan suv hajmiga teng . Hajmlar nisbatini ko’ramiz 3 х 1 0 хВ 9 0 1 0 0
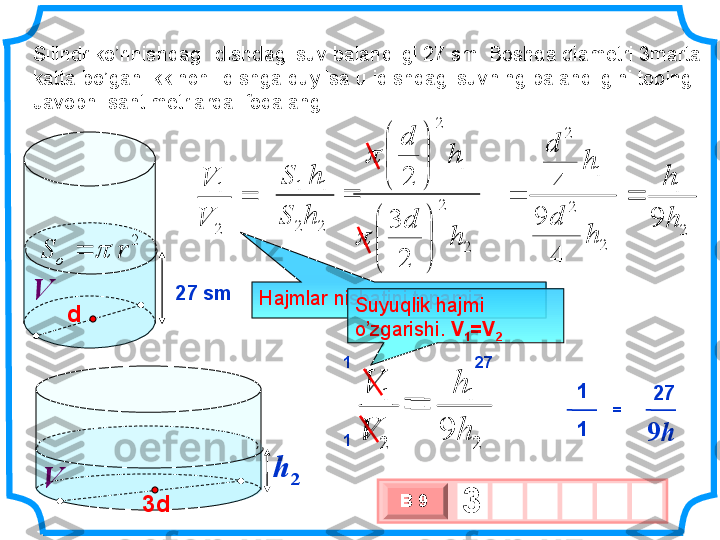
Silindr ko’rinishdagi idishdagi suv balandligi 27 sm . Boshqa diametri 3marta katta bo’gan ikkinchi idishga quyilsa u idishdagi suvning balandligini toping Javobni santimetrlarda ifodalang 2 1 V V 2 2 1 1 h S h S 2 2 1 2 2 3 2 h d h d 2 1 V V 2727 smV 3 х 1 0 хВ 9 3h 2 V d 3d2 rS o 22 12 4 9 4 h d h d 21 9 hh 21 9 h h1 1Hajmlar nisbatini topamiz V VSuyuqlik hajmi o’zgarishi . V 1 =V 2 271 1 9 h=
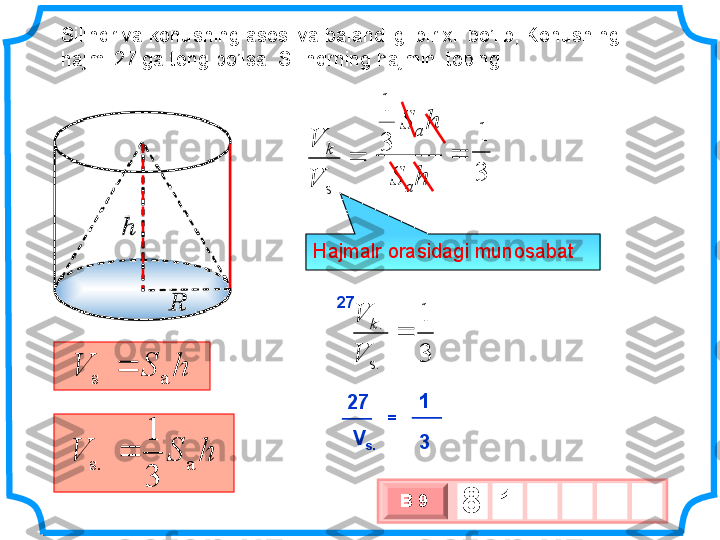
To’g’ri burchakli muntazzam prizmaning katetlari 6 va 8 bo’lsa, Yon qirralai teng . Tashqi chizilgan silindr hajmini toping 3 х 1 0 хВ 9 1 2 5 5 568 105 h S V a s. h r V 2 s. 5 5 2 s V 5 25
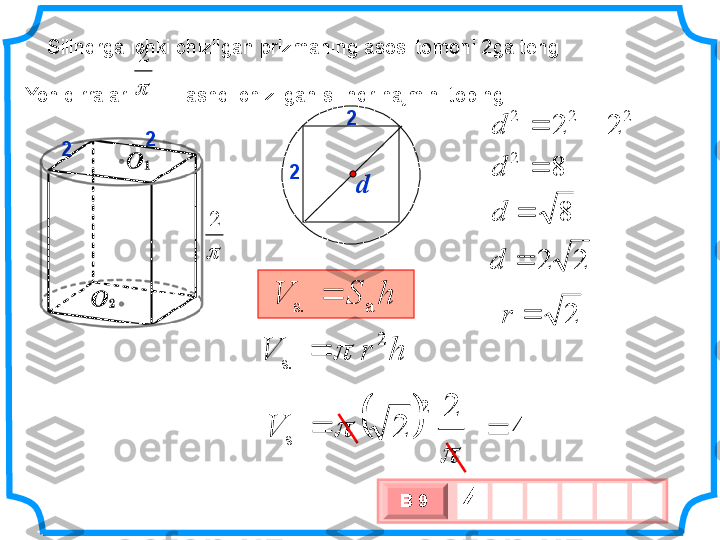
2 2 2 s V Silindrga ichki chizilgan prizmaning asosi tomoni 2ga teng Yon qirralari . Tashqi chizilgan silindr hajmini toping 3 х 1 0 хВ 9 4 2 2 h S V a s. h r V 2 s. 4 2 2 2 2 2 2 2 2 2 d 8 2 d 8 d 2 2 d 2 r d
