Trigonometriya










Trigonometriya
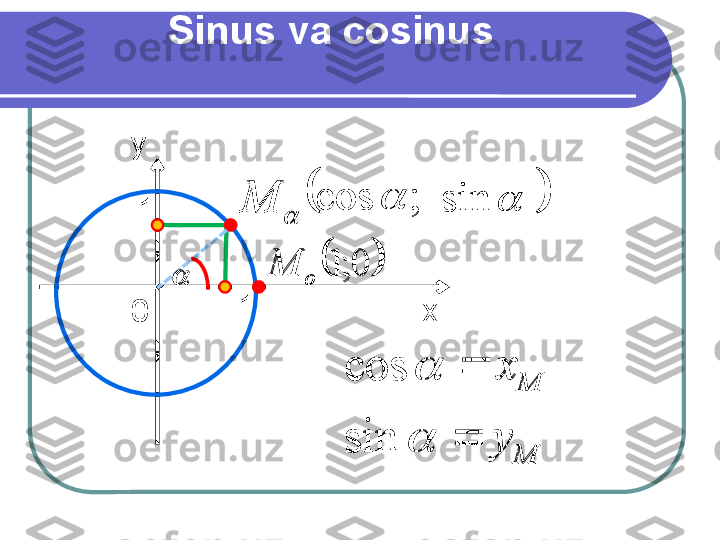
Sinus va cosinus xy 0 11 M sin ; cos 0; 1 o M M M y x sin cos M sin ; cos 0; 1 o M M M y x sin cos
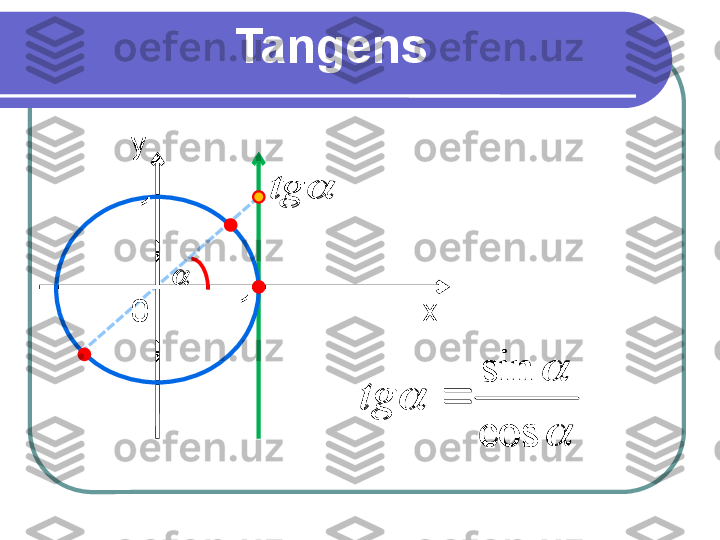
Tangens xy 0 11 tg cos sin tg tg cos sin tg
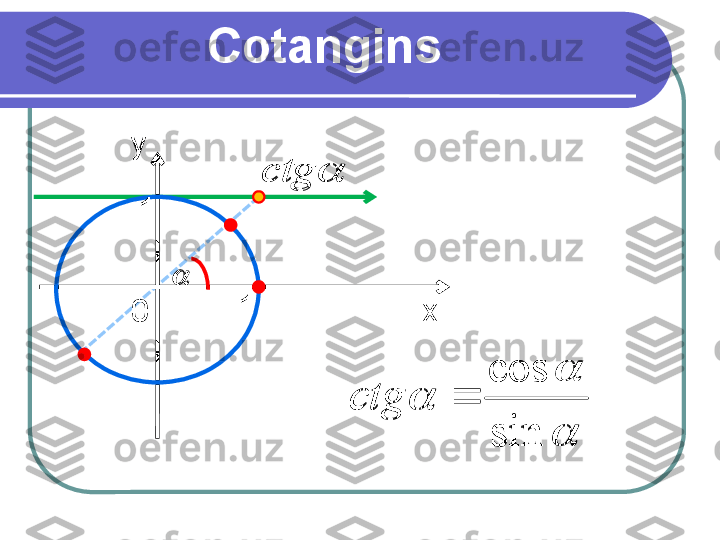
Cotangins xy 0 11 ctg sin cos ctg ctg sin cos ctg
Asosiy f ormulalar x ctg ctg tg x tg 2 2 2 2 1 4 3 1 2 cos sin 1 1 x 2 cos 1 1 x 2 sin 1 x ctg ctg tg x tg 2 2 2 2 1 4 3 1 2 cos sin 1 1 x 2 cos 1 1 x 2 sin 1
