logo
  1. Bosh sahifa
  2. Diplom ishlar
  3. Umumiy
  4. TEKIS ALGEBRAIK EGRI CHIZIQLARNI ULARNING KO’PYOQLIKLARI YORDAMIDA TADQIQ QILISH

TEKIS ALGEBRAIK EGRI CHIZIQLARNI ULARNING KO’PYOQLIKLARI YORDAMIDA TADQIQ QILISH

Yuklangan vaqt:

20.11.2024

Ko'chirishlar soni:

0

Hajmi:

1010.7763671875 KB
Ko'chirib olish
TEKIS ALGEBRAIK EGRI CHIZIQLARNI ULARNING KO’PYOQLIKLARI YORDAMIDA TADQIQ QILISH Mundarija KIRISH 3 I bob. Geometriyalar 1.1. Evklid va Affin geometriyasi 4 1.2. Proyektiv va Algebraik geometriya 6 1.3. Darajali geometriya 10 II bob. Darajali geometriya asoslari 2.1. Analitik funksiyalarning lokal masalalari 12 2.2. Funksiyalarning kichiklik tartibi 15 2.3. Tekis egri chiziqlarning kichiklik tartibi 16 2.4. Analitik funksiyalarning lokal xossalari 19 III bob . Tekis algebraik chiziqlarni ularning ko ’ pyoqliklari yordamida tadqiq qilish 3.1. Oddiy nuqtaning lokal tahlili. 34 3.2. Haqiqiy egri chiziqning eskizi. 41 3.3. Ishlab chiqilgan algoritmlarning misollar yechishga tadbiqlari 43 3.4. Darajali geometriya dasturiy ta'minoti haqida 49 XULOSA 52 FOYDALANILGAN ADABOYITLAR RO’YXATI 53 1 KIRISH Bitiruv malakaviy ishining dolzarbligi: Ushbu bitiruv malakaviy ishida keyingi yillarda keng o‘rganilayotgan sohalardan biri bo‘lgan darajali geometriya asoslari va uning tekis algebrik chiziqlarning xossalarini o’rganishga tadbiqlari o‘rganilgan. Jumladan, darajali geometriyaning asosiy tushunchalari, uning muhim elementlari hamda tadbiqlari o‘rganilgan. Bitiruv malakaviy ishining maqsadi: darajali geometriya metodlarini tekis algebrik chiziqlarning xossalarini o‘rganish uchun tadbiqlaridan iboratdir. Bitiruv malakaviy ishining vazifalari: Bitiruv malakaviy ishining vazifalari darajali geometriya metodlarini tekis algebrik chiziqlarning xossalarini o‘rganish uchun tadbiq etish, bu yo‘nalishga qizziqgan va o‘rganishni istagan talabalar, magistrlar va yosh olimlar uchun o‘zbek tilida muhim ma’lumotlar bazasini shakllantirishdan iborat. Bitiruv malakaviy ishining o ‘ rganilganlik darajasi: Ushbu malakaviy bitiruv ishida qo’yilgan talablar bajarildi, qo’yilgan vazifa yuzasidan ma’lumotlar o‘rganildi. Darajali geometriya, Nyuton ko’pyoqligi, qisqartma tenglamalar, algebraik chiziqlar va ularning eskizlarini yaratishda A.D. Bryuno, A.S.Soleev, A.B. Batxin, H.Nosirova, X. Ro’zimuradovlarning monongrafyalari [8], ilmiy maqolalaridan [1, 10, 20] foydalanildi. Bitiruv malakaviy ishining ob’yekti: Ushbu ishning ob’yekti tekis algebraik chiziqlar, ularning tashuvchilari, Nyuton ko’pyoqliklari, kompyuter algebrasi tizimlari hisoblanadi. Bitiruv malakaviy ishining predmeti: har xil geometriylar, darajali geometriya asoslari va usullaridan iborat. Bitiruv malakaviy ishida qo ‘ llanilgan metodikaning tavsifi: Ishda chiziqli va abstrakt algebraning usullaridan, geometrik usullar, matematik analiz usullari hamda daragali geometriya usullaridan foydalanilgan. 2 Bitiruv malakaviy ishi mundarija, kirish, uchta bob, xulosa va foydalanilgan adabiyotlar ro ‘ yxatidan iborat. Adabiyotlar ro ‘ yxati o’z ichiga keyingi yillarda nashr qilingan 23 ta adabiyotni olib, 54 betdan tashkil topgan. I bob. Geometriyalar 1.1. Evklid va Affin geometriyasi Geometriya turli jismlarning tuzilishini, figuralarni va ularning nisbiy holatini o'rganadi. Intuitiv ravishda hamma bu nima ekanligini tushunadi. Lekin birinchi marta geometriyaning ta'rifini F. Klein 1872 yilda Erlangen dasturida quyidagicha bergan: "Geometriya ikkita ob'ektning: fazo va uning almashtirishlari gruppasining kombinatsiyasidan iborat.” Agar har bir A koordinatalar almashtirishi bilan birga uning teskari almashtirishi A−1 mavjud bo’lsa, A∙A−1 almashtirishlar ko’paytmasi hech narsani o'zgartirmaydigan ayniy almashtirish bo'ladi. Turli fazolar va turli gruppalarning o’zaro ta’siri natijasida turli geometriyalar hosil bo’ladi. Quyida biz har biri avvalgisini o'z ichiga oladigan geometriyalarning ma'lum bir ketma-ketligini qarab chiqamiz. Bular Evklid, affin, proyektiv, algebraik va darajali geometriyalardan iborat. Barcha geometriylar bitta fazoda - haqiqiy n o'lchovli fazo R n quriladi, lekin har safar almashtirishlar gruppasi kengayadi. Evklid geometriyasi Bu yerda R n fazoda biz qo‘yidagi vektor uzunligini qaraymiz: ¿∨ X∨¿≝⟨X ,X ⟩ va X ∗ = AY ∗ almashtirishlar gruppasi ta’sirida bu uzunlik saqlanadi: ⟨ X,X ⟩ = ⟨ AY ∗ , AY ∗ ⟩ = ⟨ Y ,A ∗ AY ∗ ⟩ = ⟨ Y,Y ⟩ ya'ni A ∗ A = E — birlik matritsasi, E=( 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ 1) , 3 yokiA¿= A−1 . Bunday xususiyatga ega matritsalar ortogonal deyiladi. Ular R maydon ustida ortogonal xosmas kvadrat matritsalarning O ( n ) gruppasini hosil qiladi. Almashtirishlar gruppasi parallel ko’chirishni ham o'z ichiga oladi: X = X 0 + Y , (2.1) bu erda X 0 - tayinlangan vektor. Ushbu almashtirishlar ta’sirida burchaklar, yuzalar va hajmlar saqlanadi. Affin geometriyasi Bu erda ikkita fazo mavjud: asosiysi haqiqiy R n = { X = ( x 1 , x 2 , … , x n ) | x i ∈ R n , i = 1,2 , … , n } va unga qo’shma (ya'ni dual) bo’lgan R ¿ n = { Y = ( y 1 , y 2 , … , y n ) | y i ∈ R n , i = 1,2 , … , n } fazolar qaraladi. Bu yerda X ¿ = A X ' ∗ ¿ , Y ¿ = B Y ' ∗ ¿ ; det A , det B ≠ 0 ¿ ¿ almashtirishlar o’zaro qo’shma fazolarni vektorlarining skalyar ko’paytmalarini saqlaydi: ⟨ X , Y ⟩ = ¿ bu yerda X , X ' ∈ R n , Y , Y ' ∈ R ¿n dan iborat. Demak, A ∗ B = E, ya'ni B = ( A ∗ ) −1 . R n fazoning o’ziga o’zaro bir qiymatli affin akslantirishlari to'plami akslantirishlarini ko’pyatirish (ketma-ket bajarish)ga nisbatan gruppa tashkil qiladi va u Aff R n bilan belgilanganadi. Bu gruppa n-tartibli xosmas matrisalardan tashkil topgan to'la chiziqli gruppa GL(n,R) ga akslanadi, affin almashtirishlar gruppasiga (2.1) ko’rinishdagi parallel ko’chirishlar ham kiradi. Ushbu geometriyada to'g'ri chiziqlar, tekisliklar va har qanday chiziqli ko’pxilliklar mos ravishda to'g'ri chiziqlar, tekislik va chiziqli ko’pxilliklarga o’tadi. Bunday holda, 4 burchaklar saqlanib qolmaydi, lekin to'g'ri va dual fazolar vektorlari orasidagi ortogonallik saqlanib qoladi:⟨ X,Y ⟩ = 0=¿ ⟨X',Y'⟩ Ikki vektorning skalyar (yoki ichki) ko'paytmasidan tashqari n − 1 ta X1,... ,Xn−1∈Rn vektorlarining tashqi ko’paytmasi ham mavjud va u quyidagicha aniqlanadi. det ( I X 1 ⋮ X n − 1 ) = y1i1+… +ynin , bu yerda I=(i1,… ,in) va Y = ( y 1 , … , y n ) ∈ R n , X1,... ,Xn−1 . vektorlariga normal Y vektorni hisoblash imkonini beradi 1.2. Proyektiv va Algebraik geometriya Proyektiv geometriya. Quyidagi muammoni qarab chiqamiz: 2.1.-misol. Tekislikda L 1 va L2 parallel to’g’ri chiziqlar, ularga ortogonal M to’g’ri chiziq va kuzatish nuqtasi N berilgan bo’lsin. N nuqtadan M to’g’ri chiziqqa L1 va L2 to’g’ri chiziqlar qismlarini x → ∞ bo’lganda proyeksiya qilish talab qilinadi (2.1-rasm). 2.1-rasm. 5 Li chiziqlarning M chiziqqa barcha proyeksiyalari bir N'∈ M nuqtada tugaganligi uchun, bu nuqtada kuzatish nuqtasidan o’tuvchi L 0 chiziq M bilan kesishadi va L1 va L2 chiziqlarga parallel bo'ladi. Bu muammo rasmda uzoqlashib borayotgan to'g'ri chiziqlarni tasvirlashda paydo bo'ladi. Bu yerda L 1 va L2 chiziqlar mos ravishda pol va ship, N nuqta - rassomning ko'zi (yoki kamera), M – rasm yoki manzara yotgan tekislikning to‘rtburchakli qismi (polotno)dan iboart . Bu xususiyat kengaytiril ayot gan fazoviy ob'ektlarni bir tekis likda tasvirlashda paydo bo'ladi. Bunday holda, rasmda cheksizlikka mos keladigan bitta nuqta (markaz) paydo bo'ladi. Ammo taniqli rassomlarning ko'plab rasmlari ko'proq ifodalash uchun bir nechta markazlarga ega. To'g'ri chiziqli proyeksiyalash natijasida saqlanib qolanadigangan xususiyatlar bilan proyektiv geometriya bilan tavsiflanadi. Proyektiv geometriyada almashtirishlar gruppasi proyektiv gurappa deb ataladigan P ( R n ) gurppadan iborat bo‘ladi . Bu yerda bir jinsli koordinatalar sistemasi u0,u1,... ,un kiritadi : xi= ui u0 , i=1,… ..,n va qo‘yidagi chiziqli almashtirishlar amalga oshiriladi U =(u0,... ,un)= VB , Bu yerda V=(v0,... ,vn) , B − n + 1 o'lchamdagi kvadrat matritsadan iborat, det B≠0 . Bu yerda xi= ui u0 = ⟨V ,Bi⟩ ⟨V ,B0⟩ bo‘ladi, bu yerda B=(B0¿,B1¿,… Bn¿) va Bi¿ - B matritsasining ustunlari. Ya'ni , bu yerda almashtirishlarda chiziqli maxrajlar mavjud. Bundan tashqari, R n fazo cheksiz uzoql ashgan u 0 = 0 gipertekislik bilan to'ldirilgan. Bu yerda. y i = v i v 0 = f i ( X ) f 0 ( X ) , i=1,… ,n. Algebraik geometriya. Bu geometriya fi(X)=0,i=1,... ,m , algebraik (ya’ni polinom) tenglamalar tizimi orqali R n da aniqlangan algebraik ko’pxilliklarni o’rganadi, bu yerda f i — ko’phad (polinoml). Bunday holda, qo’yidagi biratsional almashtirishlar qaraladi. xi= pi(Y) qi(Y) yi= ri(X) si(X) , i = 1 , … , n 6 bu yerda pi,qi,ri,si — polinomlardan iborat. Bunday almashtirishlar bilan egri chiziqlar to'g'ri chiziqlarga aylanishi mumkin va aksincha. 2.2- misol. Qo’yidagi tenglama bilan berilgan Dekart yaprog’i deb ataladigan egri chizig'ini qarab chiqamiz: x 13 + x 22 − 3 x 1 x 2 =0 (2.2) va uni bitta o'zgaruvchi bilan parametrlashga harakat qilamiz. x1,x2 tekislikda bu egri chiziq 2.2 rasmda tasvirlangan. x 1 = x 2 = 0 nuqta uning qo'sh nuqtasidir. 2.2-rasm x2=kx1 almashtiriashni (2.2) tengalmaga qo’yamiz. Hosil bo’lgan tenglamani x 12 ga qisqartirib olamiz: x 1 + k 3 x 1 − 3 k = 0. Bu yerdan x1 va x2 larni k bilan ifodalab olamiz, ya’ni, x 1 = 3 k 1 + k 3 , x 2 = 3 k 2 1 + k 3 , k= x2 x1 (2.2’) (2.2) egri chiziqning har bir ( x 1 , x 2 ) ≠ 0 nuqtasiga burchak koeffisiyenti k bo’lgan yagona to'g'ri chiziq x2=kx1 mos keladi, bu yerda k izlangan parametr dan iborat. (2.2’) tenglamalar Dekart yaprog’ining parametrik tenglamasidan iborat. 7 2.3-misol. x 12 + x 22 = 1 aylananing parametrik tenglamasini topamiz. Aylananing x 1 = 0 , x 2 = 1 nuqtadan boshlab har bir nuqtasiga bitta to‘g‘ri chiziq x 2 − 1 = k x 1 va x 1 o’qning bitta nuqtasi mos keladigan parametrlashni topamiz. Bu chiziqlar kesishadi. Aylanada yotgan x 1 = 0 , x 2 = 1 nuqta orqali burchak koeffisiyenti k bo'lgan to'g'ri chiziq o’tkazamiz. Uning tenglamasi x 2 − 1 = kx 1 , (2.3) boladi, bu erdan x2=1+kx1 . Bu qiymatni aylana tenglamasiga qo'yib, quyidagi tenglamani olamiz: x 12 + ( 1 + k x 1 ) 2 − 1 = x 1 [ x 1 ( 1 + k 2 ) + 2 k ] = 0 Bu tenglama (2.3) bilan birgalikda ikkita yechimga ega x1= 0,x2=1 x 1 = − 2 k 1 + k 2 , x2= 1−k2 1+k2 , (2.4) (2.4) almashtirish k→ (x1,x2) almashtirishni, (2.3) formula esa teskari almashtirish (x1,x2)→ k ni beradi: k = y − 1 x Biz biratsional almashtirishlarga erishamiz. Bu yerda parametr burchak koeffisiyent k yoki B=(−1/k,0) nuqtadan iborat. 8 Algebraik geometriyada quyidagi teorema mavjud. 2.1. teorema. Ord f≤n bo’lgan f(X)= 0 tenglama bilan aniqlangan algebraik ko’pxillik har doim R n − 1 fazosiga biratsional ekvivalentdir. Ushbu geometriyada nuqtani to'g'ri chiziq yoki tekislikkacha davom ettirish mumkin va R n fazo esa cheksiz uzoqlashgan R ∞ n − 1 gipertekislik bilan to'ldiriladi. 1.3. Darajali geometriya X = ( x 1 ,...,x n ) , Q = ( q 1 ,...,q n ) , XQ= x1q1∙∙∙xnqn=¿ exp ⟨ ln X,Q ⟩ bo’lsin, bu yerda ln X = ( ln x 1 ,..., ln x n ) . ln X = ln Y · A (2.5) almashtirish X Q ni Y QA ga o’tkazadi, chunki ⟨ ln X,Q ⟩ , = ⟨ ln Y,Q A¿⟩ , Qo’yidagi yig’indini qarab chiqaylik, ∑i biXQi (2.5) almashtirish natijasida bu yig'indidan ∑i biYQiA¿ (2.6) yig’indini hosil qilamiz. Agar barcha Q i bitta L gipertekisligida yotsa, ya'ni ⟨ Q i , N ⟩ = c = const, u holda Q → QA ∗ chiziqli almashtirish gipertekislik L ni p n = c = const gipertekislikka o’tkazadi. U holda (2.6) yig'indi y n ning faqat c darajalarini o'z ichiga oladi, y nc ko’paytuvchini qavsdan chiqarilgandan keyin va y nc qisqartirilgandan so’ng faqat y 1 ,...,y n −1 o'zgaruvchilardan bo’g’liq bo’lgan ko’phad qoladi. Bu yerda Q ∈ R n vektor ko’rsatkichlari uchun affin geometriysi hosil bo’ladi. Bunda ln X , ln Y vektorlari qo’shma R¿n fazoda yotadi. Darajali geometriya (2.1) parallel ko’chirishni, X = Y A chiziqli almashtirishlar va (2.5) darajali almashtirishni o’z ichiga oladi. Ikkinchi bobda darajali geometriyaning tekislikdagi xossalari o’rganiladi. 9 II BOB Darajali geometriya asoslari 2.1 – §. Analitik funksiyalarning lokal masalalari . I. Oddiy nuqta . Quyidagi f(x1,x2)=0 (3) tenglamani qaraymiz. Bunda f(x1,x2) funksiya uchun f ( 0,0 ) = 0 bo’lib, f x1= x2=0 nuqtada analitik funksiya bo’lsin, ya’ni f ni (4) darajali qatorga yoyish mumkin bo’lib, bunda fq1q2 – koeffitsientlar o’zgarmas sonlar, (4) qator nolning qandaydir | x 1 | < ε , |x2|<ε atrofida yaqinlashuvchi va f10=0 bo’lsin. (4) qatorni yoyib yozsak: f = f 10 x 1 + f 01 x 2 + f 20 x 12 + f 11 x 1 x 2 + f 02 x 22 + ¿ … ¿ 2.1 – Teorema . f funksiya nolda analitik, f ( 0,0 ) = 0 , f01≠0 bo’lsin. U holda (4) tenglamaning darajali qatorga yoyish mumkin bo’lgan yechimga ega, ya’ni: x2= a(x1)= ∑ k=1 ∞ akx1k (5) Isbotda noma’lum koeffitsiyentlar usulidan foydalanamiz. (5) ni (4) ifodaga qo’yamiz va ∑ q1,q2>0 fq1q2x1 q1 (∑ k=1 ∞ akx1 k ) q2=0 (6) ni hosil qilamiz. (6) ning chap qismidagi x 1 o’zgaruvchining darajasi l ga teng bo’lgan barcha hadlarini yozib chiqamiz. 10 ∑ fq1q2ak1...x1q1x1k1...x1ks Bu had x 1 bo’yicha l = q 1 + k 1 + ... + k s … darajaga ega bo’ladi. Bunda a k koeffitsient ak−1 dan keyin keladi (koeffitsientlar tartiblangan). Bu hadlar ichidan k indeksi katta bo’lgan a k ni olamiz. Bu holda q 1 = 0 bo’lishi aniq. Bunda k ning eng katta qiymati k=l da bo’ladi. Bunday had f01al bo’ladi. Boshqa barcha hadlarni ∑ l' ❑ bilan belgilaymiz. Ularda a k faqat k < l bo’lgan indekslar bilan kiradi. Agar f(x1,a(x1))≡0 bo’lsa, (6) tenglik o’rinli bo’ladi. Bundan f 01 a l + ∑ l' ( a 1 … a k − 1 ) ko’rinishdagi koeffitsientlar uchun tenglamalar sistemasini hosil qilamiz va l bo’yicha ketma – ket al=−∑l ' ¿f01 ni aniqlab olamiz. Mojaranta usulidan foydalanib (5) qatorning x1 ning yetarlicha kichik | x 1 | < ε 1 atrofda yaqinlashishini ko’rsatish mumkin. Bu Koshining oshkormas funksiya haqidagi teoremasidir. x1,x2 o’zgaruvchilar tekisligida (3) tenglamaning x 2 = a ( x 1 ) yechimlari noldan o’tuvchi oddiy egri chiziqdan iborat bo’ladi. (5) yoyilmani har xil yo’llar bilan hisoblash mumkin. Masalan ∑ l' ❑ ko’phadni a j va f q 1 q 2 koeffitsientlarning funksiyasi sifatida yozish mumkin. Boshqa usuli: (5) qator ketma – ket yaqinlashtirish yordamida izlanishi mumkin. Buning uchun berilgan (3) tenglamada x2=a1x1+y1 almashtirish olinadi. Bu holda (3) tenglama f 1 ( x 1 , y 1 ) = 0 tenglamaga o’tadi va bundan 11 y 1 = ∑ k = 0∞ a k x 1k (7) yechimni topish kerak bo’ladi. Keyingi yaqinlashishlarda yk=ak+1x1k+1+yk+1 olish kerak. 1 – misol . f= x1+x2+x1x2 . (4) dagi belgilashga ko’ra f10=1 , f01=1 , f11=1 , f00=0 va h.k. f da x2= a1x1+y1 almashtirish olamiz. Natijada x1+a1x1+y1+x1(a1x1+y1)=0 ni hosil qilamiz. (7) dan ko’rinib turibdiki, y1 - o’zgaruvchili x1 bo’yicha chiziqliga ko’ra yuqoriroq tartibga ega bo’lyapti. Birinchi tartibli hadlarni ajratib, ular uchun x1+a1x1=0 tenglamani hosil qilamiz. Bundan a1=−1 ni topamiz. y1 uchun y1− x12+y1x1=0 tenglamani hosil qilamiz. Ikkinchi y1= a2x12+y2 yaqinlashishda f= a2x12+y2− x12+a2x13+x1y2= 0 ga ega bo’lamiz. x1 bo’yicha ikkinchi tartibli hadlar uchun a2x12− x12= 0 ni hosil qilamiz. Bundan a2=1 . Demak, f= y2+x13+x1y2= 0 Xuddi shunday uchinchi yaqinlashish y2=a3x13+y3 uchun f= a3x13+ y3+x13+a3x14+x1y3= 0 12 ni hosil qilamiz. Eng kichik tartibli (bu yerda uchinchi) hadlar uchun a3x13+x13= 0 bo’lib, a3=−1 . Xuddi shunday davom ettirsak, x=∑ k=1 ∞ (−x1)k hosil qilamiz. Ikkinchi tomondan x1+x2+x1x2= 0 tenglamani x2 ga nisbatan yechish mumkin bo’lib, yechim x2=− x1(1+x1)−1 dan iborat. Bu yechimni nol nuqtada Teylor qatoriga yoysak yuqorida topilgan qatorga kelamiz. 2.2 – §. Funksiyalarning kichiklik tartibi. Quyidagi ϕ(τ)=bτ P(1+0(1)) funksiyani qaraymiz. Bunda 0<τ< ρ , ρ>0 va 0(1) : τ→ 0 da 0(1)→ 0 shartni qanoatlantirsin, b va p haqiqiy sonlar bo’lib, b>0 bo’lsin. U holda p>0 da ϕ(τ)→ 0 p=0 da ϕ(τ)→ b p<0 da ϕ(τ)→ ∞ bo’ladi. Quyidagi ikkita funksiya berilgan bo’lsin, ϕ(τ)=bτ P(1+0(1)) (1) ϕ1(τ)=b1τP1(1+0(1)) (2) p>P1>0 bo’lganda |ϕ1|>|ϕ| bo’lib, τ ning yetarlicha kichik qiymatlarida bu funksiyalarning grafiklari 2 – 1 chizmadagi ko’rinishga ega bo’ladi. 13 1  2-1      1 0 2-2 Agar P=P1 va b1>b bo’lsa, |ϕ1|>|ϕ| bo’lib, grafiklar xuddi yuqoridagidek bo’ladi. Masalan: ϕ=1000 τP , ϕ1=τP1 da grafiklar bo’ladi. Lekin τ ning yetarlicha kichik qiymatlarida funksiyalarning joylashishi xuddi 2-1. rasmdagidek bo’ladi. P>P1>0 holda ϕ+ϕ1=b1τP1(1+0(1)) ϕ⋅ϕ1=bb 1τP+P1(1+0(1)) bo’ladi. Parametrni τ=cτ ¿α(1+0(1)) (3) almashtirganda (bunda c>0 va α>0 ), (1) funksiya ϕ¿(τ¿)=ϕ(τ)= bc Pτ¿Pα (1+0(1))= b¿τ¿P¿ (1+0(1)) 14 bo’lgan yana o’sha ko’rinishli funksiyaga o’tadi, faqat buning daraja ko’rsatkichi P¿= αP , koeffitsiyenti esa b¿= bc P bo’ladi. 2.3 – §. Tekis egri chiziqlarning kichiklik tartibi . x1x2 tekislikda quyidagi ikkita parametrik tenglamalar bilan berilgan F egri chiziqni qaraymiz F:¿{x1=b1τ P1(1+0(1))¿¿¿ (4) Parametrlar orqali ifodalanuvchi bunday egri chiziqlarni W sinflarning egri chiziqlari deb ataymiz. Bularni x1= x2= 0 , ya’ni nolning atrofida qaraymiz, demak, P1>0 va P2>0 bo’ladi. Qulaylik uchun b1 va b2>0 deb olish mumkin. 2 – 3 rasmda W sinfdagi qandaydir F egri chiziq ko’rsatilgan. P=(p1,p2) vektorni F egri chiziqning (vektorli) tartibi deymiz. Agar F egri chiziqda τ o’rniga yangi τ¿ parametr kiritilsa, (3) formulaga ko’ra biz F:¿{x1=b1c P1τ ¿P1 α (1+0(1))=b1 ¿ τ ¿P1 α (1+0(1))¿¿¿ (5) ni hosil qilamiz. Demak, τ¿ parametr bo’yicha F egri chiziq W sinfdagi egri chiziq bo’ladi, yangi parametrlarda vektorli tartib P¿= (p1 ¿,p2 ¿)=(αp 1,αp 2)=αP bo’ladi. Shu sababli F egri chiziqning (3) formulalar orqali aniqlanuvchi har xil parametrlanishida P¿ vektorli tartiblar mos kelib, ular Φ = {p ¿ :p ¿ = αP ,α> 0} nurda joylashgan bo’ladi. Masalan, 15 2x F~ F 1x 02-3 2-4 P p~ p 1pP 2p 0 F:¿{x1=τ¿¿¿ (6) egri chiziqning grafigi 2 – 3 rasmda tasvirlangan bo’lib, P=(1,3 ) tartib va tartiblar nuri Φ 2 – 4 rasmda tasvirlangan. (6) egri chiziq bitta x2= x13 tenglama bilan berilgan. Umuman, agar F egri chiziqda τ parametr sifatida x o’zgaruvchi olinsa, u holda vektorli tartib P dagi birinchi koordinata p1=1 bo’ladi. (4) egri chiziq bilan bir qatorda ~ F:¿{x1= ~ b1 ~τ ~P1(1+0(1))¿¿¿ (7) egri chiziqni ham qarab chiqamiz. x1x2 tekislikda F , ~F egri chiziqlarni (2 – 3) rasm, p1p2 tekislikda esa bu chiziqlarga mos tartiblar nurlari ρ va ~ρ larni qarab chiqamiz (2 – 4 rasm) Agar ρ nur ~ρ nurdan chaproqda joylashgan bo’lsa, u holda nolni yetarlicha kichik atrofida F egri chiziq ~F egri chiziqdan o’ngroqda joylashishini ko’rishimiz mumkin. Buni tushunish uchun ikki chiziqda ham parametr sifatida x1 ni olish yetarli. Masalan, F (6) formula bilan, ~F esa ~ F : ¿ { x 1= τ 2 ¿ ¿ ¿ 16 formula bilan berilgan bo’lsin. U holda ~P=(2;3) (2 – 3 va 2 – 4 rasmlarga qarang). Demak, x1x2 tekislikdagi nol nuqtaning kichik atrofi geometriyasi va p1p2 tartiblar tekisligi geometriyasi orasida aniq bir bog’lanish borligini ko’rishimiz mumkin. Egri chiziqlarning eng sodda ko’rinishini qaraymiz: x1=b1τP1 x2=b2τP2 Bunday egri chiziqlar W0 sinfga qarashli deymiz. Nolning yetarlicha kichik atrofida W sinfning har bir egri chizig’ini W0 sinflarning ikkita egri chiziqlari orasiga joylashtirish mumkin. W0 sinfning ikkita egri chizig’ini qaraymiz. F¿= {x1= b1τP1 x2=(b2+ε)τP2} F¿= {x1= b1τP1 x2=(b2− ε)τP2} Bularni (4) egri chiziq bilan solishtirsak, ular bir xil P=(p1,p2) tartibga ega ekanligini va faqat b2 , b2+ε , b2−ε koeffitsiyentlar bilan farq qilishini ko’ramiz. Bu o’zgarmaslarda ma’lum bir kichik o’zgarishlar bajarib F¿ va F¿ larni mos ravishda F egri chiziqning yuqorisida va pastida joylashtirish mumkin. 2.4 – §. Analitik funksiyalarning lokal xossalari . Ikki o’zgaruvchining funksiyasi f(x1,x2) berilgan bo’lsin. Soddalik uchun f(x1,x2)= ∑ j=1 m ajx1 q1jx2 q2j (9) deb faraz qilamiz, bunda qij - butun sonlar, aj - koeffitsiyentlar haqiqiy sonlar. 17 Faraz qilaylik biror (4) egri chiziq ham berilgan bo’lsin. F egri chiziqda f(x1,x2) funksiyaning o’zgarishini qaraymiz. f - birhad bo’lgan holni qarashdan boshlaymiz, ya’ni f= x1 q1x2 q2 bo’lsin. U holda f(τ)= fF= b1q1b2q2τp1q1+p2q2(1+0(1)) Bu funksiyaning τ bo’yicha tartibi p1q1+p2q2= (Q ,P) bo’lib, bunda (Q,P) - Q=(q1,q2) va P=(p1,p2) vektorlarning skalyar ko’paytmasini ifodalaydi. Endi umumiyroq holni, (9) ko’rinishdagi holni qaraymiz. U holda fF=∑j=1 m ajx1q1jx2q2jτq1jp1+q2jp2(1+0(1)) (10) Bu summaning daraja ko’rsatkichlari har xil j larda har xil bo’ladi va agar Qj=(q1j,q2j) deb belgilasak, u holda bu ko’rsatkichlarni (Q1,P) skalyar ko’paytma deb ifodalash mumkin. (10) summada kichik daraja ko’rsatkichli qo’shiluvchining qiymati katta bo’lganligi sababli shunday j indekslarni ajratamizki, ularda ko’rsatkich minimal qiymatni qabul qilsin: τ= min 1≤j≤m (Qj,P) , bunda P fiksirlangan. Faraz etaylik bu minimum aniq bir j= j1,j2,...js larda erishilsin, ya’ni (Qj,P)=r bo’lsin. U holda qolgan j≠ j1,j2,...js lar uchun (Qj,P)>r bo’ladi. Bu skalyar ko’paytma τ ga teng bo’lgan hadlarni ajratib olamiz, ya’ni yangi funksiyani kiritamiz. ~f(x1,x2)= ∑k=1 s a jkx1 q1jkx2 q2jk F egri chiziqda fF=~fF(1+0(1))=~f(b1,b2)τr(1+0(1)) . ~f funksiyaga, f funksiyaning P tartib bo’yicha birinchi yaqinlashishi yoki f ning P - tartib bo’yicha qisqartmasi deyiladi. Bunday konstruksiyada 18 F egri chiziqning faqat tartibi bilangina ish ko’rilyapti. ~f qisqartma F egri chiziqda f funksiyaning bosh hadini bergani uchun f dan birinchi yaqinlashishni ajrata olishni bilish kerak. shuni ta’kidlash kerakki, har xil P tartiblar uchun f ning ~f qisqartmalari ham har xil bo’ladi. Qisqartmalarni ajratish quyidagi masalaga olib keladi. Faraz etaylik bir nechta Qj , j=1,...,m vektorlar berilgan bo’lsin. Har bir P>0 vector uchun shunday j1,j2,...js indekslarni ajratish kerakki, bunda (Qjk,P)=(Qjs,P) k=1,...,s (Qj,P)>(Qjj,P) j≠ j1,j2,...js bo’lsin. Agar f funksiyaning ~f qisqartmasini faqat bitta P tartib bo’yicha topish kerak bo’lsa, (Qj,P) skalyar ko’paytmalarni bir qator qarab chiqib, ular ichidan eng kichigini olish lozim. Lekin biz P tartiblarning cheksiz to’plamidan barcha qisqartmalarni topishimiz kerak. bu masalani yechishda geometrik talqin etishdan foydalanamiz. Masalani ikkita geometrik usulda yechish yo’llari ma’lum: N’yuton ko’pburchagi va Frommer ko’pburchagi. N’yuton ko’pburchagi . Har bir Qj=(q1j1,q2j2) vektorga q1q2 tekislikdagi (q1j,q2j) nuqtani mos qo’yamiz. Bunday nuqtalar to’plamini D= D(f) bilan belgilaymiz. Fiksirlangan P vektorda (Q ,P)=r=const (11) tenglama q1q2 tekislikdagi P vektorga ortogonal to’g’ri chiziqni aniqlaydi. Agar p>0 bo’lsa, u holda τ ning oshishi bilan (11) to’g’ri chiziq chapga siljiydi. Agar D to’plamning har bir Qj nuqtasi orqali (Q ,P)=(Q j,P) to’g’ri chiziq o’tkazilsa, u holda (Q,P) skalyar ko’paytmaning eng kichik qiymati bu to’g’ri chiziqlarning eng chapdagisida bo’ladi. 19 Ba’zi bir geometrik tushunchalarni eslatamiz. D - q1q2 o’zgaruvchilarning R2 tekisligida nuqtali to’plam bo’lsin. Tayanch to’g’ri chiziq . D to’plamning P vektor bo’yicha lp tayanch to’g’ri chizig’i (Q ,P )= infQ∈D(Q ,P )= const tenglama bilan beriladi. Agar D chekli to’plam bo’lsa, u holda inf =min bo’ladi va tayanch to’g’ri chiziq quyidagi xossa bilan ajralib turadi: undan bir tomonda D to’plamning nuqtalari yo’q, lekin uning o’zida D ning nuqtalari bor. Shuni ta’kidlash lozimki, qisqartmalarni ajratish D to’plamning barcha p>0 uchun uning tayanch to’g’ri chiziqlar Lp bilan kesishmalarini topishga ekvivalentdir. Quyidagi (Q ,P )≥ infQ∈D(Q ,P )= const tengsizlik bilan aniqlangan ~l yarim tekislik tayanch yarim tekislik deyiladi. M bilan D to’plamning lp tayanch yarimtekisliklarining barcha P>0 vektorlar bo’yicha kesishmasini belgilaymiz: M = ¿P>0lP M to’plam qanday to’plam ekanligini tasavvur qilish uchun D to’plamning Qj nuqtalari chekli bo’lgan holni qaraymiz va q1q2 tekislikda barcha P≠0 vektorlar bo’yicha barcha tayanch yarimtekisliklar kesishmasi Γ ni aniqlaymiz (musbat va manfiy) Γ= ¿P≤0 ~lP Chiziqli tengsizliklar nazariyasida Γ qavariq ko’pburchak ekanligi va uni D to’plamning qavariq qobig’i sifatida hosil qilish mumkinligi isbotlanadi, ya’ni Γ={Q : Q=α1Q1+α2Q2+...+αnQn, αi≥0 ∑j=1 m αj=1} 20 )0,1(P )1,1(   P )0,1(P )0,1(P )0,1(P )0,1(P )0,1(P )0,1(P )0,1(P )1(1 )1(3 )1(2   5 2  Γ ko’pburchakning chegarasi chekli sondagi uchlar va qirralardan (yoki tomonlardan) tuzilgan. Uchlar D to’plamning nuqtalaridan iborat bo’ladi. D to’plamning uchlardan farqli boshqa nuqtalari Γ ko’pburchakning qirralarida va ichida joylashgan bo’lishi mumkin. Ba’zi qirralarda D to’plamning uchlardan boshqa nuqtalari bo’lmasligi ham mumkin. 1 – misol . f= x1+x2+x1x2 Bu yerda Q1=(1,0 ) , Q2=(0,1 ) , Q3=(1,1 ) (2 – 5 rasm) P=(1,1 ) uchun tayanch to’g’ri chiziq (Q,P)=1 (yoki (Q2,P)=1 , (Q3,P)=2>1 ) tenglama bilan beriladi, tayanch yarimtekislik q1+q2>1 . Xuddi shunday P=(1,0 ) uchun tayanch to’g’ri chiziq va tayanch yarimtekislik q1= 0 va q1≥0 tenglama bilan beriladi. Va P=(−1,−1) uchun tayanch to’g’ri chiziq va yarimtekislik −q1− q2=− 2 va −q1− q2≥− 2 bo’ladi. Bunda Γ ko’pburchak uchlari Q1, Q2, Q3 da bo’lgan uchburchak (2 – 5 rasmda gorizontal shtrixlangan) M ko’pburchak uchta q1≥0 , q2≥0 , q1+q2≥ 1 (2 – 5 rasmda vertikal chiziqlar bilan shtrixlangan) tengsizliklar yordamida quriladi. Γ ko’pburchakning uchlarini alohida, qirralarini alohida nomerlaymiz, va Γj(d) bilan belgilaymiz, d - ob’yektning o’lchami, (uchlar 21 uchun d=0 , qirralar uchun d=1 ) j indeks esa nomerni ifodalaydi. Umuman olganda uchlar va qirralarni ixtiyoriy ravishda nomerlash mumkin, lekin eng qulayi quyidagidan iborat. Biror uchni tanlaymiz va aylanib chiqish yo’nalishini belgilaymiz (masalan soat strelkasi harakati bo’ylab). Tanlangan uchni Γ1(0) bilan belgilaymiz, va belgilangan yo’nalish bo’yicha borganda keyingi uchraydiganini Γ2(0) , keyin Γ3(0) va h.k. belgilaymiz. Oxirda Γn(0) uchni topamiz, undan keyingisi Γ1(0) bo’ladi. So’ng uchalari Γj(0)−Γj+1(0) bo’lgan qirrani j<n bo’lganda Γj(1) bilan belgilaymiz va oxirida Γn(1) bilan Γn(0) va Γ1(0) uchlar orasidagi qirrani belgilaymiz. Yuqorida qarab chiqilgan misolda Γj(0)=Q j deb qirralarni esa xuddi 2 – 5 rasmdagi kabi nomerlash mumkin. Γj(0) uchlar ko’pburchakda alohida rol o’ynaydi. Birinchidan Γ ko’pburchak o’zining barcha uchlarining qavariq qobig’idan iborat, ikkinchidan, har bir Γj(1) qirra o’zining Γj(0) va Γj+1(0) uchlarining qavariq qobig’idan iborat. Dj(0) bilan D to’plamning Γj(d) uchi yoki qirrasi bilan kesishmasini belgilaymiz. D j(d)= D∩ Γ j(d) Γ ko’pburchakning uchlari D to’plamning nuqtalari bo’lganligi uchun D j(0)=Γj(0) bo’ladi. D to’plamga Γj(1) qirrani chegaralovchi Γj(0) va Γj+1(0) uchlari va shu qirrada yotuvchi D ning nuqtalari qarashli bo’ladi. Yuqorida qaralgan misolda D j(0)=Q j j=1,2,3 . D1(1)=(Q1,Q2) , D2(1)=(Q2,Q3) , D3(1)=(Q3,Q1) Har bir tayanch to’g’ri chiziq Γ ko’pburchak bilan yoki qirra bo’yicha, yoki uchlar bo’yicha kesishishini qayd etamiz. Teskarisi ham o’rinli: har bir 22 qirra yoki uch ko’pburchak bilan biror tayanch to’g’ri chiziq kesishishidan hosil bo’ladi. Shunday qilib, D to’plamning uning tayanch to’g’ri chizig’ining kesishmasi albatta Dj(d) lardan birortasi bo’lib, u Γ ko’pburchakning qirrasi yoki uchlarida yotadi. Shu sababli tayanch to’g’ri chiziqlarning D to’plam bilan kesishmasini (ya’ni Dj(d) to’plamlarni) o’rganish Γ ko’pburchakning uchlari va qirralarini o’rganishga teng kuchlidir. Agar Γ j(d)= Lp∩ Γ va ~Q∈Lp bo’lsa, u holda (Q,P)=(~Q,P) , barcha Q∈Γj(d) da. (Q ,P)>(~Q ,P) , barcha Q ∈ Γ ¿j(d) larda. Xususiy holda D nuqta va Dj(d) to’plamlar uchun xuddi yuqoridagidek (Q,P)=(~Q ,P) , barcha Q ∈Dj(d) da. (Q ,P)>(~Q ,P) , barcha Q ∈ D ¿j(d) da munosabatlarga ega bo’lamiz. Qisqartmalar konuslari . Teskari masalani qaraymiz. Faraz etaylik, Γj(d) - Γ ko’pburchakning qandaydir qirrasi yoki uchi bo’lsin. Barcha shunday P vektorlar to’plamini topish kerakki, ular uchun Γ j(d)= Lp∩ Γ bo’lsin, ya’ni Lp tayanch to’g’ri chiziq Γ ko’pburchak bilan faqat Γj(d) lar bo’yichagina kesishsin. Bunday P vektorlar to’plamini Γj(d) uchning yoki qirraning konusi deymiz va Kj(d) bilan belgilaymiz. Shunday qilib, K j( d )= ¿ ¿ ~Q∈Γj (d) bo’lsin. Kj(d) konusning P vektorlari quyidagi tengliklar va tengsizliklar sistemalari orqali aniqlanishi ravshan: barcha, Q∈Γj(d) larda (Q,P)=(~Q ,P) barcha, Q ∈ Γ ¿j(d) larda (Q ,P)>(~Q ,P) . 23 Bu shartlardan birinchisi shuni ko’rsatadiki, (Q,P)=(~Q,P) to’g’ri chiziq Γj(d) to’plamni o’zida saqlaydi: ikkinchi shart bo’lsa, bu to’g’ri chiziq Γ ko’pburchak uchun tayanch to’g’ri chiziq ekanligini ko’rsatadi. Γ ko’pburchak D to’plam nuqtalarining qavariq qobig’i, Γj(d) bo’lsa Dj(d) to’plamning qavariq qobig’i bo’lganligi sababli, Kj(d) konusni berishda faqatgina D ning nuqtalarini berish yetarli ya’ni biror ~Q ∈D j (d) uchun K j(d)={P:(Q ,P)=(~Q ,P) barcha Q ∈D j(d)da (Q ,P)>(~Q ,P) barcha Q ∈D ¿j(d) } 1 – misol . (2.1 paragrafdagi 1 – misolning davomi). Qarab chiqilgan f= x1+x2+x1x2 misolda, Γ1(1) qirra uchun K j(d)={P:(Q1,P)=(Q2,P) (Q3,P)>(Q1,P) ga ega bo’lamiz. Qj nuqtalarning sonli qiymatlarni hisobga olsak, K1(1)= {P :p1= p2 p1+ p2> p1} yoki K 1(1)= {P :p 1= p 2> 0 } p1,p2 tekislikda K1(1) konus birinchi kvadrantning bissektrisasi bo’lgan nurdan iborat bo’ladi. (3 – 1 rasm). Bu nur Γ1(1) qirraga perpendikulyar bo’lib, Γ1(1) qirrada yotmaydigan Q3 nuqtaga tomon yo’nalgan. Xuddi shunday K2 (1)={P:(Q2,P)=(Q1,P) (Q1,P)=(Q2,P)}={P:p1=0, p2<0} ni topamiz. p1,p2 tekislikda K2(1) konus Γ2(1) qirraga ortogonal bo’lgan nurdan iborat. Nihoyat 24 K3 (1)={P:(Q2,P)=(Q1,P) (Q2,P)>(Q1,P)}={P:p1<0, p2= 0}ham nur bo’ladi. (3 – 1 rasmni qarang) Endi uchlarning konuslarini topamiz. Γj(0) uch D to’plamning yagona nuqtasini saqlaganligi uchun konus ta’rifidagi tengliklar ma’nosini yo’qotadi, faqat tengsizliklar qoladi. Shunday qilib K1(0)={P:(Q2,P)>(Q1,P) (Q3,P)>(Q1,P)} Qj nuqtalarning sonli qiymatlarini hisobga olsak K1(0)= {P:p2>p1 p1+ p2> p1}= {P:p2> p1 p2>0} p1,p2 tekislikda K1(0) - K1(1) va K2(1) (3 – 1 rasm) nurlar bilan chegaralangan burchak. Xuddi shunday K2(0)={P:(Q1,P)>(Q2,P) (Q3,P)>(Q2,P)}={P:p1>p2 p1>0} ni topamiz, u K1(1) va K2(1) nurlar bilan chegaralangan burchakdir. K3(0)={P:(Q1,P)>(Q3,P) (Q2,P)>(Q3,P)}={P<0} esa K2(1) va K3(1) nurlar bilan chegaralangan burchakdir. Taxlil qilgan misolda konus: Kj(d) ancha sodda berildi, bu D to’plamning sodda tuzilishidan bog’liqdir (u faqat uchta nuqtadan iborat). Umumiy holda konusning berilishidagi tenglik va tengsizliklar sonini qisqartirish mumkin, bunda D ning barcha nuqtalari o’rniga Γ ko’pburchakning faqat Γj(0) uchlarini qarash yetarli. U holda 25 K j(1)={P:(Γk(0),P)=(Γj(0),P) Γ j(0)иΓ k(0)∈Γj(1) (Γi(0),P)>(Γ j(0),P) Γi(0)иΓ ¿j(1) } K j(0)={P:(Γi(0),P)>(Γ j(0),P) Γi(0)≠ Γ j(1)}Bundan tashqari Kj(1) ning ta’rifida faqat bitta tengsizlikni qoldirish yetarli, chunki tenglik Γj(1) qirraga ortogonal bo’lgan to’g’ri chiziqni ifodalaydi, har bir tengsizlik bo’lsa, bu to’g’ri chiziqdan Γ ko’pburchakning ichi tomon yo’nalgan yarim to’g’ri chiziqni ajratadi. Kj(0) uchning konusi ta’rifida faqat ikkita tengsizlikni qoldirish yetarli: K j(0)={P:(Γj−1 (0),P)>(Γj(0),P) (Γj+1(0),P)>(Γj(0),P)} ya’ni Γj(0) uchning konusi Γj(0) uchga yopishgan Γj−1(0) va Γj(1) tomonlarning normallari bilan chegaralangan. Bu Kj(0) konusning berilishidagi tengsizlikni (Γi(0)−Γ j(0),P)>0 ko’rinishda yozish mumkinligidan kelib chiqadi. Bularning hammasi (Γ1(0)−Γ j(0),P)>0 (Γj+1(0)− Γj(0),P)>0 tengsizliklardan kelib chiqadi, chunki Γj−1(0)−Γj(0) vektorlar ikkita Γj−1(0)−Γi(0) va Γj+1(0)−Γj(0) vektorlar hosil qilgan burchakning ichida yotadi, ya’ni Γi(0)−Γj(0)=c1(Γj−1 (0)−Γj(0))+c2(Γj+1(0)− Γj(0)) bunda c1,c2>0 Shuni ta’kidlash kerakki, Q va P vektorlar mos ravishda R2 va ¯R2 qo’shma tekisliklarga tegishli. 2 – misol . f= x13+x23−3x1x2+x1x22 Bunda Q1=(3,0 ) Q2=(0,3 ) Q3=(1,1 ) Q4=(1,2 ) (3 – 2 rasm) 26 Q1, Q2 , Q3 nuqtalar uchlardan iborat. Γ1(0)=Q1, Γ2(0)= Q2, Γ3(0)=Q3 belgilaymiz. U holda - Q1 va Q3 uchli qirra. Γ2(1) - Q3 va Q2 uchli qirra; Γ3(1) - Q2 va Q1 uchli qirra. Dj(d) to’plam D1(0)=Q1, D2(0)=Q2, D3(0)=Q3 D1(1)= Q 1∪ Q 3 D 2(1)= Q3∪ Q2, D3(1)= Q2∪ Q 4∪ Q1 Bularga f funksiyaning oltita qisqatrmasi mos keladi: ^f1(0)= x13 , ^f2(0)=−3x1x2 , ^f3 (0)= x2 3 , ^f1(1)=x13−3x1x2 , ^f2(1)=x23−3x1x2 , ^f3(1)= x13+x23+x1x22 Endi K j( 1 ) konuslarni topamiz. (ularni biz fj(d) qisqartmalarning konuslari deb ataymiz) u holda 27 )1(1 K 1( 1) = { P : ( Γ 1 ( 0) , P ) = ( Γ 2 ( 0) , P ) < ( Γ 3 ( 0) , P )} = { P : p 2 = 2 p 1 > 0 } K 2 ( 1) = { P : ( Γ 2 ( 0) , P ) = ( Γ 3 ( 0) , P ) < ( Γ 1 ( 0) , P )} = { P : 2 p 2 = p 1 > 0 } K 3 ( 1) = { P : ( Γ 3 ( 0) , P ) = ( Γ 1 ( 0) , P ) < ( Γ 2 ( 0) , P )} = { P : p 1 = p 2 < 0 } K 1 ( 0) = { P : ( Γ 3 ( 0) , P ) > ( Γ 1 ( 0) , P ) ,( Γ 2 ( 0) , P ) > ( Γ 1 ( 0) , P )} = { P : p 2 > p 1 , p 2 > 2 p 1 } K2(0)={P:(Γ1(0),P)>(Γ2(0),P),(Γ3(0),P)>(Γ2(0),P)}= {P:2p1>p2,2p2>p1} K 3 ( 0) = { P : ( Γ 2 ( 0) , P ) > ( Γ 3 ( 0) , P ) ,( Γ 1 ( 0) , P ) > ( Γ 3 ( 0) , P )} = { P : p 1 > 2 p 2 , p 2 < p 1 } Maxsus hol (buzilgan hol) D to`plamning barcha nuqtalari bitta to`g`ri chiziqda yotib qolishi ham mumkin. Bu holda ko`pburchak kesma ko`rinishini oladi va faqat bitta Г 1( 1 ) = Г qirraga, ikkita Г 1( 0 ) va Г2(0) uchga ega bo`ladi. Masalan, f= x12+x22+x1x2 . Bu holda Q1= (2,0 ),Q2=(0,2 ),Q3=(1,1 ) Г ko`pburchak uchlari Г 1( 1 ) = Q 1 va Г 2( 1 ) = Q 2 da bo`lgan kesmadan iborat bo`ladi. Uchta to`plamga ega bo`lamiz 28 D j( d ) : D 1( 0 ) = Q 1 , D 2( 0 ) = Q 2 , D 1( 1 ) = D = Q 1 ∪ Q 2 ∪ Q 3 va bularga muvofiq ravishda ^f1(0)= x12 , ^f2(0)= x22 , ^f1(1)= f qisqartma konuslar berilishida umumiy holga qaraganda bitta tengsizlik kamayadi. Shunday qilib K 1( 1 ) = { P : ( Γ 1 ( 0) , P ) = ( Γ 2 ( 0) , P )} = { P : p 1 , p 2 } bu to’liq to’g’ri chiziqdan iborat (maxsus holdagi kabi yarim to’g’ri chiziq emas) K 1( 0 ) = { P : ( Γ 2 ( 0) , P ) > ( Γ 1 ( 0) , P )} = { P : p 2 > p 1 } K 2( 0 ) = { P : ( Γ 1 ( 0) , P ) > ( Γ 2 ( 0) , P )} = { P : p 1 > p 2 } Bu masalada f - bir jinsli ko`p h ad ekanligiga e`tibor beramiz. Umuman olganda, ixtiyoriy bir jinsli f ko`phadli uchu n D ( f ) to`plamning nuqtalari bitta to`g`ri chiziqda yotadi. Aksincha, agar D ( f ) ning nuqtalari bitta to`g`ri chiziqda yotsa, u holda ko`p h ad kvazibirjinsli bo`ladi. f = a x 1q 1 x 2q 2 bir hadli uchun bo`lsa, D toplam faqat bitta Q1 nuqtadan iborat bo`ladi. Shuning uchun Г ko`pburchak yagona uchdan iborat bo`lgan shu Q1 nuqtadan iborat bo`lib qoladi. Demak, Г = Г 1( 0 ) = Q 1 , D = D 1( 0 ) ¿ Q 1 va demak, faqat bitta ^ f = f qisqartmadan iborat bo`ladi. K 1( 0 ) konus bu t un p1p2 tekislikdan iborat bo`ladi, chunki P vektorga hech qanday shart qo`yilmaydi. 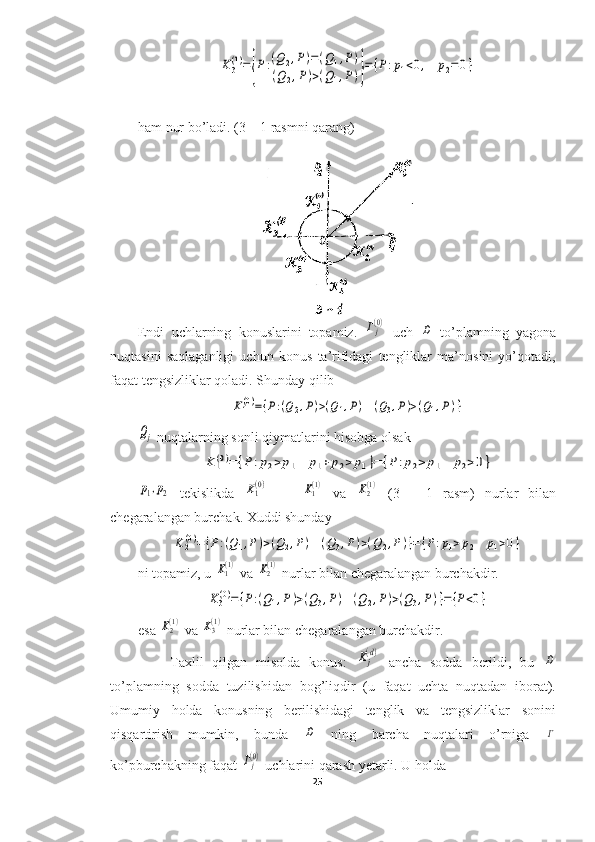1-misol. n = 2 bo'lsin va S to'plam uchta nuqtadan iborat bo’lsin. S = { Q 1 = ( 3 , 0 ) , Q 2 = ( 0 , 3 ) , Q 3 = ( 1 , 1 ) } . Qavariq qobiq G bu uchlari va R2 tekisligidagi uchta qirrali G j( 1 ) uchburchakdir G j( 0 ) = ¿ Q j , j =1,2,3, ( 3.1-rasm). Edge G j( 1 ) = ¿ [ Q 1 , Q 3 ], uning yo'nalishi vektori R 1 = Q 3 - Q 1 = (2 , - 1) . Oddiy vektor N 1 = (1 , 2) . Lekin bu vector N 1 chetidan G 1( 1 ) uchburchakka yo'naltirilgan G . Shuning 29 uchun tashqi normal N 1 = (-1 , - 2) . Uning ustidan λ > 0 bo lgan λʻ N 1 = (− λ , − 2 λ ) nur normal konusdir U 1( 1 ) . U 2( 1 ) = λ ( − 2 , − 1 ) va U 3( 1 ) = λ (1, 1), λ ¿0 ni xuddi shu tarzda topamiz . Oddiy tepa konus G 1( 0 ) = Q 1 mavjud U 1( 0 ) ={P= λ ( − 1 , − 2 ) + µ (1, 1), λ , µ > 0 } Xuddi shunday, biz oddiy konuslarni topamiz: U 2(0)=¿ {P= λ ( − 2 , − 1 ) + µ (1, 1), λ , µ > 0 } U 3( 0 ) = ¿ {P= λ ( − 1 , − 2 ) + µ (-2, -1), λ , µ > 0 } 3.2 rasm Dekart yaprog’ining tayanchi va Nyuton ko’pburchagi (2.2). Ular rasmda ko'rsatilgan. 3.2. Shunday qilib, konjugat tekislikda R¿2 qirralarga normal va G j(1) G uchburchakdan tashqariga yo'naltirilgan nurlar normal konuslarni U j(1) qirralarini hosil qiladi. G j( 1 ) (3.2-rasm). Ularning orasidagi sektorlar oddiy konuslar U j( 0 ) uchlari G j(1) 30 3.1-misol. To‘rt nuqtadan tashkil topgan S to‘plamning qavariq qobiqi G chegarasini hisoblang Q 1 = (3 , 0) , Q 2 = (0 , 3) , Q 3 = (1 , 1) , Q 4 = (2 , 2 ) , va normal konuslari U j( d ) uning ob'ektlari G j(1) . Natijalarni ikkita rasmda ko'rsating. ∂ G emas, balki uning faqat R yo'nalishlarining ma'lum bir K to'plamiga mos keladigan qismi qiziqtiradi. Keyin K to'plamini masala konusi deb ataymiz . Bu konveks bo'lishi shart emas. ∂ G (K) chegaraning ∂ G qismining elementlari uchun G j( d ) ularning normal konuslari U j( d ) masala konusi K bilan kesishgan qismini belgilaymiz . 3.2-misol. n = 2 va K 1 yuqori yarim tekislik K 1 = { P = ( p 1 , p 2 ) : p 2 > 0} , K 2 o‘ng yarim tekislik K 2 = { P = ( p 1 , p 2 ) : p 1 > 0} va K 3 uchinchi kvadrant K 3 ={ P =( p 1 ,p 2 ) < 0} , keyin ∂ G (K) yuqori. 3.2. Ko'pburchak yuzlarining G j( d ) oddiy konuslari U j( d ) 3.1-rasm chegaraning bir qismi ∂ G , ∂ G (K 2 ) chegaraning o'ng qismi ∂ G va ∂ G (K 3 ) chegaraning chap va pastki qismlarining kesishishi ∂ G . Oddiy konusning barcha vektorlari U j( d ) yuzga G j( d ) ortogonaldir. Oddiy konuslarning bir jinsliligi tufayli ularning ikkita gipertekislik bilan kesishgan joylarini (masalan, p n = ±1 ) ko'rib chiqish va ulardagi kesishmalarni belgilash kifoya. 31 III bob TEKIS ALGEBRAIK CHIZIQLARNI ULARNING KO’PYOQLIKLARI YORDAMIDA TADQIQ QILISH 3.1. Oddiy nuqtaning lokal tahlili. II-bobda kiritilgan f(x1,x2) – funksiya haqiqiy yoki kompleks koeffisiyentli ko'phad bo'lsin. Quyidagi f(x1,x2)=0 (3.1) tenglamaning yechimlar i to’plami ga F = {( x 1 , x 2 ) ∈ R 2 | f ( x 1 , x 2 ) = 0 } ,( F = {( x 1 , x 2 ) ∈ C 2 | f ( x 1 , x 2 ) = 0 }) yassi (tekis ) algebraik egri chiziq deb ataladi. Ma’lumki, x=(x10,x20) nuqtada f(x10,x20)= 0 bo’lib, bu nuqtada ( ∂ f ∂ x 1 , ∂ f ∂ x 2 ) ≠ 0 bo’lsa, x=(x10,x20) nuqta F - egri chiziqning oddiy nuqtasi deyiladi . Aks holda x=(x10,x20) nuqta (1) chiziqning maxsus yoki kritik nuqtasi deb yuritiladi. Koordinatalar sistemasiga siljitish almashtirishini qo’llab, koordinatalar boshini x=(x10,x20) nuqtaga o’tkazamiz. x=(x10,x20) nuqta (1) chiziqning oddiy nuqtasi bo’lganda quyidagi teorema o’rinli. 32 / 1 –teorema (Koshi [8]) . Agar x = ( 0 , 0 ) bo’lganda ∂ f ∂ x 2 ≠ 0 bo’lsa , u holda (1) tenglamaning barcha yechimlari x = ( 0 , 0 ) nuqta atrofida x 2 = ∑ k = 1∞ b k x 1 k yoyilmadan iborat bo’ladi, bu yerda b k — o’zgarmaslar (haqiqiy yoki kompleks). x=(x10,x20) nuqta (1) chiziqning maxsus nuqtasi bo’lganda yuqoridagi teorema o’rinli emas. Ushbu ishda maxsus nuqta atrofida (1) tenglamaninig taqribiy yechimlarini topish uchun darajali geometriya metodlaridan Nyuton ko’pyoqligi usuli qo’llanilgan [2], ma’lum bir yassichiziqning maxsus nuqta atrofidagi taqribiy yechimlari topilgan . f(x) ko’phadni quyidagicha tasvirlab olamiz: f(x)= ∑ aQxQ , ( 3 . 2 ) bu yerda x=(x1,x2) , Q = ( q 1 , q 2 ) , x Q = x 1q 1 x 2q 2 ,aQ-o’zgarmaslar koeffisiyentlar . (2) ko’phadga quyidagi to’plamni mos qo’yamiz. S ( f ) = { Q ∈ R 2 | a Q ≠ 0 }. S to’plam f ( x ) ko’phadning tashuvchisi deyiladi. Bu to’plam Q1...,Qk nuqtalardan iborat bo’lsin. S ( f ) t a s h u v c h i n i n g qavariq qobig’i G ( S ) = { Q = ∑ j = 1k µ j Q j , µ j ≥ 0 , ∑ j = 1k µ j = 1 } = N ( f ) to’plamdan iborat bo’lib, bu to’plamga f(x) ko’phadning Nyuton ko’pyoqligi deyiladi. B u k o ’ p y o q l i k n i n g c h e g a r a s i ∂ N ( f ) to’plam G j( 0 ) uchlar va G j( 1 ) qirralardan iborat, b u yerda j — qirra yoki uchning tartib raqamidan iborat. Har bir ummumlashgan G j( d ) qirraga uning chegaraviy qism to’plami S j( d ) = S ∩ G j( d ) mos keladi, bu qism to’plamga f(x) ning qisqartirilgan ko’phadi ^ f j( d)( x ) = ∑ a Q x Q , Q ∈ S j (d) mos keladi va bu qisqartirilgan ko’phadga o’zining normal konusi U j (d) = { P : ⟨ P , Q 1 ⟩ = ⟨ P , Q 2 ⟩ > ⟨ P , Q 3 ⟩ , Q 1 , Q 2 ∈ G j ( d) , Q 3 ∈ G ∖ G j (d)} mos keladi, bu yerda P = ( p 1 , p 2 ) ∈ R ¿2 , R¿2 tekislik R2 tekislikka qo’shma tekislikdan iborat. Endi x 1 ∈ C , x 1 → 0 yoki x1→ ∞ bo’lsin, o ( 1 ) - esa x 1 ning funksiyasidan iborat 33 → → ∞ bo’lib, u nolga intilsin. U holda x2=bx1p(1+o(1)), (bu yerda b∈C ,p∈R¿ egri chiziqda f q 1 q 2 x 1 q 1 x 2q 2 = f Q x Q , (3.3) (bu yerda Q=(q1,q2)xQ= x1q1x2q2,fQ∈C ,x∈C2) (3.3) monom fQbq2x1q1+q2(1+o(1))= fQbq2{exp [(q1++pq2)ln x1]}(1+o(1))= fQbq2{exp ¿ qiymatlar qabul qiladi. P = (1,p), | fQXQ | = | fQbq2 | { exp[ ⟨ Q , P ⟩ ω ∨ ¿ ln| x 1 ||]}(1+o(1)) ω = sgnln ∨ x 1 ∨ ¿ ={ Bu P v a ω larda eng katta modullarga shunday (3) monomlarda erishadiki ularda (3.2) yig’indilar ω ⟨Q ,P⟩bunda Q ∈ S (3.4) miqdor maksimumga erishadi. Agar x1 → 0 bo’lsa , u holda ω = − 1 v a vektor ω P = (-1 ,- p ) . Shuning uchun, bu erda masalaning konusi K- b u R 2 tekislikning chap yarim tekisligi va Q nuqtalar (4) maksimal qiymatlar bilan ∂N chegaraning chap qismida yotadi. Agar x1 → ∞ bo’lsa , u holda ω = 1 v a vektor ω P = (1 , p ) . Shuning uchun, bu erda masalaning konusi K- b u R 2 tekislikning o’ng yarim tekisligi va Q nuqtalar (4) maksimal qiymatlar bilan ∂N chegaraning o’ng qismida yotadi. f(X)= ∑Q∈S fQXQ=0 (3.5) tenglama yechimlarini x2=b1x1p1+b2x1p2+b3x1p3+… , (3.6) yoyilmalar ko’rinishida izlaymiz, bu yerda fQ , b k = const  C, Q  R 2 , p k = const  R ,  p k >  p k +1 . bilan birga o’sadi , agar x1 → 0 b Bu yoyilmalarda p k daraja ko’rsatkichlari k 34 -1 agar x 1 → 0 1 agar x2→ ∞ o’lsa, kamayadi, agar x 1 → ∞ bo’lsa, q uy i d ag i t e or e m a isbotlandi 2-t eorema. (3.5) tenglama (3.6) yechimlari uchun x2=b1x1p1 ( 3 . 7 ) qisqartirilgan yechim ω ( 1 , p 1 ) tashqi normal vektorli G j( d ) chegara elementiga mos f j ( d)( X ) = 0 (3.8) qisqartirilgan tenglamaning yechimi bo’ladi. Endi e'tibor bering, tegishli uchga mos (3.5) qisqartirilgan tenglamaning chap tomoni bitta monomialdan (3.3) iborat. Bunday qisqartirilgan tenglama faqat nol ildizga ega va (3.7). birinchi yaqinlashishni bermaydi Shuning uchun 3.2-teorema faqat qirralarga ya'ni d = 1 ga mos qisqartirilgan (3.8) tenglamalarga taalluqlidir. 3.1-misol . f= x13+x23−3x1x2 (3.9) bo’lsin . Tashuvchi uch nuqtadan iborat Q 1 = (3; 0); Q 2 = (0; 3); Q 3 = (1; 1) (3.1-misol). Ularning qavariq qobig’i bu uchlarga ega bo’lgan N uchburchakdir (3.1- rasm). Uning mos ravishda tashqi normallari −(2;1); −(1;2); (1;1) bo’lgan uchta qirrasi G1(1) , G 2( 1 ) va G3(1) bor.. Qisqartirilgan tenglama f~ 1 (1) = x1 3 − 3 x 1 x 2 = 0 x2= 1 3x 1 2 (3.10) yechimga ega. Qisqartirilgan tenglama f~ 2( 1) = x2 3 − 3 x 1 x 2 = 0 x 2 = ± √ 3 x 1 (3.11) yechimga ega. 35 (3.10) va (3.11) tarmoqlar x 1 = x 2 = 0; nolning atrofiga taaluqli; G 1( 1 ) , G2(1) qirralarga mos keladigan tashqi normallarining ikkala koordinatalari manfiy bo‘lgani uchun, nihoyat qisqartirilgan tenglama f 3( 1 ) = x 13 + x 23 = ( x 1 + x 2 ) ( x 1 2 − x 1 x 2 + x 22 ) x3 faqat bitta x2=− x1 (3.12) haqiqiy yechimga ega. Bu cheksizlikning x1= x2=∞ qo'shatrofiga taaluqli, chunki G 3( 1 ) qirraga mos keladigan tashqi normalining ikkala koordinatasi ham musbat. (3.9) egri chiziqning (3.10) – (3.12) qismlari 3.1. - rasmda ko'rsatilgan. Qisqartirilgan (3.8) tenglamadan foydalanib, ω ning ishorasi va p 1 daraja ko'rsatkichi bir qiymatli aniqlanadi: Agar (3.2) yig'indiida Q = (q 1 ; q 2 ) darajaning barcha vektor ko'rsatkichlari q 1 va q 2 ratsional komponentlarga ega bo'lsa, u holda p 1 ko'rsatkichi ratsionaldir. b 1 koeffitsienti uchun f j (1)( 1 , b 1 ) = 0 (3.13) algebraik tenglamani olamiz Biz ikkita holni ajratamiz: a) b 1 - (3.13) tenglamaning oddiy ildizi, u holda f j (1) x 2 ( 1 , b 1 ) ≠ 0; 36 3.1-rasm. Nol va cheksizlik yaqinida Dekart yaprog’i tarmoqlari bo’laklari. b) b 1 - (3.13) tenglamaning karrali ildizi, u holda f j(1) x 2 ( 1 , b 1 ) = ¿ 0; (3.5) tenglama yechimining (3.6) yoyilmasining b2x1p2 ikkinchi hadini hisoblash uchun x2= x1p1(b1+y2) (3.14) almashtirishni amalga oshiramiz. U holda (3.5) tenglama f( x1,x2 )= x1r¿ ], ko’rinishni oladi, bu yerda: r = ⟨( 1 , p 1 ) , Q ⟩ c Q ∈ Sj(1), g( y 1 , y 2 ) = ∑ gQ'YQ' shunga o’xshash Q'=(q1',q2') , ω q1'<0 Agar dastlabki (3.5) tenglamada barcha Q = (q 1 ; q 2 ) darajalar butun sonlar bo'lsa, u holda p 1 - maxraji s bo'lgan ratsional sondir. U holda a)  = −1 da g( y1,y2 )= x1−rf(x1,x2)= 0 37 tenglamaga, bu erda y 1 = x 1 1 s , 3.1-teorema qo'llaniladi, u umumiy s maxrajga ega p k ratsional ko'rsatkichli (3.6)yoyilmani beradi. Xuddi shunday a)  = −1 da y 1 = x 1 − 1 s uchun 3.1 teorema amal qiladi. b) holda (3.14) almashtirilgandan so'ng f( x 1 , x 1 p 1 ( b 1 + y 1 ) ) x 1− r =0 tenglama uchun yana Nyuton ko'pburchagini qurishimiz kerak;uning qirralarini topish lozim ng va hokazo. Agar biror k qadamda (3.13) ko'rinishdagi Qisqartirilgan tenglamaning oddiy b k ildiziga kelsak, u holda 3.1 teorema bo'yicha (3.5) dastlabki tenglama yechimning darajali yoyilmasini (3.6) ni olamiz. Agar har bir qadamda biz faqat karrali b k yechimni olsak, u holda f(X) ko'phadni har qanday kompyuter algebra tizimida mavjud bo'lgan kopaytuvchilarga yoyosh algoritmlaridan foydalanib f l (X) keltirilmaydigan polinom ko’paytuvchilarga yoyish kerak: f = f 1( X ) … f m ( X ) , (3.15) [17, § 53], [21, III qism, 6-band]. Har bir f l (X) ko’paytuvchida barcha tarmoqlar oddiy va (3.6) ko'rinishga ega. Aks holda, f l ( X ) va f l ( X ) x 2 ko'phadlari umumiy polinom ko’paytuvchia ega bo'ladi. Shunday qilib, 3.3- teorema . (3.5) polinom tenglama uchun barcha x 2 (x 1 ) yechimlari (5.6) ko rinishdagi qatorga yoyiladi, bunda barcha p ʻ k ko rsatkichlar umumiy maxrajli ʻ ratsional sonlardir. X = 0 nuqtaning atrofi uchun 3.3-teorema- bu V. Puiseux teoremasi, 1850 [22], ya'ni K = {P = (p 1 ; p 2 ) : p 1 ; p 2 < 0} masala konusi uchun.  N chegarasining mos qismi (pastki chap) Nyutonning siniq chizig'i deyiladi. 3.1 teoremasining yoyilmalari yaqinlashadi (qarang [23, § 184]), shuning uchun (3.5) polinom tenglamalar yechimlari uchun (3.6).barcha yoyilmalar yaqinlashadi 3.2-misol (3.1-misolning davomi). G1(1) qirra holida 38 x 2 = x 12 ( 1 3 + y 2 ) almashtirishdan so'ng f= x 13 + x 16( 1 3 + y 2 ) − − 3 x 13 ( 1 3 + y 2 ) = x 13 ( − 3 y 2 + 1 9 x 1 3 + … ) ni olamiz Qavslar ichida qisqartirilgan tenglama -3y 2 + x 13 /9 = 0. Bundan y 2 = x 13 / 27 kelib chiqadi. x 2 = 1 3 x 12 + 1 27 x 15 + … (3.16) G 2( 1 ) qirra holida x2=√x1(±√3+y2) almashtirishdan so'ng f= x 13 + x 1 3 2 ( ± √ 3 + y 2 ) 3 − 3 x 1 3 2 ( ± √ 3 + y 2 ) = x 1 3 2 ( x 1 3 2 + 9 y 2 + … − 3 y 2 ) Qavslar ichidagi qisqartirilgan tenglama x 1 3/2 1 + 6y 2 = 0; ya'ni y 2 = - x 1 3/2 /6. Shunday qilib, x 2 = ± √ 3 x 1 − 1 6 x 1 2 + … (3.17) Nihoyat, G 3( 1 ) qirra uchun (3.12) qisqartirilgan tenglama uchun D(1) x 2 = x 1 (−1 + y 2 ) ni (3.9) ga qo’gandan so'ng f= x 13 + x 13 ( − 1 + y 2 ) 3 − 3 x 12 ( − 1 + y 2 ) = x 13 ( 3 y 2 − 3 y 22 + y 23 ) + 3 x 12 − 3 x 12 y 2 (3.18) hosil bo'ladi. Ushbu ko'phadning tashuvchisi va ko'pburchagii 3.2. - rasmda ko'rsatilgan. Bu yerda x 1 → ∞ 1, 39 3.2-rasm. (3.18) ko'phadning tashuvchisi va Nyuton ko'pburchagi y 2→ 0, shuning uchun masala konusi K = {P : p 1 > 0 p 2 < 0}, ya'ni ko'pburchak chegarasining pastki o'ng qismini hisobga qarash kerak. U erda qisqartirilgan tenglamaga ega faqat bitta ~ G 1( 1 ) qirra mavjud 3x 2 1 + 3x 3 1 y 2 = 0: Uning yechimi y 2 = -1/ x 1 . Shunday qilib, bu erda x 2 = − x 1 − 1 + .. . (3.19) va yoyilma x 1 ning kamayuvchi darajalari bo’yicha davom etadi. x 2 = − x 1 − 1 (3.20) to’g’ri chiziq - bu cheksizlikka boradigan tarmoqlarning asimptotasi. Bu erda, barcha holatlarda, birinchi yaqinlashishlar oddiy ildizlarga ega bo'lib, ular egri chiziqning bir tarmog'iga mos keladi. 3.2. Haqiqiy egri chiziqning eskizi. f(X) ko’phadning barcha koeffitsientlari haqiqiy bo’lsin, u holda X  R 2 haqiqiy tekislikda yuqorida bayon qilingan lokal analiz yordamida uning barcha tarmoqlarini chizishimiz mumkin. Ushbu protsedurani bir necha bosqichlarga ajratamiz. 1-qadam. Yuqoridagi algoritmlar yordamida f(X) ko‘phadni (3.15) ko‘phadli ko\ 40 paytuvchilarga yoyamiz. Keyinchalik, har bir ajralmaydigan ko’paytuvchi f l (X) uchun alohida egri chiziqlar chizmalarini yasaymiz. 2-qadam.Yo\qotish usulidan foydalanib f = 0 egri chizig'ining f(X0 )=0, f x 1 ( X 0 ) =0, f x 2 ( X 0 ) = 0 , o\rinli bo’lgan barcha haqiqiy chekli kritik (maxsus) X 0 nuqtalarini topamiz, 3-qadam. Har bir X 0 maxsus nuqta yaqinida uni koordinata boshiga o'tkazib 3 va 3.2 bo'limlar usullaridan foydalanib biz (3.6) ko’rinishdagi barcha haqiqiy tarmoqlarni topamiz. 4-qadam. 4-bo'lim usullaridan foydalanib va 3.1- teorema yordamida ularni aniqlashtirib f(0; x 2 ) = 0 va f(x 1 ; 0) = 0 tenglamalarining yechimlari sifatida x 1 = 0 va x 2 = 0 o'qlari bilan egri chiziqning kesishish nuqtalarini topamiz.. 5-qadam. P = (1; 0) va P = (0; 1) shartlar bilan qisqartirilgan tenglamalar yordamida x 1 = ∞ va x 2 = ∞ cheksizliklari bilan egri chiziqning kesishish nuqtalarini topamiz: Ularning har biri uchun biz (3.6). tipdagi yoyilmalar boshlang'ich hadlarini hisoblaymiz. 6-qadam.  N chegarasi qismini K 1 = {P : p 1 < 0; p 2 > 0} masdala konusi bilan x 1 → 0 , x 2 → ∞ da ,shunga o’xshsash x 1 → ∞ , x 2 → 0 da- K 1 = {P : p 1 > 0; p 2 < 0} masdala konusi bilan birga foydalanib egri chiziqning tarmoqlarini topamiz. 7-qadam. x 1 , x 2 → ∞ , da  N chegarasi qismini K 3 = {P : p 1 > 0; p 2 > 0} masdala konusi bilan birga foydalanib egri chiziqning tarmoqlarini topamiz. 8-qadam. X 0 maxsus nuqtalaridan tashqarida egri chiziq tarmoqlari kesishmasligini hisobga olib, egri egri chiziq tarmoqlari topilgan qismlarini tutashtiramiz. 3-misol (3.1 va 3.2-misollarning davomi). Bu erda (3.9) polinomga qadamlarimizni qo'llash quyidagilarni beradi. 1. Ko‘phad kopaytuvchilarga ajralmaydi. 2. U faqat bitta maxsus X 0 = 0 nuqtasiga ega. 3. Bu nuqta yaqinida ikkita (3.16) va (3.17). starmoqni topdik 41 4. Egri chiziq o'qlar bilan i faqat X = 0 nuqtada kesib o'tadi. 3. Egri chiziq x 1 ¿ ∞ va x 2 = ∞ cheksizliklar bilan kesishmaydi, chunki Q 1 va Q 2 uchlari ularga mos keladi.( 6. Q 2 va Q 1 uchlararning faqat U 2 0) va U 1 0) normal konuslari mos ravishda K 1 va K 2 masalalar konuslari bilan kesishadi (3-bo'limning 3.2-rasm). Shuning uchun, x 1 → 0 , x 2 → ∞ ,x1→ ∞ ,x2→ 0 da tarmoqlar yo’q 7. K 3 masala konusi cheksizlikda (3.19) tarmoqni bergan G3(1) qirrasiga mos keladi. 8. 3.1-rasmdagi egri chiziqning topilgan qismlarini tutashtirib, biz 2.2-rasmni olamiz., bunda puktir chiziq –bu (3.20). asimptota. 3.3. Ishlab chiqilgan algoritmlarning misollar yechishga tadbiqlari Faqat bitta maxsus nuqta X=0 ga ega bo’lgan quyidagi egri chiziqlarning eskizlarini chizing: 1- misol. Ushbu f = x 13 x 20 − x 12 x 20 + x 10 x 22 berilgan bo’lsin. Ko’phadning tashuvchilari uchta nuqtadan iborat. Q 1 = ( 3 ; 0 ) Q 2 = ( 2 ; 0 ) Q 3 = ( 0 ; 2 ) Ularning qavariq qobig’i bu uchlarga ega bo’lgan Nyuton uchburchagidir. q 2 Q 3 = ( 0 ; 2 ) 42 Г1(1) Г2(1) q1 Q 2 = ( 2 ; 0 ) Г3(1) Q 1 = ( 3 ; 0 ) 1.1-rasm Ko’phadning uchta qirrasi Γ 1( 1 ) , Γ2(1) , Γ 3( 1 ) bor. Γ 1( 1 ) = [ Q 1 ; Q 3 ] , Γ2(1)=[Q2;Q3] , Γ 3( 1 ) = [ Q 1 ; Q 2 ] Qisqartirilgan tenglama f 1 ( 1) = x 13 + x 22 = 0 x13+x22=0 x2=±√− x13 yechimga ega: Qisqartirilgan tenglama f 2 ( 1) = x 22 − x 12 = 0 x22− x12= 0 x2=±x1 yechimga ega: Qisqartirilgan tenglama f 3 ( 1) = x 13 − x 1 2 = 0 x 13 − x 12 = 0 x1= 0,x1=1 yechimga ega: Γ2(1) qirra holida x2= x1(1+y2) almashtirishdan so’ng f= x13− x12+x12(1+y2)2= x12((1+y2)2−1+x1) Qavslar ichidagi qisqartirilgan tenglama uchun ( 1 + y 2 ) 2 − 1 + x 1 = 0 y22+2y2+x1= 0 hosil bo’ladi. Ushbu ko’phadning tashuvchisi va ko’pburchagi 1.2- rasmda ko’rsatilgan. Q1=(0;2) Q 2 = ( 0 ; 1 ) Q3=(1;0) Ularning qavariq qobig’i bu uchlarga ega bo’lgan Nyuton uchburchagidir. 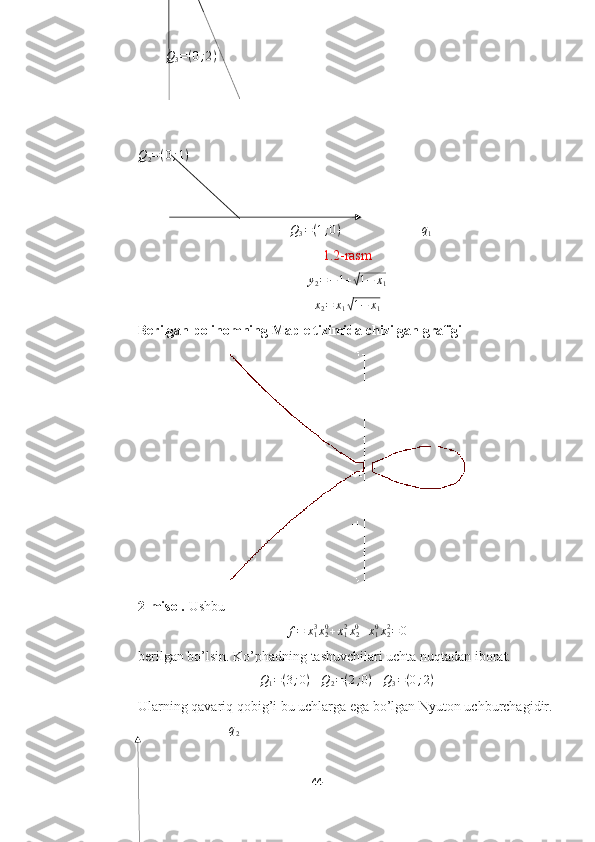q 2 43 Q3=(0;2) Q2=(0;1) Q3=(1;0) q 1 1.2-rasm y2=−1+√1− x1 x2= x1√1− x1 Berilgan polinomning Maple tizimida chizilgan grafigi 2 - misol. Ushbu f = x 13 x 20 + x 1 2 x 20 + x 10 x 22 = 0 berilgan bo’lsin. Ko’phadning tashuvchilari uchta nuqtadan iborat. Q 1 = ( 3 ; 0 ) Q 2 = ( 2 ; 0 ) Q 3 = ( 0 ; 2 ) Ularning qavariq qobig’i bu uchlarga ega bo’lgan Nyuton uchburchagidir. q 2 44 Q3=(0;2) Г1(1) Г2(1) q1 Q2=(2;0) Г3(1) Q1=(3;0) 2.1-rasm Ko’phadning uchta qirrasi Γ 1( 1 ) , Γ2(1) , Γ 3( 1 ) bor. Γ 1( 1 ) = [ Q 1 ; Q 3 ] , Γ2(1)=[Q2;Q3] , Γ 3( 1 ) = [ Q 1 ; Q 2 ] Qisqartirilgan tenglama f 1 ( 1) = x 13 + x 22 = 0 x 13 + x 22 = 0 x 2 = ± √ − x 13 yechimga ega: Qisqartirilgan tenglama f 2 ( 1) = x 22 + x 1 2 = 0 x 22 + x 1 2 = 0 x 2 = ± x 1 yechimga ega: Qisqartirilgan tenglama f 3 ( 1) = x 13 + x 12 = 0 x13+x12=0 x1= 0,x1=1 yechimga ega: Γ2(1) qirra holida x 2 = x 1 ( 1 + y 2 ) almashtirishdan so’ng f = x 13 + x 12 + x 12 ( 1 + y 2 ) 2 = x 12 (( 1 + y 2 ) 2 + 1 + x 1 ) = x 12 ( y 22 + 2 y 2 + x 1 + 2 ) Qavslar ichidagi qisqartirilgan tenglama uchun 45 (y 22 + 2 y 2 + x 1 + 2 ) = 0 hosil bo’ladi. Ushbu ko’phadning tashuvchisi va ko’pburchagi 2.2- rasmda ko’rsatilgan. Q1=(0;2) Q 2 = ( 0 ; 1 ) Q3=(1;0) Ularning qavariq qobig’i bu uchlarga ega bo’lgan Nyuton uchburchagidir. q2 Q3=(0;2) Q2=(0;1) Q3=(1;0) q 1 2.2-rasm y2=−1+√−1− x1 x2= x1√−1− x1 Berilgan polinomning Maple tizimida chizilgan grafigi 46 3 - misol. Ushbuf= x12x22+x13+x22 berilgan bo’lsin. Ko’phadning tashuvchilari uchta nuqtadan iborat. Q1=(2;2) Q2=(3;0) Q3=(0;2) Ularning qavariq qobig’i bu uchlarga ega bo’lgan Nyuton uchburchagidir. q2 Г1(1) Q1=(2;2) Q 3 = ( 0 ; 2 ) Г3(1) Г2(1) Q 2 = ( 3 ; 0 ) q 1 3.1-rasm Ko’phadning uchta qirrasi Γ 1( 1 ) , Γ2(1) , Γ 3( 1 ) bor. 47 Γ 1( 1 ) = [ Q 1 ; Q 3 ] , Γ2(1)=[Q2;Q3] , Γ 3( 1 ) = [ Q 1 ; Q 2 ] Qisqartirilgan tenglama f1(1)= x12x22+x22=0 x12x22+x22=0 x1= 0 yechimga ega: Qisqartirilgan tenglama f 2 ( 1) = x 22 + x 13 = 0 x 22 + x 1 3 = 0 \ x 2 = ± √ − x 13 yechimga ega: Qisqartirilgan tenglama f3(1)= x12x22+x13= 0 x 12 x 22 + x 13 = 0 x2=±√− x1 yechimga ega: Γ3(1) qirra holida x2=√− x1(1+y2) almashtirishdan so’ng f = x 12 x 1 2 ( 1 + y 2 ) 2 + x 13 + x 12 ( 1 + y 2 ) 2 = ( 1 + y 2 ) 2 = x 1 2 (( 1 + y 2 ) 2 + 1 + x 1 ) = x 12 ( x 1 2 y 22 + 2 x 1 2 y 2 + x 1 2 + y 22 + 2 y 2 + 1 + x 1 ) Qavslar ichidagi qisqartirilgan tenglama uchun (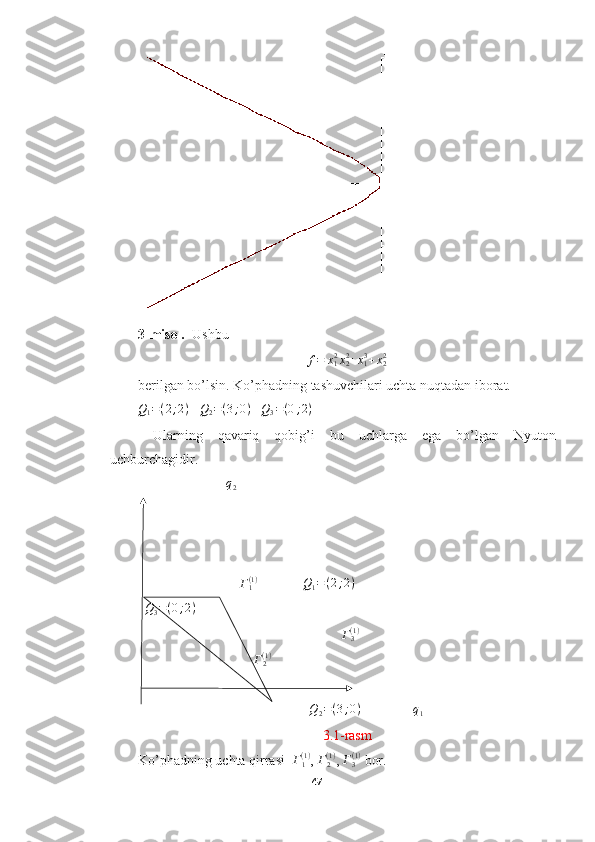x12y22+2x12y2+x12+y22+2y2+1+x1)=0 hosil bo’ladi. Ushbu ko’phadning tashuvchisi va ko’pburchagi 3.2- rasmda ko’rsatilgan. Q1=(2;2) , Q2=(2;1) , Q3=(2;0) , Q 4 = ( 0 ; 2 ) , Q 5 = ( 0 ; 1 ) , Q6=(1;0) . Berilgan polinomning Maple tizimida chizilgan grafigi 48 3.4. Darajali geometriya dasturiy ta'minoti haqida. Qavariq to'plamlar bilan ishlash uchun turli xil dasturlar mavjud. Bu erda biz faqat konveks qobiqlarni hisoblash uchun ham, ularning oddiy konuslarini hisoblash uchun ham ishlatilishi mumkin bo'lgan dasturlarni qisqacha tavsiflaymiz. O'z hisob- kitoblari uchun mualliflar hisoblash geometriyasining ko'plab muammolarini hal qilish uchun mo'ljallangan, bepul mavjud Qhull paketidan [9] foydalanganlar. Paketda yordamchi dasturlar (utilitalar) to'plami mavjud bo'lib, ular to'plamning qavariq qobiqini va qavariq ko'pburchakning boshqa parametrlarini hisoblaydigan qconvex dasturini o'z ichiga oladi. Ushbu mahsulot tijorat va bepul ko'plab dastur paketlarida qo'llaniladi. Masalan, Matlab , GNU Octave ilmiy hisoblash tizimlari , kompyuter algebra tizimlari Mathematica va Maple , SciPy va geometriya kutubxonalari mos ravishda Python va R dasturlash tillari uchun Qhull paketi bilan dasturiy interfeysga ega. Ushbu to'plamdan Maple kompyuter algebra tizimi bilan birgalikda algebraik birliklarni o'rganish uchun foydalanish mualliflarning ishida tasvirlangan [10]. Paketning asosiy xususiyati shundaki, hisob-kitoblar Hadamard ko'pburchak bilan ishlashda qulay bo'lgan ratsional sohada emas, balki haqiqiy sonlar yordamida amalga oshiriladi. Nyuton ko'pburchakni hisoblashda hisoblash natijalarini ratsional qiymatlarga etkazish uchun qo'shimcha qadamlar talab qilinadi. 49 2015 yil versiyasidan boshlab Maple kompyuter algebra tizimi PolyhedralSets paketini o'z ichiga oladi . Bu, xususan, to'plamning qavariq qobiqini hisoblash va uning H - yoki V - tasvirini berishga imkon beradi, ya'ni. chegara giper tekisliklari tenglamalari shaklida yoki chiziqli birikmasi chegaralanmagan qavariq qobiqni beradigan ekstremal nuqtalar va nurlar to'plami shaklida. Ushbu paketda barcha hisob- kitoblar ratsional sonlar sohasida amalga oshiriladi, bu Nyutonning ko'p yuzliligini o'rganish uchun undan foydalanishni biroz soddalashtiradi, lekin Hadamard ko'pyoqli bilan ishlashda uni foydasiz qiladi. PolyhedralSets to'plami Qhull to'plamiga nisbatan juda past ishlashga ega ekanligini unutmang . Quyida qavariq dekart ko‘pburchakning normal konuslarini hisoblash dasturining ro‘yxati keltirilgan (3.1-misol). with ( PolyhedralSets ) : SuppFolium := [[3 , 0] , [0 , 3] , [1 , 1 ] ] : ConvSuppFolium := ConvexHull ( PolyhedralSet ( SuppFolium ) ) : Relations ( ConvSuppFolium ) ; [ − x 1 − 2 x 2 ≤ − 3 , − x 1 − x 2 2 ≤ − 3 2 , x 2 + x 1 ≤ 3] Hisob-kitoblar natijasi qavariq qobiqning H - tasvirini beradi, undan oddiy vektorlarni (−1 , − 2) , (−1 , − 1/2) , (1 , 1) , topilgan holda olish oson. Hisoblash geometriyasi sohasidagi tadqiqotlar uchun kutubxonalarning katta tanlovi bepul tarqatilgan Sage kompyuter algebra tizimi tomonidan taqdim etilgan [11]. Bu sizga PPL (Parma polyhedral Library) [13], polymake , yuqorida qayd etilgan va boshqalar kabi kutubxonalar bilan ishlash imkonini beradi . Maple tizimida tekis algebraik egri chiziqlarni o'rganishga imkon beruvchi ajoyib algcurves to'plami mavjud: ularning eskizlarini yuqori aniqlik bilan yasash, ularning jinsini hisoblash, maxsus nuqtalarni topish, bir jinsli egri chiziqlar uchun [24] usuli yordamida ratsional parametrlashtirishni topish, elliptik egri chiziqlar uchun Weiershtrass normal shakliga keltirish va boshqalar. 50 XULOSA Ushbu bitiruv ishi algebraik chiziqlarni maxsus ko’pyoqliklar yordamida tadqiq qilishga bag’ishlangan. Bitiruv ishida har xil geometriyalar: Yevklid geometriyasi, affin geometriya, proyektiv geometriya va algebraik geometriyalar haqida ma’lumotlar keltirilib, ularning asosiy masalalari qarab chiqilgan va o’zaro taqqoslangan. Bu geometriyalarni o’z ichiga oluvchi darajali geometriya asoslari tekislikda o’rganilgan. Darajali geometriya yuqori darajali algebraik polinomlarni ularning daraja ko’rsatkichlaridan hosil qilingan tashuvchi va shu tashuvchi nuqtalarining geometrik o’rnidan iborat bo’lgan ko’pyoqlar yordamida tadqiqi qilishdan iborat. Ushbu malakaviy bitiruv ishida dekart yaprog’i kabi bir nechta tekis algebraik chiziqlar tadqiq qilingan. Bitiruv ishida ishlab chiqilgan algoritm asosida qaralayotgan algebraik chiziqlarning maxsus nuqtalari, shu nuqtalar 51 atrofida ularning yechimlarining asimptotik yaqinlashishlaridan iborat bo’lgan qatorlar tasvirlangan. Malakaviy bitiruv ishida qaralayotgan masalalarga kompyuter algebrasi tizimlarini qo’llash masalasi ham qarab chiqilgan. Foydalanilgan adabiyotlar 1. Брюно А. Д. Алгоритмы решения одного алгебраического уравнения// Программирование. 2019. № 1. С. 59—72. DOI: 10.1134/S0132347419 . 2. Клейн Ф. Лекции о развитии математики в XIX столетии: В 2-х томах. Т. 1 / под ред. М. М. Постников. М.: Наука, 1989. 456 с. 3. Ефимов Н. В. Высшая геометрия. 7-е изд. М.: ФИЗМАТЛИТ, 2004. 584 с. 4. Кострикин А. И., Манин Ю. И. Линейная алгебра и геометрия. 2-е изд. М.: Наука, 1986. 304 с. 5. Юнг Д. В. Проективная геометрия. М.: ИЛ, 1949. 186 с. 6. Шафаревич И. Р. Основы алгебраической геометрии. М.: МЦМНО, 2007. 590 с. 7. Брюно А. Д. Локальный метод нелинейного анализа дифференциальных уравнений. М.: Наука, 1979. 252 с. 8. Брюно А. Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М .: Наука , 1998. 288 с . 9. Barber C. B., Dobkin D. P., Huhdanpaa H. T. The Quickhull algorithm for convex hulls // ACM Trans. on Mathematical Software. 1996. Vol. 22, no. 4. P. 469–483. DOI: 10.1145/235815.235821. 52 10. Брюно А. Д., Батхин А. Б. Разрешение алгебраической сингулярности алгоритмами степенной геометрии // Программирование. 2012. № 2. С . 12— 30. 11. The Sage Developers. SageMath, the Sage Mathematics Software System (Version 9.1.1). 2020. DOI: 10.5281/zenodo.4066866. https://www.sagemath.org. 12. Fukuda K. cdd, cddplus and cddlib homepage. 2002. URL: http://www.cs. mcgill.ca/~fukuda/software/cdd_home/cdd.html. 13. Bagnara R., Hill P. M., Zaffanella E. The Parma Polyhedra Library: Toward a Complete Set of Numerical Abstractions for the Analysis and Verification of Hardware and Software Systems // Science of Computer Programming. 2008. Vol. 72, no. 1/2. P. 3–21. 14. Bruce King R. Beyond the quartic equation. Boston: Birkhäser, 1996. 149 p. 15. Умемура Х. Решение алгебраических уравнений с помощью тэта-констант // Лекции о тэта-функциях : Пер. с англ. / Д. Мамфорд. М.: Мир, 1988. С. 362— 370 . 16. Hadamard J. Etude sur les propriétés des fonctions entières et en particulier d’une fonction considérée par Riemann // Journal de mathématiques pures et appliquées 4 e série. 1893. T. 9. P. 171-216. 17. Курош А. Г. Курс высшей алгебры. М.: Наука, 1956. 431 с. 18. Калинина Е. А., Утешев А. Ю. Теория исключения: Учеб. пособие. СПб .: Изд - во НИИ химии СПбГУ , 2002. 72 с . 19. Gathen, J. von zur, Lücking T. Subresultants revisited // Theoretical Computer Science. 2003. Vol. 297, issue 1–3. P. 199–239. DOI: 10 . 1016 / S0304 - 3975(02)00639-4. 20. Батхин А. Б. Параметризация дискриминантного множества вещественного многочлена // Программирование. 2016. Т. 42, № 2. С. 8—21. 21. Акритас А. Г. Основы компьютерной алгебры с приложениями. М .: Мир , 1994. 544 с . 22. Puiseux V. Recherches sur les fonctions algébriques // Journal de mathématiques pures et appliquées 1 re série. 1850. T. 15. P. 365-480. 23. Гурса Э. Курс математического анализа. Т. 1. Ч. 2. М.-Л.: ГТТИ, 1933. 235 с . 24. Hoeij M. Rational parametrizations of algebraic curves using a canonical divisor // J. Symbolic Computation. 1997. Vol. 23. P. 209–227. 53

TEKIS ALGEBRAIK EGRI CHIZIQLARNI ULARNING KO’PYOQLIKLARI YORDAMIDA TADQIQ QILISH Mundarija KIRISH 3 I bob. Geometriyalar 1.1. Evklid va Affin geometriyasi 4 1.2. Proyektiv va Algebraik geometriya 6 1.3. Darajali geometriya 10 II bob. Darajali geometriya asoslari 2.1. Analitik funksiyalarning lokal masalalari 12 2.2. Funksiyalarning kichiklik tartibi 15 2.3. Tekis egri chiziqlarning kichiklik tartibi 16 2.4. Analitik funksiyalarning lokal xossalari 19 III bob . Tekis algebraik chiziqlarni ularning ko ’ pyoqliklari yordamida tadqiq qilish 3.1. Oddiy nuqtaning lokal tahlili. 34 3.2. Haqiqiy egri chiziqning eskizi. 41 3.3. Ishlab chiqilgan algoritmlarning misollar yechishga tadbiqlari 43 3.4. Darajali geometriya dasturiy ta'minoti haqida 49 XULOSA 52 FOYDALANILGAN ADABOYITLAR RO’YXATI 53 1

KIRISH Bitiruv malakaviy ishining dolzarbligi: Ushbu bitiruv malakaviy ishida keyingi yillarda keng o‘rganilayotgan sohalardan biri bo‘lgan darajali geometriya asoslari va uning tekis algebrik chiziqlarning xossalarini o’rganishga tadbiqlari o‘rganilgan. Jumladan, darajali geometriyaning asosiy tushunchalari, uning muhim elementlari hamda tadbiqlari o‘rganilgan. Bitiruv malakaviy ishining maqsadi: darajali geometriya metodlarini tekis algebrik chiziqlarning xossalarini o‘rganish uchun tadbiqlaridan iboratdir. Bitiruv malakaviy ishining vazifalari: Bitiruv malakaviy ishining vazifalari darajali geometriya metodlarini tekis algebrik chiziqlarning xossalarini o‘rganish uchun tadbiq etish, bu yo‘nalishga qizziqgan va o‘rganishni istagan talabalar, magistrlar va yosh olimlar uchun o‘zbek tilida muhim ma’lumotlar bazasini shakllantirishdan iborat. Bitiruv malakaviy ishining o ‘ rganilganlik darajasi: Ushbu malakaviy bitiruv ishida qo’yilgan talablar bajarildi, qo’yilgan vazifa yuzasidan ma’lumotlar o‘rganildi. Darajali geometriya, Nyuton ko’pyoqligi, qisqartma tenglamalar, algebraik chiziqlar va ularning eskizlarini yaratishda A.D. Bryuno, A.S.Soleev, A.B. Batxin, H.Nosirova, X. Ro’zimuradovlarning monongrafyalari [8], ilmiy maqolalaridan [1, 10, 20] foydalanildi. Bitiruv malakaviy ishining ob’yekti: Ushbu ishning ob’yekti tekis algebraik chiziqlar, ularning tashuvchilari, Nyuton ko’pyoqliklari, kompyuter algebrasi tizimlari hisoblanadi. Bitiruv malakaviy ishining predmeti: har xil geometriylar, darajali geometriya asoslari va usullaridan iborat. Bitiruv malakaviy ishida qo ‘ llanilgan metodikaning tavsifi: Ishda chiziqli va abstrakt algebraning usullaridan, geometrik usullar, matematik analiz usullari hamda daragali geometriya usullaridan foydalanilgan. 2

Bitiruv malakaviy ishi mundarija, kirish, uchta bob, xulosa va foydalanilgan adabiyotlar ro ‘ yxatidan iborat. Adabiyotlar ro ‘ yxati o’z ichiga keyingi yillarda nashr qilingan 23 ta adabiyotni olib, 54 betdan tashkil topgan. I bob. Geometriyalar 1.1. Evklid va Affin geometriyasi Geometriya turli jismlarning tuzilishini, figuralarni va ularning nisbiy holatini o'rganadi. Intuitiv ravishda hamma bu nima ekanligini tushunadi. Lekin birinchi marta geometriyaning ta'rifini F. Klein 1872 yilda Erlangen dasturida quyidagicha bergan: "Geometriya ikkita ob'ektning: fazo va uning almashtirishlari gruppasining kombinatsiyasidan iborat.” Agar har bir A koordinatalar almashtirishi bilan birga uning teskari almashtirishi A−1 mavjud bo’lsa, A∙A−1 almashtirishlar ko’paytmasi hech narsani o'zgartirmaydigan ayniy almashtirish bo'ladi. Turli fazolar va turli gruppalarning o’zaro ta’siri natijasida turli geometriyalar hosil bo’ladi. Quyida biz har biri avvalgisini o'z ichiga oladigan geometriyalarning ma'lum bir ketma-ketligini qarab chiqamiz. Bular Evklid, affin, proyektiv, algebraik va darajali geometriyalardan iborat. Barcha geometriylar bitta fazoda - haqiqiy n o'lchovli fazo R n quriladi, lekin har safar almashtirishlar gruppasi kengayadi. Evklid geometriyasi Bu yerda R n fazoda biz qo‘yidagi vektor uzunligini qaraymiz: ¿∨ X∨¿≝⟨X ,X ⟩ va X ∗ = AY ∗ almashtirishlar gruppasi ta’sirida bu uzunlik saqlanadi: ⟨ X,X ⟩ = ⟨ AY ∗ , AY ∗ ⟩ = ⟨ Y ,A ∗ AY ∗ ⟩ = ⟨ Y,Y ⟩ ya'ni A ∗ A = E — birlik matritsasi, E=( 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ 1) , 3

yokiA¿= A−1 . Bunday xususiyatga ega matritsalar ortogonal deyiladi. Ular R maydon ustida ortogonal xosmas kvadrat matritsalarning O ( n ) gruppasini hosil qiladi. Almashtirishlar gruppasi parallel ko’chirishni ham o'z ichiga oladi: X = X 0 + Y , (2.1) bu erda X 0 - tayinlangan vektor. Ushbu almashtirishlar ta’sirida burchaklar, yuzalar va hajmlar saqlanadi. Affin geometriyasi Bu erda ikkita fazo mavjud: asosiysi haqiqiy R n = { X = ( x 1 , x 2 , … , x n ) | x i ∈ R n , i = 1,2 , … , n } va unga qo’shma (ya'ni dual) bo’lgan R ¿ n = { Y = ( y 1 , y 2 , … , y n ) | y i ∈ R n , i = 1,2 , … , n } fazolar qaraladi. Bu yerda X ¿ = A X ' ∗ ¿ , Y ¿ = B Y ' ∗ ¿ ; det A , det B ≠ 0 ¿ ¿ almashtirishlar o’zaro qo’shma fazolarni vektorlarining skalyar ko’paytmalarini saqlaydi: ⟨ X , Y ⟩ = ¿ bu yerda X , X ' ∈ R n , Y , Y ' ∈ R ¿n dan iborat. Demak, A ∗ B = E, ya'ni B = ( A ∗ ) −1 . R n fazoning o’ziga o’zaro bir qiymatli affin akslantirishlari to'plami akslantirishlarini ko’pyatirish (ketma-ket bajarish)ga nisbatan gruppa tashkil qiladi va u Aff R n bilan belgilanganadi. Bu gruppa n-tartibli xosmas matrisalardan tashkil topgan to'la chiziqli gruppa GL(n,R) ga akslanadi, affin almashtirishlar gruppasiga (2.1) ko’rinishdagi parallel ko’chirishlar ham kiradi. Ushbu geometriyada to'g'ri chiziqlar, tekisliklar va har qanday chiziqli ko’pxilliklar mos ravishda to'g'ri chiziqlar, tekislik va chiziqli ko’pxilliklarga o’tadi. Bunday holda, 4

burchaklar saqlanib qolmaydi, lekin to'g'ri va dual fazolar vektorlari orasidagi ortogonallik saqlanib qoladi:⟨ X,Y ⟩ = 0=¿ ⟨X',Y'⟩ Ikki vektorning skalyar (yoki ichki) ko'paytmasidan tashqari n − 1 ta X1,... ,Xn−1∈Rn vektorlarining tashqi ko’paytmasi ham mavjud va u quyidagicha aniqlanadi. det ( I X 1 ⋮ X n − 1 ) = y1i1+… +ynin , bu yerda I=(i1,… ,in) va Y = ( y 1 , … , y n ) ∈ R n , X1,... ,Xn−1 . vektorlariga normal Y vektorni hisoblash imkonini beradi 1.2. Proyektiv va Algebraik geometriya Proyektiv geometriya. Quyidagi muammoni qarab chiqamiz: 2.1.-misol. Tekislikda L 1 va L2 parallel to’g’ri chiziqlar, ularga ortogonal M to’g’ri chiziq va kuzatish nuqtasi N berilgan bo’lsin. N nuqtadan M to’g’ri chiziqqa L1 va L2 to’g’ri chiziqlar qismlarini x → ∞ bo’lganda proyeksiya qilish talab qilinadi (2.1-rasm). 2.1-rasm. 5

O'xshashlar

MASHINALI O’QITISHDA GRADIENTLI TUSHISH ALGORITMINI CHIZIQLI REGRESSIYA YORDAMIDA TADQIQ QILISH
Yarimo'tkazgichlarning tarixini tadqiq qilish.
Matematik paketlar yordamida determinatlarning xossalarini tadqiq etish
YUQORI DARAJALI ALGEBRAIK TENGLAMALAR SISTEMALARINI GRYOBNER BAZISLARI YORDAMIDA YECHISH.
MARGANES IONLAR IMPLANTATSIYA QILINGAN KREMNIY MONOKRISTALLARI SIRT MORFOLOGIYASINI ATOM KUCH MIKROSKOPI YORDAMIDA TADQIQ QILISH