MASHINALI O’QITISHDA GRADIENTLI TUSHISH ALGORITMINI CHIZIQLI REGRESSIYA YORDAMIDA TADQIQ QILISH










![hosilalar deb ataladi. Berilgan p nuqtadagi n o‘lchamli f(x) funksiya uchun gradient
quyidagicha aniqlanadi:
∇ f( p ) =
[ ∂ f
∂ x
1 ( p )
:
∂ f
∂ x
n ( P ) ]
Teskari uchburchak nabla deb ataladigan belgidir va siz uni "del" deb o'qiysiz. Uni
qanday hisoblashni yaxshiroq tushunish uchun quyidagi ikki o'zgaruvchili funksiya
uchun qo'lda hisob-kitob qilaylik.
f(x)=0.5 x2+y2
Rasm 6.
f(x)=0.5 x2+y2 funksiyaning 3D grafigi
Faraz qilaylik, bizni p(10,10) nuqtadagi gradient qiziqtiradi:
∂ f ( x , y )
∂
x = x , ∂ f ( x , y )
∂
y = 2 y
shuning uchun
∇ f(x,y)=[
x
2y],∇ f(10,10 )=[
10
20 ]
11](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_11.png)









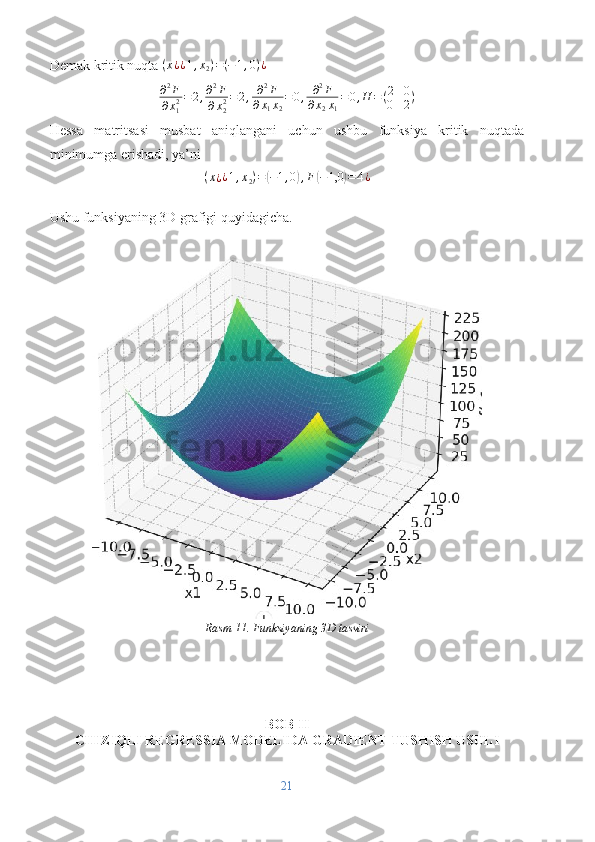


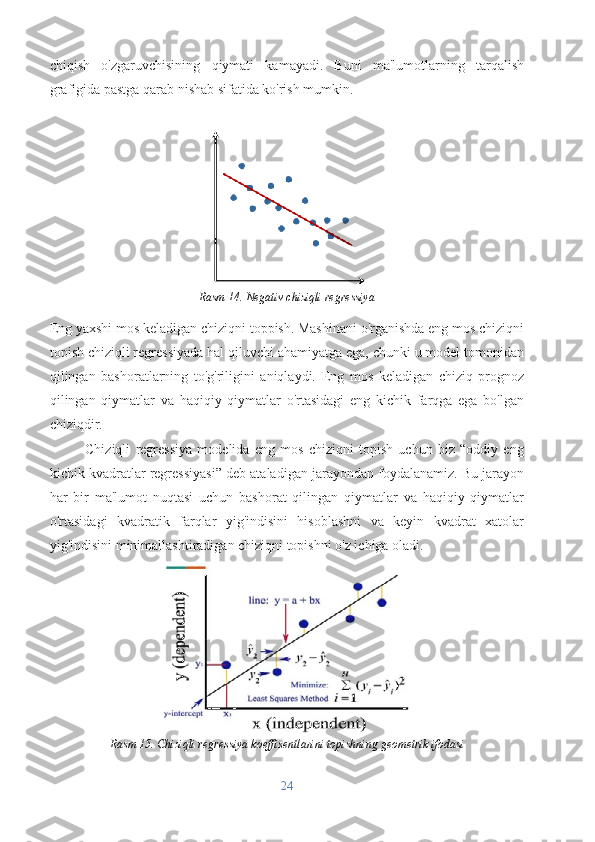




![umumlashtirilishini o'lchaydigan turli ko'rsatkichlar yordamida baholanishi
mumkin. Lineer regressiyada ishlatiladigan ba'zi umumiy ko'rsatkichlar:
Misol : Faraz qilaylik, bizda uyning kattaligiga qarab uy-joy narxini bashorat
qiluvchi chiziqli regressiya modeli mavjud. Bizda quyidagi haqiqiy narxlar (y) va
bashorat qilingan narxlar (y_hat) bo'lgan 10 ta ma'lumot nuqtasi mavjud:
y = [100, 150, 200, 250, 300, 350, 400, 450, 500, 550]
y_hat = [110, 140, 180, 240, 290, 320, 380, 420, 480, 520]
y_mean = yig'indi (y) / len (y) = 325
Kvadratlar regressiyasi yig'indisi (SSR): SSR prognoz qilingan qiymatlar va qaram
o'zgaruvchining o'rtacha qiymati o'rtasidagi kvadratik farqlar yig'indisini olish yo'li
bilan hisoblanadi. U mustaqil o'zgaruvchilar bilan izohlanadigan qaram
o'zgaruvchidagi o'zgaruvchanlikni ifodalaydi. Matematik jihatdan uni quyidagicha
ifodalash mumkin:
SSR = summa ((y_hat — y_mean)²) = 28300
Kvadratlar yig'indisi xatosi (SSE): SSE prognoz qilingan qiymatlar va qaram
o'zgaruvchining haqiqiy qiymatlari o'rtasidagi kvadratik farqlar yig'indisini olish
yo'li bilan hisoblanadi. Matematik jihatdan uni quyidagicha ifodalash mumkin:
SSE = summa((y — y_hat)²) = 26700
O'rtacha kvadrat xato (MSE): Bu ko'rsatkich bashorat qilingan va haqiqiy qiymatlar
o'rtasidagi o'rtacha kvadrat farqni o'lchaydi. U ma'lumotlar nuqtalari soniga
bo'lingan kvadrat qoldiqlar yig'indisi sifatida hisoblanadi. Pastroq MSE yaxshi
ishlashni ko'rsatadi. Matematik jihatdan uni quyidagicha ifodalash mumkin:
MSE = (1/n) * summa((y — y_hat)²) = 2670
Root Mean Squared Error (RMSE): Bu ko'rsatkich MSE ning kvadrat ildizini
o'lchaydi va bog'liq o'zgaruvchi bilan bir xil birliklardagi xatolarni izohlash uchun
foydalidir. Matematik jihatdan uni quyidagicha ifodalash mumkin:
RMSE = sqrt(MSE) = sqrt(2670) = 51,68
O'rtacha mutlaq xato (MAE): Bu ko'rsatkich bashorat qilingan va haqiqiy qiymatlar
o'rtasidagi o'rtacha mutlaq farqni o'lchaydi. U MSE ga qaraganda chetga
29](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_29.png)






![Ilovalar
import tkinter as tk
from tkinter import scrolledtext
from time import sleep, time
import threading
import sympy as sp
from math import sqrt
from copy import deepcopy
class NotSolvedException(Exception):
pass
class WrongParametr(Exception):
pass
class StopLoopException(Exception):
pass
def get_gradient(func: str) -> tuple[list[str], int]:
""" Funksiya gradientini aniqlaydigan funksiya.
Bunda o'zgaruvchilar x1,x2,x3,x4,x5 ... x100 ko'rinishida bo'lishi shart
(ya'ni a,b,c va hokazolar qabul qilinmaydi).
Ushbu funksiya grafikda faqat qozon shaklini hosil qilgandagina ishlaydi.
"""
def _(s: str) -> str:
return s.replace(' ', '').replace('\n', '').replace('\t', '')
vars = []
38](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_38.png)
![var_count = 0
for i in range(1, 101):
if f'x{i}' in func:
vars.append(f'x{i}')
var_count = 0 + i
vars = ','.join([f'x{i}' for i in range(1, var_count + 1)])
if var_count == 1:
var_list = [sp.symbols(vars)]
else:
var_list = list(sp.symbols(vars))
new_func = func + ""
for i in range(var_list.__len__()):
new_func = new_func.replace(f'x{var_list.__len__() - i}', '1')
try:
eval(new_func)
except Exception:
raise WrongParametr("Funksiyada ortiqcha belgilar mavjud.\nFaqat quyidagi
o'zgaruvchilarni ishlating: x1,x2,x3,x4 ...")
gradient = [str(sp.diff(func, var)) for var in var_list]
is_access = False
for i in range(var_count):
grad_two = str(sp.diff(gradient[i], var_list[i]))
if _(grad_two) != '0':
is_access = is_access or True
grad_three = str(sp.diff(grad_two, var_list[i]))
if _(grad_three) != '0':
raise WrongParametr("Funksiya talabga javob bermaydi")
if not is_access:
raise WrongParametr("Funksiya talabga javob bermaydi")
return gradient, var_count
def norm(vc: list[float]):
""" vektorning normasini hisoblaydi """
return sqrt(sum(list(map(lambda x: x*x, vc))))
def solve_with_gradient(gradient: list[str], values: list[float]):
""" gradient va vektorni birgalikda hisoblaydi """
def _(func: str, _values: list[float]):
for i in range(len(_values)):
func = func.replace(f'x{i+1}', str(_values[i]))
try:
return eval(func)
except:
raise NotSolvedException
if len(gradient) != len(values):
raise WrongParametr("Gradient va qiymatlar vektori o'lchovi mos emas")
return list(map(lambda x: _(x, values), gradient))
def subtract_two_vc(vc1: list[float], vc2: list[float]):
39](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_39.png)
![if len(vc1) != len(vc2):
raise WrongParametr("vc1 va vc2 o'lchamlari mos emas")
return list(map(lambda i: vc1[i]-vc2[i], range(vc2.__len__())))
def multiple_vc_and_num(vc: list[float], num: float):
return list(map(lambda x: x*num, vc))
def f_solve(func: str, values: list[float]):
for i in range(len(values)):
func = func.replace(f'x{i+1}', str(values[i]))
return eval(func)
class GetCoordinateZero:
def __init__(self) -> None:
self.stop_flag = False
def get_coordinate_zero(self, func: str, *, eps: float = None,
x0: list[float] = None, t: float = None):
""" Matematik funksiyaning boshlang'ich qiymatini aniqlaydigan funksiya """
eps = eps or 0.01
t = t or 0.5
gradient, var_count = get_gradient(func)
x0 = x0 or [1] * var_count
xk: list[float] = deepcopy(x0)
if t == 1.0:
raise WrongParametr("t`ning qiymati 1.0 bo'lishi mumkin emas")
counter = 0
last_grad_norm = 0
last_grad_norm_counter = 0
while True:
counter += 1
if self.stop_flag:
raise StopLoopException
grad_vc_solve = solve_with_gradient(gradient, xk)
norm_dvs = norm(grad_vc_solve)
if norm_dvs < eps:
return xk, counter
xk_p_1: list[float] = subtract_two_vc(xk, multiple_vc_and_num(grad_vc_solve, t))
xk = deepcopy(xk_p_1)
if last_grad_norm <= norm_dvs:
last_grad_norm_counter += 1
if last_grad_norm_counter == 20:
raise NotSolvedException
last_grad_norm = deepcopy(norm_dvs)
class GUI:
def __init__(self) -> None:
self.window = tk.Tk(className="Gradient tushish")
self.window.geometry('800x500+100+100')
40](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_40.png)

![self._eps_label = tk.Label(self.window, text="Aniqlik koeffitsentini kiriting",font=('Arial
10'))
self._eps_label.place(x=410, y=105)
self._solve_label = scrolledtext.ScrolledText(self.window, wrap=tk.WORD, font=('Arial 12'),
bd=0, highlightthickness=0)
self._solve_label.place(x=10, y=180, width=780, height=200)
self._solve_label.config(state=tk.DISABLED)
def set_text(self, txt: str):
self._solve_label.config(state=tk.NORMAL)
self._solve_label.delete('1.0', tk.END)
self._solve_label.insert(tk.INSERT, txt)
self._solve_label.config(state=tk.DISABLED)
def force_thread_func(self):
func = self._func_input.get()
t = self._t_input.get()
eps = self._eps_input.get()
func = func.replace('^', '**')
if func.replace(' ', '').__len__() == 0:
self.set_text("Funksiyani kiriting !")
return
try:
t = float(t)
except:
self.set_text(f"t`ning qiymati haqiqiy son bo'lishi kerak !")
return
try:
eps = float(eps)
except:
self.set_text("Aniqlik koeffitsenti haqiqiy son bo'lishi kerak!")
return
try:
start = time()
points, counter = self.solve_obj.get_coordinate_zero(func, t=t,eps=eps)
finish = time()
except NotSolvedException:
self.set_text("Yechimni aniqlab bo'lmadi. \nIltimos parametrlarni qayta ko'rib chiqing.")
return
except WrongParametr as wp:
self.set_text(str(wp.args[0]))
return
except StopLoopException:
self.set_text("To'xtatildi")
return
except Exception as ex:
self.set_text(f'Nomalum xatolik yuz berdi: {ex}')
return
txt = ""
f_zero = "" + func
42](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_42.png)
![for i in range(len(points)):
txt += f'x{i+1} = {points[i]:.12f}\n'
f_zero = f_zero.replace(f'x{len(points) - i}', f'({points[len(points) - i - 1]})')
txt += f'F = {eval(f_zero):.12f}\n'
txt += f"\n\nIteratsiyalar soni: {counter}\nHisoblash vaqti: {(finish-start):.5f} sekund."
self.set_text(txt)
if __name__ == '__main__':
GUI()
import tkinter as tk
import os
from tkinter import filedialog, messagebox
import pandas as pd
from math import fabs
from sklearn import linear_model
import warnings
"""
Ushbu kod ishlashi uchun bir nechta paketlar kerak bo'ladi.
Ularni yuklab olish uchun terminalga ushbu kodlarni yozasiz
Windows uchun:
pip install pandas
pip install scikit-learn
Ubuntu yoki Linux uchun:
sudo apt install python3-tk
pip install pandas
pip install scikit-learn
"""
def get_solve_in_csv(csv_file_path: str, result_key: str, target_values: list[float]):
""" .csv fayldan ma'lumotni o'qib oladi va ushbu modelga yarasha model tayyorlaydi.
* csv_file_path: str - bu fayl manzili
* result_key: str - bu fayldagi asosiy kelib chiqishi kerak bo'lgan qiymat
* target_values: list[str] - bu bashorat qilinishi kerak bo'lgan ma'lumot
43](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_43.png)
![Qaytish: dict[Any]
* koeffitsentlar
* korrelyatsiya koefftisenti
* bashorat qiymati
"""
data = pd.read_csv(csv_file_path)
data = data.fillna(0)
X = data.drop(result_key, axis=1)
y = data[result_key]
model = linear_model.LinearRegression()
model.fit(X, y)
r_squared = model.score(X, y)
returned_dict = {}
returned_dict['coef'] = model.coef_
returned_dict['free'] = model.intercept_
returned_dict['r'] = r_squared
returned_dict['target_result'] = model.predict([target_values])[0]
return returned_dict
class CustomInput:
def __init__(self,window: tk.Tk, width: int, height: int, position_x: int, position_y: int, *args,
**kwargs):
self.input = tk.Entry(window, font=('Arial 10'), *args, **kwargs)
self.input.place(height=height, width=width, x=position_x, y=position_y)
def get_text(self):
return self.input.get()
def set_text(self, text: str):
self.input.delete(0, tk.END)
self.input.insert(0, text)
def delete(self):
self.input.destroy()
class CustomButton:
def __init__(self, window: tk.Tk, text: str, width: int, height: int, position_x: int, position_y: int,
*args, **kwargs):
self.button = tk.Button(window, text=text, *args, **kwargs)
self.button.place(height=height, width=width, x=position_x, y=position_y)
def delete(self):
self.button.destroy()
class GUI:
def __init__(self, *args, **_) -> None:
self.filename: str = None
self.data: pd.DataFrame = None
self.columns: list[str] = None
self.value_inside = None
44](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_44.png)
![self.window = tk.Tk(className=_['window_name'])
self.window.geometry(f'{_["screen_width"]}x{_["screen_height"]}')
self.window.configure(bg='#e6e6ff')
self.keys_info: list[tk.Widget] = []
self.value_inputs: list[CustomInput] = []
self.coeffitsents: list[tk.Label] = []
self.buttons_draw()
self.labels_draw()
self.inputs_draw()
self.others_draw()
self.window.mainloop()
def buttons_draw(self):
""" Barcha boshlang'ich buttonlar shu yerda chiziladi """
self.button_open_file_dialog = CustomButton(self.window, text='CSV faylni tanlang',
font=('Arial 10'), width=440, height=30, position_x=10, position_y=0, command=self.select_file)
self.button_solve = CustomButton(self.window, text='Hisoblash', font=('Arial 10'),
width=440, height=30, position_x=550, position_y=260, command=self.solve_action)
self.button_clear = CustomButton(self.window, text='Tozalash', font=('Arial 10'), width=440,
height=30, position_x=550, position_y=290, command=self.clear_action)
def clear_action(self):
""" Tozalash tugmasi bosilganda shu funksiya ishlaydi """
if self.filename:
self.draw_target_inputs(self.value_inside.get())
for i in self.value_inputs:
i.set_text('')
self.r_input.set_text('0.5')
self.show_target_res.config(text="Umumiy natija: Mavjud emas")
def solve_action(self):
""" Hisoblash tugmasi bosilganda shu funksiya ishlaydi """
if not self.filename:
self.error_view("Fayl tanlanmagan", "Iltimos avval kerakli faylni tanlang !")
return
absolute_error = self.r_input.get_text()
if not absolute_error:
self.error_view("Ma'lumot to'liq emas", "Iltimos korrelyatsiya koeffitsientini kiriting")
return
try:
absolute_error = float(absolute_error)
except:
self.error_view("String konvertatsiya xatoligi", "Korrelyatsiya koeffitsienti son bo'lishi
kerak")
return
if fabs(absolute_error) > 1.0:
self.error_view("Noto'g'ri qiymat", "Korrelyatsiya koeffitsienti moduli 1 dan kichik
bo'lishi shart")
45](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_45.png)
![return
target_values: list[float] = []
for i in range(len(self.value_inputs)):
text = self.value_inputs[i].get_text()
if not text:
self.error_view("Ma'lumotlar to'liq emas", f"Iltimos `{self.keys_info[i]['text']}`ning
qiymatini kiriting")
return
try:
target_values.append(float(text))
except:
self.error_view("String konvertatsiya xatoligi", f"`{self.keys_info[i]['text']}` maydoniga
son kiriting!")
return
res = get_solve_in_csv(self.filename, self.value_inside.get(), target_values)
if res['r'] < absolute_error:
self.error_view("Natijalar yaxshi emas!", "Modeldagi korrelyatsiya koeffitsenti talabga
javob bermaydi")
return
self.show_target_res.config(text="Umumiy natija: " + str(res['target_result']))
def inputs_draw(self):
""" Boshlang'ich inputlar shu yerda chiziladi """
self.r_input = CustomInput(self.window, 440, 30, 10, 290)
self.r_input.set_text(0.5)
def labels_draw(self):
""" Boshlang'ich labellar shu yerda chiziladi """
self.file_name_info = tk.Label(self.window, text='Fayl: Tanlanmagan', font=('Arial 10'),
relief=tk.FLAT)
self.file_name_info.place(x=10, y=40, width=440, height=30)
self.file_cols_info = tk.Label(self.window, text='Ustunlar: Tanlanmagan', font=('Arial 10'),
relief=tk.FLAT)
self.file_cols_info.place(x=10, y=70, width=440, height=30)
self.file_rows_info = tk.Label(self.window, text='Ma\'lumotlar hajmi: Tanlanmagan',
font=('Arial 10'), relief=tk.FLAT)
self.file_rows_info.place(x=10, y=100, width=440, height=30)
self.key_select_info = tk.Label(self.window, text='Asosiy qiymat kalitini tanlang',
font=('Arial 10'), relief=tk.FLAT)
self.key_select_info.place(y=0, x=550, width=440, height=30)
tk.Label(self.window, text='Nomlar:', font=('Arial 10'), relief=tk.RIDGE).place(y=150, x=10,
width=80, height=30)
tk.Label(self.window, text='Qiymatlar:', font=('Arial 10'), relief=tk.RIDGE).place(y=180,
x=10, width=80, height=30)
tk.Label(self.window, text='Koeffitsentlar:', font=('Arial 9'), relief=tk.RIDGE).place(y=210,
x=10, width=80, height=30)
46](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_46.png)
![tk.Label(self.window, text='Minimal korrelyatsiya koeffitsientini kiriting', font=('Arial 10'),
relief=tk.FLAT).place(y=260, x=10, width=440, height=30)
self.show_r = tk.Label(self.window, text="Korrelyatsiya koeffitsienti: Fayl tanlanmagan",
relief=tk.FLAT, font=('Arial 10'))
self.show_r.place(y=330, x=10, width=440, height=30)
self.show_target_res = tk.Label(self.window, text="Umumiy natija: Mavjud emas",
relief=tk.FLAT, font=('Arial 10'))
self.show_target_res.place(y=360, x=10, width=440, height=30)
self.show_free_coef = tk.Label(self.window, text="Ozod koeffitsent: Fayl tanlanmagan",
relief=tk.FLAT, font=('Arial 10'))
self.show_free_coef.place(y=390, x=10, width=440, height=30)
def others_draw(self):
""" OptionMenu shu yerda chiziladi """
self.value_inside = tk.StringVar(self.window)
self.value_inside.set("Fayl tanlanmagan")
self.select_main_key = tk.OptionMenu(self.window, self.value_inside, value='')
self.select_main_key.place(y=40, x=550, width=440, height=30)
self.select_main_key.config(state=tk.DISABLED, relief=tk.GROOVE)
def select_file(self):
""" Open File Dialog ochilishida ishlaydihgan funksiya """
filename = filedialog.askopenfilename(initialdir=os.getcwd(), title="CSV faylni tanlang",
filetypes=(('CSV fayllar', '*csv'),))
if not (not filename or filename == ()):
self.filename = filename
data = pd.read_csv(self.filename)
self.columns = data.columns
self.file_name_info.config(text='Fayl: ' + self.filename.split('/')[-1])
self.file_cols_info.config(text='Ustunlar: ' + ','.join(self.columns))
self.file_rows_info.config(text='Ma\'lumotlar hajmi: ' + str(len(data)))
self.select_main_key.destroy()
self.value_inside = tk.StringVar(self.window)
self.value_inside.set(self.columns[-1])
self.select_main_key = tk.OptionMenu(self.window, self.value_inside, *self.columns,
command=self.select_func)
self.select_main_key.place(y=40, x=550, width=440, height=30)
self.select_main_key.config(relief=tk.GROOVE)
self.show_target_res.config(text="Umumiy natija: Mavjud emas")
self.draw_target_inputs(self.value_inside.get())
def select_func(self, *args, **kwarg):
47](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_47.png)
![""" OptionMenu qayta tanlangan vaqtda shu funksiya ishlaydi """
self.draw_target_inputs(self.value_inside.get())
def draw_target_inputs(self, ignore: str):
""" Yangilanish vaqtida inputlarni qayta chizadigan funksiya """
for i in range(len(self.keys_info)):
self.keys_info[i].destroy()
self.value_inputs[i].delete()
self.coeffitsents[i].destroy()
self.value_inputs.clear()
self.keys_info.clear()
self.coeffitsents.clear()
res = get_solve_in_csv(self.filename, self.value_inside.get(), list(map(float,
'0'*(len(self.columns)-1))))
counter = 0
for i in range(len(self.columns)):
if self.columns[i] == ignore:
continue
label = tk.Label(self.window, text=self.columns[i], font=('Arial 10'), relief=tk.RIDGE)
label.place(x=90 + counter*80, y=150, width=80, height=30)
self.keys_info.append(label)
self.value_inputs.append(CustomInput(self.window, 80, 30, 90+counter*80, 180))
label = tk.Label(self.window, text=f"{res['coef'][counter]:.7f}", relief=tk.FLAT,
font=('Arial 10'))
label.place(x=90 + counter*80, y=210, width=80, height=30)
self.coeffitsents.append(label)
counter += 1
self.show_r.config(text="Korrelyatsiya koeffitsienti: " + str(res['r']))
self.show_free_coef.config(text="Ozod koeffitsient: " + str(res['free']))
def error_view(self, error_screen: str, error_text: str):
""" Xatolik xabarini ekranga chiqaradi """
messagebox.showerror(error_screen, error_text)
if __name__ == '__main__':
warnings.filterwarnings('ignore')
GUI(
window_name = "Liner prediction problem solver",
screen_width = 1000,
screen_height = 450
)
48](/data/documents/8a5341d8-6e43-49d2-8ec5-ecc4300cb799/page_48.png)
MAVZU: MASHINALI O’QITISHDA GRADIENTLI TUSHISH ALGORITMINI CHIZIQLI REGRESSIYA YORDAMIDA TADQIQ QILISH MUNDARIJA KIRISH 3 BOB I GRADIENT TUSHISH USULIGA MATEMATIK NAZAR 1.1 Gradient tushish usuli: asosiy tushunchalar 7 1.2 Gradient tushish usuli algoritmi, misollar 13 1.3 Gradient tushish usuli uchun dasturiy vosita 19 BOB II CHIZIQLI REGRESSIA MODELIDA GRADIENT TUSHISH USULI 2.1 Mashinali o’qitishda chiziqli regressia 23 2.1.1 Bir o’zgaruvchili chiziqli regressia 24 2.1.2 Ko’p o’zgaruvchili chiziqli regressia 27 2.2 Gradient tushish usulining chiziqli regressiada qo’llanilishi: maqsad funksiya 28 2.3 Chiziqli regressia modeli yordamida uy-joy narxlarini o’rganish 31 2.3.1 Ma’lumot yig’ish va qayta ishlash 32 2.3.2 Ma’lumotlarni o’qitish, model parametrlarini aniqlash 34 2.4 Chiziqli regressiya modeli uchundasturiy vosita 36 Adabiyotlar ro’yxati 38 Ilovalar 39 1
Kirish Masalaning qo‘yilishi. Gradient tushush usuli va uning mashinali o’qitish algoritmlaridan biri bo’lgan chiziqli regressiyada qo’llanilishini o’rganish, bu algoritmlarni amaliy qo’llash uchun uy-joy narxlarini regression tahlil qilish hamda ushbu usul va algoritmlarga asoslangan dasturiy vositalar ishlab chiqish. Mavzuning dolzarbligi. Bugunguni kunda juda ko’plab sohalar (tavsiya tizimlari, tasvirlarni aniqlash, tabiiy tilni qayta ishlash va moliyaviy bashoratlar) dagi turli xil hayotiy masalalarni yechishda ularga oid tarixiy ma’lumotlar, mashinali o’qitish algoritmlari, jumladan chiziqli regressia algoritmi orqali tahlil qilinib, eng yaxshi yechim, tavsiya, bashorat yoki qarorlar qabul qilinmoqda. Chiziqli regressiya algoritmi bu nazoratli o’qitish algoritmi bo’lib, u kirish xususiyatlari va maqsadli o'zgaruvchi o'rtasidagi chiziqli munosabatni aniqlashdan iborat. Chiziqli resgressiya natijalarining aniqligi, chiziqli munosabat koeffisentlarining aniqligiga bo’gliq bo’lib, u odatda gradient tushish usullari orqali aniqlanadi. Shu nuqtai nazardan chiziqli regressiya modelini qurishda gradient tushish usulini tadqiq qilish va bu usulga asoslangan dasturiy vosita ishlab chiqish muhim hisoblanadi. Ishning maqsad va vazifalari. Bitiruv malakaviy ishning asosiy maqsad va vazifasi bu chiziqli regressiya modelini qurish jarayonida gradient tushish usumining o’rnini anglash va bu usulga asoslangan dasturiy vosita ishlab chiqishdan iborat. Ilmiy-tatqiqot usullari. Ushbu bitiruv malakaviy ishida, chiziqli regressiya modelini qurishda gradient tushish usulining qo’llanilishini tadqiq qilish uchun matematik analiz, ehtimollar nazaryasi va matematik statistika, mashinaviy o’qitish hamda python dasturlash tili kurslarining ba’zi tushuncha, usul va yondoshuvlaridan foydalanilgan. Mavzuning o‘rganilish darajasi. 2
Chiziqli regressiya 19-asr oxiri va 20-asr boshlarida Frensis Galton va Karl Pirson ishlariga borib taqaladigan boy tarixga ega. Uning uzoq vaqtdan beri qo'llanilishi va rivojlanishi uni to'liq tushunishga yordam berdi. Chiziqli regressiya modellari mashinali o'qitish va statistikada eng yaxshi o'rganilgan va fundamental usullardan biridir. Ularning keng qamrovli o'rganilishi va qo'llanilishi bir necha omillarga bog'liq: Oddiylik va tushunarlilik: Chiziqli regressiya modellarini tushunish va izohlash oson. Bog'liq va mustaqil o'zgaruvchilar o'rtasidagi bog'liqlik aniq bo'lib, model bashoratlarini tushuntirishni osonlashtiradi. Nazariy asos: Chiziqli regressiya mustahkam nazariy asosga ega. Eng kichik kvadratlarni baholash tamoyillari, chiziqli modelning taxminlari va baholovchilarning xususiyatlari yaxshi tasdiqlangan. Ushbu nazariy asoslash modelning xatti-harakati va cheklovlarini tushunishga yordam beradi. Keng qo'llanilishi: Chiziqli regressiya iqtisodiyot, biologiya, muhandislik va ijtimoiy fanlar kabi turli sohalarda qo'llanilishi mumkin. Uning ko'p qirraliligi uni turli sohalarda qimmatli vositaga aylantiradi. Kengaytmalar va variantlar: Chiziqli regressiya muayyan ehtiyojlarni qondiradigan ko'plab kengaytmalar va variantlarga ega: Bir va ko’p o’zgaruvchili chiziqli regressiya: oddiy chiziqli regressiyani bir nechta bashorat qiluvchilarga kengaytiradi. Ko’pxadli regressiya: Polinom atamalarini kiritish orqali chiziqli bo'lmagan munosabatlarni modellashtiradi. Ridge va Lasso regressiyasi: haddan tashqari moslashishning oldini olish uchun tartibga solishni joriy qiling. Dasturiy ta'minot va asboblarni qo'llab-quvvatlash: 3
Chiziqli regressiya R, Python (scikit-learn, statsmodels), MATLAB va SAS kabi ko'plab dasturiy vositalar va kutubxonalar tomonidan qo'llab-quvvatlanadi. Ushbu vositalar foydalanish uchun qulay dasturlarni taqdim etadi va model yaratish, baholash va diagnostika qilishni osonlashtiradi. Ta'lim maqsadlarida foydalanish: Chiziqli regressiya ko'pincha statistika va mashinali o'qitish kurslarida o'qitiladigan birinchi modellardan biridir. Uning soddaligi uni yanada murakkab modellar va texnikalarni o'rganish uchun ajoyib boshlanish nuqtasiga aylantiradi. Tadqiqotning ilmiy yangiligi. Bitiruv malakaviy ishida olingan natijalar amaliy-uslubiy xarakterga ega bo‘lib, ishda ko’p o’zgaruvchili qavariq funksiyalarning ekstremumlari (maksimum yoki minimum) ni topish uchun gradient tushish usuliga asoslangan dasturiy ta’minot yaratligan. Bu dasturiy ta’minot Python dasturlash tilida yaratilgan bo’lib u vizuallashgan qulay interfeysga ega. Tadqiqot predmeti va ob’ekti. Tadqiqotning predmeti “Mashinaviy o’qitish”, “Mashinaviy o’qitishda optimallashtirish usullari”, “Kompyuter ilmlarida statistik modellar”, “Ehtimollar nazaryasi va matematik statistika” , “Matematik analiz”, “Python dasturlash tili” va shu kabi fan sohalari bo‘lib, ob’ekti chiziqli regressiya modeli va gradient tushish usulidan iborat. Tatqiqotnig ilmiy va amaliy ahamiyati. Ishda olingan natijalar va unda qo‘llanilgan usullardan turli iqtisodiy, ijtimoiy sohalarning ko‘pgina amaliy masalalarini tadqiq qilishda, “Ehtimollar nazaryasi va matematik statistika”, “Matematik analiz”, “Kompyuter ilmlarida statistik modellar” va shu kabi fanlarning amaliy mashg‘ulotlari o‘quv jarayonlarida dasturiy vosita sifatida foydalanish mumkin. Ishning tuzilishi. Ushbu ish kirish, ikki bob, xulosa, foydalanilgan adabiyotlar ro‘yxati va ilovalardan iborat. I bob uchta paragrafdan iborat bo‘lib, uning birinchi va ikkinchi paragrafida adabyotlardan foydalanilgan holda, gradient tushish usuli haqida umumiy tushunchalar, usul algoritmi keltirilgan va bu usul yordamida misollar yechilgan. 4
Uchinchi paragrafda gradient tushish usuliga asoslanib ishlab chiqilgan dasturiy vosita haqida ma’lumotlar keltirilgan. II bob uchta paragrafdan iborat bo’lib birinchi paragraph ikkita qism paragrafdan iborat bo’lib, mos ravishda, bir o’zgaruvchili va ko’p o’zgaruvchili chiziqli regressiyalar haqida ma’lumotlar keltirilgan. Ikkinchi paragraf gradient tushish usilining chiziqli regressia modelida qo’llanilishiga bag’ishlangan bo’lib, maqsad funksiyani tanlash va uning parametrlarini aniqlashga e’tibor qaratilgan. Bu bobning uchinchi paragrafida mavzuda doir amaliy masala qaralgan, ya’ni chiziqli regressiya algoritmiga asoslanib uy-joy narxlarini bashorat qilish modelini ishlab chiqishga qaratilgan bo’lib u ikkita ta qism paragrafdan iborat. Birinchi qism paragrafda uy-joy narxlariga tegishli ma’lumotlarni to’lash va qayta ishlash qaralgan, ikkinchi qism paragrafda model parametrlarini aniqlash va model natijasining aniqligini baholashga qaratilgan. Olingan natijalarning qisqacha mazmuni. Bitiruv malakaviy ishida chiziqli regressiya modelini qurish jarayonida, gradient tushish usulining o’rni, qo’llanilishi o’rganildi va gradient tushish usuliga asoslangan dasturiy vosita ishlab chiqilgan. Chiziqli regrsssiya modelida gradient tshish usulini yanada yaxshiroq anglsh uchun amaliy masala yechilgan ya’ni uy-joy narxlari chiziqli regressiya algoritmi yordamida tahlil qililinib bashorat qilivchi model ishlab chiqilgan. 5
