logo
  1. Bosh sahifa
  2. Referatlar
  3. Umumiy
  4. Noravshan to’plamlarning asosiy tushunchalari va tariflari

Noravshan to’plamlarning asosiy tushunchalari va tariflari

Yuklangan vaqt:

08.08.2023

Ko'chirishlar soni:

0

Hajmi:

746.09375 KB
Ko'chirib olish
Mav zu:Norav shan t o’plamlarning asosiy t ushunchalari v a t arifl ari Reja: Kirish 1. Norav shan t o’plamlar nazariy asi 2. Asosiy at ama v a t ushunchalar 3. Norav shan t o’plam t ushunchasi Foy dalanilgan adabiy ot lar KIRISH Hozirgi vaqtda haqiqiy jarayonlarni mod е llashtirish va muqobillashtirishda noaniqliklarni hisobga olish zaruriyati h е ch kimda shubha tug’dirmay qo’ydi. Ayni vaqtda noaniqlikni qo’llashga doir klassik nazariy-ehtimollik yondashuvning ch е klanishlarini anglash oxirgi uchta o’n yillik ichida ko’p sonli ustvor nazariyalar va usullarning paydo bo’lishiga olib k е ldi. Ulardan noravshan to’plamlar nazariyasini, uning asosida qurilgan imkoniyatlar nazariyasi va noravshan mantiqni, amaliy int е rval tahlil, taqribiy to’plamlar nazariyasini ajratib ko’rsatish mumkin. Ushbu asosiy nazariyalarning ko’pgina zamonaviy ko’rinishlari, shu jumladan r е lyativistik va kvant nazariyalari, noravshan to’plamlarning intuitiv nazariyasi va h.k.lar mavjud. Jumladan yangi yondashuvlar klassik nazariyaviy- ehtimolli uslubiyatni rad etmasdan, aksincha usullarni to’g’ri birlashtirish yo’li bilan amaliy muammolarni anchagina samarali y е chishga imkoniyat yaratgan holda uni to’ldiradilar va k е ngaytiradilar. Noravshan to’plamlar nazariyasi (Fuzzy sets theory)ga 1965 yilda B е rkli Univ е rsit е ti prof е ssori Lotfi Zad е (Lotfi Zadeh) “Information and Control” jurnalida “Fuzzy sets” ishini chop etish orqali asos soldi. “Fuzzy” aniqlovchisi o’zb е k tiliga noravshan, noaniq, noqat'iy kabi tarjima qilinib, yangi nazariya «t е gishli-t е gishli emas», «rost-yolg’on» [35, 36, 37] aniq tushunchalar bilan ish yurituvchi an'anaviy klassik mat е matika va Aristot е l mantig’ini to’ldirish maqsadida kiritilgan. Noravshan to’plam kons е psiyasi, Zad е ning fikricha, haqiqiy dunyoning tizimlarida, ayniqsa odamlarni o’z ichiga olgan gumanistik tizimlarda noo’rin sun'iy aniqlikka erishishni talab qilgan tizimlarning klassik nazariyasiga oid mat е matik usullardan qoniqmaslik [35] hisobiga tug’ilgan. Noravshan to’plamlar nazariyasi 1975 yilda amaliyotda qo’llanilgan bo’lib, bunda Mamdani va Assilian (Mamdani and Assilian)lar oddiy bug’ dvigat е lini boshqarish maqsadida birinchi noravshan hisoblagichni qurganlar [101,129]. 1982 yili Xolmblad va Ostergad (Holmbland and Osregaad) birinchi sanoatga oid noravshan hisoblagichni ishlab chiqishgan bo’lib, u Daniyadagi zavodlarning boshqaruvlaridan birida qo’llanilgan. “Agar-u holda” noravshan lingvistik qoidalarga asoslangan birinchi sanoat hisoblagichining muvaffaqiyati matematiklar va injenerlar o’rtasida noravshan to’plamlar nazariyasiga katta qiziqish uyg’otdi. Bir oz vaqtdan so’ng Bart Kosko (Bart Kosko) tomonidan noravshan approksimasiya teoremasi (Fuzzy Approximation Theorem) isbotlangan bo’lib, unga ko’ra har qanday matematik tizim noravshan mantiqqa asoslangan tizim orqali approksimatsiyalanishi mumkin. Boshqa so ’ z bilan aytganda , tabiiy tildagi “ Agar - u holda ” ko ’ rinishidagi mulohazalar - qoidalar , ularning noravshan to ’ plamlar nazariyasi vositalari yordamida kelgusidagi bayonoti yordamida boshqaruv va identifikatsiyalarda qo ’ llanilgan an ’ anaviy differensial va integral hisoblashlarning murakkab apparatidan foydalanmasdan turib , ixtiyoriy “ kirishlar - chiqish ” bog ’ lanishni xohlaganchalik darajada aniq akslantirish mumkin . Noravshan to ’ plamlarga asoslangan tizimlar texnologik jarayonlarni boshqarish , transportni boshqarish , tibbiy tashxis , texnik tashxis , moliyaviy menejment , birjaviy bashorat , tasvirlarni aniqlash kabi sohalarda ishlab chiqilgan va qo ’ llanilgan . Noravshan mantiqiy chiqarish tizimlarini ishlab chiqishga oid amaliy tajriba ularni loyihalashtirishga ketgan vaqt va xarajatlar an ’ anaviy matematik apparatdan foydalanishga nisbatan ancha kam ekanligi to ’ g ’ risida dalolat beradi , jumladan bunda modellarning zaruriy darajadagi ishchanligiga va shaffofligiga erishiladi . Taqdim etilayotgan ish statistik modellardagi noaniq kattaliklarga ( oraliqli , noravshan va h . k ) asoslangan holda amaliyotda hisoblashlar olib borish masalalariga bag ’ ishlanadi . Asosiy e’tibor modellashtirish, murakkab tizimlarning ishlashini muqobillashtirish va sifatini baholash uchun noravshan to’plamlar va interval tahlil nazariyalarining amaliy ilovalariga qaratilgan. Noravshan to’plamlar nazariyasining asosiy atamalari va tushunchalari bayon etilgan. Asosiy atama va tushunchalar Vaqtning haqiqiy masshtabida masalalarni yechishning xususiyatlari shuni ko’rsatadiki, hisoblash imkoniyatlarining yetishmovchiligi masalaning sharoitlari to’g’risidagi axborotning yetishmasligiga ekvivalent bo’lishiga olib keladi. Universal to’plam bittadan ortiq nuqtaga ega bo’lgandagina [44] ishga ko’ra noaniqlik o’rinlidir. Agar to’plamning ushbu elementlari uchun mos ehtimollar yoki boshqa ehtimolli tavsiflar berilgan bo’lsa, u holda ehtimolli noaniqlik o’rinlidir. Agar to’plamning faqatgina chegeraviy elementlari ma’lum bo’lsa - interval noaniqlik o’rinlidir. Va nihoyat, to’plamning har bir elementi uchun tegishlilik darajasi berilgan bo’lsa - noravshanlik ko’rinishidagi noaniqlik o’rinlidir. Noravshan to’plam tushunchasi - matematik modellarni qurish uchun noravshan ma’lumotni matematik jihatdan bayon etishga harakat qilingan urinishlardir. Ushbu tushunchaning zaminida berilgan to’plamni tashkil qilgan bir xil xususiyatli elementlar shu xususiyatga har xil darajada ega bo’lishi, demak berilgan to’plamga har xil darajada tegishli bo’lishi mumkinligi to’g’risidagi tasavvur yotadi. Bunday yondashuvga asosan “qandaydir element berilgan to’plamga tegishli” ko’rinishidagi mulohazalar ma’noga ega bo’lmay qoladi, chunki aniq bir element berilgan to’plamni qanday darajada yoki “qanchalik kuchli” qoniqtirishini ko’rsatish zarur [35]. U tashuvchi- bu baholanayotgan kvazistatistika doirasidagi kuzatishlarning barcha natijalari tegishli bo’lgan universal to’plamdir. Masalan, agar biz paxtaning hosildorligini kuzatayotgan bo’lsak, u holda tashuvchi - o’lchov birligi senter bo’lgan bir gektardan olinadigan paxta miqdori qo’yilgan haqiqiy o’qdan ajratilgan kesmadir. U universal top’lamdagi ~A noravshan to’plam (fuzzy set) deb ( μ~A,u ) juftliklar majmuiga aytiladi, bunda μ~A - elementning ~A noravshan to’plamga tegishlilik darajasidir. Tegishlilik darajasi - [0, 1] oraliqdagi sondir. Tegishlilik darajasi qanchalik yuqori bo’lsa, universal to’plamning elementi [116,126,152] noravshan to’plamning xossalariga shunchalik ko’proq darajada tegishli bo’ladi. А noravshan to ’ plam – tashuvchining har bir qiymatiga ushbu qiymatning A to ’ plamga tegishlilik darajasi mos qo ’ yilgan tashuvchining qiymatlar to ’ plamidir [107,128]. Masalan : lotin alifbodagi X , Y , Z harflar , albatta , Alphabet = { A , B , C , X , Y , Z } to ’ plamga tegishli va shu nuqtai nazardan Alphabet – ravshan . Lekin “ Paxtaning muqobil hosildorligi ” to ’ plamini tahlil qiladigan bo ’ lsak , u holda 50 s / ga hosildorlik berilgan noravshan to ’ plamga ma ’ lum  darajada tegishli bo ’ lib , uni tegishlilik funksiyasi deb ataydilar . Tegishlilik funksiyasi (membership function) - bu universal to ’ plamdagi ixtiyoriy elementning noravshan to ’ plamga tegishlilik darajasini hisoblashga imkon beruvchi funksiyadir . Agar universal to’plam U ={u1,u2,...,uk} chekli sondagi elementlardan iborat bo’lsa, u holda ~A noravshan to’plam ~A= ∑ j=1 k μ~A(uj)/uj ko’rinishida yoziladi. Uzluksiz U to’plam holida ~A= ∫ [u,u] μ~A(u)/u belgilashdan foydalanishga kelishilgan. Masalan, “paxtaning o’rtacha hosildorligi” tushunchasini noravshan to’plam ko’rinishida quyidagicha tasvirlash mumkin: ~ A = 0/21+0.1/22 + 0.3/23 + 0.8/24 +1/25 +1/26 + 0.5/27 +0/28. 1.1.1-rasmda “Paxtaning hosildorligi” noravshan to’plamining bir qator mutaxassislar o’rtasida so’rov o’tkazish orqali hosil qilingan tegishlilik funksiyasi keltirilgan. 20 30 40 50 60 70 8000.20.40.60.8 1 m( u) u 1.1.1-rasm. Tegishlilik funksiyasining ko’rinishi 20 dan 35 gacha bo’lgan hosildorlik mutaxassislar tomonidan so’zsiz muqobil, 60 va undan yuqoriroq - so’zsiz nomuqobil deb baholandi. 35 dan 60 gacha bo’lgan oraliqda mutaxassislar o’zlarining sinflashtirishlarida noqatiy xulosalarni ko’rsatdilar va bu noqatiylikning tuzilishi tegishlilik funksiyasining grafigida namoyon bo’ldi. Tegishlilik funksiyasini (F-funksiyalarni) qurish masalasi noravshan to’plamlar nazariyasidagi asosiy masalalardan biri bo’lib, bu muammo nafaqat noravshan to’plamlar uchungina muhim hisoblanadi [39]. Tegishlilik funksiyasining aniq ko’rinishi mavjud noaniqlikning haqiqiy holatlarini hisobga olgan holda ushbu funksiyalarning xossalariga oid qo’shimcha farazlar (birinchi tartibli hosilaning simmetrilik, monotonlik, uzluksizlik xossalari) asosida aniqlanadi. Ko’pgina amaliy holatlarda tegishlilik funksiyasi unga oid qismiy axborotdan, aytaylik uning chekli х 1 ,..., х n tayanch nuqtalar to’plamida qabul qilinadigan qiymatlardan kelib chiqqan holda baholanishi kerak. Bunday holatda u “sharxlovchi misol” yordamida qisman aniqlangan deyiladi. 1.1.2-1.1.4-rasmlarda noravshan to’plamlar nazariyasida qo’llaniluvchi tegishlik funksiyasining asosiy ko’rinishlari keltirilgan [18,40]. Simmetrik gauss tegishlilik funksiyasi : μ(x)= e −(x−b)2 2c2 b -3 c b b +3 c 1.1.2-rasm. Simmetrik gauss tegishlilik funksiyasi Qo’ng’iroq ko’rinishidagi umumlashgan tegishlilik funksiyasi: μ(x)= 1 1+|x− c a | 2b 00.20.40.60.8 11.2 00.20.40.60.8 11.2 С 1.1.3-rasm. Qo’ng’iroq ko’rinishidagi umumlashgan tegishlilik funskiyasi Sigmasimon tegishlilik funksiyasi : μ(x)= 1 1+e−a(x−c) 1.1.4-rasm. Sigmasimon tegishlilik funksiyasi . To’plam tashuvchisi, o’tish nuqtasi va singlton. Noravshan to’plamning tashuvchisi μA(x)>0 bo’lgan x elementlardan iboratdir: sup pA = {x∈ X ,μ(x)>0} . μA(x)= 1 2 bo’lgan x∈X element A noravshan to’plamning o’tish nuqtasi deyiladi. Tashuvchisi X dan olingan μA=1.0 bitta nuqta bo’lgan noravshan to’plam singlton deyiladi. Noravshan to’plamning balandligi, normal noravshan to’plam. A noravshan to’plamning balandligi deb tegishlilik funksiyasining eng yuqori chegarasiga aytiladi: hgt (A)= sup x∈X μA(x) . Foydalanilgan adabiyotlar 1. Muhamediyeva D.T. Noravshan axborot holatida sust shakllangan jarayonlarni modellashtirish. Toshkent: O’zR FA matematika va axborot texnologiyalar instituti, 2010. 37 ta jadval, 87 ta rasm, 155 ta bibl.atama, 400 bet. 2. Артикова С., Мухамедиева Д.Т. Информатизация регулирования развития экономики Республики // Известия ВУЗов. –Т., 2000. №3. 3. Артикова С., Мухамедиева Д.Т. Реализация моделей принятия решений с учетом информационых ситуаций //Узбекский журнал энергетики и информатики.-Т. ,2000. №3. 4. Ахмедов Т.М. Мухамедиева Д.Т. Шодмонова У.А. Рациональное управление распределением и использованием ресурсов в условиях рыночной экономики. Доклады международной конференции «Устойчивое экономическое развитие и эффективное управление ресурсами в Центральной Азии». ТГЭУ и Ноттенгемский Трент Университет (Великобритания). Ташкент-Ноттенгем. 2001. –С.14-17. 00.20.40.60.8 11.2 Mavzu: Noravshan t o’plamning xususyat lari Re ja: K irish 1. Noravshan t o’plamning quvvat i. 2. Noravshan qismga agrat ish 3. Trape siya k o’rinishidagi (Trape siyasimon) noravshan son Foydalanilgan adabiyot lar Kirish . Keyingi boblarda ko’rilgan masalalarning qo’yilishini tushunish uchun zarur bo’lgan hajmda imkoniyatlar nazariyasi, amaliy interval tahlil, noravshan to’plamlar nazariyasining asosiy holatlari keltirilgan. Noravshanlik, ehtimollik va imkoniyat o’rtasidagi o’zaro bog’lanishlar va cheklanishlarning muhim uslubiy muammolari ko’rib chiqilgan. Oraliqli va noravshan-oraliqli matematikalar o’rtasidagi chuqur bog’lanish ko’rsatilgan. Noaniqliklarni boshqarishning amaliy qo’llash uchun anchagina qulay hisoblangan bir qator zamoanviy usullariga qisqa tavsiflar keltirilgan. Oxirgi boblarda bayon etilgan aniq amaliy misollarda noaniq sharoitlarda paxta ishlab chiqarish masalalarini yechishda noravshan to’plamlar nazariyasini qo’llashning ustuvorliklari ko’rsatilgan. Har bir masala uchun hisoblash algoritmi keltirilgan bo’lib, noravshan kattaliklar bilan ishlash paytida olinadigan haqiqiy yoki gipotetik ma’lumotlarga oid natijalar ko’rsatilgan. Kitob nafaqat o’zining sohasida modellashtirish va muqobillashtirish masalalari bilan bevosita bog’liq bo’lgan o’quvchilarni, balki ishlab chiqaruvchilarni, sog’liqni saqlash xodimlarini, iqtisodchilarni, moliyachilarni, ekologlar va boshqaruv organlarining xodimlarini o’ziga jalb etishi mumkin. Noravshan to’plamning quvvati. X -chekli to’plam va A - X da aniqlangan noravshan to’plam bo’lsin. U holda A noravshan to’plamning |A| quvvati quyidagicha aniqlanadi: |A|= ∑ x∈X μA(x) . X -cheksiz to’plam holida, |A| har doim ham mavjud bo’lavermaydi. Lekin, agar A chekli tashuvchiga ega bo’lsa, u holda A noravshan to’plamning quvvati quyidagicha aniqlanadi: |A|= ∑ x∈sup pA μA(x) . A noravshan to’plam B noravshan to’plamga tegishli (А⊆В) deyiladi, faqat va faqat ∀ x∈X , μA(x)≤ μB(x) bo’lsa. Tengsizlik qat’iy bo’lsa, tegishlilik qat’iy hisoblanib, A⊂B orqali belgilanadi. x α darajali A ga tegishli bo’ladi, faqat va faqat x∈A bo’lsa, Aα B ga sust tegishli bo’ladi ( A− ¿αB ), agar X ning barcha elementlari α darajada ¯A yoki B ga tegishli bo’lsa, matematik ko’rinishda esa A− ¿αB , agar x∈(¯A∪ B)α ∀ x∈X yoki ∀ x∈X , max (1− μA(x),μB(x))≥α . A>− −¿B sust tenglama quyidagicha aniqlanadi: μA(x) va μB(x) tegishlilik belgilari ½ dan yoki katta yoki teng, yoki ikkalasi ½ dan kichik yoki teng. A>− −¿B , faqat va faqat ∀ x∈X ,min [max (1− μA(x),μB(x)),min (1− μA(x),1−μB(x))]≥1/2 bo’lsa. Kartezian ko’paytma . Agar A1,...,An mos ravishda U1,...,Un dagi norvashan to’plamlar bo’lsa, A1,...,An kartezian ko’pyatma U1×U2×...×Un fazodagi μ A1×...× An(u 1,u 2,...,u n)= min ¿ ¿ ¿ yoki μA1×...×An(u1,u2,...,un)= μA1(u1)⋅μA2(u2)⋅...⋅μAn(un) tegishlilik funksiyali noravshan to’plam bo’ladi. Noravshan qismga agratish. Agar A to’plam X ning oddiy qism to’plami bo’lsa, u holda (A,¯A) juftlik A≠∅ ,A≠ X shartni qanoatlantiruvchi X to’plamning bo’linishidir. Agar A noravshan to’plam bo’lsa, ( A≠∅ ,A≠ X ) u holda (A,¯A) juftlik noravshan qismga ajratish deyiladi. Agar noravshan to’plamlar tizimi A1,...,Am (Ai≠ ∅ ,Ai≠ Xi,i=1,m) ∀ x∈X ,∑i=1 N μAi(x)=1shartni qanoatlantirsa, u holda tizim X to’plamning noravshan qismlari deyiladi . Defazzifiikasiya (defuzzification) deb noravshan to’plamni ravshan songa keltiruvchi jarayonga aytiladi [86,87]. Noravshan to’plamlar nazariyasida defazzifikasiya jarayoni ehtimollar nazariyasida tasodifiy sonlar vaziyatlarining tavsiflarini (matematik kutish, modalar, medianlar) topish kabidir. Defazzifikasiya jarayonini bajarishning eng sodda usuli tegishlilik funksiyasining maksimumiga mos ravshan sonni tanlashdan iboratdir. Lekin bu usulning qo’llanilish chegarasi bir ekstremalli tegishlilik funksiyalari bilan cheklanib qoladi. Ko’p ekstremmalli tegishlilik funksiyalari uchun defazzifikasiyaning quyidagi usullari hisobga olingan: Centroid – og’irlik markazi; Bisector - mediana; LOM (Largest Of Maximums) –maksimumlar ichida eng kattasi; SOM (Smallest Of Maximums) – maksimumlar ichida eng kichigi; Mom (Mean Of Maximums) –maksimumlar markazi. ~A= ∫ [u,u] μ~A(u)/u noravshan to’plamni og’irlik markazi usulida defazzifikasiyalash quyidagi formula bo’yicha amalga oshiriladi: a= ∫ u u u⋅μ~A(u)du ∫ u u μ~A(u)du . Ushbu formulaning fizik ko’rinishi koordinatalar o’qi va noravshan to’plamning tegishlilik funksiyalari bilan chegaralangan tekis figuraning og’irlik markazini topishdan iboratdir. Diskret universal to’plam holida noravshan to’palmni og’irlik markazi usulida defazzifikasiyalash a= ∑ j=1 k uj⋅μ~A(uj) ∑ j=1 k μ~A(uj)formula bo’yicha amalga oshiriladi. ~A= ∫ [u,u] μ~A(u)/u noravshan to’plamni mediana usulida defazzifikasiyalash uchun ∫ u a μ~A(u)du =∫ a ¯u μ~A(u)du tenglikni qanoatlantiradigan a sonni topish zarur. Mediana usulining geometrik talqini absissalar o’qida shunday nuqtani topishdan iboratki, shu nuqtadan o’tkazilgan perpendikulyar tegishlilik funksiyasi egri chizig’ining ostidagi yuzani ikkita teng qismga ajratsin. ~A= ∫ [u,u] μ~A(u)/u noravshan to’plamni maksimumlar markazi yordamida defazzifikasiyalash a= ∫ G udu ∫ G du formula bo’yicha amalga oshiriladi. Bu yerda G - noravshan to’plamga [u,u] oraliqdan maksimal darajada tegishli bo’lgan barcha elementlar to’plami. Maksimumlar markazi usulida defazzifikasiyalash tegishlilik darajasi maksimal bo’lgan universal to’plamdagi elementlarning o’rta arifmetigi kabi aniqlanadi. Agar bunday elementlar to’plami chekli bo’lsa, u holda formula quyidagi ko’rinishga keladi: a= ∑ uj∈G uj |G | , bu yerda |G| - G to’plamning quvvati. Diskret holatda maksimumlar ichida eng katta va maksimumlar ichida eng kichkina usullari bo’yicha defazzifikasiyalash mos ravishda a= max (G) va a= min (G ) formulalari bo’yicha amalga oshiriladi. Oxirgi uchta formulalardan shu narsa ayon bo’ladiki, tegishlilik funksiyasi bittagina maksimumga ega bo’lsa, uning koordinatasi [76,84,133] noravshan to’plamning aniq nusxasidir. Masalan, “paxtaning o’rtacha hosildorligi” noravshan to’plamini og’irlik markazi usulida defazzifikasiyalash mumkin. Og’irlik markazi usuli bo’yicha noravshan to’plamni defazzifikasiyalash formulasini qo’llagan holda a= 0⋅21 +0.1⋅22 +0.3⋅23 +0.8⋅24 +1⋅25 +1⋅26 +0.5⋅27 +0⋅28 0+0.1+0.3+0.8+1+1+0.5+0 =25.08 ga ega bo’lamiz. Noravshan son – normal va qavariq, ya’ni a) tegishlilik funskiyasi birga teng bo’lgan tashuvchining qiymatiga ega bo’lgan b) maksimumidan chapga yoki o’ngga siljiganda kamayadigan tegishlilik funksiyasiga ega bo’lgan haqiqiy sonlar universal to’plamining noravshan qism to’plamidir [113,114,145]. Keyinchalik bizga kerak bo’ladigan noravshan sonlarni ko’rib chiqaylik. Trapesiya ko’rinishidagi (Trapesiyasimon) noravshan son . Ma’lum bir kvazistatistikani o’rganib chiqamiz va  = « U o’zgaruvchining qiymati» deb olamiz, bu yerda U – kvazistatistika tashuvchilarining qiymatlar to’plami. Qiymatlarning ikkita term-to’plamini ajratamiz: М 1 noravshan qism to’plamli T 1 = « U taxminan a dan b gacha bo’lgan oraliqda yotibdi» va М 2 noravshan qism to’plamli sarlavhasiz T 2 to’plam, jumladan bu yerda М 2 =  М 1 shart bajariladi. U holda  T1 (u) tegishlilik funksiyasi 1.1.9 rasmdagi kabi ko’rinishga ega bo’ladi. 0 0.2 0. 4 0.6 0. 8 1 1. 2 1. 4 0 0. 2 0. 4 0. 6 0. 8 1 1. 2 a1 a2 a3 a41.1.9-rasm. Trapesiyasimon noravshan sonning tegishlilik funksiyasi Oraliqning chegaralari noravshan tarzda berilgani uchun, trapesiya uchlarining absissalarini quyidagi ko’rinishda kiritish maqsadga muvofiqdir: а = ( а 1 + а 2 )/2, в = ( в 1 + в 2 )/2, jumladan а 1 , а 2 va в 1 , в 2 uchlar bir biriga nisbatan “taxminan” tushunchasiga qanday mazmun berishimizga qarab joylashadilar: kvazistatistikaning taxmini qanchalik katta bo’lsa, trapesiyaning yon qirralari shunchalik taxminiy bo’ladi. Chegaralangan holda “taxminan” tushunchasi “ixtiyoriy joyda” tushunchasiga aylanadi. Agar biz o’zgaruvchini sifat jihatidan baholaydigan bo’lsak, “Bu qiymat o’rtacha hisoblanadi” deb fikr bildirgandan so’ng ekspert bahosi (noravshan sinflashtirishning) “O’rtacha qiymat - bu taxminan a dan b gacha” kabi aniqlashtiruvchi tasdig’ini kiritib, so’ngra esa noravshan sinflashtirishni modellashtirishda trapesiyasimon sonlarni ishlatish mumkin. Aslida bu ishonchsiz sinflashtirishning eng tabiiy usulidir. Uchburchak noravshan sonlar . Endilikda huddi o’sha lingvistik o’zgaruvchi uchun Т 1 ={ U taxminan a ga teng} term-to’plamni kiritamiz. а    а ligi ravshan, jumladan  ning nolga qarab Foydalanilgan adabiyotlar 1. Muhamediyeva D.T. Norav shan axborot hol at i da sust shak l l angan j aray onl arni modell asht i ri sh. Toshkent: O’zR FA matematika va axborot texnologiyalar instituti, 2010. 37 ta jadval, 87 ta rasm, 155 ta bibl.atama, 400 bet. 2. Артикова С., Мухамедиева Д.Т. Информатизация регулирования развития экономики Республики // Известия ВУЗов. –Т., 2000. №3. 3. Артикова С., Мухамедиева Д.Т. Реализация моделей принятия решений с учетом информационых ситуаций //Узбекский журнал энергетики и информатики.-Т. ,2000. №3. 4. Ахмедов Т.М. Мухамедиева Д.Т. Шодмонова У.А. Рациональное управление распределением и использованием ресурсов в условиях рыночной экономики. Доклады международной конференции «Устойчивое экономическое развитие и эффективное управление ресурсами в Центральной Азии». ТГЭУ и Ноттенгемский Трент Университет (Великобритания). Ташкент-Ноттенгем. 2001. –С.14-17. Mavzu: Noravshan t o’plamlarning arif me t ik asi Re ja: K irish 1. Noravshan t o’plamlarning alge braik yig’indisi 2. Noravshan t o’plamlarning che k langan yig’indisi Foydalanilgan adabiyot lar Kirish Noravshan to’plam kons е psiyasi, Zad е ning fikricha, haqiqiy dunyoning tizimlarida, ayniqsa odamlarni o’z ichiga olgan gumanistik tizimlarda noo’rin sun'iy aniqlikka erishishni talab qilgan tizimlarning klassik nazariyasiga oid mat е matik usullardan qoniqmaslik [35] hisobiga tug’ilgan. Noravshan to’plamlar nazariyasi 1975 yilda amaliyotda qo’llanilgan bo’lib, bunda Mamdani va Assilian (Mamdani and Assilian)lar oddiy bug’ dvigat е lini boshqarish maqsadida birinchi noravshan hisoblagichni qurganlar [101,129]. 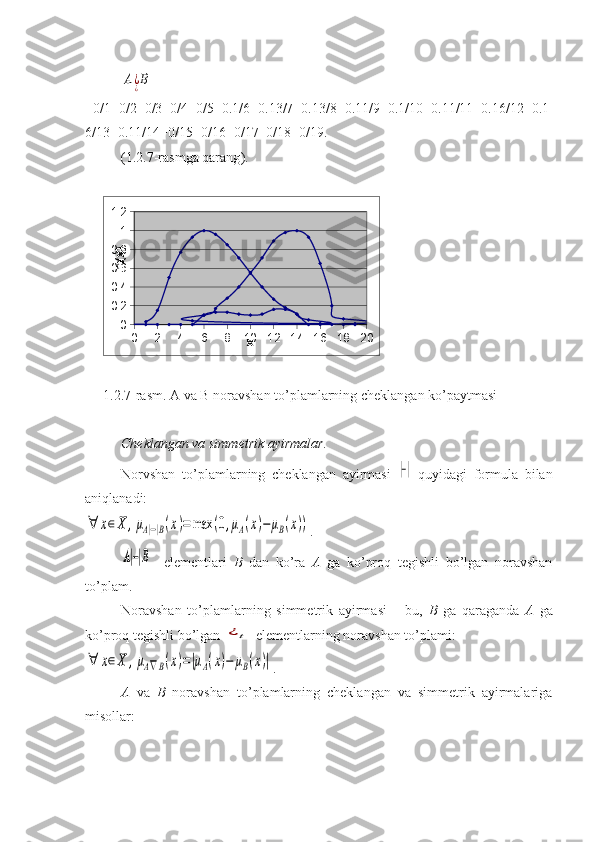А va В – X dagi mos ravishda μA va μB tegishlilik funksiyali ikkita noravshan to’plam bo’lsin. A va B noravshan to’plamlarning cheklangan ko’paytmasi amali ularning tegishlilik funksiyalariga qarab, quyidagi tarzda aniqlanadi. А va В – X dagi mos ravishda μA va μB tegishlilik funksiyali ikkita noravshan to’plam bo’lsin. A va B noravshan to’plamlarning algebraik yig’indisi amali ularning tegishlilik funksiyalariga qarab, quyidagi tarzda aniqlanadi: A=0.03/1+0.1/2+0.28/3+0.52/4+0.75/5+0.94/6+1/7+0.96/8+0.87/9+ +0.71/10+0.55/11+0.4/12+0.28/13+0.19/14+0.12/15+0.06/16+0.02/17, B=0/1+0/2+0/3+0.02/4+0.06/5+0.12/6+0.17/7+0.25/8+0.35/9+0.5/10+ +0.68/11+0.82/12+0.95/13+1/14+0.95/15+0.62/16+0.35/17+ +0.17/18+0.06/19, A^+¿B¿ =0.03/1+0.1/2+0.28/3+0.52/4+0.75/5+0.94/6+1.0/7+0.96/8+ +0.91/9+0.86/10+0.86/11+0.88/12+0.96/13+1.0/14+0.95/15+ +0.62/16+0.35/17+0.17/18+0.06/19. (1.2.5-rasmga qarang ). 0 2 4 6 8 10 12 14 16 18 2000.20.40.60.8 11.2 x m(x) 1.2.5-rasm . Noravshan to’plamlarning algebraik yig’indisi А va В – X dagi mos ravishda μA va μB tegishlilik funksiyali ikkita noravshan to’plam bo’lsin. A va B noravshan to’plamlarning chegaralangan yig’indisi amali ularning tegishlilik funksiyalariga qarab quyidagi tarzda aniqlanadi: A=0.06/1+0.17/2+0.31/3+0.5/4+0.67/5+0.82/6+0.93/7+1.0/8+0.98/9+ +0.89/10+0.75/11+0.6/12+0.45/13+0.33/14+0.23/15+0.14/16+ +0.08/17+0.03/18, B=0.03/4+0.08/5+0.15/6+0.26/7+0.4/8+0.55/9+0.7/10+0.85/11+ +0.95/12+1/0/13+0.96/14+0.85/15+0.6/16+0.33/17+0.18/18+0.09/19, A ˙¿B =0.06/1+0.17/2+0.31/3+0.53/4+0.75/5+0.97/6+1.0/7+1.0/8+1.0/9+ +1.0/10+1.0/11+1.0/12+1.0/13+1.0/14+1.0/15+0.64/16+0.41/17+ +0.21/18+0.09/19. ( 1.2.6-rasmga qarang ). 0 2 4 6 8 10 12 14 16 18 20 0 0.2 0.4 0.6 0.8 1 1.2 x m(x) 1.2.6 -rasm. Noravshan to’plamlarning cheklangan yig’indisi A=0.03/1+0.15/2+0.5/3+0.77/4+0.93/5+1.0/6+0.96/7+0.85/8+0.71/9+ +0.55/10+0.4/11+0.27/12+0.18/13+0.11/14+0.05/15+0.01/16, B=0.04/5+0.1/6+0.17/7+0.28/8+0.4/9+0.55/10+0.71/11+0.89/12+0.98/13+ +1.0/14+0.93/15+0.65/16+0.2/17+0.06/18+0.01/19, A¿¿B=0/1+0/2+0/3+0/4+0/5+0.1/6+0.13/7+0.13/8+0.11/9+0.1/10+0.11/11+0.16/12+0.1 6/13+0.11/14+0/15+0/16+0/17+0/18+0/19. ( 1.2.7-rasmga qarang ) . 0 2 4 6 8 10 12 14 16 18 2000.20.40.60.8 11.2 x m (x) 1.2.7 -rasm. A va B noravshan to’plamlarning cheklangan ko’paytmasi Cheklangan va simmetrik ayirmalar. Norvshan to’plamlarning cheklangan ayirmasi |−| quyidagi formula bilan aniqlanadi: ∀ x∈X ,μA|−|B(x)= max (0,μA(x)− μB(x)) . A|−|B elementlari B dan ko’ra A ga ko’proq tegishli bo’lgan noravshan to’plam. Noravshan to’plamlarning simmetrik ayirmasi – bu, B ga qaraganda A ga ko’proq tegishli bo’lgan ¿t elementlarning noravshan to’plami: ∀ x∈X ,μA∇B(x)=|μA(x)− μB(x)| . 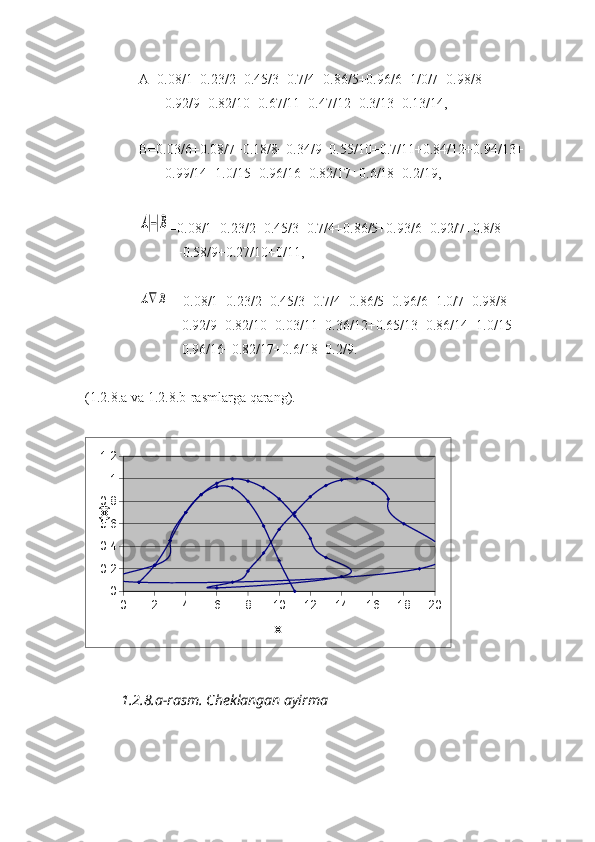A va B noravshan to’plamlarning cheklangan va simmetrik ayirmalariga misollar : A=0.08/1+0.23/2+0.45/3+0.7/4+0.86/5+0.96/6+1/0/7+0.98/8+ +0.92/9+0.82/10+0.67/11+0.47/12+0.3/13+0.13/14, B=0.03/6+0.08/7+0.18/8+0.34/9+0.55/10+0.7/11+0.84/12+0.94/13+ +0.99/14+1.0/15+0.96/16+0.82/17+0.6/18+0.2/19,A|−|B =0.08/1+0.23/2+0.45/3+0.7/4+0.86/5+0.93/6+0.92/7+0.8/8+ +0.58/9+0.27/10+0/11, А∇ В =0.08/1+0.23/2+0.45/3+0.7/4+0.86/5+0.96/6+1.0/7+0.98/8+ 0.92/9+0.82/10+0.03/11+0.36/12+0.65/13+0.86/14+1.0/15+ 0.96/16+0.82/17+0.6/18+0.2/9. (1.2.8. а va 1.2.8.b-rasmlarga qarang ). 0 2 4 6 8 10 12 14 16 18 2000.20.40.60.8 11.2 x m (x) 1.2.8. а -rasm. Cheklangan ayirma 0 2 4 6 8 10 12 14 16 18 2000.20.40.60.8 11.2 xm(x) 1.2.8.b-rasm. Simmetrik ayirma A noravshan to’plamning m-darajasi quyidagiga teng: μAm(x)= [μA(x)]m, ∀ x∈ X ,∀ m ∈R+ , bu yerda R+ - musbat aniqlangan haqiqiy sonlar to’plami. Noravshan to’plamlar konsentrasiyasi, kengaytmasi . A quyidagi universumda noravshan to’plam bo’lsin: A= {(x:μA(x))|x∈ X } . U holda Con m konsentrasiyalash amali yordamida darajaga ko’tarish natijasida hosil bo’ladigan noravshan to’plamlar Con mA= {(x:(μA(x))m)|x∈ X } A ning konsentrasiyalari, kengaytma amali yordamida ildiz olish dil nA= {(x:n√μA(x))|x∈X } esa A ning kengaytmalari deyiladi. Natija . [μA(x)]n≤ μA(x)≤n√μA(x) ifoda hamma x∈X larda haqiqiy bo’lsa va n>1 bo’lsa, u holda Con nA⊂A⊂dil nA qism to’plamlarning munosabati ham haqiqiy hisoblanadi. +0.22/18+0.15/19 ( 1.2.10-rasmga qarang ). 0 2 4 6 8 10 12 14 16 18 2000.20.40.60.8 11.2 x m (x) 1.2.10-rasm . Noravshan to’plamlarning kengaytmasi Noravshan to’plamlarni konsentrasiya va kengaytma amallaridan foydalangan holda almashtirish misollari quyida keltirilgan [6]. А = ∫ μA(x)/x Juda А = ∫ [μA(x)] 2/x Juda juda А = ∫ [μA(x)] 4/x Bir muncha А = ∫ √μA(x)/x Ozgina А = ∫ 4√μA(x)/x А emas = ∫(1−μA(x))/x Uncha А emas =∫ (1−[μA(x)] 2)/x Noravshan nuqtalar, noravshan oraliqlar, noravshan sohalar . Foydalanilgan adabiyotlar 5. Muhamediyeva D.T. Noravshan axborot holatida sust shakllangan jarayonlarni modellashtirish. Toshkent: O’zR FA matematika va axborot texnologiyalar instituti, 2010. 37 ta jadval, 87 ta rasm, 155 ta bibl.atama, 400 bet. 6. Артикова С., Мухамедиева Д.Т. Информатизация регулирования развития экономики Республики // Известия ВУЗов. –Т., 2000. №3. 7. Артикова С., Мухамедиева Д.Т. Реализация моделей принятия решений с учетом информационых ситуаций //Узбекский журнал энергетики и информатики.-Т. ,2000. №3. 8. Ахмедов Т.М. Мухамедиева Д.Т. Шодмонова У.А. Рациональное управление распределением и использованием ресурсов в условиях рыночной экономики. Доклады международной конференции «Устойчивое экономическое развитие и эффективное управление ресурсами в Центральной Азии». ТГЭУ и Ноттенгемский Трент Университет (Великобритания). Ташкент-Ноттенгем. 2001. –С.14-17. Mavzu: Noravshan t o’plamlar ust ida amallar Re ja: Kirish. 1. Noravshan t o’plamlar ust ida amallar 2. Noravshan t o’plamlarning birlashmasi 3. Noravshan t o’plamlarning alge braik y ig’indisi Kirish. Noravshan to’plam kons е psiyasi, Zad е ning fikricha, haqiqiy dunyoning tizimlarida, ayniqsa odamlarni o’z ichiga olgan gumanistik tizimlarda noo’rin sun'iy aniqlikka erishishni talab qilgan tizimlarning klassik nazariyasiga oid mat е matik usullardan qoniqmaslik [35] hisobiga tug’ilgan. Noravshan to’plamlar nazariyasi 1975 yilda amaliyotda qo’llanilgan bo’lib, bunda Mamdani va Assilian (Mamdani and Assilian)lar oddiy bug’ dvigat е lini boshqarish maqsadida birinchi noravshan hisoblagichni qurganlar [101,129]. Noravshan to’plamlar ustida amallar Klassik to’plamlar uchun quyidagi amallar kiritilgan: To’plamlarning kesishmasi – A va B to’plamlardagi ham A , ham B to’plamga tegishli elementlardan iborat bo’lgan С = А  В to’plamidir. To’plamlarning birlashmasi - A va B to’plamlardagi yoki A , yoki B , yoki ikkala to’plamga tegishli elementlardan iborat bo’lgan С = А  В to’plamidir. To’plamlarning inkori - universal to’plamga tegishli, lekin A to’plamga tegishli bo’lmagan elementlarni o’z ichida mujassamlashtirgan С =  А to’plamidir . Zade shu to’plamlarning tegishlilik funksiyalari amallari yordamida noravshan to’plamlar ustidagi shu kabi amallar majmuini taklif qildi [35]. Shunday qilib, A to’plam  А (u), В to’plam esa  В (u) funksiya orqali berilgan bo’lsa, u holda natija bo’lib  С (u) tegishlilik funksiyali C to’plam hisoblanadi. 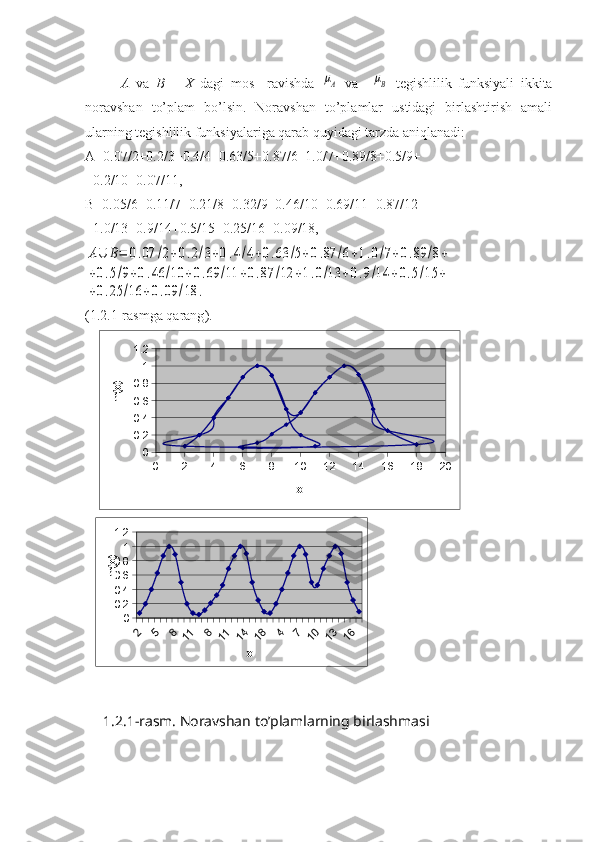Birlashma. A va B noravshan to’plamlarning birlashmasi quyidagi tarzda aniqlanadi: ∀ x∈ X ,μA∪B(x)= max {μA(x),μB(x)} , bu yerda μA∪B - A va B uchun tegishlilik funksiyasi. 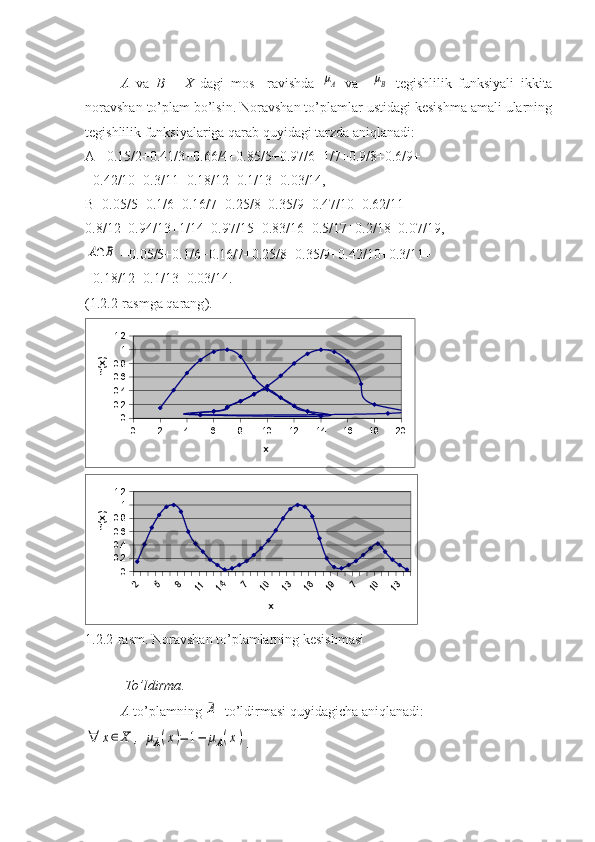Kesishma . μA∩B tegishlilik funksiyasi quyidagicha aniqlanadi: ∀ x∈ X ,μA∩B(x)= min {μA(x),μB(x)} . А va В – X dagi mos ravishda μA va μB tegishlilik funksiyali ikkita noravshan to’plam bo’lsin. Noravshan to’plamlar ustidagi birlashtirish amali ularning tegishlilik funksiyalariga qarab quyidagi tarzda aniqlanadi: A=0.07/2+0.2/3+0.4/4+0.63/5+0.87/6+1.0/7+0.89/8+0.5/9+ +0.2/10+0.07/11, B=0.05/6+0.11/7+0.21/8+0.32/9+0.46/10+0.69/11+0.87/12+ +1.0/13+0.9/14+0.5/15+0.25/16+0.09/18, A∪ B= 0.07 /2+0.2/3+0.4/4+0.63 /5+0.87 /6+1.0/7+0.89 /8+ +0.5/9+0.46 /10 +0.69 /11 +0.87 /12 +1.0/13 +0.9/14 +0.5/15 + +0.25 /16 +0.09 /18 . (1.2.1-rasmga qarang ). 0 2 4 6 8 10 12 14 16 18 20 0 0.2 0.4 0.6 0.8 1 1.2 x m(x) 2 5 8 11 8 11 14 18 4 7 10 13 16 0 0.2 0.4 0.6 0.8 1 1.2 x m(x) 1.2.1-rasm. Noravshan to’plamlarning birlashmasi А va В – X dagi mos ravishda μA va μB tegishlilik funksiyali ikkita noravshan to’plam bo’lsin. Noravshan to’plamlar ustidagi kesishma amali ularning tegishlilik funksiyalariga qarab quyidagi tarzda aniqlanadi: A= 0.15/2+0.41/3+0.66/4+0.85/5+0.97/6+1/7+0.9/8+0.6/9+ +0.42/10+0.3/11+0.18/12+0.1/13+0.03/14, B=0.05/5+0.1/6+0.16/7+0.25/8+0.35/9+0.47/10+0.62/11+ 0.8/12+0.94/13+1/14+0.97/15+0.83/16+0.5/17+0.2/18+0.07/19, A∩ B =0.05/5+0.1/6+0.16/7+0.25/8+0.35/9+0.42/10+0.3/11+ +0.18/12+0.1/13+0.03/14. (1.2.2-rasmga qarang ). 0 2 4 6 8 10 12 14 16 18 2000.20.40.60.8 11.2 x m(x) 2 5 8 11 14 7 10 13 16 19 7 10 13 00.20.40.60.8 11.2 x m(x) 1.2.2 -rasm. Noravshan to’plamlarning kesishmasi To’ldirma . A to’plamning ¯А to’ldirmasi quyidagicha aniqlanadi : ∀ x∈ X , μ¯A(x)= 1− μA(x) . А va В – X dagi mos ravishda μA va μB tegishlilik funksiyali ikkita noravshan to’plam bo’lsin. Noravshan to’plamlar ustidagi to’ldirish amali ularning tegishlilik funksiyalariga qarab quyidagi tarzda aniqlanadi: A=0/1+0.05/2+0.14/3+0.27/4+0.5/5+0.76/6+0.93/7+1.0/8+0.96/9+0.84/10+ +0.62/11+0.37/12+0.25/13+0.16/14+0.09/15+0.03/16+0/17, ¯A =1.0/1+0.95/2+0.86/3+0.73/4+0.5/5+0.24/6+0.07/7+0/8+0.04/9+0.16/10+ +0.38/11+0.63/12+0.75/13+0.84/14+0.91/15+0.97/16+1.0/17. (1.2.3-rasmga qarang). Noravshan to’plamlarning birlashmasi va kesishmasi uchun boshqa amallardan ham foydalanish mumkin. Algebraik ko’paytma: ∀ x∈ X ,μA⋅B(x)= μA(x)⋅μB(x) . Cheklangan ko’paytma: ∀ x∈ X ,μA⊗B(x)= max {0,μA(x)+μB(x)− 1} . 0 2 4 6 8 10 12 14 16 18 0 0.2 0.4 0.6 0.8 1 1.2 x m(x) 1 3 5 7 9 11 13 15 17 2 4 6 8 10 12 14 16 0 0.2 0.4 0.6 0.8 1 1.2 x m(x01.2.3-rasm. Noravshan to’plamning to’ldirmasi Qat’iy (drastic) ko’paytma: μ A intersect ¿ B ( x ) = ¿ ¿ ¿ ¿ ¿ Algebraik yig’indi: ∀ x∈X ,μA+B(x)= μA(x)+μB(x)− μA(x)⋅μB(x) . Cheklangan yig’indi: ∀ x∈X ,μA˙¿B(x)=min {1,μA(x)+μB(x)} . Qat’iy (drastic) yig’ind: μ A ∪+ B ( x ) = ¿ ¿ ¿ ¿ ¿ А va В – X dagi mos ravishda μA va μB tegishlilik funksiyali ikkita noravshan to’plam bo’lsin. A va B noravshan to’plamlarning algebraik ko’paytmasi amali ularning tegishlilik funksiyalariga qarab quyidagi tarzda aniqlanadi: A=0.1/1+0.24/2+0.4/3+0.63/4+0.82/5+0.94/6+1.0/7+0.98/8+0.91/9+0.76/10 +0.57/11+0.35/12+0.2/13+0.1/14+0.04/15, B=0.02/4+0.09/5+0.2/6+0.32/7+0.46/8+0.61/9+0.76/10+0.88/11+0.96/12+ +1.0/13+0.96/14+0.85/15+0.62/16+0.37/17+0.2/18+0.09/19, А∗В=0/3+0.01/4+0.07/5+0.19/6+0.32/7+0.45/8+0.55/9+0.58/10+0.5/11+ +0.34/12+0.2/13+0.96/14+0.03/15+0/16. (1.2.4-rasmga qarang ). 0 2 4 6 8 10 12 14 16 18 20 0 0.2 0.4 0.6 0.8 1 1.2 x m(x) 1.2.4-rasm. Noravshan to’plamlarning algebraik ko’paytmasi А va В – X dagi mos ravishda μA va μB tegishlilik funksiyali ikkita noravshan to’plam bo’lsin. A va B noravshan to’plamlarning algebraik yig’indisi amali ularning tegishlilik funksiyalariga qarab, quyidagi tarzda aniqlanadi: A=0.03/1+0.1/2+0.28/3+0.52/4+0.75/5+0.94/6+1/7+0.96/8+0.87/9+ +0.71/10+0.55/11+0.4/12+0.28/13+0.19/14+0.12/15+0.06/16+0.02/17, B=0/1+0/2+0/3+0.02/4+0.06/5+0.12/6+0.17/7+0.25/8+0.35/9+0.5/10+ +0.68/11+0.82/12+0.95/13+1/14+0.95/15+0.62/16+0.35/17+ +0.17/18+0.06/19, A^+¿B¿ =0.03/1+0.1/2+0.28/3+0.52/4+0.75/5+0.94/6+1.0/7+0.96/8+ +0.91/9+0.86/10+0.86/11+0.88/12+0.96/13+1.0/14+0.95/15+ +0.62/16+0.35/17+0.17/18+0.06/19. (1.2.5-rasmga qarang ). Foydalanilgan adabiyotlar 5. Muhamediyeva D.T. Noravshan axborot holatida sust shakllangan jarayonlarni modellashtirish. Toshkent: O’zR FA matematika va axborot texnologiyalar instituti, 2010. 37 ta jadval, 87 ta rasm, 155 ta bibl.atama, 400 bet. 6. Артикова С., Мухамедиева Д.Т. Информатизация регулирования развития экономики Республики // Известия ВУЗов. –Т., 2000. №3. 7. Артикова С., Мухамедиева Д.Т. Реализация моделей принятия решений с учетом информационых ситуаций //Узбекский журнал энергетики и информатики.-Т. ,2000. №3. 8. Ахмедов Т.М. Мухамедиева Д.Т. Шодмонова У.А. Рациональное управление распределением и использованием ресурсов в условиях рыночной экономики. Доклады международной конференции «Устойчивое экономическое развитие и эффективное управление ресурсами в Центральной Азии». ТГЭУ и Ноттенгемский Трент Университет (Великобритания). Ташкент-Ноттенгем. 2001. –С.14-17. NORA VSHA N MUNOSA BA TLA R VA ULA RNI NG HUSUSY A TLA RI Re ja: Kirish 1. Noravshan munosabat lar va noravshan che k lanishlar 2. Noravshan ma’lumot ning t ashuvchisi F oy dalanilgan adabiy ot Kirish “Munosabat” atamasi bir xil X universumda berilgan ayrim akslantirishlar turlarini belgilash uchun ishlatiladi. Bunday holatdaRα={(u,v)/(u,v)∈X×X,μR(u,v)≥α} akslantirish X to’plamdan o’z-o’ziga akslantirish bo’lib, u { Х , Г } juftlik orqali aniqlanadi, bu yerda Г ⊆X2 [35]. X2 to’plamning elementlari tartiblangan juftliklar bo’lganligi uchun, munosabat - bu tartiblangan juftliklarning to’plamidir, chunki har bir juftlik X2 to’plamning faqatgina 2 ta elementlari orqali o’zaro birlashtiriladi. Bunday munosabat binar munosabat deb ataladi. Agar Xn to’plamning elementlari tartiblangan n -tali juftliklar bo’lsa, bunday munosabat n -tali munosabat deb ataladi. Xususiy hol - ternar munosabat - tartiblangan uchliklardan iborat to’plam. Norav shan munosabat lar v a norav shan chek lanishlar Noravshan munosabat tushunchasi - ravshan munosabatlarning noravshan to’plamlar nazariyasidagi umumlashmasidir. U elementlar o’rtasidagi o’zaro ta’sir bir oz kuchli bo’lgan holatlarni modellashtirishi mumkin. Munosabatlarning har xil turlarini farqlash mumkin. Masalan, tartib, ustuvorlik, ekvivalentlik va h.k. munosabatlar. x1,x2,...xn to’plamlardagi ~R noravshan munosabat d е b x1×x2×...×xn d е kart ko’paytmaning noravshan qism to’plamiga aytiladi. μ~R(x1,x2,...,xn) t е gishlilik funksiyasi ~R munosabatning ( x1,x2,...xn ) xi∈Xi , i=1,n el е m е ntlar orasida bajarilish darajasini bildiradi. K е lgusida ikkita to’plamning d е kart ko’paytmasi ko’rinishida b е riladigan binar noravshan munosabatlarni ko’zdan k е chiramiz xolos. Bu to’plamlarni X va Y orqali b е lgilaymiz. U holda ~R noravshan munosabatning X×Y da b е rilishi uchun (x,y,μ~R(x,y)) uchta nuqta ko’rsatiladi, bu y е rda x∈X , y∈Y , yoki xuddi shunday (x,y)∈X×Y . 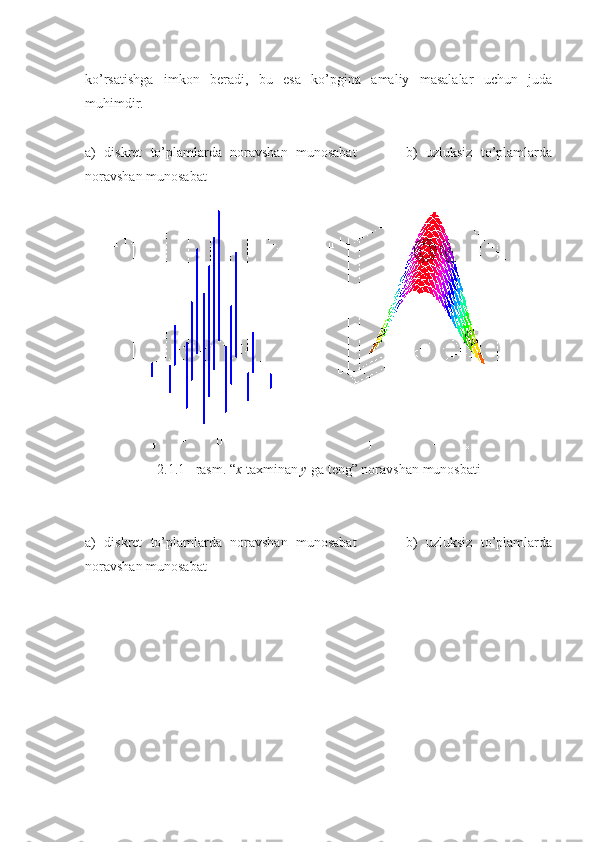x≈ y noravshan munosabat qo’yilsin ("x taxminan y" ga t е ng). x,y∈{0,1,2,3 } bo’lsin. U holda noravshan munosabatni quyidagi ko’rinishdagi matritsa bilan b е rish qulay: Uzluksiz to’plam X =[0,3] va Y =[0,3] lar uchun noravshan munosabatni μ~R(x,y)=e−0.2(x−y)2 tegishlilik funksiyasi yordamida berib qo’yish mumkin. x≈ y noravshan munosabatning diskret uzluksiz to’plamlarda berilish yo’llari 2.1.1- rasmda tasvirlangan. x,y∈{0,1,2,3 } bo’lsin. y dan ancha kichik bo’lgan x noravshan munosabatni matrisa ko’rinishida berib qo’yish mumkin: . Uzluksiz to’plamlar X =[0,3] va Y =[0,3] uchun " x munosabat y dan ancha kichik ekanligini quyidagi tegishlilik funksiyasi yordamida aniqlash mumkin: μ~ R (x,y)= ¿{0, agar x≥ y,¿¿¿¿ Diskret va uzluksiz to’plamlarda " x noravshan munosabat y dan kichik bo’lishi” 2.1.2- rasmda tasvirlangan. Bundan ko’rinib turganidek, noravshan munosabatlar an’anaviy munosabatlarga qaraganda anchagina egiluvchandir. Ular nafaqat munosabatlarning bajarilish omilini yaratishga, balki uning bajarilish darajasini ko’rsatishga imkon beradi, bu esa ko’pgina amaliy masalalar uchun juda muhimdir. a) diskret to’plamlarda noravshan munosabat b) uzluksiz to’plamlarda noravshan munosabat 2.1.1 –rasm. “ x taxminan y ga teng” noravshan munosbati a) diskret to’plamlarda noravshan munosabat b) uzluksiz to’plamlarda noravshan munosabat 2.1.2-rasm- « x y dan ancha kichkina » noravshan munosabati “O’xshash mentalitet” munosbatini quyidagi { O’zbekar (O’), Chexlar (Ch), Avstraliyaliklar (A), Nemislar (N)} millatlar uchun berish talab etilsin. Oddiy noravshan munosbatdan foydalanish o’xhash mentalitetli faqatgina bitta millatlar jufligi- nemis va avstraliyaliklarni ajratib ko’rsatishga imkon beradi. Bu munosbatlardan chexiyada mentalitet o’zbeklarga qaraganda nemislarnikiga yaqinroq ekanligi kelib chiqmaydi. Noravshan munosabat quyidagi axborotni osonlikcha taqdim etishga imkon beradi: O’ Ch A N . Noravshan ma’lumotning tashuvchisi. Noravshan ma’lumotning X va Y to’plamdagi tashuvchisi ~R deb ko’rinishdagi X×Y dekart ko’paytmaning qism to’plamiga aytiladi. Noravshan munosabat tashuvchisini noravshan munosabati deb ~R ning bajarilish darajasi nolga teng bo’lmagan barcha (x,y)∈X×Y juftliklarni bog’lovchi oddiy munosabat tushuniladi. Noravshan munosabatning α - kesimlaridan foydalanish maqsadga muvofiqroqdir, ularning ta’rifi α -darajali to’plamlarning ta’rifiga o’xshash. (1.2 bo’limga qarang). Noravshan ma’lumotning kesishmasi. Noravshan ma’lumotning X va Y to’plamdagi kesishmasi ~R deb (x,y)∈X×Y larni bog’lovchi oddiy munosabatga aytiladi, bu juftliklar uchun noravshan ~R munosabatning α dan kichik bo’lmagan bajarilish darajasi: ga teng. ~R norvashan munosbat X×X da refleksli deyiladi, agar ixtiyoriy x∈X uchun μ~R(x,x)=1 tenglik bajarilsa. Chekli X to’plam holida ~R matrisaning bosh diagonalidagi barcha elementlar 1 ga teng. Refleksli noravshan munosabatga misol sifatida “taxminan teng” munosbati olinishi mumkin. ~R norvashan munosbat X×X da antireffleksli deyiladi, agar ixtiyoriy x∈X uchun μ~R(x,x)=0 tenglik bajarilsa. Chekli to’plam holida ~R matrisaning bosh diagonalidagi barcha elemetlar 0 ga teng. Antirefleksli noravshan munosabatga misol tariqasida “ancha katta” munosabati keltirilishi mumkin. ~R noravshan munosabat X×Y da simmetrik deyiladi, agar har qanday (x,y)∈X×Y juftlik uchun μ~R(x,y)= μ~R(y,x) tenglik bajarilsa.Simmetrik noravshan munosabat chekli to’plamda berilsa, uning matrisasi ham simmetrikdir. ~R noravshan munosabat X×Y da assimmetrik deyiladi, agar μ~R(x,y)>0⇒ μ~R(y,x)= 0 munosabat har qanday (x,y)∈X×Y juftlik uchun o’rinli bo’lsa. Assimmetrik noravshan munosbatga “ancha katta” munosabati misol bo’lishi mumkin. ~R va ~R−1 noravshan munosbatlar X×Y da teskari deyiladi, agar ixtiyoriy (x,y)∈X×Y juftlik uchun μ~R(x,y)= μ~R−1(y,x) tenglik bajarilsa. Teskari noravshan munosbatga misol sifatida “ancha katta”- “ancha kichgina” juftligi xizmat qilishi mumkin. Foy dalanilgan adabiy ot lar 9. Muhamediyeva D.T. Noravshan axborot holatida sust shakllangan jarayonlarni modellashtirish. Toshkent: O’zR FA matematika va axborot texnologiyalar instituti, 2010. 37 ta jadval, 87 ta rasm, 155 ta bibl.atama, 400 bet. 10. Артикова С., Мухамедиева Д.Т. Информатизация регулирования развития экономики Республики // Известия ВУЗов. –Т., 2000. №3. 11. Артикова С., Мухамедиева Д.Т. Реализация моделей принятия решений с учетом информационых ситуаций //Узбекский журнал энергетики и информатики.-Т. ,2000. №3. 12. Ахмедов Т.М. Мухамедиева Д.Т. Шодмонова У.А. Рациональное управление распределением и использованием ресурсов в условиях рыночной экономики. Доклады международной конференции «Устойчивое экономическое развитие и эффективное управление ресурсами в Центральной Азии». ТГЭУ и Ноттенгемский Трент Университет (Великобритания). Ташкент-Ноттенгем. 2001. –С.14-17. Mavzu:Noravshan munosabt lar ust ida amallar Re ja K irish. 1. Noravshan munosbat ning t o'ldirmasi 2. Binar noravshan munosabat lar Foydalanilgan adabiyot Kirish. Noravshan munosbatlar o’rtasidagi amallar oddiy munosabatlarning amallariga o’xshashdir. Noravshan nazariy-to’plamli amallardek, ular turli xil usulda bajarilishi mumkin. Quyida uchburchak normalar, konormalarni qo’llovchi noravshan munosabatlar ustida olib boriladigan amallarga ta’rif keltiriladi (1.2- bo’limga qarang). Noravshan munosabatlarning kesishmasi . ~A va ~B noravshan munosabatlarning X×Y dagi kesishmasi deb μ~C(x,y)=t(μ~A(x,y),μ~B(x,y)) tegishlilik funksiyasi orqali berilgan ~C=~A∩ ~B noravshan munosabatga aytiladi, bu yerda (x,y)∈X×Y , t(⋅) - t-norma. N oravshan munosabatlarning umumlashmasi. ~A va ~B noravshan munosabatlarning X×Y dagi umumlashmasi deb μ~D(x,y)=s(μ~A(x,y),μ~B(x,y)) tegishlilik funksiyasi orqali berilgan ~D=~A∪~B noravshan munosbatga aytiladi, bunda (x,y)∈X×Y , s(⋅) - s -norma ( t -konorma). Noravshan munosbatlarning kesishmasi va umumlashmasi “ x taxminan y " ga teng va “ x ” “ y ” dan ancha kichkina noravshan munosabatlar ustida ko’rildi . t- norma va s-norma sifatida mos ravishda minimum va maksimumni topish amallari qo’llanildi. Noravshan munosabatlarning kesishmasi Noravshan munosabatlarning umumlashmasi 2.1.3-rasm - 2.1.1 va 2.1.2 rasmlarda berilgan noravshan munosabatlar ustida amallar Noravshan munosbatning to'ldirmasi. ~R noravshan munosbatning X×Y dagi to'ldirmasi deb tegishlilik funksiyasi μ~R'(x,y)=1− μ~R(x,y) bo’lgan ~R' noravshan munosbatga aytiladi, (x,y)∈X×Y . ~A va ~B noravshan munosabatlarning X×Z va Z×Y dagi maksimin kompozitsiyasi (ko’paytmasi) deb X×Y to’plamdagi μ~G(x,y)=sup z∈Z min (μ~A(x,z),μ~B(z,y)) tegishlilik funksiyali ~G=~A∘~B munosbatga aytiladi, bunda (x,y)∈X×Y , (x,z)∈X×Z , (z,y)∈Z×Y . X,Y,Z chekli ko’paytmalar holida ~G=~A∘~B noravshan munosabat matrisasi ~A va ~B larning maksimin ko’paytmasi ko’rinishida bo’ladi. Bu amal matrisalarni oddiy ko’paytirishdek bajariladi, bunda elementma-element ko’paytirish amali minimumni topish bilan, qo’shish esa - maksimumni topish bilan almashtirilgan. Huddi shu usulda minimaks va maksimultiplikativ kompozitsiyasi amallari aniqlanadi. Kompozitsiya noravshan mantiqiy chiqarishda kalit vazifasini o’taydi. M isol. Noravshan munosabatlar ~A=[ 0.1 0.2 0.8 1 ] va ~B=[ 0.6 0.4 0.5 0.3] berilgan. U holda bu noravshan munosabatlarning maksimaks (~G1) , minimaks (~G2) va maksimultiplikativ (~G3) kompozitsiyalari: ~G1=[ 0.1 0.1 0.5 0.3] ; ~G2=[ 0.5 0.3 0.8 0.8] ; ~G3=[ 0.1 0.06 0.5 0.32 ] matrisalar bilan tasvirlanadi. ~R noravshn munosabat X×Y da tranzitiv deyiladi, agar ~R∘~R⊆~R bo’lsa. Boshqa so’z bilan aytganda, har qanday (x,y)∈X×Y juftlik uchun ~R munosabatning bajarilish darajasi ~R∘~R ning bajarilish darajasidan kichik bo’lmasligi kerak. ~R ning tranzitiv tutashuvi ^R deb ^R= ~R∪~R2∪ ~R3∪ ...∪~Rn∪ ... munosabatga aytiladi, bu yerda ~Rn=~R∘~R∘...∘~R ⏟ nmarta . R noravshan munosabatning Xi1...Xik(i1,...,ik) dagi (1,2,…,n) ketma-ketlikka proyeksiyasi deb quyidagi ko’rinishda aniqlangan Xi1×...× Xik dagi munosabatga aytiladi: proj (R;Xi1,...,Xik)= ∫ Xi1×...×Xik sup Xj1,...,Xjk μR(X1,...,Xn)/(Xi1,...,Xik) , (2.1.1) bu yerda (j1,...,jk) - (1 ,…,n) da (i1,...,ik) gacha to’ldirilgan qism ketma- ketlik. Proyeksiyalar, shuningdek, marginal noravshan cheklanishlar deb ham ataladi. Aksincha, agar R - Xi1×...× Xik dagi noravshan to’plam bo’lsa, u holda X1×...×Xn dagi silindrik kengaytma - X1×...×Xn dagi C(R) noravshan to’plam bo’lib, u quyidagi munosabat orqali aniqlanadi: C(R)= ∫ X1×...×Xn μR(Xi1,...,Xik)/(X1,...,Xn) . n - tali noravshan chegaralanish R(v1,...,vn) bo’linuvchi deyiladi, faqat va faqat quyidagi shart bagarilsa: R(v1,...,vn)= R(v1)×...× R(vn) , bu yerda ¿ kartezian ko’paytmani va R(vi) - R ning X dagi proyeksiyasini ifodalaydi, ya’ni μR(X1,...,Xn)= min i=1,n μproj [R;Xj](Xi) . Silindrik kengaytmaning atamalarida bu formula quyidagi ko’rinishda qayta yozib olinishi mumkin: R=intersect i=1,n C(proj [R:Xi]) . R uning proyeksiyalari birlashmalari bo’lgandagina bo’linuvchidir. Agar R bo’linuvchi bo’lsa, u holda barcha marginal noravshan bo’linishlar ham bo’linuvchidir. v1,...,vn o’zgaruvchilar o’zaro ta’sirlashmaydigan deyiladi, agar ularning chegaralanishi R(v1,...,vn) bo’linuvchi noravshan munosabat bo’lsa. Misol. Agar A=0,1/4+0,3/5+0,4/6, B=0,33/10+0,45/11+0,78/12 bo’lsa, R= A× B noravshan munosabatni hisoblaymiz. min amalning o’rniga max va prod amallardan foydalanamiz. μR= max (μA,μB) . R= A× B = 0,33/(4.10)+0,45/(4.11)+0,78/(4.12)+0,33/(5.10)+ +0,45/(5.11)+0,78/(5.12)+0,4/(6.10)+0,45/(6.11)+0,78/(6,12). R=| 0,33 0,45 0,78 0,33 0,45 0,78 0,4 0,45 0,78 | μR=(μA× μB). R= A× B = 0,033/(4.10)+0,045/(4.11)+0,078/(4.12)+0,099/(5.10)+ +0,135/(5.11)+0,234/(5.12)+0,132/(6.10)+0,180/(6.11)+0,312/(6,12). R=| 0,033 0,045 0,078 0,099 0,135 0,234 0,132 0,180 0,312 | Binar norav shan munosabat lar Binar noravshan munosabatlar - bu klassik binar munosabatning umumlashmasidir. X×Y dagi R binar munosabat - bu X×Y dagi noravshan to’plamdir. R - X×Y dagi binar noravshan munosabat bo’lsin. R munosabatning domeni dom(R) va uning rangi ran(R) mos ravishda quyidagicha aniqlanadi: μdom (R)(x)= sup y μR(x,y),∀ x∈ X , μran (R)(y)= sup x μR(x,y),∀ y∈Y . Sup-Star kompozitsiya . Agar R va S U×V hamda V×W dagi noravshan munosabatlar bo’lsa, R va S kompozitsiya noravshan munosabat bo’lib, R∘S kabi belgilanadi hamda quyidagicha aniqlanadi: R∘S={[(x,y},sup y∈Y (μR(x,y)∗μS(y,z))]x∈X ,y∈Y,z∈Z¿¿ . (2.1.2) Bu yerda * - uchburchaksimon normalar sinfidagi ixtiyoriy operator, aniqrog’i: minimum, algebraik ko’paytma, chegaralangan ko’paytma yoki qat’iy (drastic) ko’paytma bo'lishi mumkin [35] . (2.1.2) tenglama quyidagi tarzda talqin etilishi mumkin: μR∘S(x,z) - X ni Z bilan ulovchi zanjirlar to’plamining kuchidir. Har bir zanjir x-y-z shaklga ega. Bunday zanjirning kuchi eng sust ulanishning kuchiga tengdir. X va Z o’rtasidagi munosabatning kuchi x va z o’rtasidagi eng kuchli ulanishning kuchidir. А – X dagi noravshan to’plam bo’lsin. (2.1.2) ni quyidagicha yozib olish mumkin: μA∘R(y)= sup x min (μA(x),μR(x,y)) . Biz B= A∘R ni A dan R orqali induksiyalangan noravshan to’plam deb ataymiz. Bu induksiya mashhur ravshan qoidani umumlashtiradi: agar х = а va y=f(x) bo’lsa, u holda y=f(a). B= proj [C (A)∩ R;Y ] ga ega bo’lamiz. Noravshan munosbatni chekli universumda tasvirlash mumkin. Bog’langan X va Y universumlar chekli bo’lsa, X∗Y dagi R noravshan munosabat [R] matrisa ko’rinishida tasvirlanishi mumkin, uning termi [R]ij μR(xi,yj)= rij, i= 1,n; j= 1,m ga teng bo’lib, bu yerda |X|=n |Y|=m . [S]jk= S jk , k= 1,p; P=|Z| ni hisobga olgan holda, chekli noravshan munosabatlarning kompozitsiyasi [ROS ]ik= ∑ j rijS jkmatrisaviy ko’paytma ko’rinishida qaralishi mumkin, bu yerda yig’indi max amali, ko’paytirish esa min amali orqali amalga oshiriladi. R∘S quyidagi ko’rinishda yozib olinganligi mumkin: proj [C (R)∩C (S);X× Z ] . Bu yerda R va S X×Y va Y×Z da berilgan bo’lib, boshqa kompozitsiyalar kesishmaga nisbatan qo’llanilgan operatorni zamonaviylashtirish orqali kiritilishi mumkin. min ni * ga o’zgartirib, R∗S ni μR∗S(x,z)= sup y (μR(x,y)∗ μS(y,z)) orqali kiritamiz. Biz boshqa ustuvor kompozitsiyalar inf-max, sup-prod va boshqalarga duch kelishimiz mumkin. 2.1.3. A gar-u holda norav shan munosabat А va В – X va Y unive rsumlardagi noravshan qism t o’plamlardir. A va B noravshan qism to’plamlarni X va Y mulohazalar sohasida bog’lash uchun, noravshan shartli tasdiq tushunchasi kiritiladi, ya’ni A→ B “Agar A u holda B” . Implikasiya orqali olingan R munosabat A va B qism to’plamlarning kartezian ko’paytma atamalarida ifodalanib, R= A× B orqali belgilanadi va uning tegishlilik funksiyasi quyidagicha aniqlanadi: μR(x,y)= μA×B(x,y)= min [μA(x),μB(y)],x∈ X ,y∈Y . (2.1.3) Foy dalanilgan adabiy ot lar 13. Muhamediyeva D.T. Noravshan axborot holatida sust shakllangan jarayonlarni modellashtirish. Toshkent: O’zR FA matematika va axborot texnologiyalar instituti, 2010. 37 ta jadval, 87 ta rasm, 155 ta bibl.atama, 400 bet. 14. Артикова С., Мухамедиева Д.Т. Информатизация регулирования развития экономики Республики // Известия ВУЗов. –Т., 2000. №3. 15. Артикова С., Мухамедиева Д.Т. Реализация моделей принятия решений с учетом информационых ситуаций //Узбекский журнал энергетики и информатики.-Т. ,2000. №3. 16. Ахмедов Т.М. Мухамедиева Д.Т. Шодмонова У.А. Рациональное управление распределением и использованием ресурсов в условиях рыночной экономики. Доклады международной конференции «Устойчивое экономическое развитие и эффективное управление ресурсами в Центральной Азии». ТГЭУ и Ноттенгемский Трент Университет (Великобритания). Ташкент-Ноттенгем. 2001. –С.14-17.

Mav zu:Norav shan t o’plamlarning asosiy t ushunchalari v a t arifl ari Reja: Kirish 1. Norav shan t o’plamlar nazariy asi 2. Asosiy at ama v a t ushunchalar 3. Norav shan t o’plam t ushunchasi Foy dalanilgan adabiy ot lar

KIRISH Hozirgi vaqtda haqiqiy jarayonlarni mod е llashtirish va muqobillashtirishda noaniqliklarni hisobga olish zaruriyati h е ch kimda shubha tug’dirmay qo’ydi. Ayni vaqtda noaniqlikni qo’llashga doir klassik nazariy-ehtimollik yondashuvning ch е klanishlarini anglash oxirgi uchta o’n yillik ichida ko’p sonli ustvor nazariyalar va usullarning paydo bo’lishiga olib k е ldi. Ulardan noravshan to’plamlar nazariyasini, uning asosida qurilgan imkoniyatlar nazariyasi va noravshan mantiqni, amaliy int е rval tahlil, taqribiy to’plamlar nazariyasini ajratib ko’rsatish mumkin. Ushbu asosiy nazariyalarning ko’pgina zamonaviy ko’rinishlari, shu jumladan r е lyativistik va kvant nazariyalari, noravshan to’plamlarning intuitiv nazariyasi va h.k.lar mavjud. Jumladan yangi yondashuvlar klassik nazariyaviy- ehtimolli uslubiyatni rad etmasdan, aksincha usullarni to’g’ri birlashtirish yo’li bilan amaliy muammolarni anchagina samarali y е chishga imkoniyat yaratgan holda uni to’ldiradilar va k е ngaytiradilar. Noravshan to’plamlar nazariyasi (Fuzzy sets theory)ga 1965 yilda B е rkli Univ е rsit е ti prof е ssori Lotfi Zad е (Lotfi Zadeh) “Information and Control” jurnalida “Fuzzy sets” ishini chop etish orqali asos soldi. “Fuzzy” aniqlovchisi o’zb е k tiliga noravshan, noaniq, noqat'iy kabi tarjima qilinib, yangi nazariya «t е gishli-t е gishli emas», «rost-yolg’on» [35, 36, 37] aniq tushunchalar bilan ish yurituvchi an'anaviy klassik mat е matika va Aristot е l mantig’ini to’ldirish maqsadida kiritilgan. Noravshan to’plam kons е psiyasi, Zad е ning fikricha, haqiqiy dunyoning tizimlarida, ayniqsa odamlarni o’z ichiga olgan gumanistik tizimlarda noo’rin sun'iy aniqlikka erishishni talab qilgan tizimlarning klassik nazariyasiga oid mat е matik usullardan qoniqmaslik [35] hisobiga tug’ilgan. Noravshan to’plamlar nazariyasi 1975 yilda amaliyotda qo’llanilgan bo’lib, bunda Mamdani va Assilian (Mamdani and Assilian)lar oddiy bug’ dvigat е lini boshqarish maqsadida birinchi noravshan hisoblagichni qurganlar [101,129].

1982 yili Xolmblad va Ostergad (Holmbland and Osregaad) birinchi sanoatga oid noravshan hisoblagichni ishlab chiqishgan bo’lib, u Daniyadagi zavodlarning boshqaruvlaridan birida qo’llanilgan. “Agar-u holda” noravshan lingvistik qoidalarga asoslangan birinchi sanoat hisoblagichining muvaffaqiyati matematiklar va injenerlar o’rtasida noravshan to’plamlar nazariyasiga katta qiziqish uyg’otdi. Bir oz vaqtdan so’ng Bart Kosko (Bart Kosko) tomonidan noravshan approksimasiya teoremasi (Fuzzy Approximation Theorem) isbotlangan bo’lib, unga ko’ra har qanday matematik tizim noravshan mantiqqa asoslangan tizim orqali approksimatsiyalanishi mumkin. Boshqa so ’ z bilan aytganda , tabiiy tildagi “ Agar - u holda ” ko ’ rinishidagi mulohazalar - qoidalar , ularning noravshan to ’ plamlar nazariyasi vositalari yordamida kelgusidagi bayonoti yordamida boshqaruv va identifikatsiyalarda qo ’ llanilgan an ’ anaviy differensial va integral hisoblashlarning murakkab apparatidan foydalanmasdan turib , ixtiyoriy “ kirishlar - chiqish ” bog ’ lanishni xohlaganchalik darajada aniq akslantirish mumkin . Noravshan to ’ plamlarga asoslangan tizimlar texnologik jarayonlarni boshqarish , transportni boshqarish , tibbiy tashxis , texnik tashxis , moliyaviy menejment , birjaviy bashorat , tasvirlarni aniqlash kabi sohalarda ishlab chiqilgan va qo ’ llanilgan . Noravshan mantiqiy chiqarish tizimlarini ishlab chiqishga oid amaliy tajriba ularni loyihalashtirishga ketgan vaqt va xarajatlar an ’ anaviy matematik apparatdan foydalanishga nisbatan ancha kam ekanligi to ’ g ’ risida dalolat beradi , jumladan bunda modellarning zaruriy darajadagi ishchanligiga va shaffofligiga erishiladi . Taqdim etilayotgan ish statistik modellardagi noaniq kattaliklarga ( oraliqli , noravshan va h . k ) asoslangan holda amaliyotda hisoblashlar olib borish masalalariga bag ’ ishlanadi . Asosiy e’tibor modellashtirish, murakkab tizimlarning ishlashini muqobillashtirish va sifatini baholash uchun noravshan to’plamlar va interval tahlil nazariyalarining amaliy ilovalariga qaratilgan. Noravshan to’plamlar nazariyasining asosiy atamalari va tushunchalari bayon etilgan. Asosiy atama va tushunchalar

Vaqtning haqiqiy masshtabida masalalarni yechishning xususiyatlari shuni ko’rsatadiki, hisoblash imkoniyatlarining yetishmovchiligi masalaning sharoitlari to’g’risidagi axborotning yetishmasligiga ekvivalent bo’lishiga olib keladi. Universal to’plam bittadan ortiq nuqtaga ega bo’lgandagina [44] ishga ko’ra noaniqlik o’rinlidir. Agar to’plamning ushbu elementlari uchun mos ehtimollar yoki boshqa ehtimolli tavsiflar berilgan bo’lsa, u holda ehtimolli noaniqlik o’rinlidir. Agar to’plamning faqatgina chegeraviy elementlari ma’lum bo’lsa - interval noaniqlik o’rinlidir. Va nihoyat, to’plamning har bir elementi uchun tegishlilik darajasi berilgan bo’lsa - noravshanlik ko’rinishidagi noaniqlik o’rinlidir. Noravshan to’plam tushunchasi - matematik modellarni qurish uchun noravshan ma’lumotni matematik jihatdan bayon etishga harakat qilingan urinishlardir. Ushbu tushunchaning zaminida berilgan to’plamni tashkil qilgan bir xil xususiyatli elementlar shu xususiyatga har xil darajada ega bo’lishi, demak berilgan to’plamga har xil darajada tegishli bo’lishi mumkinligi to’g’risidagi tasavvur yotadi. Bunday yondashuvga asosan “qandaydir element berilgan to’plamga tegishli” ko’rinishidagi mulohazalar ma’noga ega bo’lmay qoladi, chunki aniq bir element berilgan to’plamni qanday darajada yoki “qanchalik kuchli” qoniqtirishini ko’rsatish zarur [35]. U tashuvchi- bu baholanayotgan kvazistatistika doirasidagi kuzatishlarning barcha natijalari tegishli bo’lgan universal to’plamdir. Masalan, agar biz paxtaning hosildorligini kuzatayotgan bo’lsak, u holda tashuvchi - o’lchov birligi senter bo’lgan bir gektardan olinadigan paxta miqdori qo’yilgan haqiqiy o’qdan ajratilgan kesmadir. U universal top’lamdagi ~A noravshan to’plam (fuzzy set) deb ( μ~A,u ) juftliklar majmuiga aytiladi, bunda μ~A - elementning ~A noravshan to’plamga tegishlilik darajasidir. Tegishlilik darajasi - [0, 1] oraliqdagi sondir. Tegishlilik

darajasi qanchalik yuqori bo’lsa, universal to’plamning elementi [116,126,152] noravshan to’plamning xossalariga shunchalik ko’proq darajada tegishli bo’ladi. А noravshan to ’ plam – tashuvchining har bir qiymatiga ushbu qiymatning A to ’ plamga tegishlilik darajasi mos qo ’ yilgan tashuvchining qiymatlar to ’ plamidir [107,128]. Masalan : lotin alifbodagi X , Y , Z harflar , albatta , Alphabet = { A , B , C , X , Y , Z } to ’ plamga tegishli va shu nuqtai nazardan Alphabet – ravshan . Lekin “ Paxtaning muqobil hosildorligi ” to ’ plamini tahlil qiladigan bo ’ lsak , u holda 50 s / ga hosildorlik berilgan noravshan to ’ plamga ma ’ lum  darajada tegishli bo ’ lib , uni tegishlilik funksiyasi deb ataydilar . Tegishlilik funksiyasi (membership function) - bu universal to ’ plamdagi ixtiyoriy elementning noravshan to ’ plamga tegishlilik darajasini hisoblashga imkon beruvchi funksiyadir . Agar universal to’plam U ={u1,u2,...,uk} chekli sondagi elementlardan iborat bo’lsa, u holda ~A noravshan to’plam ~A= ∑ j=1 k μ~A(uj)/uj ko’rinishida yoziladi. Uzluksiz U to’plam holida ~A= ∫ [u,u] μ~A(u)/u belgilashdan foydalanishga kelishilgan. Masalan, “paxtaning o’rtacha hosildorligi” tushunchasini noravshan to’plam ko’rinishida quyidagicha tasvirlash mumkin: ~ A = 0/21+0.1/22 + 0.3/23 + 0.8/24 +1/25 +1/26 + 0.5/27 +0/28. 1.1.1-rasmda “Paxtaning hosildorligi” noravshan to’plamining bir qator mutaxassislar o’rtasida so’rov o’tkazish orqali hosil qilingan tegishlilik funksiyasi keltirilgan.

O'xshashlar

Noravshan to’plamlarning asosiy tushunchalari va tariflari
Noravshan to’plamlarning arifmetikasi
Ijodkorlik faoliyatining asosiy tushunchalari.
Axborot texnologiyalarining asosiy tushunchalari
Axborot texnologiyalarining asosiy tushunchalari.