Taqribiy sonlar. Ularning absolyut va nisbiy xatosi. Qiymatga ega bo’lgan raqam. To’g’ri ishoralar soni doc




![x
n + 1 = x
n − f( x
n )
f
( a ) − f ( x
n ) ∗ ( a − x
n ) = 1,2
x≈0,79
Nyuton usuli
[
a , b ] = [ 1,2 ]
a + b
2 = 1,5
f(a)∗ f(c)<0f(1)∗ f(1,5 )<0
f
( b) ∗ f ( c) < 0 f ( 2 ) ∗ f ( 1,5 ) < 0
f(1)=-2
f(2)=8
f(3/2)=2,6
Chiziqli algebraik tenglamalar sistemasini (ChATS) yechishning sonli
usullari. Gauss, oddiy iteratsiyalar, Zeydel usullari
1. Biz tenglamalarni matritsa ko'rinishida yozamiz:
1.7 10 -1.3 2.1 | 3.1
3.1 1.7 -2.1 5.4 | 2.1
3.3 -7.7 4.4 -5.1 | 1.9
10 -20.1 20.4 1.7 | 1.8
2. Birinchi qattni ikkinchi qatrga 1.7 va uchinchi qatrga 3.3 qo'shib qo'yamiz:
1.7 10 -1.3 2.1 | 3.1
0 -15.3 -6 0.95 | -3.9
0 25.78 7.33 -11.82| -7.07
10 -20.1 20.4 1.7 | 1.8
3. Ikkinchi qattni uchinchi qatrga 25.78 bo'lib 10 qo'shib qo'yamiz:
1.7 10 -1.3 2.1 | 3.1
0 -15.3 -6 0.95 | -3.9
0 0 160.39 -122.85 | -49.89
10 -20.1 20.4 1.7 | 1.8
4. Keyingi qobriqni 160.39 ga bo'lip birinchi va uchinchi qatrlarga ko'paytiramiz:
1.7 10 -1.3 2.1 | 3.1
0 -15.3 -6 0.95 | -3.9
0 0 160.39 -122.85 | -49.89
0 -37.91 115.75 -19.77 | -29.33
5. Oxirgi qatrdan birinchi va uchinchi qatrlarni 115.75 ga bo'lib ko'paytiramiz:](/data/documents/19a16c91-410b-4db3-9213-abc878a8125c/page_6.png)
![1.7 10 -1.3 2.1 | 3.1
0 -15.3 -6 0.95 | -3.9
0 0 160.39 -122.85 | -49.89
0 0 118.18 -33.74 | -16.92
6. Bizning yechimiz:
x = 0.25
y = 0.254902
z = -0.306122
d = -0.122449
Gaus usuli
import numpy as np
def gauss_elimination(A, B):
n = len(B)
for i in range(n):
max_index = i
max_value = abs(A[i][i])
for j in range(i+1, n):
if abs(A[j][i]) > max_value:
max_index = j
max_value = abs(A[j][i])
A[[i, max_index]] = A[[max_index, i]]
B[[i, max_index]] = B[[max_index, i]]
for j in range(i+1, n):
factor = A[j][i] / A[i][i]
B[j] -= factor * B[i]
A[j] -= factor * A[i]
X = np.zeros(n)
for i in range(n-1, -1, -1):
X[i] = (B[i] - np.dot(A[i,i+1:], X[i+1:])) / A[i][i]
return X
A = np.array([[2.0, 1.0], [5.0, 3.0]])
B = np.array([4.0, 10.0])
X = gauss_elimination(A, B)
print("Natija:")
print(X)
Zeydel usuli
import numpy as np
def zeydel_usuli(A, b, x0, eps=1e-5, max_iter=1000):
n = len(b)
x = np.copy(x0)
x_new = np.copy(x)
for _ in range(max_iter):
for i in range(n):](/data/documents/19a16c91-410b-4db3-9213-abc878a8125c/page_7.png)
![x_new[i] = b[i]
for j in range(n):
if j != i:
x_new[i] -= A[i, j] * x_new[j]
x_new[i] /= A[i, i]
if np.linalg.norm(x_new - x) < eps:
return x_new
x = np.copy(x_new)
return x
A = np.array([[10, 2, 1], [1, 5, 1], [2, 3, 10]])
b = np.array([7, -8, 6])
x0 = np.array([0, 0, 0])
print("Zeydel usuli:")
print(zeydel_usuli(A, b, x0))
x = (3.1 - 10*y + 1.3*z - 2.1*d)
y = (2.1 - 3.1*x + 2.1*z - 5.4*d)
z = (1.9 - 3.3*x + 5.1*d)
d = (1.8 - 10*x - 20.1*d)
k x
1 (k)
x
2 (k)
x
3 (k)
x
4 (k)
0.3,1 2,1 1,9 1,8
…… ……. ………. ……
…… ……. …… ……. ……
import numpy as np
def chiziqli_ustun(A, b, eps=1e-5, max_iter=1000):
n = len(b)
x = np.zeros(n)
for _ in range(max_iter):
x_new = np.copy(x)
for i in range(n):
x_new[i] = (b[i] - np.dot(A[i, :i], x_new[:i]) - np.dot(A[i, i+1:], x[i+1:])) /
A[i, i]
if np.linalg.norm(x_new - x) < eps:
return x_new
x = x_new
return x
A = np.array([[10, 2, 1], [1, 5, 1], [2, 3, 10]])
b = np.array([7, -8, 6])
print("Chiziqli ustunlar:")
print(chiziqli_ustun(A, b))](/data/documents/19a16c91-410b-4db3-9213-abc878a8125c/page_8.png)
![Nochiziqli tenglamalar sistamasini yechish usullari. Oddiy iteratsiyalari,
Nyuton usullari.
Oddiy iteratisya usuli
x = 0
y = 0
1. x(n+1) = - sin(y(n)) - 0.4
2. y(n+1) = cos(x(n)+1) / 2
x(1) = -sin(0) - 0.4 = -0.4
y(1) = cos(1)/2 ≈ 0.417
import numpy as np
def oddiy_iteratsiyalar(A, b, x0, eps=1e-5, max_iter=1000):
n = len(b)
x = np.copy(x0)
for _ in range(max_iter):
x_new = np.zeros(n)
for i in range(n):
x_new[i] = b[i]
for j in range(n):
if j != i:
x_new[i] -= A[i, j] * x[j]
x_new[i] /= A[i, i]
if np.linalg.norm(x_new - x) < eps:
return x_new
x = x_new
return x
A = np.array([[10, 2, 1], [1, 5, 1], [2, 3, 10]])
b = np.array([7, -8, 6])
x0 = np.array([0, 0, 0])
print("Oddiy iteratsiyalar usuli:")
print(oddiy_iteratsiyalar(A, b, x0))
Nyuton usuli
x=-0,8 y=0,4
f(x,y) = 2*y - cos(x+1) - 0
g(x,y) = x + sin(y) + 0.4](/data/documents/19a16c91-410b-4db3-9213-abc878a8125c/page_9.png)
![FI(x,y)= cos (x+1)
2G I
(
x , y ) = arcsin ( − x − 0.4 )
F I
(
x , y ) = − cos ( y + 1 )
2
G
( x , y ) = − sin ( y ) − 0.4
J
( x , y ) =
| cos
( x + 1 )
2
− cos
( y + 1 )
2 arcsin ( − x − 0.4 )
− sin ( y ) − 0.4 | = − 0,45
import numpy as np
def f(x):
return np.array([
x[0]**2 + x[1]**2 + x[2]**2 - 2*x[0] - 3*x[1] + x[2] + 6,
x[0]**2 + 4*x[1]**2 + x[2]**2 - 3*x[0] - x[1] + 2*x[2] - 7,
x[0]**2 + x[1]**2 + 9*x[2]**2 + x[0] - x[2] + 6
])
def df(x):
return np.array([
[2*x[0] - 2, 2*x[1] - 3, 2*x[2] + 1],
[2*x[0] - 3, 8*x[1] - 1, 2*x[2] + 2],
[2*x[0] + 1, 2*x[1], 18*x[2] - 1]
])
def newton_method(f, df, x0, eps=1e-5, max_iter=1000):
x = np.copy(x0)
for _ in range(max_iter):
delta_x = np.linalg.solve(df(x), -f(x))
x = x + delta_x
if np.linalg.norm(delta_x) < eps:
return x
return x
x0 = np.array([0, 0, 0])
solution = newton_method(f, df, x0)
print("Nyuton usuli:")
print(solution)
MATRISANING XOS SON VA XOS VEKTORI MASALASI.
DANILEVSKIY VA KRILOV USULLARI
Danilevskiy usuli
(
1 2 3
7 − 1 5
2 3 − 3 ) = ¿
m
( x ) = det ( A − αl )](/data/documents/19a16c91-410b-4db3-9213-abc878a8125c/page_10.png)
![m(x)= det (
1− x 2 3
7 1− x 5
2 3 3− x)=¿m
( x ) = ( − 1 ) 3
∗ ( 1 − x ) ∗ ( − x 2
+ 4 ∗ x − 8 ) − 2 ∗ ( 7 ∗ ( − 3 − x ) − 5 ∗ 2 ) + 3 ∗ ( 7 ∗ 3 − 5 ∗ 2 ) = − x 3
+ 6 x 2
− 5 x + 33
m(x)=− 2x2+10 x+87
m(0)=−2(0)2+10 (0)+87 =87
m ( 1 ) = − 2
( 1) 2
+ 10 ( 1 ) + 87 = − 2 + 10 + 87 = 95
m(2)=−2(2)2+10 (2)+87 =−8+20 +87 =99
import numpy as np
def danilevsky_method(A):
n = A.shape[0]
P = np.eye(n)
for k in range(n-1, 0, -1):
v = np.zeros(n)
v[k] = 1
for j in range(k-1, -1, -1):
mu = A[j, k] / A[k, k]
v[j] = -mu
A[j, :] = A[j, :] + mu * A[k, :]
P_k = np.eye(n) - np.outer(v, P[:, k])
P = np.dot(P_k, P)
return P, A
# Matrisni yaratish
A = np.array([
[1, 2, 3],
[2, 5, 4],
[3, 4, 11]
])
P, B = danilevsky_method(A)
print("P:")
print(P)
print("Danilevski usuli:")
print(B)
Krilov usuli
(
1 2 3
7 − 1 5
2 3 − 3 ) = ¿
X 1 = A ∗ X 0 = A ∗ ( 1 , 1 , 1 )
¿ ( 1 ∗ 1 + 2 ∗ 1 + 3 ∗ 1 , 7 ∗ 1 + ( − 1 ) ∗ 1 + 5 ∗ 1 , 2 ∗ 1 + 3 ∗ 1 + ( − 3 ) ∗ 1 ) = ( 1 + 2 + 3 , 7 − 1 + 5 , 2 + 3 − 3 ) = ( 6 , 11 , 2 )
import numpy as np
def krilov_method(A, b):
n = A.shape[0]
x = np.zeros(n)
x[0] = 1
for i in range(1, n):](/data/documents/19a16c91-410b-4db3-9213-abc878a8125c/page_11.png)
![x = np.dot(A, x)
x = x / np.linalg.norm(x)
phi = np.dot(A, x)
lambd = np.dot(x, phi)
return lambd, x
# Matris va b vektorini yaratish
A = np.array([[2, -1], [1, 3]])
b = np.array([1, 4])
lambd, x = krilov_method(A, b)
print("Xalqalar son: ", lambd)
print("Xalqalar vektori: ", x)
FUNKSIYALARNI INTERPOLYASIYALASH. LAGRANJ va Nyuton
INTERPOLYASION FORMULASI
Lagranj usuli
Teng uzoklikda joylashmagan tugunlarda y funksiyaning qiymatlari berilgan.
Lagranj interpolyasion formulalari yordamida ko’phad quring va х nuqtadagi
qiymatini hisoblang.
X Y № x
0,02 1,02316
2 0,102
0,08 1,09590
4 0,114
0,12 1,14725
6 0,125
0,17 1,21483
8 0,203
0,23 1,30120
10 0,154
0,30 1,40976
12 0,087
L
5 (x)=( x − x
1 )( x − x
2 )( x − x
3 )( x − x
4 )( x − x
5 )
(
x
0 − x
1 )( x
0 − x
2 )( x
0 − x
3 )( x
0 − x
4 )( x
0 − x
5 ) y
0 + +
( x − x
0 )( x − x
1 )( x − x
2 )( x − x
3 )( x − x
4 )
(
x
1 − x
0 )( x
1 − x
2 )( x
1 − x
3 )( x
1 − x
4 )( x
1 − x
5 ) y
1
+
+(x− x1)(x− x0)(x− x3)(x− x4)(x− x5)
(x2− x1)(x2− x0)(x2− x3)(x2− x4)(x2− x5)
y2
+
+(x− x1)(x− x2)(x− x0)(x− x4)(x− x5)
(x3− x1)(x3− x2)(x3− x0)(x3− x4)(x3− x5)
y3
+
+
( x − x
1 )( x − x
2 )( x − x
3 )( x − x
0 )( x − x
5 )
(
x
4 − x
1 )( x
4 − x
2 )( x
4 − x
3 )( x
4 − x
0 )( x
4 − x
5 ) y
4 +
+
( x − x
1 )( x − x
2 )( x − x
3 )( x − x
4 )( x − x
0 )
(
x
5 − x
1 )( x
5 − x
2 )( x
5 − x
3 )( x
5 − x
4 )( x
5 − x
0 ) y
5
import numpy as np
def lagrange_interpolation(x, y, x_eval):
result = 0
for i in range(len(y)):](/data/documents/19a16c91-410b-4db3-9213-abc878a8125c/page_12.png)
![term = y[i]
for j in range(len(x)):
if j != i:
term = term * (x_eval - x[j]) / (x[i] - x[j])
result += term
return result
# Input ma'lumotlarni yaratish
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 5, 7, 11])
# Interpolatsiya uchun qiymatni hisoblash
x_eval = 3.5
result = lagrange_interpolation(x, y, x_eval)
print("Interpolatsiyalangan qiymat: ", result)
Nyuton usuli
Teng uzoklikda joylashgan tugunlarda y funksiyaning qiymatlari berilgan.
Nyutonning birinchi va ikkinchi interpolyasion formulalari yordamida ko’phad
quring va х nuqtadagi qiymatini hisoblang.
I X Y
Δ y
❑Δ1y❑ Δ2y❑ Δ3y❑ Δ4y❑
0 0,115 8,65729 -0,36 0,021 0,00864 -0,0155 -0,1437
1 0,120 8,29729 -0,339 0,02964 -0,00686 -0,01592
2 0,125 7,95829 -0,30936 0,02278 -0,02278
3 0,130 7,64893 -0,28658 0,02036
4 0,135 7,36235 -0,26622
5 0,140 7,09613
N
5 (x)=8,65729+
− 0,36
1 ! ∙ 0,005
( x − 0,115 ) + 0,021
2 ! ∙ 0,005 ( x − 0,115 )( x − 0,120 ) + 0,00864
3 ! ∙ 0,005 ( x − 0,115 )( x − 0,120 )( x − 0,125 ) + − 0,0155
4 ! ∙ 0,005 ( x − 0,115 )( x − 0,120 )( x − 0,125 )( x − 0,130 ) + − 0,1437
5 ! ∙ 0,005 ( x − 0,115 )( x − 0,120 )( x − 0,125 )( x − 0,135 ) = ¿
16.96568846-72,47830871x+1,962718117x 2
+0,4698441667x 3
-0,3686666667x 4
x=0,1315 dagi qiymatini hisoblaymiz
16.96568846-72,47830871x+1,962718117x 2
+0,4698441667x 3
-0,3686666667x 4
= >
Javob:7,47](/data/documents/19a16c91-410b-4db3-9213-abc878a8125c/page_13.png)


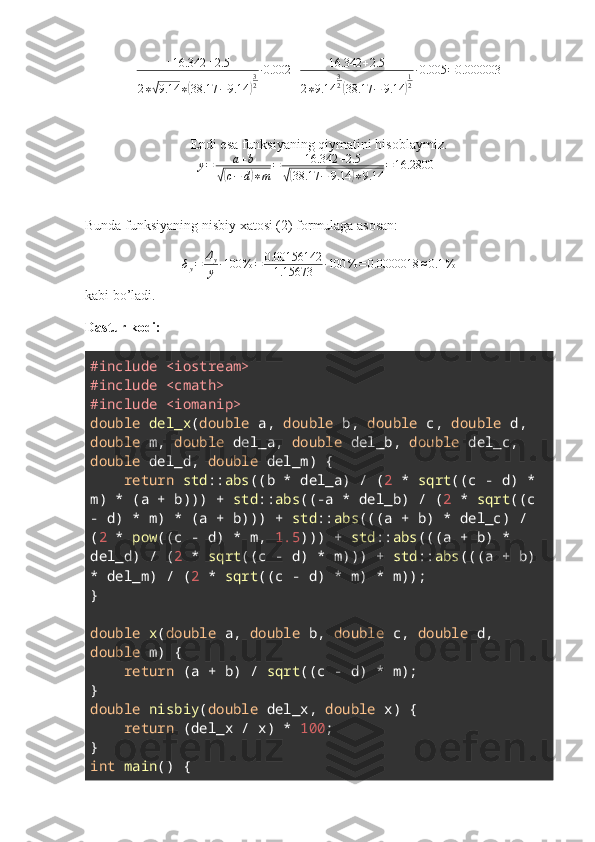
1-LABORATORIYA ISHI Mavzu: Taqribiy sonlar. Ularning absolyut va nisbiy xatosi. Qiymatga ega bo’lgan raqam. To’g’ri ishoralar soni . Differensiallanadigan funksiyaning y = f ( x 1 , x 2 … , x n ) absolyut xatosi argumentlarning x1,x2… ,xn deyarli kichik xato bilan chiqariladigan Δ x 1 , Δ x 2 , … Δ x n o’cham bilan baholanadi. ∆ y = ∑ i = 1n ❑ | ∂ f ∂ x i | ⋅ Δ x i (1) Bundan funksiyaning nisbiy xatosi δ y = Δ y y ∗ 100 % ( 2 ) kabi bo’ladi. Masalaning qo’yilishi: Quyidagi funksiyaning absolyut va nisbiy xatoligini aniqlang. y= a+b √(c− d)∗m a=16.342 ±0.0001 ;b= 2.5 ±0,003 ; c= 38.17 ±0,002 d=9.14 ±0,005 n=3.6 ±0,04 m= 9.14 ±0,04 Yechish: Demak: a=16.342 ;b= 2.5 ;c=38.17 ;d=9.14 ;n=3.6 ;m=9.14 ∆ a = 0.001 ; ∆ b = 0.003 ; ∆ c = 0.002 ∆ d = 0.002 ∆ n = 0.04 ∆ m = 0.005 (1) formulaga asosan funksiyaning absolyut xatosini topamiz. ∆ y = ∂ y ∂ a ⋅ Δ a + ∂ y ∂ b ⋅ Δ b + ∂ y ∂ c ⋅ Δ c + ∂ y ∂ d ⋅ Δ d + ∂ y ∂ m ⋅ m = ¿ 1 √( 38.17 − 9.14 ) ∗ 9.14 0.001 + 1 √( 38.17 − 9.14 ) ∗ 9.14 0.003 − 16.342 + 2.5 2 ∗ √ 9.14 ∗ ( 38.17 − 9.14 ) 3 2 ∙ 0.002
+ 16.342 + 2.5 2 ∗√ 9.14 ∗ ( 38.17 − 9.14 ) 3 2 ∙ 0.002 + 16.342 + 2.5 2 ∗ 9.14 3 2 ( 38.17 − 9.14 ) 1 2 ∙ 0.005 = 0.000003 Endi esa funksiyaning qiymatini hisoblaymiz. y= a+b √(c− d)∗m = 16.342 +2.5 √(38.17 − 9.14 )∗9.14 =16.28004 Bunda funksiyaning nisbiy xatosi (2) formulaga asosan: δ y = Δ y y ∙ 100 % = 0.00156142 1.15673 ∙ 100 % = 0.0000018 ≈ 0.1 % kabi bo’ladi. Dastur kodi: #include <iostream> #include <cmath> #include <iomanip> double del_x ( double a, double b, double c, double d, double m, double del_a, double del_b, double del_c, double del_d, double del_m) { return std :: abs ((b * del_a) / ( 2 * sqrt ((c - d) * m) * (a + b))) + std :: abs ((-a * del_b) / ( 2 * sqrt ((c - d) * m) * (a + b))) + std :: abs (((a + b) * del_c) / ( 2 * pow ((c - d) * m, 1.5 ))) + std :: abs (((a + b) * del_d) / ( 2 * sqrt ((c - d) * m))) + std :: abs (((a + b) * del_m) / ( 2 * sqrt ((c - d) * m) * m)); } double x ( double a, double b, double c, double d, double m) { return (a + b) / sqrt ((c - d) * m); } double nisbiy ( double del_x, double x) { return (del_x / x) * 100 ; } int main () {
double a = 16.342 ; double b = 2.5 ; double c = 38.17 ; double d = 9.14 ; double m = 9.14 ; double del_a = 0.001 ; double del_b = 0.003 ; double del_c = 0.002 ; double del_d = 0.002 ; double del_m = 0.005 ; double absolut_xato = del_x(a, b, c, d, m, del_a, del_b, del_c, del_d, del_m); double funksiya_qiymati = x(a, b, c, d, m); double nisbiy_xato = nisbiy(absolut_xato, funksiya_qiymati); std :: cout << "Funksiyaning qiymati: " << funksiya_qiymati << std :: endl ; std :: cout << "Absolut xatolik: " << absolut_xato << std :: endl ; std :: cout << "Nisbiy xatolik: " << std ::fixed << std ::setprecision( 1 ) << nisbiy_xato << " %" << std :: endl ; return 0 ; } Dastur natijasi: Chiziqlimas tenglamalarni yechishning sonli usullari. Nyuton, oddiy iteratsiya, vatarlar usullari. Nyuton usuli
def f(x): return x**2 - 4 def f_prime(x): h = 1e-6 return (f(x + h) - f(x)) / h def newton_method(f, f_prime, x0, tol=1e-6, max_iter=100): x = x0 for i in range(max_iter): fx = f(x) if abs(fx) < tol: break fp = f_prime(x) if fp == 0: break x = x - fx / fp return x x0 = 2.0 root = newton_method(f, f_prime, x0) print("Natija:", root) Vatarlar usuli # Sonli usul def sonli_usul(n): if n == 0: return 1 else: return n * sonli_usul(n-1) # Vatarlar usuli def vatarlar_usuli(n): result = 1 for i in range(1, n+1): result *= i return result n = int(input("Ixtiyoriy son kiriting: ")) print(f"{n} ning sonli usuli: {sonli_usul(n)}") print(f"{n} ning vatarlar usuli: {vatarlar_usuli(n)}") Oddiy iteratisiya usuli def iteratsiya_method(a, b, c): epsilon = 0.0001 x0 = 0 while True: x1 = (b * x0**2 + c) / a if abs(x1 - x0) < epsilon: break x0 = x1 print("Iteratsiya usuli natijasi:", x1)
a = float(input("a ni kiriting: ")) b = float(input("b ni kiriting: ")) c = float(input("c ni kiriting: ") iteratsiya_method(a, b, c) Oddiy itereatsiya usuli x 3 − 3 x 2 + 12 x − 12 = 0 f 1( x ) = x 3 − 3 x 2 f2(x)=12 x− 12 x -1 0 1 y -28 -12 -2 x0≤12 x n + 1 = x n − f ( x n ) f I ( x n ) f I ( x 0 ) = 3 x 2 − 6 x + 12 x1= x0− f(x0) fI(x0) ≈7,5 x2= x1− f(x1) fI(x1) ≈6,3 | x n − x n − 1 ≤ ε ε ≤ 10 − 4 | x ≈ 1,22 Vatar usuli f ( a) < 0 x n + 1 = x n − f ( x n ) f ( b ) − f ( x n ) ∗ ( b − x n ) f ( a) = − 12 f ( x 1 ) = − 12 − − 2316 − 4632 ∗ ( − 12 − 12 ) = − 1,99x -1 0 1 2 f1(x) -4 0 -2 -4 f 2 ( x ) -24 -12 0 12
